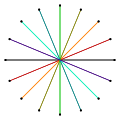
Hexadecagon

Regular hexadecagon
Regular hexadecagon
	A regular hexadecagon
Type	Regular polygon
Edgesandvertices	16
Schläfli symbol	{16}, t{8}, tt{4}
Coxeter–Dynkin diagrams	;
Symmetry group	Dihedral(D16), order 2×16
Internal angle(degrees)	157.5°
Properties	Convex,cyclic,equilateral,isogonal,isotoxal
Dual polygon	Self

In mathematics, ahexadecagon(sometimes called ahexakaidecagonor16-gon) is a sixteen-sidedpolygon.^[1]

Regular hexadecagon[edit]

Aregularhexadecagonis a hexadecagon in which all angles are equal and all sides are congruent. ItsSchläfli symbolis {16} and can be constructed as atruncated octagon,t{8}, and a twice-truncatedsquarett{4}. A truncated hexadecagon, t{16}, is a triacontadigon, {32}.

Construction[edit]

As 16 = 2⁴(apower of two), a regular hexadecagon isconstructibleusingcompass and straightedge:this was already known to ancient Greek mathematicians.^[2]

Construction of a regular hexadecagon
at a given circumcircle

Construction of a regular hexadecagon
at a given side length, animation. (The construction is very similar to that ofoctagon at a given side length.)

Measurements[edit]

Each angle of a regular hexadecagon is 157.5degrees,and the total angle measure of any hexadecagon is 2520 degrees.

Theareaof a regular hexadecagon with edge lengthtis

{\begin{aligned}A=4t^{2}\cot {\frac {\pi }{16}}=&4t^{2}\left(1+{\sqrt {2}}+{\sqrt {4+2{\sqrt {2}}}}\right)\\=&4t^{2}({\sqrt {2}}+1)({\sqrt {4-2{\sqrt {2}}}}+1).\end{aligned}}

Because the hexadecagon has a number of sides that is apower of two,its area can be computed in terms of thecircumradiusRby truncatingViète's formula:

A=R^{2}\cdot {\frac {2}{1}}\cdot {\frac {2}{\sqrt {2}}}\cdot {\frac {2}{\sqrt {2+{\sqrt {2}}}}}=4R^{2}{\sqrt {2-{\sqrt {2}}}}.

Since the area of the circumcircle is $\pi R^{2},$ the regular hexadecagon fills approximately 97.45% of its circumcircle.

Symmetry[edit]

Symmetry
	The 14 symmetries of a regular hexadecagon. Lines of reflections are blue through vertices, purple through edges, and gyration orders are given in the center. Vertices are colored by their symmetry position.

Theregular hexadecagonhas Dih₁₆symmetry, order 32. There are 4 dihedral subgroups: Dih₈,Dih₄,Dih₂,and Dih₁,and 5cyclic subgroups:Z₁₆,Z₈,Z₄,Z₂,and Z₁,the last implying no symmetry.

On the regular hexadecagon, there are 14 distinct symmetries. John Conway labels full symmetry asr32and no symmetry is labeleda1.The dihedral symmetries are divided depending on whether they pass through vertices (dfor diagonal) or edges (pfor perpendiculars) Cyclic symmetries in the middle column are labeled asgfor their central gyration orders.^[3]

The most common high symmetry hexadecagons ared16,anisogonalhexadecagon constructed by eight mirrors can alternate long and short edges, andp16,anisotoxalhexadecagon constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms aredualsof each other and have half the symmetry order of the regular hexadecagon.

Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only theg16subgroup has no degrees of freedom but can be seen asdirected edges.

Dissection[edit]

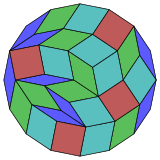
16-cubeprojection	112 rhomb dissection
	Regular	Isotoxal

Coxeterstates that everyzonogon(a 2m-gon whose opposite sides are parallel and of equal length) can be dissected intom(m-1)/2 parallelograms. ^[4] In particular this is true forregular polygonswith evenly many sides, in which case the parallelograms are all rhombi. For theregular hexadecagon,m=8, and it can be divided into 28: 4 squares and 3 sets of 8 rhombs. This decomposition is based on aPetrie polygonprojection of an8-cube,with 28 of 1792 faces. The listOEIS:A006245enumerates the number of solutions as 1232944, including up to 16-fold rotations and chiral forms in reflection.

Dissection into 28 rhombs
8-cube

Skew hexadecagon[edit]

3 regular skew zig-zag hexadecagon
{8}#{ }	{8⁄3}#{ }	{8⁄5}#{ }

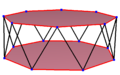
A regular skew hexadecagon is seen as zig-zagging edges of anoctagonal antiprism,anoctagrammic antiprism,and anoctagrammic crossed-antiprism.

Askew hexadecagonis askew polygonwith 24 vertices and edges but not existing on the same plane. The interior of such a hexadecagon is not generally defined. Askew zig-zag hexadecagonhas vertices alternating between two parallel planes.

Aregular skew hexadecagonisvertex-transitivewith equal edge lengths. In 3-dimensions it will be a zig-zag skew hexadecagon and can be seen in the vertices and side edges of anoctagonal antiprismwith the same D_8d,[2⁺,16] symmetry, order 32. Theoctagrammic antiprism,s{2,16/3} andoctagrammic crossed-antiprism,s{2,16/5} also have regular skew octagons.

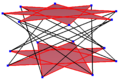
Petrie polygons[edit]

The regular hexadecagon is thePetrie polygonfor many higher-dimensional polytopes, shown in these skeworthogonal projections,including:

A₁₅	B₈		D₉		2B₂(4D)
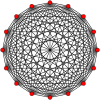15-simplex	8-orthoplex	8-cube	6₁₁	1₆₁	8-8 duopyramid	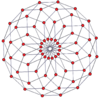8-8 duoprism

Related figures[edit]

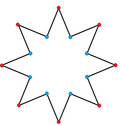
Ahexadecagramis a 16-sided star polygon, represented by symbol {16/n}. There are three regularstar polygons,{16/3}, {16/5}, {16/7}, using the same vertices, but connecting every third, fifth or seventh points. There are also three compounds: {16/2} is reduced to 2{8} as twooctagons,{16/4} is reduced to 4{4} as four squares and {16/6} reduces to 2{8/3} as twooctagrams,and finally {16/8} is reduced to 8{2} as eightdigons.

Compound and star hexadecagons
Form	Convex polygon	Compound	Star polygon	Compound
Image	{16/1} or {16}	{16/2} or 2{8}	{16/3}	{16/4} or 4{4}
Interior angle	157.5°	135°	112.5°	90°
Form	Star polygon	Compound	Star polygon	Compound
Image	{16/5}	{16/6} or 2{8/3}	{16/7}	{16/8} or 8{2}
Interior angle	67.5°	45°	22.5°	0°

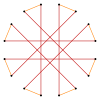
Deeper truncations of the regular octagon and octagram can produce isogonal (vertex-transitive) intermediate hexadecagram forms with equally spaced vertices and two edge lengths.^[5]

A truncated octagon is a hexadecagon, t{8}={16}. A quasitruncated octagon, inverted as {8/7}, is a hexadecagram: t{8/7}={16/7}. A truncated octagram {8/3} is a hexadecagram: t{8/3}={16/3} and a quasitruncated octagram, inverted as {8/5}, is a hexadecagram: t{8/5}={16/5}.

Isogonal truncations of octagon and octagram
Quasiregular	Isogonal	Quasiregular
t{8}={16}		t{8/7}={16/7}
t{8/3}={16/3}		t{8/5}={16/5}

In art[edit]

In the early 16th century,Raphaelwas the first to construct aperspectiveimage of a regular hexadecagon: the tower in his paintingThe Marriage of the Virginhas 16 sides, elaborating on an eight-sided tower in a previous painting byPietro Perugino.^[6]

A hexadecagrammic pattern from theAlhambra

Hexadecagrams (16-sidedstar polygons) are included in theGirihpatterns in theAlhambra.^[7]

Irregular hexadecagons[edit]

Anoctagonal starcan be seen as a concave hexadecagon:

The latter one is seen in many architectures from Christian to Islamic, and also in the logo ofIRIB TV4.

References[edit]

^Weisstein, Eric W. (2002).CRC Concise Encyclopedia of Mathematics, Second Edition.CRC Press. p. 1365.ISBN 9781420035223.
^Koshy, Thomas (2007),Elementary Number Theory with Applications(2nd ed.), Academic Press, p. 142,ISBN 9780080547091.
^John H. Conway, Heidi Burgiel,Chaim Goodman-Strauss,(2008) The Symmetries of Things,ISBN 978-1-56881-220-5(Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
^Coxeter,Mathematical recreations and Essays, Thirteenth edition, p.141
^The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994),Metamorphoses of polygons,Branko Grünbaum
^Speiser, David (2011), "Architecture, mathematics and theology in Raphael's paintings", inWilliams, Kim(ed.),Crossroads: History of Science, History of Art. Essays by David Speiser, vol. II,Springer, pp. 29–39,doi:10.1007/978-3-0348-0139-3_3.Originally published inNexus III: Architecture and Mathematics,Kim Williams,ed. (Ospedaletto, Pisa: Pacini Editore, 2000), pp. 147–156.
^Hankin, E. Hanbury (May 1925), "Examples of methods of drawing geometrical arabesque patterns",The Mathematical Gazette,12(176): 370–373,doi:10.2307/3604213.

External links[edit]

Weisstein, Eric W."Hexadecagon".MathWorld.

[Weisstein2002-1] Weisstein, Eric W. (2002).CRC Concise Encyclopedia of Mathematics, Second Edition.CRC Press. p. 1365.ISBN 9781420035223.

[2] Koshy, Thomas (2007),Elementary Number Theory with Applications(2nd ed.), Academic Press, p. 142,ISBN 9780080547091.

[3] John H. Conway, Heidi Burgiel,Chaim Goodman-Strauss,(2008) The Symmetries of Things,ISBN 978-1-56881-220-5(Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)

[4] Coxeter,Mathematical recreations and Essays, Thirteenth edition, p.141

[5] The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994),Metamorphoses of polygons,Branko Grünbaum

[6] Speiser, David (2011), "Architecture, mathematics and theology in Raphael's paintings", inWilliams, Kim(ed.),Crossroads: History of Science, History of Art. Essays by David Speiser, vol. II,Springer, pp. 29–39,doi:10.1007/978-3-0348-0139-3_3.Originally published inNexus III: Architecture and Mathematics,Kim Williams,ed. (Ospedaletto, Pisa: Pacini Editore, 2000), pp. 147–156.

[7] Hankin, E. Hanbury (May 1925), "Examples of methods of drawing geometrical arabesque patterns",The Mathematical Gazette,12(176): 370–373,doi:10.2307/3604213.

[1]

[2]

[3]

[4]

[5]

[6]

[7]