Hyperboloid

Hyperboloid of one sheet	conical surfacein between	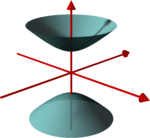Hyperboloid of two sheets

Ingeometry,ahyperboloid of revolution,sometimes called acircular hyperboloid,is thesurfacegenerated by rotating ahyperbolaaround one of itsprincipal axes.Ahyperboloidis the surface obtained from a hyperboloid of revolution by deforming it by means of directionalscalings,or more generally, of anaffine transformation.

A hyperboloid is aquadric surface,that is, asurfacedefined as thezero setof apolynomialof degree two in three variables. Among quadric surfaces, a hyperboloid is characterized by not being aconeor acylinder,having acenter of symmetry,and intersecting manyplanesinto hyperbolas. A hyperboloid has three pairwiseperpendicular axes of symmetry,and three pairwise perpendicularplanes of symmetry.

Given a hyperboloid, one can choose aCartesian coordinate systemsuch that the hyperboloid is defined by one of the following equations: ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1,$ or ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1.$ The coordinate axes are axes of symmetry of the hyperboloid and the origin is the center of symmetry of the hyperboloid. In any case, the hyperboloid isasymptoticto the cone of the equations: ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0.$

One has a hyperboloid of revolution if and only if $a^{2}=b^{2}.$ Otherwise, the axes are uniquely defined (up tothe exchange of thex-axis and they-axis).

There are two kinds of hyperboloids. In the first case ( $+1$ in the right-hand side of the equation): aone-sheet hyperboloid,also called ahyperbolic hyperboloid.It is aconnected surface,which has a negativeGaussian curvatureat every point. This implies near every point the intersection of the hyperboloid and itstangent planeat the point consists of two branches of curve that have distinct tangents at the point. In the case of the one-sheet hyperboloid, these branches of curves arelinesand thus the one-sheet hyperboloid is adoubly ruledsurface.

In the second case ( $-1$ in the right-hand side of the equation): atwo-sheet hyperboloid,also called anelliptic hyperboloid.The surface has twoconnected componentsand a positive Gaussian curvature at every point. The surface isconvexin the sense that the tangent plane at every point intersects the surface only in this point.

Parametric representations

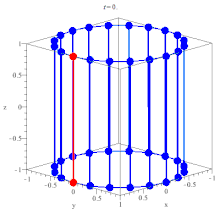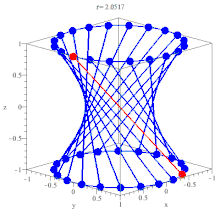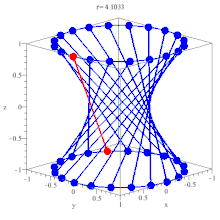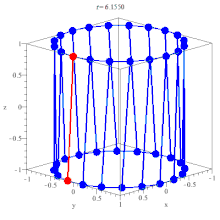
Cartesian coordinates for the hyperboloids can be defined, similar tospherical coordinates,keeping theazimuthangle $θ \in [0, 2 π)$ ,but changing inclination $v$ intohyperbolic trigonometric functions:

One-surface hyperboloid: $v \in (-\infty, \infty)$ ${\begin{aligned}x&=a\cosh v\cos \theta \\y&=b\cosh v\sin \theta \\z&=c\sinh v\end{aligned}}$

Two-surface hyperboloid: $v \in [0, \infty)$ ${\begin{aligned}x&=a\sinh v\cos \theta \\y&=b\sinh v\sin \theta \\z&=\pm c\cosh v\end{aligned}}$

hyperboloid of one sheet: generation by a rotating hyperbola (top) and line (bottom: red or blue)

hyperboloid of one sheet: plane sections

The following parametric representation includes hyperboloids of one sheet, two sheets, and their common boundary cone, each with the $z$ -axis as the axis of symmetry: $\mathbf {x} (s,t)=\left({\begin{array}{lll}a{\sqrt {s^{2}+d}}\cos t\\b{\sqrt {s^{2}+d}}\sin t\\cs\end{array}}\right)$

For $d>0$ one obtains a hyperboloid of one sheet,
For $d<0$ a hyperboloid of two sheets, and
For $d=0$ a double cone.

One can obtain a parametric representation of a hyperboloid with a different coordinate axis as the axis of symmetry by shuffling the position of the $cs$ term to the appropriate component in the equation above.

Generalised equations

More generally, an arbitrarily oriented hyperboloid, centered at $v$ ,is defined by the equation $(\mathbf {x} -\mathbf {v} )^{\mathrm {T} }A(\mathbf {x} -\mathbf {v} )=1,$ where $A$ is amatrixand $x$ , $v$ arevectors.

Theeigenvectorsof $A$ define the principal directions of the hyperboloid and theeigenvaluesof A are thereciprocalsof the squares of the semi-axes: ${1/a^{2}}$ , ${1/b^{2}}$ and ${1/c^{2}}$ .The one-sheet hyperboloid has two positive eigenvalues and one negative eigenvalue. The two-sheet hyperboloid has one positive eigenvalue and two negative eigenvalues.

Properties

Hyperboloid of one sheet

Lines on the surface

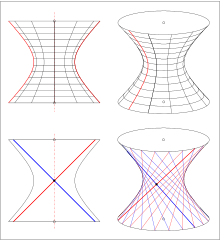
A hyperboloid of one sheet contains two pencils of lines. It is adoubly ruled surface.

If the hyperboloid has the equation ${x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1$ then the lines

$g_{\alpha }^{\pm }:\mathbf {x} (t)={\begin{pmatrix}a\cos \alpha \\b\sin \alpha \\0\end{pmatrix}}+t\cdot {\begin{pmatrix}-a\sin \alpha \\b\cos \alpha \\\pm c\end{pmatrix}}\,\quad t\in \mathbb {R},\ 0\leq \alpha \leq 2\pi \$ are contained in the surface.

In case $a=b$ the hyperboloid is a surface of revolution and can be generated by rotating one of the two lines $g_{0}^{+}$ or $g_{0}^{-}$ ,which are skew to the rotation axis (see picture). This property is calledWren's theorem.^[1]The more common generation of a one-sheet hyperboloid of revolution is rotating ahyperbolaaround itssemi-minor axis(see picture; rotating the hyperbola around its other axis gives a two-sheet hyperbola of revolution).

A hyperboloid of one sheet isprojectivelyequivalent to ahyperbolic paraboloid.

Plane sections

For simplicity the plane sections of theunit hyperboloidwith equation $\ H_{1}:x^{2}+y^{2}-z^{2}=1$ are considered. Because a hyperboloid in general position is an affine image of the unit hyperboloid, the result applies to the general case, too.

A plane with a slope less than 1 (1 is the slope of the lines on the hyperboloid) intersects $H_{1}$ in anellipse,
A plane with a slope equal to 1 containing the origin intersects $H_{1}$ in apair of parallel lines,
A plane with a slope equal 1 not containing the origin intersects $H_{1}$ in aparabola,
A tangential plane intersects $H_{1}$ in apair of intersecting lines,
A non-tangential plane with a slope greater than 1 intersects $H_{1}$ in ahyperbola.^[2]

Obviously, any one-sheet hyperboloid of revolution contains circles. This is also true, but less obvious, in the general case (seecircular section).

Hyperboloid of two sheets

The hyperboloid of two sheets doesnotcontain lines. The discussion of plane sections can be performed for theunit hyperboloid of two sheetswith equation $H_{2}:\ x^{2}+y^{2}-z^{2}=-1.$ which can be generated by a rotatinghyperbolaaround one of its axes (the one that cuts the hyperbola)

A plane with slope less than 1 (1 is the slope of the asymptotes of the generating hyperbola) intersects $H_{2}$ either in anellipseor in apointor not at all,
A plane with slope equal to 1 containing the origin (midpoint of the hyperboloid) doesnot intersect $H_{2}$ ,
A plane with slope equal to 1 not containing the origin intersects $H_{2}$ in aparabola,
A plane with slope greater than 1 intersects $H_{2}$ in ahyperbola.^[3]

Obviously, any two-sheet hyperboloid of revolution contains circles. This is also true, but less obvious, in the general case (seecircular section).

Remark:A hyperboloid of two sheets isprojectivelyequivalent to a sphere.

Other properties

Symmetries

The hyperboloids with equations ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1,\quad {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=-1$ are

pointsymmetricto the origin,
symmetric to the coordinate planesand
rotational symmetricto the z-axis and symmetric to any plane containing the z-axis, in case of $a=b$ (hyperboloid of revolution).

Curvature

Whereas theGaussian curvatureof a hyperboloid of one sheet is negative, that of a two-sheet hyperboloid is positive. In spite of its positive curvature, the hyperboloid of two sheets with another suitably chosen metric can also be used as amodelfor hyperbolic geometry.

In more than three dimensions

Imaginary hyperboloids are frequently found in mathematics of higher dimensions. For example, in apseudo-Euclidean spaceone has the use of aquadratic form: $q(x)=\left(x_{1}^{2}+\cdots +x_{k}^{2}\right)-\left(x_{k+1}^{2}+\cdots +x_{n}^{2}\right),\quad k<n.$ When $c$ is anyconstant,then the part of the space given by $\lbrace x\:\ q(x)=c\rbrace$ is called ahyperboloid.The degenerate case corresponds to $c = 0$ .

As an example, consider the following passage:^[4]

... the velocity vectors always lie on a surface which Minkowski calls a four-dimensional hyperboloid since, expressed in terms of purely real coordinates $(y 1,..., y 4)$ ,its equation is $y 21 + y 22 + y 23 - y 24 = -1$ ,analogous to the hyperboloid $y 21 + y 22 - y 23 = -1$ of three-dimensional space.^[6]

However, the termquasi-sphereis also used in this context since the sphere and hyperboloid have some commonality (See§ Relation to the spherebelow).

Hyperboloid structures

One-sheeted hyperboloids are used in construction, with the structures calledhyperboloid structures.A hyperboloid is adoubly ruled surface;thus, it can be built with straight steel beams, producing a strong structure at a lower cost than other methods. Examples includecooling towers,especially ofpower stations,andmany other structures.

Gallery of one sheet hyperboloid structures
TheAdziogol Lighthouse,Ukraine,1911.
The first 1916 patentedVan Iterson cooling towerofDSM EmmainHeerlen,The Netherlands,1918
Kobe Port Tower,Japan,1963.
Saint Louis Science Center's James S.McDonnell Planetarium,St. Louis,Missouri,1963.
Newcastle International Airportcontrol tower,Newcastle upon Tyne,England,1967.
Ještěd Transmission Tower,Czech Republic,1968.
Cathedral of Brasília,Brazil,1970.
Hyperboloid water towerwithtoroidaltank,Ciechanów,Poland,1972.
Roy Thomson Hall,Toronto,Canada,1982.
TheTHTR-300 cooling towerfor the now decommissionedthorium nuclear reactorinHamm-Uentrop,Germany,1983.
TheCorporation Street Bridge,Manchester,England,1999.
TheKillesbergobservation tower,Stuttgart,Germany,2001.
BMW Welt,(BMW World), museum and event venue,Munich,Germany,2007.
TheCanton Tower,China,2010.
TheEssarts-le-Roiwater tower,France.

Relation to the sphere

In 1853William Rowan Hamiltonpublished hisLectures on Quaternionswhich included presentation ofbiquaternions.The following passage from page 673 shows how Hamilton uses biquaternion algebra and vectors fromquaternionsto produce hyperboloids from the equation of asphere:

... theequation of the unit sphere $ρ 2 + 1 = 0$ ,and change the vector $ρ$ to abivector form,such as $σ + τ \sqrt -1$ .The equation of the sphere then breaks up into the system of the two following,
$σ 2 - τ 2 + 1 = 0$ , $S . στ = 0$ ;

and suggests our considering $σ$ and $τ$ as two real and rectangular vectors, such that

$T τ = (T σ 2 - 1 ) 1/2$ .
Hence it is easy to infer that if we assume $σ || λ$ ,where $λ$ is a vector in a given position, thenew real vector $σ + τ$ will terminate on the surface of adouble-sheeted and equilateral hyperboloid;and that if, on the other hand, we assume $τ || λ$ ,then the locus of the extremity of the real vector $σ + τ$ will be anequilateral but single-sheeted hyperboloid.The study of these two hyperboloids is, therefore, in this way connected very simply, through biquaternions, with the study of the sphere;...

In this passage $S$ is the operator giving the scalar part of a quaternion, and $T$ is the "tensor", now callednorm,of a quaternion.

A modern view of the unification of the sphere and hyperboloid uses the idea of aconic sectionas aslice of a quadratic form.Instead of aconical surface,one requires conicalhypersurfacesinfour-dimensional spacewith points $p = (w, x, y, z) \in R 4$ determined byquadratic forms.First consider the conical hypersurface

$P=\left\{p\;:\;w^{2}=x^{2}+y^{2}+z^{2}\right\}$ and
$H_{r}=\lbrace p\:\ w=r\rbrace,$ which is ahyperplane.

Then $P\cap H_{r}$ is the sphere with radius $r$ .On the other hand, the conical hypersurface

Q=\lbrace p\:\ w^{2}+z^{2}=x^{2}+y^{2}\rbrace

provides that

Q\cap H_{r}

is a hyperboloid.

In the theory ofquadratic forms,aunitquasi-sphereis the subset of a quadratic space $X$ consisting of the $x \in X$ such that the quadratic norm of $x$ is one.^[7]

References

^K. Strubecker:Vorlesungen der Darstellenden Geometrie.Vandenhoeck & Ruprecht, Göttingen 1967, p. 218
^CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie (TU Darmstadt)(PDF; 3,4 MB), S. 116
^CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie (TU Darmstadt)(PDF; 3,4 MB), S. 122
^Thomas Hawkins (2000)Emergence of the Theory of Lie Groups: an essay in the history of mathematics, 1869—1926,§9.3 "The Mathematization of Physics at Göttingen", see page 340, SpringerISBN 0-387-98963-3
^Walter, Scott A. (1999),"The non-Euclidean style of Minkowskian relativity",in J. Gray (ed.),The Symbolic Universe: Geometry and Physics 1890-1930,Oxford University Press, pp. 91–127
^Minkowski used the term "four-dimensional hyperboloid" only once, in a posthumously-published typescript and this was non-standard usage, as Minkowski's hyperboloid is a three-dimensional submanifold of a four-dimensional Minkowski space $M^{4}.$ ^[5]
^Ian R. Porteous(1995)Clifford Algebras and the Classical Groups,pages 22, 24 & 106,Cambridge University PressISBN 0-521-55177-3

Wilhelm Blaschke(1948)Analytische Geometrie,Kapital V: "Quadriken", Wolfenbutteler Verlagsanstalt.
David A. Brannan, M. F. Esplen, & Jeremy J Gray (1999)Geometry,pp. 39–41Cambridge University Press.
H. S. M. Coxeter(1961)Introduction to Geometry,p. 130,John Wiley & Sons.

External links

Weisstein, Eric W."Hyperboloid".MathWorld.

[1] K. Strubecker:Vorlesungen der Darstellenden Geometrie.Vandenhoeck & Ruprecht, Göttingen 1967, p. 218

[2] CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie (TU Darmstadt)(PDF; 3,4 MB), S. 116

[3] CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie (TU Darmstadt)(PDF; 3,4 MB), S. 122

[4] Thomas Hawkins (2000)Emergence of the Theory of Lie Groups: an essay in the history of mathematics, 1869—1926,§9.3 "The Mathematization of Physics at Göttingen", see page 340, SpringerISBN 0-387-98963-3

[5] Walter, Scott A. (1999),"The non-Euclidean style of Minkowskian relativity",in J. Gray (ed.),The Symbolic Universe: Geometry and Physics 1890-1930,Oxford University Press, pp. 91–127

[6] Minkowski used the term "four-dimensional hyperboloid" only once, in a posthumously-published typescript and this was non-standard usage, as Minkowski's hyperboloid is a three-dimensional submanifold of a four-dimensional Minkowski space $M^{4}.$ ^[5]

[7] Ian R. Porteous(1995)Clifford Algebras and the Classical Groups,pages 22, 24 & 106,Cambridge University PressISBN 0-521-55177-3

[1]

[2]

[3]

[4]

[6]

[7]

[5]