AM–GM inequality
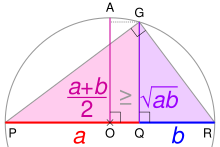
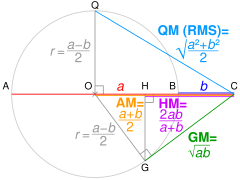
PR is the diameter of a circle centered on O; its radius AO is thearithmetic meanofaandb.Using thegeometric mean theorem,triangle PGR'saltitudeGQ is thegeometric mean.For any ratioa:b,AO ≥ GQ.
Inmathematics,theinequality of arithmetic and geometric means,or more briefly theAM–GM inequality,states that thearithmetic meanof a list of non-negativereal numbersis greater than or equal to thegeometric meanof the same list; and further, that the two means are equalif and only ifevery number in the list is the same (in which case they are both that number).
The simplest non-trivial case – i.e., with more than one variable – for two non-negative numbersxandy,is the statement that
with equality if and only ifx=y. This case can be seen from the fact that the square of a real number is always non-negative (greater than or equal to zero) and from the elementary case(a±b)2=a2± 2ab+b2of thebinomial formula:
Hence(x+y)2≥ 4xy,with equality precisely when(x−y)2= 0,i.e.x=y.The AM–GM inequality then follows from taking the positive square root of both sides and then dividing both sides by2.
For a geometrical interpretation, consider arectanglewith sides of lengthxandy,hence it hasperimeter2x+ 2yandareaxy.Similarly, asquarewith all sides of length√xyhas the perimeter4√xyand the same area as the rectangle. The simplest non-trivial case of the AM–GM inequality implies for the perimeters that2x+ 2y≥ 4√xyand that only the square has the smallest perimeter amongst all rectangles of equal area.
The simplest case is implicit inEuclid's Elements,Book 5, Proposition 25.[2]
Extensions of the AM–GM inequality are available to includeweightsorgeneralized means.
Background[edit]
Thearithmetic mean,or less precisely theaverage,of a list ofnnumbersx1,x2,...,xnis the sum of the numbers divided byn:
Thegeometric meanis similar, except that it is only defined for a list ofnonnegativereal numbers, and uses multiplication and arootin place of addition and division:
Ifx1,x2,...,xn> 0,this is equal to theexponentialof the arithmetic mean of thenatural logarithmsof the numbers:
Note: This does not apply exclusively to the exp() function and natural logarithms. The base b of the exponentiation could be any positive real number if the logarithm is of base b.
The inequality[edit]
Restating the inequality using mathematical notation, we have that for any list ofnnonnegative real numbersx1,x2,...,xn,
and that equality holds if and only ifx1=x2= · · · =xn.
Geometric interpretation[edit]
In two dimensions,2x1+ 2x2is theperimeterof a rectangle with sides of lengthx1andx2.Similarly,4√x1x2is the perimeter of a square with the samearea,x1x2,as that rectangle. Thus forn= 2the AM–GM inequality states that a rectangle of a given area has the smallest perimeter if that rectangle is also a square.
The full inequality is an extension of this idea tondimensions. Consider ann-dimensional box with edge lengthsx1,x2,...,xn. Every vertex of the box is connected tonedges of different directions, so the average length of edges incident to the vertex is(x1+x2+ · · · +xn)/n. On the other hand,is the edge length of ann-dimensional cube of equal volume, which therefore is also the average length of edges incident to a vertex of the cube.
Thus the AM–GM inequality states that only then-cubehas the smallest average length of edges connected to each vertex amongst alln-dimensional boxes with the same volume.[3]
Examples[edit]
Example 1[edit]
If,then the A.M.-G.M. tells us that
Example 2[edit]
A simple upper bound forcan be found. AM-GM tells us
and so
with equality at.
Equivalently,
Example 3[edit]
Consider the function
for all positive real numbersx,yandz.Suppose we wish to find the minimal value of this function. It can be rewritten as:
with
Applying the AM–GM inequality forn= 6,we get
Further, we know that the two sides are equal exactly when all the terms of the mean are equal:
All the points(x,y,z)satisfying these conditions lie on a half-line starting at the origin and are given by
Applications[edit]
An important practical application infinancial mathematicsis to computing therate of return:theannualized return,computed via the geometric mean, is less than the average annual return, computed by the arithmetic mean (or equal if all returns are equal). This is important in analyzinginvestments,as the average return overstates the cumulative effect. It can also be used to prove theCauchy–Schwarz inequality.
Proofs of the AM–GM inequality[edit]
The AM–GM inequality is also known for the variety of methods that can be used to prove it.
Proof using Jensen's inequality[edit]
Jensen's inequalitystates that the value of aconcave functionof an arithmetic mean is greater than or equal to the arithmetic mean of the function's values. Since thelogarithmfunction is concave, we have
Takingantilogsof the far left and far right sides, we have the AM–GM inequality.
Proof by successive replacement of elements[edit]
We have to show that
with equality only when all numbers are equal.
If not all numbers are equal, then there existsuch that.Replacingxibyandxjbywill leave the arithmetic mean of the numbers unchanged, but will increase the geometric mean because
If the numbers are still not equal, we continue replacing numbers as above. After at mostsuch replacement steps all the numbers will have been replaced withwhile the geometric mean strictly increases at each step. After the last step, the geometric mean will be,proving the inequality.
It may be noted that the replacement strategy works just as well from the right hand side. If any of the numbers is 0 then so will the geometric mean thus proving the inequality trivially. Therefore we may suppose that all the numbers are positive. If they are not all equal, then there existsuch that.Replacingbyandbyleaves the geometric mean unchanged but strictly decreases the arithmetic mean since
- .The proof then follows along similar lines as in the earlier replacement.
Induction proofs[edit]
Proof by induction #1[edit]
Of the non-negative real numbersx1,...,xn,the AM–GM statement is equivalent to
with equality if and only ifα=xifor alli∈ {1,...,n}.
For the following proof we applymathematical inductionand only well-known rules of arithmetic.
Induction basis:Forn= 1the statement is true with equality.
Induction hypothesis:Suppose that the AM–GM statement holds for all choices ofnnon-negative real numbers.
Induction step:Considern+ 1non-negative real numbersx1,...,xn+1,.Their arithmetic meanαsatisfies
If all thexiare equal toα,then we have equality in the AM–GM statement and we are done. In the case where some are not equal toα,there must exist one number that is greater than the arithmetic meanα,and one that is smaller thanα.Without loss of generality, we can reorder ourxiin order to place these two particular elements at the end:xn>αandxn+1<α.Then
Now defineywith
and consider thennumbersx1,...,xn–1,ywhich are all non-negative. Since
Thus,αis also the arithmetic mean ofnnumbersx1,...,xn–1,yand the induction hypothesis implies
Due to (*) we know that
hence
in particularα> 0.Therefore, if at least one of the numbersx1,...,xn–1is zero, then we already have strict inequality in (**). Otherwise the right-hand side of (**) is positive and strict inequality is obtained by using the estimate (***) to get a lower bound of the right-hand side of (**). Thus, in both cases we can substitute (***) into (**) to get
which completes the proof.
Proof by induction #2[edit]
First of all we shall prove that for real numbersx1< 1andx2> 1there follows
Indeed, multiplying both sides of the inequalityx2> 1by1 –x1,gives
whence the required inequality is obtained immediately.
Now, we are going to prove that for positive real numbersx1,...,xnsatisfying x1...xn= 1,there holds
The equality holds only ifx1=... =xn= 1.
Induction basis:Forn= 2the statement is true because of the above property.
Induction hypothesis:Suppose that the statement is true for all natural numbers up ton– 1.
Induction step:Consider natural numbern,i.e. for positive real numbersx1,...,xn,there holdsx1...xn= 1.There exists at least onexk< 1,so there must be at least onexj> 1.Without loss of generality, we letk=n– 1andj=n.
Further, the equalityx1...xn= 1we shall write in the form of(x1...xn–2) (xn–1xn) = 1.Then, the induction hypothesis implies
However, taking into account the induction basis, we have
which completes the proof.
For positive real numbersa1,...,an,let's denote
The numbersx1,...,xnsatisfy the conditionx1...xn= 1.So we have
whence we obtain
with the equality holding only fora1=... =an.
Proof by Cauchy using forward–backward induction[edit]
The following proof by cases relies directly on well-known rules of arithmetic but employs the rarely used technique of forward-backward-induction. It is essentially fromAugustin Louis Cauchyand can be found in hisCours d'analyse.[4]
The case where all the terms are equal[edit]
If all the terms are equal:
then their sum isnx1,so their arithmetic mean isx1;and their product isx1n,so their geometric mean isx1;therefore, the arithmetic mean and geometric mean are equal, as desired.
The case where not all the terms are equal[edit]
It remains to show that ifnotall the terms are equal, then the arithmetic mean is greater than the geometric mean. Clearly, this is only possible whenn> 1.
This case is significantly more complex, and we divide it into subcases.
The subcase wheren= 2[edit]
Ifn= 2,then we have two terms,x1andx2,and since (by our assumption) not all terms are equal, we have:
hence
as desired.
The subcase wheren= 2k[edit]
Consider the case wheren= 2k,wherekis a positive integer. We proceed by mathematical induction.
In the base case,k= 1,son= 2.We have already shown that the inequality holds whenn= 2,so we are done.
Now, suppose that for a givenk> 1,we have already shown that the inequality holds forn= 2k−1,and we wish to show that it holds forn= 2k.To do so, we apply the inequality twice for2k-1numbers and once for2numbers to obtain:
where in the first inequality, the two sides are equal only if
and
(in which case the first arithmetic mean and first geometric mean are both equal tox1,and similarly with the second arithmetic mean and second geometric mean); and in the second inequality, the two sides are only equal if the two geometric means are equal. Since not all2knumbers are equal, it is not possible for both inequalities to be equalities, so we know that:
as desired.
The subcase wheren< 2k[edit]
Ifnis not a natural power of2,then it is certainlylessthan some natural power of 2, since the sequence2, 4, 8,..., 2k,...is unbounded above. Therefore, without loss of generality, letmbe some natural power of2that is greater thann.
So, if we haventerms, then let us denote their arithmetic mean byα,and expand our list of terms thus:
We then have:
so
and
as desired.
Proof by induction using basic calculus[edit]
The following proof uses mathematical induction and some basicdifferential calculus.
Induction basis:Forn= 1the statement is true with equality.
Induction hypothesis:Suppose that the AM–GM statement holds for all choices ofnnon-negative real numbers.
Induction step:In order to prove the statement forn+ 1non-negative real numbersx1,...,xn,xn+1,we need to prove that
with equality only if all then+ 1numbers are equal.
If all numbers are zero, the inequality holds with equality. If some but not all numbers are zero, we have strict inequality. Therefore, we may assume in the following, that alln+ 1numbers are positive.
We consider the last numberxn+1as a variable and define the function
Proving the induction step is equivalent to showing thatf(t) ≥ 0for allt> 0,withf(t) = 0only ifx1,...,xnandtare all equal. This can be done by analyzing thecritical pointsoffusing some basic calculus.
The firstderivativeoffis given by
A critical pointt0has to satisfyf′(t0) = 0,which means
After a small rearrangement we get
and finally
which is the geometric mean ofx1,...,xn.This is the only critical point off.Sincef′′(t) > 0for allt> 0,the functionfisstrictly convexand has a strictglobal minimumatt0.Next we compute the value of the function at this global minimum:
where the final inequality holds due to the induction hypothesis. The hypothesis also says that we can have equality only whenx1,...,xnare all equal. In this case, their geometric meant0has the same value, Hence, unlessx1,...,xn,xn+1are all equal, we havef(xn+1) > 0.This completes the proof.
This technique can be used in the same manner to prove the generalized AM–GM inequality andCauchy–Schwarz inequalityin Euclidean spaceRn.
Proof by Pólya using the exponential function[edit]
George Pólyaprovided a proof similar to what follows. Letf(x) = ex–1–xfor all realx,with firstderivativef′(x) = ex–1– 1and second derivativef′′(x) = ex–1.Observe thatf(1) = 0,f′(1) = 0andf′′(x) > 0for all realx,hencefis strictly convex with the absolute minimum atx= 1.Hencex≤ ex–1for all realxwith equality only forx= 1.
Consider a list of non-negative real numbersx1,x2,...,xn.If they are all zero, then the AM–GM inequality holds with equality. Hence we may assume in the following for their arithmetic meanα> 0.Byn-fold application of the above inequality, we obtain that
with equality if and only ifxi=αfor everyi∈ {1,...,n}.The argument of the exponential function can be simplified:
Returning to(*),
which producesx1x2· · ·xn≤αn,hence the result[5]
Proof by Lagrangian multipliers[edit]
If any of theare,then there is nothing to prove. So we may assume all theare strictly positive.
Because the arithmetic and geometric means are homogeneous of degree 1, without loss of generality assume that.Set,and.The inequality will be proved (together with the equality case) if we can show that the minimum ofsubject to the constraintis equal to,and the minimum is only achieved when.Let us first show that the constrained minimization problem has a global minimum.
Set.Since the intersectionis compact, theextreme value theoremguarantees that the minimum ofsubject to the constraintsandis attained at some point inside.On the other hand, observe that if any of the,then,while,and.This means that the minimum insideis in fact a global minimum, since the value ofat any point insideis certainly no smaller than the minimum, and the value ofat any pointnot insideis strictly bigger than the value at,which is no smaller than the minimum.
The method ofLagrange multiplierssays that the global minimum is attained at a pointwhere the gradient ofistimes the gradient of,for some.We will show that the only point at which this happens is whenand
Compute and
along the constraint. Setting the gradients proportional to one another therefore gives for eachthatand soSince the left-hand side does not depend on,it follows that,and since,it follows thatand,as desired.
Generalizations[edit]
Weighted AM–GM inequality[edit]
There is a similar inequality for theweighted arithmetic meanandweighted geometric mean.Specifically, let the nonnegative numbersx1,x2,...,xnand the nonnegative weightsw1,w2,...,wnbe given. Setw=w1+w2+ · · · +wn.Ifw> 0,then the inequality
holds with equality if and only if all thexkwithwk> 0are equal. Here the convention00= 1is used.
If allwk= 1,this reduces to the above inequality of arithmetic and geometric means.
One stronger version of this, which also gives strengthened version of the unweighted version, is due to Aldaz. In particular, There is a similar inequality for theweighted arithmetic meanandweighted geometric mean.Specifically, let the nonnegative numbersx1,x2,...,xnand the nonnegative weightsw1,w2,...,wnbe given. Assume further that the sum of the weights is 1. Then
- .[6]
Proof using Jensen's inequality[edit]
Using the finite form ofJensen's inequalityfor thenatural logarithm,we can prove the inequality between the weighted arithmetic mean and the weighted geometric mean stated above.
Since anxkwith weightwk= 0has no influence on the inequality, we may assume in the following that all weights are positive. If allxkare equal, then equality holds. Therefore, it remains to prove strict inequality if they are not all equal, which we will assume in the following, too. If at least onexkis zero (but not all), then the weighted geometric mean is zero, while the weighted arithmetic mean is positive, hence strict inequality holds. Therefore, we may assume also that allxkare positive.
Since the natural logarithm isstrictly concave,the finite form of Jensen's inequality and thefunctional equationsof the natural logarithm imply
Since the natural logarithm isstrictly increasing,
Matrix arithmetic–geometric mean inequality[edit]
Most matrix generalizations of the arithmetic geometric mean inequality apply on the level of unitarily invariant norms, owing to the fact that even if the matricesandare positive semi-definite the matrixmay not be positive semi-definite and hence may not have a canonical square root. In[7]Bhatia and Kittaneh proved that for any unitarily invariant normand positive semi-definite matricesandit is the case that
Later, in[8]the same authors proved the stronger inequality that
Finally, it is known for dimensionthat the following strongest possible matrix generalization of the arithmetic-geometric mean inequality holds, and it is conjectured to hold for all
This conjectured inequality was shown by Stephen Drury in 2012. Indeed, he proved[9]
Finance: Link to geometric asset returns[edit]
In finance much research is concerned with accurately estimating therate of returnof an asset over multiple periods in the future. In the case of lognormal asset returns, there is an exact formula to compute the arithmetic asset return from the geometric asset return.
For simplicity, assume we are looking at yearly geometric returnsr1,r2,..., rNover a time horizon ofNyears, i.e.
where:
- = value of the asset at time,
- = value of the asset at time.
The geometric and arithmetic returns are respectively defined as
When the yearly geometric asset returns are lognormally distributed, then the following formula can be used to convert the geometric average return to the arithemtic average return:[10]
whereis thevarianceof the observed asset returns This implicit equation foraNcan be solved exactly as follows. First, notice that by setting
we obtain a polynomial equation of degree 2:
Solving this equation forzand using the definition ofz,we obtain 4 possible solutions foraN:
However, notice that
This implies that the only 2 possible solutions are (as asset returns are real numbers):
Finally, we expect the derivative ofaNwith respect togNto be non-negative as an increase in the geometric return should never cause a decrease in the arithmetic return. Indeed, both measure the average growth of an asset's value and therefore should move in similar directions. This leaves us with one solution to the implicit equation foraN,namely
Therefore, under the assumption of lognormally distributed asset returns, the arithmetic asset return is fully determined by the geometric asset return.
Other generalizations[edit]
Other generalizations of the inequality of arithmetic and geometric means include:
- Muirhead's inequality,
- Maclaurin's inequality,
- Generalized mean inequality,
- Means of complex numbers.[11]
See also[edit]
Notes[edit]
- ^If AC =aand BC =b.OC =AMofaandb,and radiusr= QO = OG.
UsingPythagoras' theorem,QC² = QO² + OC² ∴ QC = √QO² + OC²=QM.
Using Pythagoras' theorem, OC² = OG² + GC² ∴ GC = √OC² − OG²=GM.
Usingsimilar triangles,HC/GC=GC/OC∴ HC =GC²/OC=HM.
References[edit]
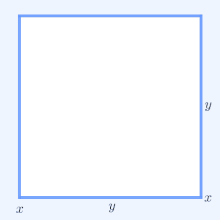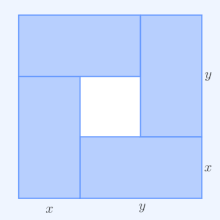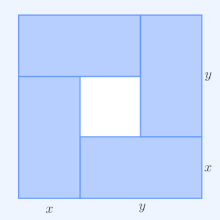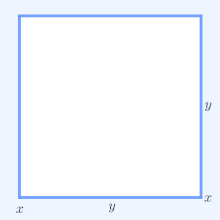
- ^Hoffman, D. G. (1981), "Packing problems and inequalities", inKlarner, David A.(ed.),The Mathematical Gardner,Springer, pp. 212–225,doi:10.1007/978-1-4684-6686-7_19,ISBN978-1-4684-6688-1
- ^"Euclid's Elements, Book V, Proposition 25".
- ^Steele, J. Michael (2004).The Cauchy-Schwarz Master Class: An Introduction to the Art of Mathematical Inequalities.MAA Problem Books Series. Cambridge University Press.ISBN978-0-521-54677-5.OCLC54079548.
- ^Cauchy, Augustin-Louis (1821).Cours d'analyse de l'École Royale Polytechnique, première partie, Analyse algébrique,Paris. The proof of the inequality of arithmetic and geometric means can be found on pages 457ff.
- ^Arnold, Denise; Arnold, Graham (1993).Four unit mathematics.Hodder Arnold H&S. p. 242.ISBN978-0-340-54335-1.OCLC38328013.
- ^Aldaz, J.M. (2009)."Self-Improvement of the Inequality Between Arithmetic and Geometric Means".Journal of Mathematical Inequalities.3(2): 213–216.doi:10.7153/jmi-03-21.Retrieved11 January2023.
- ^Bhatia, Rajendra; Kittaneh, Fuad (1990). "On the singular values of a product of operators".SIAM Journal on Matrix Analysis and Applications.11(2): 272–277.doi:10.1137/0611018.
- ^Bhatia, Rajendra; Kittaneh, Fuad (2000)."Notes on matrix arithmetic-geometric mean inequalities".Linear Algebra and Its Applications.308(1–3): 203–211.doi:10.1016/S0024-3795(00)00048-3.
- ^S.W. Drury, On a question of Bhatia and Kittaneh, Linear Algebra Appl. 437 (2012) 1955–1960.
- ^cf. Mindlin, Dimitry, On the Relationship between Arithmetic and Geometric Returns (August 14, 2011). Available at SSRN:https://ssrn.com/abstract=2083915orhttp://dx.doi.org/10.2139/ssrn.2083915
- ^cf. Iordanescu, R.; Nichita, F.F.; Pasarescu, O. Unification Theories: Means and Generalized Euler Formulas. Axioms 2020, 9, 144.
External links[edit]
- Arthur Lohwater (1982)."Introduction to Inequalities".Online e-book in PDF format.




![{\displaystyle {\sqrt[{n}]{x_{1}\cdot x_{2}\cdots x_{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b69ade737202da401cfb8245a9c21761def73427)

![{\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\geq {\sqrt[{n}]{x_{1}\cdot x_{2}\cdots x_{n}}}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b8fe0d05d569fcc62a418e9dcb8d7af19012387)
![{\displaystyle {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c293138a5d3ff3a9585ca9014322ec900db1e002)



![{\displaystyle 1+2+\dots +n\geq n{\sqrt[{n}]{n!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a07a96fe2d6cbdc2a0aed8247b5bfe22a6e3756)
![{\displaystyle {\frac {n(n+1)}{2}}\geq n{\sqrt[{n}]{n!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e56b5e562f06461bccfe684742e0e7f79f09704a)



![{\displaystyle f(x,y,z)={\frac {x}{y}}+{\sqrt {\frac {y}{z}}}+{\sqrt[{3}]{\frac {z}{x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63f82a8b0a26a3c022023901ce2c13231b8a9a7e)
![{\displaystyle {\begin{aligned}f(x,y,z)&=6\cdot {\frac {{\frac {x}{y}}+{\frac {1}{2}}{\sqrt {\frac {y}{z}}}+{\frac {1}{2}}{\sqrt {\frac {y}{z}}}+{\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}+{\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}+{\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}}{6}}\\&=6\cdot {\frac {x_{1}+x_{2}+x_{3}+x_{4}+x_{5}+x_{6}}{6}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53a43768e750d8a5fa46177fd450e7bfe197350c)
![{\displaystyle x_{1}={\frac {x}{y}},\qquad x_{2}=x_{3}={\frac {1}{2}}{\sqrt {\frac {y}{z}}},\qquad x_{4}=x_{5}=x_{6}={\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/286767799e6ff881d406a6a35694a5227f77de95)
![{\displaystyle {\begin{aligned}f(x,y,z)&\geq 6\cdot {\sqrt[{6}]{{\frac {x}{y}}\cdot {\frac {1}{2}}{\sqrt {\frac {y}{z}}}\cdot {\frac {1}{2}}{\sqrt {\frac {y}{z}}}\cdot {\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}\cdot {\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}\cdot {\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}}}\\&=6\cdot {\sqrt[{6}]{{\frac {1}{2\cdot 2\cdot 3\cdot 3\cdot 3}}{\frac {x}{y}}{\frac {y}{z}}{\frac {z}{x}}}}\\&=2^{2/3}\cdot 3^{1/2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9526d1e2ba8168d1d558787bdc66421c0517918)
![{\displaystyle f(x,y,z)=2^{2/3}\cdot 3^{1/2}\quad {\mbox{when}}\quad {\frac {x}{y}}={\frac {1}{2}}{\sqrt {\frac {y}{z}}}={\frac {1}{3}}{\sqrt[{3}]{\frac {z}{x}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54067cdd2ecd6283de82387cc8bf466226a8b9ee)
![{\displaystyle (x,y,z)={\biggr (}t,{\sqrt[{3}]{2}}{\sqrt {3}}\,t,{\frac {3{\sqrt {3}}}{2}}\,t{\biggr )}\quad {\mbox{with}}\quad t>0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a8e1d8c753c532b5aaf9a07605a99e901119503)

![{\displaystyle \alpha ={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\geq {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}=\beta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b22e398bf6654d4b119bcc4fb92b596d509ceb4f)






![{\displaystyle {\sqrt[{n}]{\alpha \alpha \cdots \alpha }}=\alpha }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7c4ff626fb396fac26e271b0a3eb067fb846991)






















![{\displaystyle x_{1}={\frac {a_{1}}{\sqrt[{n}]{a_{1}\cdots a_{n}}}},...,x_{n}={\frac {a_{n}}{\sqrt[{n}]{a_{1}\cdots a_{n}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/417da2ea0d3d6e2e39973e3f00e9f5ff2847bf72)
![{\displaystyle {\frac {a_{1}}{\sqrt[{n}]{a_{1}\cdots a_{n}}}}+\cdots +{\frac {a_{n}}{\sqrt[{n}]{a_{1}\cdots a_{n}}}}\geq n,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ec3d5278825ef9a40b8eff6acea290170e34892)
![{\displaystyle {\frac {a_{1}+\cdots +a_{n}}{n}}\geq {\sqrt[{n}]{a_{1}\cdots a_{n}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42f0231cd0d3f2cac2cf48e696e6beb4e883dd82)



![{\displaystyle {\begin{aligned}{\frac {x_{1}+x_{2}+\cdots +x_{2^{k}}}{2^{k}}}&{}={\frac {{\frac {x_{1}+x_{2}+\cdots +x_{2^{k-1}}}{2^{k-1}}}+{\frac {x_{2^{k-1}+1}+x_{2^{k-1}+2}+\cdots +x_{2^{k}}}{2^{k-1}}}}{2}}\\[7pt]&\geq {\frac {{\sqrt[{2^{k-1}}]{x_{1}x_{2}\cdots x_{2^{k-1}}}}+{\sqrt[{2^{k-1}}]{x_{2^{k-1}+1}x_{2^{k-1}+2}\cdots x_{2^{k}}}}}{2}}\\[7pt]&\geq {\sqrt {{\sqrt[{2^{k-1}}]{x_{1}x_{2}\cdots x_{2^{k-1}}}}{\sqrt[{2^{k-1}}]{x_{2^{k-1}+1}x_{2^{k-1}+2}\cdots x_{2^{k}}}}}}\\[7pt]&={\sqrt[{2^{k}}]{x_{1}x_{2}\cdots x_{2^{k}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abd6928892a3005edcf7c6ef1cc3137782eecb08)


![{\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{2^{k}}}{2^{k}}}>{\sqrt[{2^{k}}]{x_{1}x_{2}\cdots x_{2^{k}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d1e238754f3dcedd3256c0d60cee9dcd27aa14a)

![{\displaystyle {\begin{aligned}\alpha &={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\\[6pt]&={\frac {{\frac {m}{n}}\left(x_{1}+x_{2}+\cdots +x_{n}\right)}{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+{\frac {(m-n)}{n}}\left(x_{1}+x_{2}+\cdots +x_{n}\right)}{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+\left(m-n\right)\alpha }{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}+\cdots +x_{m}}{m}}\\[6pt]&\geq {\sqrt[{m}]{x_{1}x_{2}\cdots x_{n}x_{n+1}\cdots x_{m}}}\\[6pt]&={\sqrt[{m}]{x_{1}x_{2}\cdots x_{n}\alpha ^{m-n}}}\,,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b01e1a045936f40f41f67ac4a8dd87df6b7635eb)

![{\displaystyle \alpha \geq {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/111382737971134b4228fd872bb88cc3e697638f)










![{\displaystyle {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}\leq \alpha .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50e75af18e1d4830a475e01e64e3fc821cffdfa9)

































![{\displaystyle {\frac {w_{1}x_{1}+w_{2}x_{2}+\cdots +w_{n}x_{n}}{w}}\geq {\sqrt[{w}]{x_{1}^{w_{1}}x_{2}^{w_{2}}\cdots x_{n}^{w_{n}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a81e30cb6798a0be9b24af48ca1ac493360e08a)

![{\displaystyle {\begin{aligned}\ln {\Bigl (}{\frac {w_{1}x_{1}+\cdots +w_{n}x_{n}}{w}}{\Bigr )}&>{\frac {w_{1}}{w}}\ln x_{1}+\cdots +{\frac {w_{n}}{w}}\ln x_{n}\\&=\ln {\sqrt[{w}]{x_{1}^{w_{1}}x_{2}^{w_{2}}\cdots x_{n}^{w_{n}}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/283ee4b8eb43404edafada3dfe17deec33bda4d3)
![{\displaystyle {\frac {w_{1}x_{1}+\cdots +w_{n}x_{n}}{w}}>{\sqrt[{w}]{x_{1}^{w_{1}}x_{2}^{w_{2}}\cdots x_{n}^{w_{n}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d0ea162b150cfcdea869455ff8ffdf8e1c0987b)























