Initial topology

Ingeneral topologyand related areas ofmathematics,theinitial topology(orinduced topologyorstrong topologyorlimit topologyorprojective topology) on aset$X,$with respect to a family of functions on$X,$is thecoarsest topologyon$X$that makes those functionscontinuous.

Thesubspace topologyandproduct topologyconstructions are both special cases of initial topologies. Indeed, the initial topology construction can be viewed as a generalization of these.

Thedualnotion is thefinal topology,which for a given family of functions mapping to a set$Y$is thefinest topologyon$Y$that makes those functions continuous.

Definition

Given a set$X$and anindexed family$\left(Y_{i}\right)_{i\in I}$oftopological spaceswith functions $$f_{i}:X\to Y_{i},$$ the initial topology$\tau$on$X$is thecoarsest topologyon$X$such that each $$f_{i}:(X,\tau )\to Y_{i}$$ iscontinuous.

Definition in terms of open sets

If$\left(\tau _{i}\right)_{i\in I}$is a family of topologies$X$indexed by$I\neq \varnothing,$then theleast upper boundtopologyof these topologies is the coarsest topology on$X$that is finer than each$\tau _{i}.$This topology always exists and it is equal to thetopology generated by${\textstyle \bigcup \limits _{i\in I}\tau _{i}}.$

If for every$i\in I,$$\sigma _{i}$denotes the topology on$Y_{i},$then$f_{i}^{-1}\left(\sigma _{i}\right)=\left\{f_{i}^{-1}(V):V\in \sigma _{i}\right\}$is a topology on$X$,and theinitial topology of the$Y_{i}$by the mappings$f_{i}$is the least upper bound topology of the$I$-indexed family of topologies$f_{i}^{-1}\left(\sigma _{i}\right)$(for$i\in I$). Explicitly, the initial topology is the collection of open setsgeneratedby all sets of the form$f_{i}^{-1}(U),$where$U$is anopen setin$Y_{i}$for some$i\in I,$under finite intersections and arbitrary unions.

Sets of the form$f_{i}^{-1}(V)$are often calledcylinder sets.If$I$containsexactly one element,then all the open sets of the initial topology$(X,\tau )$are cylinder sets.

Examples

Several topological constructions can be regarded as special cases of the initial topology.

• Thesubspace topologyis the initial topology on the subspace with respect to theinclusion map.
• Theproduct topologyis the initial topology with respect to the family ofprojection maps.
• Theinverse limitof anyinverse systemof spaces and continuous maps is the set-theoretic inverse limit together with the initial topology determined by the canonical morphisms.
• Theweak topologyon alocally convex spaceis the initial topology with respect to thecontinuous linear formsof itsdual space.
• Given afamilyof topologies$\left\{\tau _{i}\right\}$on a fixed set$X$the initial topology on$X$with respect to the functions$\operatorname {id} _{i}:X\to \left(X,\tau _{i}\right)$is thesupremum(or join) of the topologies$\left\{\tau _{i}\right\}$in thelattice of topologieson$X.$That is, the initial topology$\tau$is the topology generated by theunionof the topologies$\left\{\tau _{i}\right\}.$
• A topological space iscompletely regularif and only if it has the initial topology with respect to its family of (bounded) real-valued continuous functions.
• Every topological space$X$has the initial topology with respect to the family of continuous functions from$X$to theSierpiński space.

Properties

Characteristic property

The initial topology on$X$can be characterized by the following characteristic property:
A function$g$from some space$Z$to$X$is continuous if and only if$f_{i}\circ g$is continuous for each$i\in I.$

Characteristic property of the initial topology

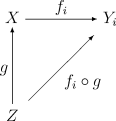
Note that, despite looking quite similar, this is not auniversal property.A categorical description is given below.

Afilter${\mathcal {B}}$on$X$converges toa point$x\in X$if and only if theprefilter$f_{i}({\mathcal {B}})$converges to$f_{i}(x)$for every$i\in I.$

Evaluation

By the universal property of theproduct topology,we know that any family of continuous maps$f_{i}:X\to Y_{i}$determines a unique continuous map $${\begin{alignedat}{4}f:\;&&X&&\;\to \;&\prod _{i}Y_{i}\\[0.3ex]&&x&&\;\mapsto \;&\left(f_{i}(x)\right)_{i\in I}\\\end{alignedat}}$$

This map is known as theevaluation map.

A family of maps$\{f_{i}:X\to Y_{i}\}$is said toseparate pointsin$X$if for all$x\neq y$in$X$there exists some$i$such that$f_{i}(x)\neq f_{i}(y).$The family$\{f_{i}\}$separates points if and only if the associated evaluation map$f$isinjective.

The evaluation map$f$will be atopological embeddingif and only if$X$has the initial topology determined by the maps$\{f_{i}\}$and this family of maps separates points in$X.$

Hausdorffness

If$X$has the initial topology induced by$\left\{f_{i}:X\to Y_{i}\right\}$and if every$Y_{i}$is Hausdorff, then$X$is aHausdorff spaceif and only if these mapsseparate pointson$X.$

Transitivity of the initial topology

If$X$has the initial topology induced by the$I$-indexed family of mappings$\left\{f_{i}:X\to Y_{i}\right\}$and if for every$i\in I,$the topology on$Y_{i}$is the initial topology induced by some$J_{i}$-indexed family of mappings$\left\{g_{j}:Y_{i}\to Z_{j}\right\}$(as$j$ranges over$J_{i}$), then the initial topology on$X$induced by$\left\{f_{i}:X\to Y_{i}\right\}$is equal to the initial topology induced by the${\textstyle \bigcup \limits _{i\in I}J_{i}}$-indexed family of mappings$\left\{g_{j}\circ f_{i}:X\to Z_{j}\right\}$as$i$ranges over$I$and$j$ranges over$J_{i}.$ Several important corollaries of this fact are now given.

In particular, if$S\subseteq X$then the subspace topology that$S$inherits from$X$is equal to the initial topology induced by theinclusion map$S\to X$(defined by$s\mapsto s$). Consequently, if$X$has the initial topology induced by$\left\{f_{i}:X\to Y_{i}\right\}$then the subspace topology that$S$inherits from$X$is equal to the initial topology induced on$S$by the restrictions$\left\{\left.f_{i}\right|_{S}:S\to Y_{i}\right\}$of the$f_{i}$to$S.$

Theproduct topologyon$\prod _{i}Y_{i}$is equal to the initial topology induced by the canonical projections$\operatorname {pr} _{i}:\left(x_{k}\right)_{k\in I}\mapsto x_{i}$as$i$ranges over$I.$ Consequently, the initial topology on$X$induced by$\left\{f_{i}:X\to Y_{i}\right\}$is equal to the inverse image of the product topology on$\prod _{i}Y_{i}$by theevaluation map${\textstyle f:X\to \prod _{i}Y_{i}\,.}$Furthermore, if the maps$\left\{f_{i}\right\}_{i\in I}$separate pointson$X$then the evaluation map is ahomeomorphismonto the subspace$f(X)$of the product space$\prod _{i}Y_{i}.$

Separating points from closed sets

If a space$X$comes equipped with a topology, it is often useful to know whether or not the topology on$X$is the initial topology induced by some family of maps on$X.$This section gives a sufficient (but not necessary) condition.

A family of maps$\left\{f_{i}:X\to Y_{i}\right\}$separates points from closed setsin$X$if for allclosed sets$A$in$X$and all$x\not \in A,$there exists some$i$such that $$f_{i}(x)\notin \operatorname {cl} (f_{i}(A))$$ where$\operatorname {cl}$denotes theclosure operator.

Theorem.A family of continuous maps$\left\{f_{i}:X\to Y_{i}\right\}$separates points from closed sets if and only if the cylinder sets$f_{i}^{-1}(V),$for$V$open in$Y_{i},$form abase for the topologyon$X.$

It follows that whenever$\left\{f_{i}\right\}$separates points from closed sets, the space$X$has the initial topology induced by the maps$\left\{f_{i}\right\}.$The converse fails, since generally the cylinder sets will only form a subbase (and not a base) for the initial topology.

If the space$X$is aT₀space,then any collection of maps$\left\{f_{i}\right\}$that separates points from closed sets in$X$must also separate points. In this case, the evaluation map will be an embedding.

Initial uniform structure

Main article:Uniform space

If$\left({\mathcal {U}}_{i}\right)_{i\in I}$is a family ofuniform structureson$X$indexed by$I\neq \varnothing,$then theleast upper bounduniform structureof$\left({\mathcal {U}}_{i}\right)_{i\in I}$is the coarsest uniform structure on$X$that is finer than each${\mathcal {U}}_{i}.$This uniform always exists and it is equal to thefilteron$X\times X$generated by thefilter subbase${\textstyle \bigcup \limits _{i\in I}{\mathcal {U}}_{i}}.$ If$\tau _{i}$is the topology on$X$induced by the uniform structure${\mathcal {U}}_{i}$then the topology on$X$associated with least upper bound uniform structure is equal to the least upper bound topology of$\left(\tau _{i}\right)_{i\in I}.$

Now suppose that$\left\{f_{i}:X\to Y_{i}\right\}$is a family of maps and for every$i\in I,$let${\mathcal {U}}_{i}$be a uniform structure on$Y_{i}.$Then theinitial uniform structure of the$Y_{i}$by the mappings$f_{i}$is the unique coarsest uniform structure${\mathcal {U}}$on$X$making all$f_{i}:\left(X,{\mathcal {U}}\right)\to \left(Y_{i},{\mathcal {U}}_{i}\right)$uniformly continuous.It is equal to the least upper bound uniform structure of the$I$-indexed family of uniform structures$f_{i}^{-1}\left({\mathcal {U}}_{i}\right)$(for$i\in I$). The topology on$X$induced by${\mathcal {U}}$is the coarsest topology on$X$such that every$f_{i}:X\to Y_{i}$is continuous. The initial uniform structure${\mathcal {U}}$is also equal to the coarsest uniform structure such that the identity mappings$\operatorname {id}:\left(X,{\mathcal {U}}\right)\to \left(X,f_{i}^{-1}\left({\mathcal {U}}_{i}\right)\right)$are uniformly continuous.

Hausdorffness:The topology on$X$induced by the initial uniform structure${\mathcal {U}}$isHausdorffif and only if for whenever$x,y\in X$are distinct ($x\neq y$) then there exists some$i\in I$and some entourage$V_{i}\in {\mathcal {U}}_{i}$of$Y_{i}$such that$\left(f_{i}(x),f_{i}(y)\right)\not \in V_{i}.$ Furthermore, if for every index$i\in I,$the topology on$Y_{i}$induced by${\mathcal {U}}_{i}$is Hausdorff then the topology on$X$induced by the initial uniform structure${\mathcal {U}}$is Hausdorff if and only if the maps$\left\{f_{i}:X\to Y_{i}\right\}$separate pointson$X$(or equivalently, if and only if theevaluation map${\textstyle f:X\to \prod _{i}Y_{i}}$is injective)

Uniform continuity:If${\mathcal {U}}$is the initial uniform structure induced by the mappings$\left\{f_{i}:X\to Y_{i}\right\},$then a function$g$from some uniform space$Z$into$(X,{\mathcal {U}})$isuniformly continuousif and only if$f_{i}\circ g:Z\to Y_{i}$is uniformly continuous for each$i\in I.$

Cauchy filter:Afilter${\mathcal {B}}$on$X$is aCauchy filteron$(X,{\mathcal {U}})$if and only if$f_{i}\left({\mathcal {B}}\right)$is a Cauchy prefilter on$Y_{i}$for every$i\in I.$

Transitivity of the initial uniform structure:If the word "topology" is replaced with "uniform structure" in the statement of "transitivity of the initial topology"given above, then the resulting statement will also be true.

Categorical description

In the language ofcategory theory,the initial topology construction can be described as follows. Let$Y$be thefunctorfrom adiscrete category$J$to thecategory of topological spaces$\mathrm {Top}$which maps$j\mapsto Y_{j}$.Let$U$be the usualforgetful functorfrom$\mathrm {Top}$to$\mathrm {Set}$.The maps$f_{j}:X\to Y_{j}$can then be thought of as aconefrom$X$to$UY.$That is,$(X,f)$is an object of$\mathrm {Cone} (UY):=(\Delta \downarrow {UY})$—thecategory of conesto$UY.$More precisely, this cone$(X,f)$defines a$U$-structured cosink in$\mathrm {Set}.$

The forgetful functor$U:\mathrm {Top} \to \mathrm {Set}$induces a functor${\bar {U}}:\mathrm {Cone} (Y)\to \mathrm {Cone} (UY)$.The characteristic property of the initial topology is equivalent to the statement that there exists auniversal morphismfrom${\bar {U}}$to$(X,f);$that is, aterminal objectin the category$\left({\bar {U}}\downarrow (X,f)\right).$
Explicitly, this consists of an object$I(X,f)$in$\mathrm {Cone} (Y)$together with a morphism$\varepsilon:{\bar {U}}I(X,f)\to (X,f)$such that for any object$(Z,g)$in$\mathrm {Cone} (Y)$and morphism$\varphi:{\bar {U}}(Z,g)\to (X,f)$there exists a unique morphism$\zeta:(Z,g)\to I(X,f)$such that the following diagram commutes:

The assignment$(X,f)\mapsto I(X,f)$placing the initial topology on$X$extends to a functor $I:\mathrm {Cone} (UY)\to \mathrm {Cone} (Y)$ which isright adjointto the forgetful functor${\bar {U}}.$In fact,$I$is a right-inverse to${\bar {U}}$;since${\bar {U}}I$is the identity functor on$\mathrm {Cone} (UY).$

See also

• Final topology– Finest topology making some functions continuous
• Product topology– Topology on Cartesian products of topological spaces
• Quotient space (topology)– Topological space construction
• Subspace topology– Inherited topology

Bibliography

• Bourbaki, Nicolas(1989) [1966].General Topology: Chapters 1–4[Topologie Générale].Éléments de mathématique.Berlin New York: Springer Science & Business Media.ISBN978-3-540-64241-1.OCLC18588129.
• Bourbaki, Nicolas(1989) [1967].General Topology 2: Chapters 5–10[Topologie Générale].Éléments de mathématique.Vol. 4. Berlin New York: Springer Science & Business Media.ISBN978-3-540-64563-4.OCLC246032063.
• Dugundji, James(1966).Topology.Boston: Allyn and Bacon.ISBN978-0-697-06889-7.OCLC395340485.
• Grothendieck, Alexander(1973).Topological Vector Spaces.Translated by Chaljub, Orlando. New York: Gordon and Breach Science Publishers.ISBN978-0-677-30020-7.OCLC886098.
• Willard, Stephen (2004) [1970].General Topology.Mineola, N.Y.:Dover Publications.ISBN978-0-486-43479-7.OCLC115240.
• Willard, Stephen (1970).General Topology.Reading, Massachusetts: Addison-Wesley.ISBN0-486-43479-6.

External links

• Initial topologyatPlanetMath.
• Product topology and subspace topologyatPlanetMath.