Incircle and excircles

"Incircle" redirects here. For incircles of non-triangle polygons, seeTangential quadrilateralandTangential polygon.

Incircle and excircles of a triangle.

Extended sidesof triangle△ABC

Incircle (incenteratI)

Excircles (excenters atJ_A,J_B,J_C)

Internalangle bisectors

External angle bisectors (forming the excentral triangle)

Ingeometry,theincircleorinscribed circleof atriangleis the largestcirclethat can be contained in the triangle; it touches (istangentto) the three sides. The center of the incircle is atriangle centercalled the triangle'sincenter.

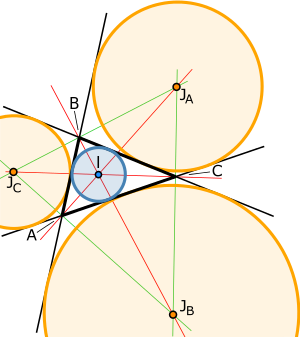
Anexcircleorescribed circleof the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to theextensions of the other two.Every triangle has three distinct excircles, each tangent to one of the triangle's sides.

The center of the incircle, called theincenter,can be found as the intersection of the threeinternalangle bisectors.The center of an excircle is the intersection of the internal bisector of one angle (at vertexA,for example) and theexternalbisectors of the other two. The center of this excircle is called theexcenterrelative to the vertexA,or theexcenterofA.Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the incircle together with the three excircle centers form anorthocentric system.

Incircle and Incenter

See also:Incenter

Suppose$\triangle ABC$has an incircle with radius$r$and center$I$. Let$a$be the length of${\overline {BC}}$,$b$the length of${\overline {AC}}$,and$c$the length of${\overline {AB}}$. Also let$T_{A}$,$T_{B}$,and$T_{C}$be the touchpoints where the incircle touches${\overline {BC}}$,${\overline {AC}}$,and${\overline {AB}}$.

Incenter

The incenter is the point where the internalangle bisectorsof$\angle ABC,\angle BCA,{\text{ and }}\angle BAC$meet.

The distance from vertex$A$to the incenter$I$is: $$d(A,I)=c\,{\frac {\sin {\frac {B}{2}}}{\cos {\frac {C}{2}}}}=b\,{\frac {\sin {\frac {C}{2}}}{\cos {\frac {B}{2}}}}.$$

Trilinear coordinates

Thetrilinear coordinatesfor a point in the triangle is the ratio of all the distances to the triangle sides. Because the incenter is the same distance from all sides of the triangle, the trilinear coordinates for the incenter are $$\ 1:1:1.$$

Barycentric coordinates

Thebarycentric coordinatesfor a point in a triangle give weights such that the point is the weighted average of the triangle vertex positions. Barycentric coordinates for the incenter are given by $$\ a:b:c$$

where$a$,$b$,and$c$are the lengths of the sides of the triangle, or equivalently (using thelaw of sines) by $$\sin A:\sin B:\sin C$$

where$A$,$B$,and$C$are the angles at the three vertices.

Cartesian coordinates

TheCartesian coordinatesof the incenter are a weighted average of the coordinates of the three vertices using the side lengths of the triangle relative to the perimeter (that is, using the barycentric coordinates given above, normalized to sum to unity) as weights. The weights are positive so the incenter lies inside the triangle as stated above. If the three vertices are located at$(x_{a},y_{a})$,$(x_{b},y_{b})$,and$(x_{c},y_{c})$,and the sides opposite these vertices have corresponding lengths$a$,$b$,and$c$,then the incenter is at $$\left({\frac {ax_{a}+bx_{b}+cx_{c}}{a+b+c}},{\frac {ay_{a}+by_{b}+cy_{c}}{a+b+c}}\right)={\frac {a\left(x_{a},y_{a}\right)+b\left(x_{b},y_{b}\right)+c\left(x_{c},y_{c}\right)}{a+b+c}}.$$

Radius

The inradius$r$of the incircle in a triangle with sides of length$a$,$b$,$c$is given by $$r={\sqrt {\frac {(s-a)(s-b)(s-c)}{s}}},$$

where$s={\tfrac {1}{2}}(a+b+c)$is the semiperimeter.

The tangency points of the incircle divide the sides into segments of lengths$s-a$from$A$,$s-b$from$B$,and$s-c$from$C$.

SeeHeron's formula.

Distances to the vertices

Denoting the incenter of$\triangle ABC$as$I$,the distances from the incenter to the vertices combined with the lengths of the triangle sides obey the equation $${\frac {{\overline {IA}}\cdot {\overline {IA}}}{{\overline {CA}}\cdot {\overline {AB}}}}+{\frac {{\overline {IB}}\cdot {\overline {IB}}}{{\overline {AB}}\cdot {\overline {BC}}}}+{\frac {{\overline {IC}}\cdot {\overline {IC}}}{{\overline {BC}}\cdot {\overline {CA}}}}=1.$$

Additionally, $${\overline {IA}}\cdot {\overline {IB}}\cdot {\overline {IC}}=4Rr^{2},$$

where$R$and$r$are the triangle'scircumradiusandinradiusrespectively.

Other properties

The collection of triangle centers may be given the structure of agroupunder coordinate-wise multiplication of trilinear coordinates; in this group, the incenter forms theidentity element.

Incircle and its radius properties

Distances between vertex and nearest touchpoints

The distances from a vertex to the two nearest touchpoints are equal; for example: $$d\left(A,T_{B}\right)=d\left(A,T_{C}\right)={\tfrac {1}{2}}(b+c-a)=s-a.$$

Other properties

If thealtitudesfrom sides of lengths$a$,$b$,and$c$are$h_{a}$,$h_{b}$,and$h_{c}$,then the inradius$r$is one-third of theharmonic meanof these altitudes; that is, $$r={\frac {1}{{\dfrac {1}{h_{a}}}+{\dfrac {1}{h_{b}}}+{\dfrac {1}{h_{c}}}}}.$$

The product of the incircle radius$r$and thecircumcircleradius$R$of a triangle with sides$a$,$b$,and$c$is $$rR={\frac {abc}{2(a+b+c)}}.$$

Some relations among the sides, incircle radius, and circumcircle radius are: $${\begin{aligned}ab+bc+ca&=s^{2}+(4R+r)r,\\a^{2}+b^{2}+c^{2}&=2s^{2}-2(4R+r)r.\end{aligned}}$$

Any line through a triangle that splits both the triangle's area and its perimeter in half goes through the triangle's incenter (the center of its incircle). There are either one, two, or three of these for any given triangle.

Denoting the center of the incircle of$\triangle ABC$as$I$,we have

$${\frac {{\overline {IA}}\cdot {\overline {IA}}}{{\overline {CA}}\cdot {\overline {AB}}}}+{\frac {{\overline {IB}}\cdot {\overline {IB}}}{{\overline {AB}}\cdot {\overline {BC}}}}+{\frac {{\overline {IC}}\cdot {\overline {IC}}}{{\overline {BC}}\cdot {\overline {CA}}}}=1$$

and $${\overline {IA}}\cdot {\overline {IB}}\cdot {\overline {IC}}=4Rr^{2}.$$

The incircle radius is no greater than one-ninth the sum of the altitudes.

The squared distance from the incenter$I$to the circumcenter$O$is given by $${\overline {OI}}^{2}=R(R-2r)={\frac {a\,b\,c\,}{a+b+c}}\left[{\frac {a\,b\,c\,}{(a+b-c)\,(a-b+c)\,(-a+b+c)}}-1\right]$$

and the distance from the incenter to the center$N$of thenine point circleis $${\overline {IN}}={\tfrac {1}{2}}(R-2r)<{\tfrac {1}{2}}R.$$

The incenter lies in themedial triangle(whose vertices are the midpoints of the sides).

Relation to area of the triangle

"Inradius" redirects here. For the three-dimensional equivalent, seeInscribed sphere.

The radius of the incircle is related to theareaof the triangle.The ratio of the area of the incircle to the area of the triangle is less than or equal to $\pi {\big /}3{\sqrt {3}}$, with equality holding only forequilateral triangles.

Suppose $\triangle ABC$ has an incircle with radius$r$and center$I$.Let$a$be the length of${\overline {BC}}$,$b$the length of${\overline {AC}}$,and$c$the length of${\overline {AB}}$.Now, the incircle is tangent to${\overline {AB}}$at some point$T_{C}$,and so $\angle AT_{C}I$ is right. Thus, the radius$T_{C}I$is analtitudeof $\triangle IAB$. Therefore, $\triangle IAB$ has base length$c$and height$r$,and so has area ${\tfrac {1}{2}}cr$. Similarly, $\triangle IAC$ has area ${\tfrac {1}{2}}br$ and $\triangle IBC$ has area ${\tfrac {1}{2}}ar$. Since these three triangles decompose $\triangle ABC$,we see that the area $\Delta {\text{ of }}\triangle ABC$ is: $$\Delta ={\tfrac {1}{2}}(a+b+c)r=sr,$$and$r={\frac {\Delta }{s}},$

where$\Delta$is the area of$\triangle ABC$and$s={\tfrac {1}{2}}(a+b+c)$is itssemiperimeter.

For an alternative formula, consider$\triangle IT_{C}A$.This is a right-angled triangle with one side equal to$r$and the other side equal to$r\cot {\tfrac {A}{2}}$.The same is true for$\triangle IB'A$.The large triangle is composed of six such triangles and the total area is: $$\Delta =r^{2}\left(\cot {\tfrac {A}{2}}+\cot {\tfrac {B}{2}}+\cot {\tfrac {C}{2}}\right).$$

Gergonne triangle and point

Triangle△ABC

Incircle (incenteratI)

Contact triangle△T_AT_BT_C

Lines between opposite vertices of△ABCand△T_AT_BT_C(concur at Gergonne pointG_e)

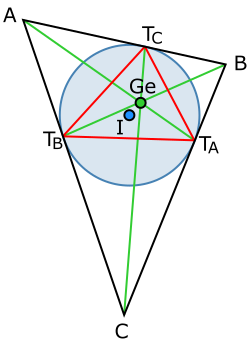
TheGergonne triangle(of$\triangle ABC$) is defined by the three touchpoints of the incircle on the three sides. The touchpoint opposite$A$is denoted$T_{A}$,etc.

This Gergonne triangle,$\triangle T_{A}T_{B}T_{C}$,is also known as thecontact triangleorintouch triangleof$\triangle ABC$.Its area is $$K_{T}=K{\frac {2r^{2}s}{abc}}$$

where$K$,$r$,and$s$are the area, radius of theincircle,and semiperimeter of the original triangle, and$a$,$b$,and$c$are the side lengths of the original triangle. This is the same area as that of theextouch triangle.

The three lines$AT_{A}$,$BT_{B}$and$CT_{C}$intersect in a single point called theGergonne point,denoted as$G_{e}$(ortriangle centerX₇). The Gergonne point lies in the openorthocentroidal diskpunctured at its own center, and can be any point therein.

The Gergonne point of a triangle has a number of properties, including that it is thesymmedian pointof the Gergonne triangle.

Trilinear coordinatesfor the vertices of the intouch triangle are given by $${\begin{array}{ccccccc}T_{A}&=&0&:&\sec ^{2}{\frac {B}{2}}&:&\sec ^{2}{\frac {C}{2}}\\[2pt]T_{B}&=&\sec ^{2}{\frac {A}{2}}&:&0&:&\sec ^{2}{\frac {C}{2}}\\[2pt]T_{C}&=&\sec ^{2}{\frac {A}{2}}&:&\sec ^{2}{\frac {B}{2}}&:&0.\end{array}}$$

Trilinear coordinates for the Gergonne point are given by $$\sec ^{2}{\tfrac {A}{2}}:\sec ^{2}{\tfrac {B}{2}}:\sec ^{2}{\tfrac {C}{2}},$$

or, equivalently, by theLaw of Sines, $${\frac {bc}{b+c-a}}:{\frac {ca}{c+a-b}}:{\frac {ab}{a+b-c}}.$$

Excircles and excenters

Extended sidesof△ABC

Incircle (incenteratI)

Excircles (excenters atJ_A,J_B,J_C)

Internalangle bisectors

External angle bisectors (forming the excentral triangle)

Anexcircleorescribed circleof the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to theextensions of the other two.Every triangle has three distinct excircles, each tangent to one of the triangle's sides.

The center of an excircle is the intersection of the internal bisector of one angle (at vertex$A$,for example) and theexternalbisectors of the other two. The center of this excircle is called theexcenterrelative to the vertex$A$,or theexcenterof$A$.Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the incircle together with the three excircle centers form anorthocentric system.

Trilinear coordinates of excenters

While theincenterof$\triangle ABC$hastrilinear coordinates$1:1:1$,the excenters have trilinears $${\begin{array}{rrcrcr}J_{A}=&-1&:&1&:&1\\J_{B}=&1&:&-1&:&1\\J_{C}=&1&:&1&:&-1\end{array}}$$

Exradii

The radii of the excircles are called theexradii.

The exradius of the excircle opposite$A$(so touching$BC$,centered at$J_{A}$) is $$r_{a}={\frac {rs}{s-a}}={\sqrt {\frac {s(s-b)(s-c)}{s-a}}},$$where$s={\tfrac {1}{2}}(a+b+c).$

SeeHeron's formula.

Derivation of exradii formula

Source:

Let the excircle at side$AB$touch at side$AC$extended at$G$,and let this excircle's radius be$r_{c}$and its center be$J_{c}$.Then$J_{c}G$is an altitude of$\triangle ACJ_{c}$,so$\triangle ACJ_{c}$has area${\tfrac {1}{2}}br_{c}$.By a similar argument,$\triangle BCJ_{c}$has area${\tfrac {1}{2}}ar_{c}$and$\triangle ABJ_{c}$has area${\tfrac {1}{2}}cr_{c}$.Thus the area$\Delta$of triangle$\triangle ABC$is $$\Delta ={\tfrac {1}{2}}(a+b-c)r_{c}=(s-c)r_{c}$$.

So, by symmetry, denoting$r$as the radius of the incircle, $$\Delta =sr=(s-a)r_{a}=(s-b)r_{b}=(s-c)r_{c}$$.

By theLaw of Cosines,we have $$\cos A={\frac {b^{2}+c^{2}-a^{2}}{2bc}}$$

Combining this with the identity$\sin ^{2}\!A+\cos ^{2}\!A=1$,we have $$\sin A={\frac {\sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2b^{2}c^{2}+2a^{2}c^{2}}}{2bc}}$$

But$\Delta ={\tfrac {1}{2}}bc\sin A$,and so $${\begin{aligned}\Delta &={\tfrac {1}{4}}{\sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2b^{2}c^{2}+2a^{2}c^{2}}}\\[5mu]&={\tfrac {1}{4}}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\\[5mu]&={\sqrt {s(s-a)(s-b)(s-c)}},\end{aligned}}$$

which isHeron's formula.

Combining this with$sr=\Delta$,we have $$r^{2}={\frac {\Delta ^{2}}{s^{2}}}={\frac {(s-a)(s-b)(s-c)}{s}}.$$

Similarly,$(s-a)r_{a}=\Delta$gives $${\begin{aligned}&r_{a}^{2}={\frac {s(s-b)(s-c)}{s-a}}\\[4pt]&\implies r_{a}={\sqrt {\frac {s(s-b)(s-c)}{s-a}}}.\end{aligned}}$$

Other properties

From the formulas above one can see that the excircles are always larger than the incircle and that the largest excircle is the one tangent to the longest side and the smallest excircle is tangent to the shortest side. Further, combining these formulas yields: $$\Delta ={\sqrt {rr_{a}r_{b}r_{c}}}.$$

Other excircle properties

The circularhullof the excircles is internally tangent to each of the excircles and is thus anApollonius circle.The radius of this Apollonius circle is${\tfrac {r^{2}+s^{2}}{4r}}$where$r$is the incircle radius and$s$is the semiperimeter of the triangle.

The following relations hold among the inradius$r$,the circumradius$R$,the semiperimeter$s$,and the excircle radii$r_{a}$,$r_{b}$,$r_{c}$: $${\begin{aligned}r_{a}+r_{b}+r_{c}&=4R+r,\\r_{a}r_{b}+r_{b}r_{c}+r_{c}r_{a}&=s^{2},\\r_{a}^{2}+r_{b}^{2}+r_{c}^{2}&=\left(4R+r\right)^{2}-2s^{2}.\end{aligned}}$$

The circle through the centers of the three excircles has radius$2R$.

If$H$is theorthocenterof$\triangle ABC$,then $${\begin{aligned}r_{a}+r_{b}+r_{c}+r&={\overline {AH}}+{\overline {BH}}+{\overline {CH}}+2R,\\r_{a}^{2}+r_{b}^{2}+r_{c}^{2}+r^{2}&={\overline {AH}}^{2}+{\overline {BH}}^{2}+{\overline {CH}}^{2}+(2R)^{2}.\end{aligned}}$$

Nagel triangle and Nagel point

Main article:Extouch triangle

Extended sidesof triangle△ABC

Excircles of△ABC(tangent atT_A.T_B,T_C)

Nagel/Extouch triangle△T_AT_BT_C

Splitters:lines connecting opposite vertices of△ABCand△T_AT_BT_C(concur atNagel pointN)

TheNagel triangleorextouch triangleof$\triangle ABC$is denoted by the vertices$T_{A}$,$T_{B}$,and$T_{C}$that are the three points where the excircles touch the reference$\triangle ABC$and where$T_{A}$is opposite of$A$,etc. This$\triangle T_{A}T_{B}T_{C}$is also known as theextouch triangleof$\triangle ABC$.Thecircumcircleof the extouch$\triangle T_{A}T_{B}T_{C}$is called theMandart circle.

The three line segments${\overline {AT_{A}}}$,${\overline {BT_{B}}}$and${\overline {CT_{C}}}$are called thesplittersof the triangle; they each bisect the perimeter of the triangle, $${\overline {AB}}+{\overline {BT_{A}}}={\overline {AC}}+{\overline {CT_{A}}}={\frac {1}{2}}\left({\overline {AB}}+{\overline {BC}}+{\overline {AC}}\right).$$

The splitters intersect in a single point, the triangle'sNagel point$N_{a}$(ortriangle centerX₈).

Trilinear coordinates for the vertices of the extouch triangle are given by $${\begin{array}{ccccccc}T_{A}&=&0&:&\csc ^{2}{\frac {B}{2}}&:&\csc ^{2}{\frac {C}{2}}\\[2pt]T_{B}&=&\csc ^{2}{\frac {A}{2}}&:&0&:&\csc ^{2}{\frac {C}{2}}\\[2pt]T_{C}&=&\csc ^{2}{\frac {A}{2}}&:&\csc ^{2}{\frac {B}{2}}&:&0\end{array}}$$

Trilinear coordinates for the Nagel point are given by $$\csc ^{2}{\tfrac {A}{2}}:\csc ^{2}{\tfrac {B}{2}}:\csc ^{2}{\tfrac {C}{2}},$$

or, equivalently, by theLaw of Sines, $${\frac {b+c-a}{a}}:{\frac {c+a-b}{b}}:{\frac {a+b-c}{c}}.$$

The Nagel point is theisotomic conjugateof the Gergonne point.

Related constructions

Nine-point circle and Feuerbach point

Main article:Nine-point circle

The nine-point circle is tangent to the incircle and excircles

Ingeometry,thenine-point circleis acirclethat can be constructed for any giventriangle.It is so named because it passes through nine significantconcyclic pointsdefined from the triangle. These ninepointsare:

• Themidpointof each side of the triangle
• Thefootof eachaltitude
• The midpoint of theline segmentfrom eachvertexof the triangle to theorthocenter(where the three altitudes meet; these line segments lie on their respective altitudes).

In 1822, Karl Feuerbach discovered that any triangle's nine-point circle is externallytangentto that triangle's threeexcirclesand internally tangent to itsincircle;this result is known asFeuerbach's theorem.He proved that:

... the circle which passes through the feet of the altitudes of a triangle is tangent to all four circles which in turn are tangent to the three sides of the triangle... (Feuerbach 1822)

Thetriangle centerat which the incircle and the nine-point circle touch is called theFeuerbach point.

Incentral and excentral triangles

The points of intersection of the interior angle bisectors of$\triangle ABC$with the segments$BC$,$CA$,and$AB$are the vertices of theincentral triangle.Trilinear coordinates for the vertices of the incentral triangle$\triangle A'B'C'$are given by $${\begin{array}{ccccccc}A'&=&0&:&1&:&1\\[2pt]B'&=&1&:&0&:&1\\[2pt]C'&=&1&:&1&:&0\end{array}}$$

Theexcentral triangleof a reference triangle has vertices at the centers of the reference triangle's excircles. Its sides are on the external angle bisectors of the reference triangle (see figure attop of page). Trilinear coordinates for the vertices of the excentral triangle$\triangle A'B'C'$are given by $${\begin{array}{ccrcrcr}A'&=&-1&:&1&:&1\\[2pt]B'&=&1&:&-1&:&1\\[2pt]C'&=&1&:&1&:&-1\end{array}}$$

Equations for four circles

Let$x:y:z$be a variable point intrilinear coordinates,and let$u=\cos ^{2}\left(A/2\right)$,$v=\cos ^{2}\left(B/2\right)$,$w=\cos ^{2}\left(C/2\right)$.The four circles described above are given equivalently by either of the two given equations:

• Incircle:$${\begin{aligned}u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}-2vwyz-2wuzx-2uvxy&=0\\[4pt]{\textstyle \pm {\sqrt {x}}\cos {\tfrac {A}{2}}\pm {\sqrt {y{\vphantom {t}}}}\cos {\tfrac {B}{2}}\pm {\sqrt {z}}\cos {\tfrac {C}{2}}}&=0\end{aligned}}$$
• $A$-excircle:$${\begin{aligned}u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}-2vwyz+2wuzx+2uvxy&=0\\[4pt]{\textstyle \pm {\sqrt {-x}}\cos {\tfrac {A}{2}}\pm {\sqrt {y{\vphantom {t}}}}\cos {\tfrac {B}{2}}\pm {\sqrt {z}}\cos {\tfrac {C}{2}}}&=0\end{aligned}}$$
• $B$-excircle:$${\begin{aligned}u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}+2vwyz-2wuzx+2uvxy&=0\\[4pt]{\textstyle \pm {\sqrt {x}}\cos {\tfrac {A}{2}}\pm {\sqrt {-y{\vphantom {t}}}}\cos {\tfrac {B}{2}}\pm {\sqrt {z}}\cos {\tfrac {C}{2}}}&=0\end{aligned}}$$
• $C$-excircle:$${\begin{aligned}u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}+2vwyz+2wuzx-2uvxy&=0\\[4pt]{\textstyle \pm {\sqrt {x}}\cos {\tfrac {A}{2}}\pm {\sqrt {y{\vphantom {t}}}}\cos {\tfrac {B}{2}}\pm {\sqrt {-z}}\cos {\tfrac {C}{2}}}&=0\end{aligned}}$$

Euler's theorem

Euler's theoremstates that in a triangle: $$(R-r)^{2}=d^{2}+r^{2},$$

where$R$and$r$are the circumradius and inradius respectively, and$d$is the distance between thecircumcenterand the incenter.

For excircles the equation is similar: $$\left(R+r_{\text{ex}}\right)^{2}=d_{\text{ex}}^{2}+r_{\text{ex}}^{2},$$

where$r_{\text{ex}}$is the radius of one of the excircles, and$d_{\text{ex}}$is the distance between the circumcenter and that excircle's center.

Generalization to other polygons

Some (but not all)quadrilateralshave an incircle. These are calledtangential quadrilaterals.Among their many properties perhaps the most important is that their two pairs of opposite sides have equal sums. This is called thePitot theorem.

More generally, a polygon with any number of sides that has an inscribed circle (that is, one that is tangent to each side) is called atangential polygon.

See also

• Circumgon– Geometric figure which circumscribes a circle
• Circumcircle– Circle that passes through the vertices of a triangle
• Ex-tangential quadrilateral– Convex 4-sided polygon whose sidelines are all tangent to an outside circle
• Harcourt's theorem– Area of a triangle from its sides and vertex distances to any line tangent to its incircle
• Circumconic and inconic– Conic section that passes through the vertices of a triangle or is tangent to its sides
• Inscribed sphere– Sphere tangent to every face of a polyhedron
• Power of a point– Relative distance of a point from a circle
• Steiner inellipse– Unique ellipse tangent to all 3 midpoints of a given triangle's sides
• Tangential quadrilateral– Polygon whose four sides all touch a circle
• Triangle conic
• Incenter–excenter lemma– A statement about properties of inscribed and circumscribed circles

References

• Altshiller-Court, Nathan (1925),College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle(2nd ed.), New York:Barnes & Noble,LCCN52013504
• Johnson, Roger A. (1929),"X. Inscribed and Escribed Circles",Modern Geometry,Houghton Mifflin, pp. 182–194
• Josefsson, Martin (2011),"More characterizations of tangential quadrilaterals"(PDF),Forum Geometricorum,11:65–82,MR2877281,archived fromthe original(PDF)on 2016-03-04,retrieved2023-03-14
• Kay, David C. (1969),College Geometry,New York:Holt, Rinehart and Winston,LCCN69012075
• Kimberling, Clark (1998). "Triangle Centers and Central Triangles".Congressus Numerantium(129): i–xxv, 1–295.
• Kiss, Sándor (2006). "The Orthic-of-Intouch and Intouch-of-Orthic Triangles".Forum Geometricorum(6): 171–177.

External links

• Derivation of formula for radius of incircle of a triangle
• Weisstein, Eric W."Incircle".MathWorld.

Interactive

• Triangle incenterTriangle incircleIncircle of a regular polygonWith interactive animations
• Constructing a triangle's incenter / incircle with compass and straightedgeAn interactive animated demonstration
• Equal Incircles Theorematcut-the-knot
• Five Incircles Theorematcut-the-knot
• Pairs of Incircles in a Quadrilateralatcut-the-knot
• An interactive Java applet for the incenter