Integral

This article is about the concept of definite integrals in calculus. For the indefinite integral, seeantiderivative.For the set of numbers, seeinteger.For other uses, seeIntegral (disambiguation).

"Area under the curve" redirects here. For the pharmacology integral, seeArea under the curve (pharmacokinetics).For the statistics concept, seeReceiver operating characteristic § Area under the curve.

A definite integral of a function can be represented as thesigned areaof the region bounded by its graph and the horizontal axis; in the above graph as an example, the integral of$f(x)$is the yellow (−) area subtracted from the blue (+) area

Inmathematics,anintegralis the continuous analog of asum,which is used to calculateareas,volumes,and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations ofcalculus,the other beingdifferentiation.Integration was initially used to solve problems in mathematics andphysics,such as finding thearea under a curve,or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter.

Adefinite integralcomputes thesigned areaof the region in the plane that is bounded by thegraphof a givenfunctionbetween two points in thereal line.Conventionally, areas above the horizontalaxisof the plane are positive while areas below are negative. Integrals also refer to the concept of anantiderivative,a function whosederivativeis the given function; in this case, they are also calledindefinite integrals.Thefundamental theorem of calculusrelates definite integration to differentiation and provides a method to compute the definite integral of a function when its antiderivative is known; differentiation and integration areinverseoperations.

Although methods of calculating areas and volumes dated fromancient Greek mathematics,the principles of integration were formulated independently byIsaac NewtonandGottfried Wilhelm Leibnizin the late 17th century, who thought of the area under a curve as an infinite sum of rectangles ofinfinitesimalwidth.Bernhard Riemannlater gave a rigorous definition of integrals, which is based on a limiting procedure that approximates the area of acurvilinearregion by breaking the region into infinitesimally thin vertical slabs. In the early 20th century,Henri Lebesguegeneralized Riemann's formulation by introducing what is now referred to as theLebesgue integral;it is more general than Riemann's in the sense that a wider class of functions are Lebesgue-integrable.

Integrals may be generalized depending on the type of the function as well as thedomainover which the integration is performed. For example, aline integralis defined for functions of two or more variables, and theintervalof integration is replaced by a curve connecting two points in space. In asurface integral,the curve is replaced by a piece of asurfaceinthree-dimensional space.

History

See also:History of calculus

Pre-calculus integration

The first documented systematic technique capable of determining integrals is themethod of exhaustionof theancient GreekastronomerEudoxusand philosopherDemocritus(ca.370 BC), which sought to find areas and volumes by breaking them up into an infinite number of divisions for which the area or volume was known.This method was further developed and employed byArchimedesin the 3rd century BC and used to calculate thearea of a circle,thesurface areaandvolumeof asphere,area of anellipse,the area under aparabola,the volume of a segment of aparaboloidof revolution, the volume of a segment of ahyperboloidof revolution, and the area of aspiral.

A similar method was independently developed inChinaaround the 3rd century AD byLiu Hui,who used it to find the area of the circle. This method was later used in the 5th century by Chinese father-and-son mathematiciansZu ChongzhiandZu Gengto find the volume of a sphere.

In the Middle East, Hasan Ibn al-Haytham, Latinized asAlhazen(c. 965– c. 1040AD) derived a formula for the sum offourth powers.Alhazen determined the equations to calculate the area enclosed by the curve represented by$y=x^{k}$(which translates to the integral$\int x^{k}\,dx$in contemporary notation), for any given non-negative integer value of$k$.He used the results to carry out what would now be called an integration of this function, where the formulae for the sums of integral squares and fourth powers allowed him to calculate the volume of aparaboloid.

The next significant advances in integral calculus did not begin to appear until the 17th century. At this time, the work ofCavalieriwith hismethod of indivisibles,and work byFermat,began to lay the foundations of modern calculus,with Cavalieri computing the integrals ofxⁿup to degreen= 9inCavalieri's quadrature formula.The casen= −1 required the invention of afunction,thehyperbolic logarithm,achieved byquadratureof thehyperbolain 1647.

Further steps were made in the early 17th century byBarrowandTorricelli,who provided the first hints of a connection between integration anddifferentiation.Barrow provided the first proof of thefundamental theorem of calculus.Wallisgeneralized Cavalieri's method, computing integrals ofxto a general power, including negative powers and fractional powers.

Leibniz and Newton

The major advance in integration came in the 17th century with the independent discovery of thefundamental theorem of calculusbyLeibnizandNewton.The theorem demonstrates a connection between integration and differentiation. This connection, combined with the comparative ease of differentiation, can be exploited to calculate integrals. In particular, the fundamental theorem of calculus allows one to solve a much broader class of problems. Equal in importance is the comprehensive mathematical framework that both Leibniz and Newton developed. Given the name infinitesimal calculus, it allowed for precise analysis of functions with continuous domains. This framework eventually became moderncalculus,whose notation for integrals is drawn directly from the work of Leibniz.

Formalization

While Newton and Leibniz provided a systematic approach to integration, their work lacked a degree ofrigour.Bishop Berkeleymemorably attacked the vanishing increments used by Newton, calling them "ghosts of departed quantities".Calculus acquired a firmer footing with the development oflimits.Integration was first rigorously formalized, using limits, byRiemann.Although all boundedpiecewisecontinuous functions are Riemann-integrable on a bounded interval, subsequently more general functions were considered—particularly in the context ofFourier analysis—to which Riemann's definition does not apply, andLebesgueformulated adifferent definition of integral,founded inmeasure theory(a subfield ofreal analysis). Other definitions of integral, extending Riemann's and Lebesgue's approaches, were proposed. These approaches based on the real number system are the ones most common today, but alternative approaches exist, such as a definition of integral as thestandard partof an infinite Riemann sum, based on thehyperreal numbersystem.

Historical notation

The notation for the indefinite integral was introduced byGottfried Wilhelm Leibnizin 1675.He adapted theintegral symbol,∫,from the letterſ(long s), standing forsumma(written asſumma;Latin for "sum" or "total" ). The modern notation for the definite integral, with limits above and below the integral sign, was first used byJoseph FourierinMémoiresof the French Academy around 1819–1820, reprinted in his book of 1822.

Isaac Newtonused a small vertical bar above a variable to indicate integration, or placed the variable inside a box. The vertical bar was easily confused with.xorx′,which are used to indicate differentiation, and the box notation was difficult for printers to reproduce, so these notations were not widely adopted.

First use of the term

The term was first printed in Latin byJacob Bernoulliin 1690: "Ergo et horum Integralia aequantur".

Terminology and notation

In general, the integral of areal-valued functionf(x)with respect to a real variablexon an interval[a,b]is written as

$\int _{a}^{b}f(x)\,dx.$

The integral sign∫represents integration. The symboldx,called thedifferentialof the variablex,indicates that the variable of integration isx.The functionf(x)is called theintegrand,the pointsaandbare called the limits (or bounds) of integration, and the integral is said to be over the interval[a,b],called the interval of integration. A function is said to beintegrableif its integral over its domain is finite. If limits are specified, the integral is called a definite integral.

When the limits are omitted, as in

$\int f(x)\,dx,$

the integral is called an indefinite integral, which represents a class of functions (theantiderivative) whose derivative is the integrand.Thefundamental theorem of calculusrelates the evaluation of definite integrals to indefinite integrals. There are several extensions of the notation for integrals to encompass integration on unbounded domains and/or in multiple dimensions (see later sections of this article).

In advanced settings, it is not uncommon to leave outdxwhen only the simple Riemann integral is being used, or the exact type of integral is immaterial. For instance, one might write${\textstyle \int _{a}^{b}(c_{1}f+c_{2}g)=c_{1}\int _{a}^{b}f+c_{2}\int _{a}^{b}g}$to express the linearity of the integral, a property shared by the Riemann integral and all generalizations thereof.

Interpretations

Approximations to integral of√xfrom 0 to 1, with 5 yellow right endpoint partitions and 10 green left endpoint partitions

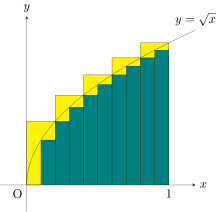
Integrals appear in many practical situations. For instance, from the length, width and depth of a swimming pool which is rectangular with a flat bottom, one can determine the volume of water it can contain, the area of its surface, and the length of its edge. But if it is oval with a rounded bottom, integrals are required to find exact and rigorous values for these quantities. In each case, one may divide the sought quantity into infinitely manyinfinitesimalpieces, then sum the pieces to achieve an accurate approximation.

As another example, to find the area of the region bounded by the graph of the functionf(x) =${\textstyle {\sqrt {x}}}$betweenx= 0andx= 1,one can divide the interval into five pieces (0, 1/5, 2/5,..., 1), then construct rectangles using the right end height of each piece (thus√0,√1/5,√2/5,...,√1) and sum their areas to get the approximation

$\textstyle {\sqrt {\frac {1}{5}}}\left({\frac {1}{5}}-0\right)+{\sqrt {\frac {2}{5}}}\left({\frac {2}{5}}-{\frac {1}{5}}\right)+\cdots +{\sqrt {\frac {5}{5}}}\left({\frac {5}{5}}-{\frac {4}{5}}\right)\approx 0.7497,$

which is larger than the exact value. Alternatively, when replacing these subintervals by ones with the left end height of each piece, the approximation one gets is too low: with twelve such subintervals the approximated area is only 0.6203. However, when the number of pieces increases to infinity, it will reach a limit which is the exact value of the area sought (in this case,2/3). One writes

$\int _{0}^{1}{\sqrt {x}}\,dx={\frac {2}{3}},$

which means2/3is the result of a weighted sum of function values,√x,multiplied by the infinitesimal step widths, denoted bydx,on the interval[0, 1].

Darboux sums

Darboux upper sums of the functiony=x²

Darboux lower sums of the functiony=x²

Formal definitions

Riemann sums converging

There are many ways of formally defining an integral, not all of which are equivalent. The differences exist mostly to deal with differing special cases which may not be integrable under other definitions, but are also occasionally for pedagogical reasons. The most commonly used definitions are Riemann integrals and Lebesgue integrals.

Riemann integral

Main article:Riemann integral

The Riemann integral is defined in terms ofRiemann sumsof functions with respect totagged partitionsof an interval.A tagged partition of aclosed interval[a,b]on the real line is a finite sequence

$a=x_{0}\leq t_{1}\leq x_{1}\leq t_{2}\leq x_{2}\leq \cdots \leq x_{n-1}\leq t_{n}\leq x_{n}=b.\,\!$

This partitions the interval[a,b]intonsub-intervals[x_i−1,x_i]indexed byi,each of which is "tagged" with a specific pointt_i∈ [x_i−1,x_i].ARiemann sumof a functionfwith respect to such a tagged partition is defined as

$\sum _{i=1}^{n}f(t_{i})\,\Delta _{i};$

thus each term of the sum is the area of a rectangle with height equal to the function value at the chosen point of the given sub-interval, and width the same as the width of sub-interval,Δ_i=x_i−x_i−1.Themeshof such a tagged partition is the width of the largest sub-interval formed by the partition,max_i=1...nΔ_i.TheRiemann integralof a functionfover the interval[a,b]is equal toSif:

For all$\varepsilon >0$there exists$\delta >0$such that, for any tagged partition$[a,b]$with mesh less than$\delta$,

$\left|S-\sum _{i=1}^{n}f(t_{i})\,\Delta _{i}\right|<\varepsilon.$

When the chosen tags are the maximum (respectively, minimum) value of the function in each interval, the Riemann sum becomes an upper (respectively, lower)Darboux sum,suggesting the close connection between the Riemann integral and theDarboux integral.

Lebesgue integral

Main article:Lebesgue integration

Lebesgue integration

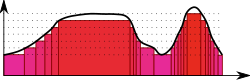
It is often of interest, both in theory and applications, to be able to pass to the limit under the integral. For instance, a sequence of functions can frequently be constructed that approximate, in a suitable sense, the solution to a problem. Then the integral of the solution function should be the limit of the integrals of the approximations. However, many functions that can be obtained as limits are not Riemann-integrable, and so such limit theorems do not hold with the Riemann integral. Therefore, it is of great importance to have a definition of the integral that allows a wider class of functions to be integrated.

Such an integral is the Lebesgue integral, that exploits the following fact to enlarge the class of integrable functions: if the values of a function are rearranged over the domain, the integral of a function should remain the same. ThusHenri Lebesgueintroduced the integral bearing his name, explaining this integral thus in a letter toPaul Montel:

I have to pay a certain sum, which I have collected in my pocket. I take the bills and coins out of my pocket and give them to the creditor in the order I find them until I have reached the total sum. This is the Riemann integral. But I can proceed differently. After I have taken all the money out of my pocket I order the bills and coins according to identical values and then I pay the several heaps one after the other to the creditor. This is my integral.

As Folland puts it, "To compute the Riemann integral off,one partitions the domain[a,b]into subintervals ", while in the Lebesgue integral," one is in effect partitioning the range off".The definition of the Lebesgue integral thus begins with ameasure,μ. In the simplest case, theLebesgue measureμ(A)of an intervalA= [a,b]is its width,b−a,so that the Lebesgue integral agrees with the (proper) Riemann integral when both exist.In more complicated cases, the sets being measured can be highly fragmented, with no continuity and no resemblance to intervals.

Using the "partitioning the range off"philosophy, the integral of a non-negative functionf:R→Rshould be the sum overtof the areas between a thin horizontal strip betweeny=tandy=t+dt.This area is justμ{x:f(x) >t} dt.Letf^∗(t) =μ{x:f(x) >t}.The Lebesgue integral offis then defined by

$\int f=\int _{0}^{\infty }f^{*}(t)\,dt$

where the integral on the right is an ordinary improper Riemann integral (f^∗is a strictly decreasing positive function, and therefore has awell-definedimproper Riemann integral).For a suitable class of functions (themeasurable functions) this defines the Lebesgue integral.

A general measurable functionfis Lebesgue-integrable if the sum of the absolute values of the areas of the regions between the graph offand thex-axis is finite:

$\int _{E}|f|\,d\mu <+\infty.$

In that case, the integral is, as in the Riemannian case, the difference between the area above thex-axis and the area below thex-axis:

$\int _{E}f\,d\mu =\int _{E}f^{+}\,d\mu -\int _{E}f^{-}\,d\mu$

where

${\begin{alignedat}{3}&f^{+}(x)&&{}={}\max\{f(x),0\}&&{}={}{\begin{cases}f(x),&{\text{if }}f(x)>0,\\0,&{\text{otherwise,}}\end{cases}}\\&f^{-}(x)&&{}={}\max\{-f(x),0\}&&{}={}{\begin{cases}-f(x),&{\text{if }}f(x)<0,\\0,&{\text{otherwise.}}\end{cases}}\end{alignedat}}$

Other integrals

Although the Riemann and Lebesgue integrals are the most widely used definitions of the integral, a number of others exist, including:

• TheDarboux integral,which is defined by Darboux sums (restricted Riemann sums) yet is equivalent to theRiemann integral.A function is Darboux-integrable if and only if it is Riemann-integrable. Darboux integrals have the advantage of being easier to define than Riemann integrals.
• TheRiemann–Stieltjes integral,an extension of the Riemann integral which integrates with respect to a function as opposed to a variable.
• TheLebesgue–Stieltjes integral,further developed byJohann Radon,which generalizes both the Riemann–Stieltjes and Lebesgue integrals.
• TheDaniell integral,which subsumes the Lebesgue integral andLebesgue–Stieltjes integralwithout depending onmeasures.
• TheHaar integral,used for integration on locally compact topological groups, introduced byAlfréd Haarin 1933.
• TheHenstock–Kurzweil integral,variously defined byArnaud Denjoy,Oskar Perron,and (most elegantly, as the gauge integral)Jaroslav Kurzweil,and developed byRalph Henstock.
• TheKhinchin integral,named afterAleksandr Khinchin.
• TheItô integralandStratonovich integral,which define integration with respect tosemimartingalessuch asBrownian motion.
• TheYoung integral,which is a kind of Riemann–Stieltjes integral with respect to certain functions ofunbounded variation.
• Therough pathintegral, which is defined for functions equipped with some additional "rough path" structure and generalizes stochastic integration against bothsemimartingalesand processes such as thefractional Brownian motion.
• TheChoquet integral,a subadditive or superadditive integral created by the French mathematician Gustave Choquet in 1953.
• TheBochner integral,a generalization of the Lebesgue integral to functions that take values in aBanach space.

Properties

Linearity

The collection of Riemann-integrable functions on a closed interval[a,b]forms avector spaceunder the operations ofpointwise additionand multiplication by a scalar, and the operation of integration

$f\mapsto \int _{a}^{b}f(x)\;dx$

is alinear functionalon this vector space. Thus, the collection of integrable functions is closed under takinglinear combinations,and the integral of a linear combination is the linear combination of the integrals:

$\int _{a}^{b}(\alpha f+\beta g)(x)\,dx=\alpha \int _{a}^{b}f(x)\,dx+\beta \int _{a}^{b}g(x)\,dx.\,$

Similarly, the set ofreal-valued Lebesgue-integrable functions on a givenmeasure spaceEwith measureμis closed under taking linear combinations and hence form a vector space, and the Lebesgue integral

$f\mapsto \int _{E}f\,d\mu$

is a linear functional on this vector space, so that:

$\int _{E}(\alpha f+\beta g)\,d\mu =\alpha \int _{E}f\,d\mu +\beta \int _{E}g\,d\mu.$

More generally, consider the vector space of allmeasurable functionson a measure space(E,μ),taking values in alocally compactcompletetopological vector spaceVover a locally compacttopological fieldK,f:E→V.Then one may define an abstract integration map assigning to each functionfan element ofVor the symbol∞,

$f\mapsto \int _{E}f\,d\mu,\,$

that is compatible with linear combinations.In this situation, the linearity holds for the subspace of functions whose integral is an element ofV(i.e. "finite" ). The most important special cases arise whenKisR,C,or a finite extension of the fieldQ_pofp-adic numbers,andVis a finite-dimensional vector space overK,and whenK=CandVis a complexHilbert space.

Linearity, together with some natural continuity properties and normalization for a certain class of "simple" functions, may be used to give an alternative definition of the integral. This is the approach ofDaniellfor the case of real-valued functions on a setX,generalized byNicolas Bourbakito functions with values in a locally compact topological vector space. SeeHildebrandt 1953for an axiomatic characterization of the integral.

Inequalities

A number of general inequalities hold for Riemann-integrablefunctionsdefined on aclosedandboundedinterval[a,b]and can be generalized to other notions of integral (Lebesgue and Daniell).

• Upper and lower bounds.An integrable functionfon[a,b],is necessarilyboundedon that interval. Thus there arereal numbersmandMso thatm≤f (x) ≤Mfor allxin[a,b].Since the lower and upper sums offover[a,b]are therefore bounded by, respectively,m(b−a)andM(b−a),it follows that$$m(b-a)\leq \int _{a}^{b}f(x)\,dx\leq M(b-a).$$
• Inequalities between functions.Iff(x) ≤g(x)for eachxin[a,b]then each of the upper and lower sums offis bounded above by the upper and lower sums, respectively, ofg.Thus$$\int _{a}^{b}f(x)\,dx\leq \int _{a}^{b}g(x)\,dx.$$This is a generalization of the above inequalities, asM(b−a)is the integral of the constant function with valueMover[a,b].In addition, if the inequality between functions is strict, then the inequality between integrals is also strict. That is, iff(x) <g(x)for eachxin[a,b],then$$\int _{a}^{b}f(x)\,dx<\int _{a}^{b}g(x)\,dx.$$
• Subintervals.If[c,d]is a subinterval of[a,b]andf (x)is non-negative for allx,then$$\int _{c}^{d}f(x)\,dx\leq \int _{a}^{b}f(x)\,dx.$$
• Products and absolute values of functions.Iffandgare two functions, then we may consider theirpointwise productsand powers, andabsolute values:$$(fg)(x)=f(x)g(x),\;f^{2}(x)=(f(x))^{2},\;|f|(x)=|f(x)|.$$Iffis Riemann-integrable on[a,b]then the same is true for|f|,and$$\left|\int _{a}^{b}f(x)\,dx\right|\leq \int _{a}^{b}|f(x)|\,dx.$$Moreover, iffandgare both Riemann-integrable thenfgis also Riemann-integrable, and$$\left(\int _{a}^{b}(fg)(x)\,dx\right)^{2}\leq \left(\int _{a}^{b}f(x)^{2}\,dx\right)\left(\int _{a}^{b}g(x)^{2}\,dx\right).$$This inequality, known as theCauchy–Schwarz inequality,plays a prominent role inHilbert spacetheory, where the left hand side is interpreted as theinner productof twosquare-integrablefunctionsfandgon the interval[a,b].
• Hölder's inequality.Suppose thatpandqare two real numbers,1 ≤p,q≤ ∞with⁠1/p⁠+⁠1/q⁠= 1,andfandgare two Riemann-integrable functions. Then the functions|f|^pand|g|^qare also integrable and the followingHölder's inequalityholds:$$\left|\int f(x)g(x)\,dx\right|\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}\left(\int \left|g(x)\right|^{q}\,dx\right)^{1/q}.$$Forp=q= 2,Hölder's inequality becomes the Cauchy–Schwarz inequality.
• Minkowski inequality.Suppose thatp≥ 1is a real number andfandgare Riemann-integrable functions. Then|f|^p,|g|^pand|f+g|^pare also Riemann-integrable and the followingMinkowski inequalityholds:$$\left(\int \left|f(x)+g(x)\right|^{p}\,dx\right)^{1/p}\leq \left(\int \left|f(x)\right|^{p}\,dx\right)^{1/p}+\left(\int \left|g(x)\right|^{p}\,dx\right)^{1/p}.$$An analogue of this inequality for Lebesgue integral is used in construction ofL^pspaces.

Conventions

In this section,fis areal-valuedRiemann-integrablefunction.The integral

$\int _{a}^{b}f(x)\,dx$

over an interval[a,b]is defined ifa<b.This means that the upper and lower sums of the functionfare evaluated on a partitiona=x₀≤x₁≤... ≤x_n=bwhose valuesx_iare increasing. Geometrically, this signifies that integration takes place "left to right", evaluatingfwithin intervals[x_i ,x_i +1]where an interval with a higher index lies to the right of one with a lower index. The valuesaandb,the end-points of theinterval,are called thelimits of integrationoff.Integrals can also be defined ifa>b:

$\int _{a}^{b}f(x)\,dx=-\int _{b}^{a}f(x)\,dx.$

Witha=b,this implies:

$\int _{a}^{a}f(x)\,dx=0.$

The first convention is necessary in consideration of taking integrals over subintervals of[a,b];the second says that an integral taken over a degenerate interval, or apoint,should bezero.One reason for the first convention is that the integrability offon an interval[a,b]implies thatfis integrable on any subinterval[c,d],but in particular integrals have the property that ifcis anyelementof[a,b],then:

$\int _{a}^{b}f(x)\,dx=\int _{a}^{c}f(x)\,dx+\int _{c}^{b}f(x)\,dx.$

With the first convention, the resulting relation

${\begin{aligned}\int _{a}^{c}f(x)\,dx&{}=\int _{a}^{b}f(x)\,dx-\int _{c}^{b}f(x)\,dx\\&{}=\int _{a}^{b}f(x)\,dx+\int _{b}^{c}f(x)\,dx\end{aligned}}$

is then well-defined for any cyclic permutation ofa,b,andc.

Fundamental theorem of calculus

Main article:Fundamental theorem of calculus

Thefundamental theorem of calculusis the statement thatdifferentiationand integration are inverse operations: if acontinuous functionis first integrated and then differentiated, the original function is retrieved.An important consequence, sometimes called thesecond fundamental theorem of calculus,allows one to compute integrals by using an antiderivative of the function to be integrated.

First theorem

Letfbe a continuous real-valued function defined on aclosed interval[a,b].LetFbe the function defined, for allxin[a,b],by

$F(x)=\int _{a}^{x}f(t)\,dt.$

Then,Fis continuous on[a,b],differentiable on the open interval(a,b),and

$F'(x)=f(x)$

for allxin(a,b).

Second theorem

Letfbe a real-valued function defined on aclosed interval[a,b] that admits anantiderivativeFon[a,b].That is,fandFare functions such that for allxin[a,b],

$f(x)=F'(x).$

Iffis integrable on[a,b]then

$\int _{a}^{b}f(x)\,dx=F(b)-F(a).$

Extensions

Improper integrals

Main article:Improper integral

Theimproper integral$\int _{0}^{\infty }{\frac {dx}{(x+1){\sqrt {x}}}}=\pi$has unbounded intervals for both domain and range.

A "proper" Riemann integral assumes the integrand is defined and finite on a closed and bounded interval, bracketed by the limits of integration. An improper integral occurs when one or more of these conditions is not satisfied. In some cases such integrals may be defined by considering thelimitof asequenceof properRiemann integralson progressively larger intervals.

If the interval is unbounded, for instance at its upper end, then the improper integral is the limit as that endpoint goes to infinity:

$\int _{a}^{\infty }f(x)\,dx=\lim _{b\to \infty }\int _{a}^{b}f(x)\,dx.$

If the integrand is only defined or finite on a half-open interval, for instance(a,b],then again a limit may provide a finite result:

$\int _{a}^{b}f(x)\,dx=\lim _{\varepsilon \to 0}\int _{a+\epsilon }^{b}f(x)\,dx.$

That is, the improper integral is thelimitof proper integrals as one endpoint of the interval of integration approaches either a specifiedreal number,or∞,or−∞.In more complicated cases, limits are required at both endpoints, or at interior points.

Multiple integration

Main article:Multiple integral

Double integral computes volume under a surface$z=f(x,y)$

Just as the definite integral of a positive function of one variable represents theareaof the region between the graph of the function and thex-axis, thedouble integralof a positive function of two variables represents thevolumeof the region between the surface defined by the function and the plane that contains its domain.For example, a function in two dimensions depends on two real variables,xandy,and the integral of a functionfover the rectangleRgiven as theCartesian productof two intervals$R=[a,b]\times [c,d]$can be written

$\int _{R}f(x,y)\,dA$

where the differentialdAindicates that integration is taken with respect to area. Thisdouble integralcan be defined usingRiemann sums,and represents the (signed) volume under the graph ofz=f(x,y)over the domainR.Under suitable conditions (e.g., iffis continuous),Fubini's theoremstates that this integral can be expressed as an equivalent iterated integral

$\int _{a}^{b}\left[\int _{c}^{d}f(x,y)\,dy\right]\,dx.$

This reduces the problem of computing a double integral to computing one-dimensional integrals. Because of this, another notation for the integral overRuses a double integral sign:

$\iint _{R}f(x,y)\,dA.$

Integration over more general domains is possible. The integral of a functionf,with respect to volume, over ann-dimensional regionDof$\mathbb {R} ^{n}$is denoted by symbols such as:

$\int _{D}f(\mathbf {x} )d^{n}\mathbf {x} \ =\int _{D}f\,dV.$

Line integrals and surface integrals

Main articles:Line integralandSurface integral

A line integral sums together elements along a curve.

The concept of an integral can be extended to more general domains of integration, such as curved lines and surfaces inside higher-dimensional spaces. Such integrals are known as line integrals and surface integrals respectively. These have important applications in physics, as when dealing withvector fields.

Aline integral(sometimes called apath integral) is an integral where thefunctionto be integrated is evaluated along acurve.Various different line integrals are in use. In the case of a closed curve it is also called acontour integral.

The function to be integrated may be ascalar fieldor avector field.The value of the line integral is the sum of values of the field at all points on the curve, weighted by some scalar function on the curve (commonlyarc lengthor, for a vector field, thescalar productof the vector field with adifferentialvector in the curve).This weighting distinguishes the line integral from simpler integrals defined onintervals.Many simple formulas in physics have natural continuous analogs in terms of line integrals; for example, the fact thatworkis equal toforce,F,multiplied by displacement,s,may be expressed (in terms of vector quantities) as:

$W=\mathbf {F} \cdot \mathbf {s}.$

For an object moving along a pathCin avector fieldFsuch as anelectric fieldorgravitational field,the total work done by the field on the object is obtained by summing up the differential work done in moving fromstos+ds.This gives the line integral

$W=\int _{C}\mathbf {F} \cdot d\mathbf {s}.$

The definition of surface integral relies on splitting the surface into small surface elements.

Asurface integralgeneralizes double integrals to integration over asurface(which may be a curved set inspace); it can be thought of as thedouble integralanalog of theline integral.The function to be integrated may be ascalar fieldor avector field.The value of the surface integral is the sum of the field at all points on the surface. This can be achieved by splitting the surface into surface elements, which provide the partitioning for Riemann sums.

For an example of applications of surface integrals, consider a vector fieldvon a surfaceS;that is, for each pointxinS,v(x)is a vector. Imagine that a fluid flows throughS,such thatv(x)determines the velocity of the fluid atx.Thefluxis defined as the quantity of fluid flowing throughSin unit amount of time. To find the flux, one need to take thedot productofvwith the unitsurface normaltoSat each point, which will give a scalar field, which is integrated over the surface:

$\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }.$

The fluid flux in this example may be from a physical fluid such as water or air, or from electrical or magnetic flux. Thus surface integrals have applications in physics, particularly with theclassical theoryofelectromagnetism.

Contour integrals

Main article:Contour integration

Incomplex analysis,the integrand is acomplex-valued functionof a complex variablezinstead of a real function of a real variablex.When a complex function is integrated along a curve$\gamma$in the complex plane, the integral is denoted as follows

$\int _{\gamma }f(z)\,dz.$

This is known as acontour integral.

Integrals of differential forms

Main article:Differential form

See also:Volume formandDensity on a manifold

Adifferential formis a mathematical concept in the fields ofmultivariable calculus,differential topology,andtensors.Differential forms are organized by degree. For example, a one-form is a weighted sum of the differentials of the coordinates, such as:

$E(x,y,z)\,dx+F(x,y,z)\,dy+G(x,y,z)\,dz$

whereE,F,Gare functions in three dimensions. A differential one-form can be integrated over an oriented path, and the resulting integral is just another way of writing a line integral. Here the basic differentialsdx,dy,dzmeasure infinitesimal oriented lengths parallel to the three coordinate axes.

A differential two-form is a sum of the form

$G(x,y,z)\,dx\wedge dy+E(x,y,z)\,dy\wedge dz+F(x,y,z)\,dz\wedge dx.$

Here the basic two-forms$dx\wedge dy,dz\wedge dx,dy\wedge dz$measure oriented areas parallel to the coordinate two-planes. The symbol$\wedge$denotes thewedge product,which is similar to thecross productin the sense that the wedge product of two forms representing oriented lengths represents an oriented area. A two-form can be integrated over an oriented surface, and the resulting integral is equivalent to the surface integral giving the flux of$E\mathbf {i} +F\mathbf {j} +G\mathbf {k}$.

Unlike the cross product, and the three-dimensional vector calculus, the wedge product and the calculus of differential forms makes sense in arbitrary dimension and on more general manifolds (curves, surfaces, and their higher-dimensional analogs). Theexterior derivativeplays the role of thegradientandcurlof vector calculus, andStokes' theoremsimultaneously generalizes the three theorems of vector calculus: thedivergence theorem,Green's theorem,and theKelvin-Stokes theorem.

Summations

Main article:Summation § Approximation by definite integrals

The discrete equivalent of integration issummation.Summations and integrals can be put on the same foundations using the theory ofLebesgue integralsortime-scale calculus.

Functional integrals

Main article:Functional integration

An integration that is performed not over a variable (or, in physics, over a space or time dimension), but over aspace of functions,is referred to as afunctional integral.

Applications

Integrals are used extensively in many areas. For example, inprobability theory,integrals are used to determine the probability of somerandom variablefalling within a certain range.Moreover, the integral under an entireprobability density functionmust equal 1, which provides a test of whether afunctionwith no negative values could be a density function or not.

Integrals can be used for computing theareaof a two-dimensional region that has a curved boundary, as well ascomputing the volumeof a three-dimensional object that has a curved boundary. The area of a two-dimensional region can be calculated using the aforementioned definite integral.The volume of a three-dimensional object such as a disc or washer can be computed bydisc integrationusing the equation for the volume of a cylinder,$\pi r^{2}h$,where$r$is the radius. In the case of a simple disc created by rotating a curve about thex-axis, the radius is given byf(x),and its height is the differentialdx.Using an integral with boundsaandb,the volume of the disc is equal to:$$\pi \int _{a}^{b}f^{2}(x)\,dx.$$Integrals are also used in physics, in areas likekinematicsto find quantities likedisplacement,time,andvelocity.For example, inrectilinear motion,the displacement of an object over the time interval$[a,b]$is given by

$x(b)-x(a)=\int _{a}^{b}v(t)\,dt,$

where$v(t)$is the velocity expressed as a function of time.The work done by a force$F(x)$(given as a function of position) from an initial position$A$to a final position$B$is:

$W_{A\rightarrow B}=\int _{A}^{B}F(x)\,dx.$

Integrals are also used inthermodynamics,wherethermodynamic integrationis used to calculate the difference in free energy between two given states.

Computation

Analytical

The most basic technique for computing definite integrals of one real variable is based on thefundamental theorem of calculus.Letf(x)be the function ofxto be integrated over a given interval[a,b].Then, find an antiderivative off;that is, a functionFsuch thatF′ =fon the interval. Provided the integrand and integral have nosingularitieson the path of integration, by the fundamental theorem of calculus,

$\int _{a}^{b}f(x)\,dx=F(b)-F(a).$

Sometimes it is necessary to use one of the many techniques that have been developed to evaluate integrals. Most of these techniques rewrite one integral as a different one which is hopefully more tractable. Techniques includeintegration by substitution,integration by parts,integration by trigonometric substitution,andintegration by partial fractions.

Alternative methods exist to compute more complex integrals. Manynonelementary integralscan be expanded in aTaylor seriesand integrated term by term. Occasionally, the resulting infinite series can be summed analytically. The method of convolution usingMeijer G-functionscan also be used, assuming that the integrand can be written as a product of Meijer G-functions. There are also many less common ways of calculating definite integrals; for instance,Parseval's identitycan be used to transform an integral over a rectangular region into an infinite sum. Occasionally, an integral can be evaluated by a trick; for an example of this, seeGaussian integral.

Computations of volumes ofsolids of revolutioncan usually be done withdisk integrationorshell integration.

Specific results which have been worked out by various techniques are collected in thelist of integrals.

Symbolic

Main article:Symbolic integration

Many problems in mathematics, physics, and engineering involve integration where an explicit formula for the integral is desired. Extensivetables of integralshave been compiled and published over the years for this purpose. With the spread of computers, many professionals, educators, and students have turned tocomputer algebra systemsthat are specifically designed to perform difficult or tedious tasks, including integration. Symbolic integration has been one of the motivations for the development of the first such systems, likeMacsymaandMaple.

A major mathematical difficulty in symbolic integration is that in many cases, a relatively simple function does not have integrals that can be expressed inclosed forminvolving onlyelementary functions,includerationalandexponentialfunctions,logarithm,trigonometric functionsandinverse trigonometric functions,and the operations of multiplication and composition. TheRisch algorithmprovides a general criterion to determine whether the antiderivative of an elementary function is elementary and to compute the integral if is elementary. However, functions with closed expressions of antiderivatives are the exception, and consequently, computerized algebra systems have no hope of being able to find an antiderivative for a randomly constructed elementary function. On the positive side, if the 'building blocks' for antiderivatives are fixed in advance, it may still be possible to decide whether the antiderivative of a given function can be expressed using these blocks and operations of multiplication and composition and to find the symbolic answer whenever it exists. The Risch algorithm, implemented inMathematica,Mapleand othercomputer algebra systems,does just that for functions and antiderivatives built from rational functions,radicals,logarithm, and exponential functions.

Some special integrands occur often enough to warrant special study. In particular, it may be useful to have, in the set of antiderivatives, thespecial functions(like theLegendre functions,thehypergeometric function,thegamma function,theincomplete gamma functionand so on). Extending Risch's algorithm to include such functions is possible but challenging and has been an active research subject.

More recently a new approach has emerged, usingD-finite functions,which are the solutions oflinear differential equationswith polynomial coefficients. Most of the elementary and special functions areD-finite, and the integral of aD-finite function is also aD-finite function. This provides an algorithm to express the antiderivative of aD-finite function as the solution of a differential equation. This theory also allows one to compute the definite integral of aD-function as the sum of a series given by the first coefficients and provides an algorithm to compute any coefficient.

Rule-based integration systems facilitate integration. Rubi, a computer algebra system rule-based integrator, pattern matches an extensive system of symbolic integration rules to integrate a wide variety of integrands. This system uses over 6600 integration rules to compute integrals.Themethod of bracketsis a generalization of Ramanujan's master theorem that can be applied to a wide range of univariate and multivariate integrals. A set of rules are applied to the coefficients and exponential terms of the integrand's power series expansion to determine the integral. The method is closely related to theMellin transform.

Numerical

Main article:Numerical integration

Numerical quadrature methods: rectangle method, trapezoidal rule, Romberg's method, Gaussian quadrature

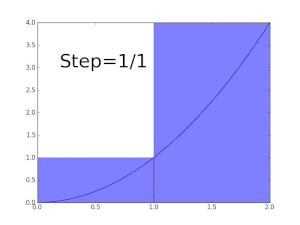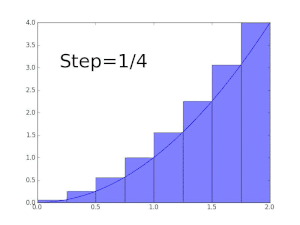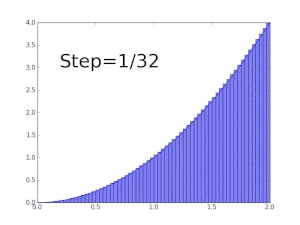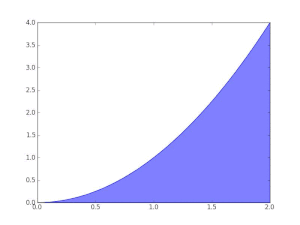
Definite integrals may be approximated using several methods ofnumerical integration.Therectangle methodrelies on dividing the region under the function into a series of rectangles corresponding to function values and multiplies by the step width to find the sum. A better approach, thetrapezoidal rule,replaces the rectangles used in a Riemann sum with trapezoids. The trapezoidal rule weights the first and last values by one half, then multiplies by the step width to obtain a better approximation.The idea behind the trapezoidal rule, that more accurate approximations to the function yield better approximations to the integral, can be carried further:Simpson's ruleapproximates the integrand by a piecewise quadratic function.

Riemann sums, the trapezoidal rule, and Simpson's rule are examples of a family of quadrature rules called theNewton–Cotes formulas.The degreenNewton–Cotes quadrature rule approximates the polynomial on each subinterval by a degreenpolynomial. This polynomial is chosen to interpolate the values of the function on the interval.Higher degree Newton–Cotes approximations can be more accurate, but they require more function evaluations, and they can suffer from numerical inaccuracy due toRunge's phenomenon.One solution to this problem isClenshaw–Curtis quadrature,in which the integrand is approximated by expanding it in terms ofChebyshev polynomials.

Romberg's methodhalves the step widths incrementally, giving trapezoid approximations denoted byT(h₀),T(h₁),and so on, whereh_k+1is half ofh_k.For each new step size, only half the new function values need to be computed; the others carry over from the previous size. It theninterpolatea polynomial through the approximations, and extrapolate toT(0).Gaussian quadratureevaluates the function at the roots of a set oforthogonal polynomials.Ann-point Gaussian method is exact for polynomials of degree up to2n− 1.

The computation of higher-dimensional integrals (for example, volume calculations) makes important use of such alternatives asMonte Carlo integration.

Mechanical

The area of an arbitrary two-dimensional shape can be determined using a measuring instrument calledplanimeter.The volume of irregular objects can be measured with precision by the fluiddisplacedas the object is submerged.

Geometrical

Main article:Quadrature (mathematics)

Area can sometimes be found viageometricalcompass-and-straightedge constructionsof an equivalentsquare.

Integration by differentiation

Kempf, Jackson and Morales demonstrated mathematical relations that allow an integral to be calculated by means ofdifferentiation.Their calculus involves theDirac delta functionand thepartial derivativeoperator$\partial _{x}$.This can also be applied tofunctional integrals,allowing them to be computed byfunctional differentiation.

Examples

Using the fundamental theorem of calculus

Thefundamental theorem of calculusallows straightforward calculations of basic functions:

$\int _{0}^{\pi }\sin(x)\,dx=-\cos(x){\big |}_{x=0}^{x=\pi }=-\cos(\pi )-{\big (}-\cos(0){\big )}=2.$

See also

• Integral equation– Equations with an unknown function under an integral sign
• Integral symbol– Mathematical symbol used to denote integrals and antiderivatives
• Lists of integrals

Bibliography

• Anton, Howard; Bivens, Irl C.; Davis, Stephen (2016),Calculus: Early Transcendentals(11th ed.), John Wiley & Sons,ISBN978-1-118-88382-2
• Apostol, Tom M.(1967),Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra(2nd ed.), Wiley,ISBN978-0-471-00005-1
• Bourbaki, Nicolas(2004),Integration I,Springer-Verlag,ISBN3-540-41129-1.In particular chapters III and IV.
• Burton, David M. (2011),The History of Mathematics: An Introduction(7th ed.), McGraw-Hill,ISBN978-0-07-338315-6
• Cajori, Florian(1929),A History Of Mathematical Notations Volume II,Open Court Publishing,ISBN978-0-486-67766-8
• Dahlquist, Germund;Björck, Åke (2008),"Chapter 5: Numerical Integration",Numerical Methods in Scientific Computing, Volume I,Philadelphia:SIAM,archived fromthe originalon 2007-06-15
• Feller, William(1966),An introduction to probability theory and its applications,John Wiley & Sons
• Folland, Gerald B.(1999),Real Analysis: Modern Techniques and Their Applications(2nd ed.), John Wiley & Sons,ISBN0-471-31716-0
• Fourier, Jean Baptiste Joseph(1822),Théorie analytique de la chaleur,Chez Firmin Didot, père et fils, p. §231
  Available in translation asFourier, Joseph (1878),The analytical theory of heat,Freeman, Alexander (trans.), Cambridge University Press, pp.200–201
• Gonzalez, Ivan; Jiu, Lin; Moll, Victor H. (1 January 2020), "An extension of the method of brackets. Part 2",Open Mathematics,18(1):983–995,arXiv:1707.08942,doi:10.1515/math-2020-0062,ISSN2391-5455,S2CID222004668
• Heath, T. L.,ed. (2002),The Works of Archimedes,Dover,ISBN978-0-486-42084-4
  (Originally published by Cambridge University Press, 1897, based on J. L. Heiberg's Greek version.)
• Hildebrandt, T. H.(1953),"Integration in abstract spaces",Bulletin of the American Mathematical Society,59(2):111–139,doi:10.1090/S0002-9904-1953-09694-X,ISSN0273-0979
• Kahaner, David;Moler, Cleve;Nash, Stephen (1989), "Chapter 5: Numerical Quadrature",Numerical Methods and Software,Prentice Hall,ISBN978-0-13-627258-8
• Kallio, Bruce Victor (1966),A History of the Definite Integral(PDF)(M.A. thesis), University of British Columbia, archived fromthe originalon 2014-03-05,retrieved2014-02-28
• Katz, Victor J.(2009),A History of Mathematics: An Introduction,Addison-Wesley,ISBN978-0-321-38700-4
• Kempf, Achim; Jackson, David M.; Morales, Alejandro H. (2015), "How to (path-)integrate by differentiating",Journal of Physics: Conference Series,626(1),IOP Publishing:012015,arXiv:1507.04348,Bibcode:2015JPhCS.626a2015K,doi:10.1088/1742-6596/626/1/012015,S2CID119642596
• Krantz, Steven G.(1991),Real Analysis and Foundations,CRC Press,ISBN0-8493-7156-2
• Leibniz, Gottfried Wilhelm(1899), Gerhardt, Karl Immanuel (ed.),Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band,Berlin: Mayer & Müller
• Lieb, Elliott;Loss, Michael(2001),Analysis,Graduate Studies in Mathematics,vol. 14 (2nd ed.),American Mathematical Society,ISBN978-0821827833
• Montesinos, Vicente; Zizler, Peter; Zizler, Václav (2015),An Introduction to Modern Analysis(illustrated ed.), Springer,ISBN978-3-319-12481-0
• Paul J. Nahin (2015),Inside Interesting Integrals,Springer, ISBN 978-1-4939-1276-6.
• Rich, Albert; Scheibe, Patrick; Abbasi, Nasser (16 December 2018), "Rule-based integration: An extensive system of symbolic integration rules",Journal of Open Source Software,3(32): 1073,Bibcode:2018JOSS....3.1073R,doi:10.21105/joss.01073,S2CID56487062
• Rudin, Walter(1987), "Chapter 1: Abstract Integration",Real and Complex Analysis(International ed.), McGraw-Hill,ISBN978-0-07-100276-9
• Saks, Stanisław(1964),Theory of the integral(English translation by L. C. Young. With two additional notes by Stefan Banach. Second revised ed.), New York: Dover
• Siegmund-Schultze, Reinhard(2008), "Henri Lebesgue", in Timothy Gowers; June Barrow-Green; Imre Leader (eds.),Princeton Companion to Mathematics,Princeton University Press,ISBN978-0-691-11880-2.
• Stillwell, John(1989),Mathematics and Its History,Springer,ISBN0-387-96981-0
• Stoer, Josef;Bulirsch, Roland(2002), "Topics in Integration",Introduction to Numerical Analysis(3rd ed.), Springer,ISBN978-0-387-95452-3.
• Struik, Dirk Jan,ed. (1986),A Source Book in Mathematics, 1200-1800,Princeton, New Jersey: Princeton University Press,ISBN0-691-08404-1
• Cornel Ioan Vălean (2019),(Almost Impossible) Integrals, Sums, and Series,Springer, ISBN 978-3-030-02461-1.
• Cornel Ioan Vălean (2023),More (Almost Impossible) Integrals, Sums, and Series,Springer, ISBN 978-3-031-21261-1.
• "Arabic mathematical notation",W3C,2006

External links

• "Integral",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• Online Integral Calculator,Wolfram Alpha.

Online books

• Keisler, H. Jerome,Elementary Calculus: An Approach Using Infinitesimals,University of Wisconsin
• Stroyan, K. D.,A Brief Introduction to Infinitesimal Calculus,University of Iowa
• Mauch, Sean,Sean's Applied Math Book,CIT, an online textbook that includes a complete introduction to calculus
• Crowell, Benjamin,Calculus,Fullerton College, an online textbook
• Garrett, Paul,Notes on First-Year Calculus
• Hussain, Faraz,Understanding Calculus,an online textbook
• Johnson, William Woolsey (1909)Elementary Treatise on Integral Calculus,link fromHathiTrust.
• Kowalk, W. P.,Integration Theory,University of Oldenburg. A new concept to an old problem. Online textbook
• Sloughter, Dan,Difference Equations to Differential Equations,an introduction to calculus
• Numerical Methods of IntegrationatHolistic Numerical Methods Institute
• P. S. Wang,Evaluation of Definite Integrals by Symbolic Manipulation(1972) — a cookbook of definite integral techniques