Isotoxal figure
Ingeometry,apolytope(for example, apolygonor apolyhedron) or atilingisisotoxal(fromGreekτόξον'arc') oredge-transitiveif itssymmetriesacttransitivelyon itsedges.Informally, this means that there is only one type of edge to the object: given two edges, there is atranslation,rotation,and/orreflectionthat will move one edge to the other while leaving the region occupied by the object unchanged.
Isotoxal polygons[edit]
An isotoxal polygon is an even-sided i.e.equilateral polygon,but not all equilateral polygons are isotoxal. Thedualsof isotoxal polygons areisogonal polygons.Isotoxal-gons arecentrally symmetric,thus are alsozonogons.
In general, a (non-regular) isotoxal-gon hasdihedral symmetry.For example, a (non-square)rhombusis an isotoxal "×-gon "(quadrilateral) withsymmetry. Allregular-gons(also with odd) are isotoxal, having double the minimum symmetry order: a regular-gon hasdihedral symmetry.
An isotoxal-gon with outer internal anglecan be denoted byThe inner internal anglemay be less or greater thanmaking convex or concave polygons respectively.
Astar-goncan also be isotoxal, denoted bywithand with thegreatest common divisorwhereis theturning numberordensity.[1]Concave inner vertices can be defined forIfthenis "reduced" to a compoundofrotated copies of
Caution:
- The vertices ofare not always placed like those ofwhereas the vertices of the regularare placed like those of the regular
A set of"uniform" tilings,actuallyisogonal tilingsusing isotoxal polygons as less symmetric faces than regular ones, can be defined.
| Number of sides: | 2×2 (Cent. sym.) |
2×3 | 2×4 (Cent. sym.) |
2×5 | 2×6 (Cent. sym.) |
2×7 | 2×8 (Cent. sym.) |
|---|---|---|---|---|---|---|---|
Convex: Concave: |
  |
  |
  |
  |
  |
  | |
| 2-turn |
-- |  |
 |
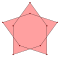  |
  |
  |
  |
| 3-turn |
-- | -- |  |
 |
 |
  |
  |
| 4-turn |
-- | -- | -- |  |
 |
 |
 |
| 5-turn |
-- | -- | -- | -- |  |
 |
 |
| 6-turn |
-- | -- | -- | -- | -- |  |
 |
| 7-turn |
-- | -- | -- | -- | -- | -- |  |
Isotoxal polyhedra and tilings[edit]
Regular polyhedraare isohedral (face-transitive), isogonal (vertex-transitive), and isotoxal (edge-transitive).
Quasiregularpolyhedra, like thecuboctahedronand theicosidodecahedron,are isogonal and isotoxal, but not isohedral. Their duals, including therhombic dodecahedronand therhombic triacontahedron,are isohedral and isotoxal, but not isogonal.
| Quasiregular polyhedron |
Quasiregular dual polyhedron |
Quasiregular star polyhedron |
Quasiregular dual star polyhedron |
Quasiregular tiling |
Quasiregular dual tiling |
|---|---|---|---|---|---|
 Acuboctahedronis an isogonal and isotoxal polyhedron |
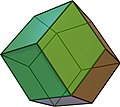 Arhombic dodecahedronis an isohedral and isotoxal polyhedron |
 Agreat icosidodecahedronis an isogonal and isotoxal star polyhedron |
 Agreat rhombic triacontahedronis an isohedral and isotoxal star polyhedron |
 Thetrihexagonal tilingis an isogonal and isotoxal tiling |
 Therhombille tilingis an isohedral and isotoxal tiling with p6m (*632) symmetry. |
Not everypolyhedronor 2-dimensionaltessellationconstructed fromregular polygonsis isotoxal. For instance, thetruncated icosahedron(the familiar soccerball) is not isotoxal, as it has two edge types: hexagon-hexagon and hexagon-pentagon, and it is not possible for a symmetry of the solid to move a hexagon-hexagon edge onto a hexagon-pentagon edge.
An isotoxal polyhedron has the samedihedral anglefor all edges.
The dual of a convex polyhedron is also a convex polyhedron.[2]
The dual of a non-convex polyhedron is also a non-convex polyhedron.[2](By contraposition.)
The dual of an isotoxal polyhedron is also an isotoxal polyhedron. (See theDual polyhedronarticle.)
There are nineconvexisotoxal polyhedra: the five (regular)Platonic solids,the two (quasiregular) common cores of dual Platonic solids, and their two duals.
There are fourteen non-convex isotoxal polyhedra: the four (regular)Kepler–Poinsot polyhedra,the two (quasiregular) common cores of dual Kepler–Poinsot polyhedra, and their two duals, plus the three quasiregular ditrigonal (3 |p q) star polyhedra, and their three duals.
There are at least five isotoxal polyhedral compounds: the fiveregular polyhedral compounds;their five duals are also the five regular polyhedral compounds (or one chiral twin).
There are at least five isotoxal polygonal tilings of the Euclidean plane, and infinitely many isotoxal polygonal tilings of the hyperbolic plane, including the Wythoff constructions from theregular hyperbolic tilings{p,q}, and non-right (p q r) groups.
See also[edit]
References[edit]
- ^Tilings and patterns,Branko Gruenbaum, G. C. Shephard, 1987, 2.5 Tilings using star polygons, pp. 82–85.
- ^ab"duality".maths.ac-noumea.nc.Retrieved2020-09-30.
- Peter R. Cromwell,Polyhedra,Cambridge University Press, 1997,ISBN0-521-55432-2,Transitivity, p. 371
- Grünbaum, Branko;Shephard, G. C. (1987).Tilings and Patterns.New York: W. H. Freeman.ISBN0-7167-1193-1.(6.4 Isotoxal tilings, pp. 309–321)
- Coxeter, Harold Scott MacDonald;Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra",Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences,246(916): 401–450,Bibcode:1954RSPTA.246..401C,doi:10.1098/rsta.1954.0003,ISSN0080-4614,JSTOR91532,MR0062446,S2CID202575183

































































