Kurtosis

Inprobability theoryandstatistics,kurtosis(fromGreek:κυρτός,kyrtosorkurtos,meaning "curved, arching" ) is a measure of the "tailedness" of theprobability distributionof areal-valuedrandom variable.Likeskewness,kurtosis describes a particular aspect of a probability distribution. There are different ways to quantify kurtosis for a theoretical distribution, and there are corresponding ways of estimating it using a sample from a population. Different measures of kurtosis may have differentinterpretations.

The standard measure of a distribution's kurtosis, originating withKarl Pearson,is a scaled version of the fourthmomentof the distribution. This number is related to the tails of the distribution, not its peak;hence, the sometimes-seen characterization of kurtosis as "peakedness"is incorrect. For this measure, higher kurtosis corresponds to greater extremity ofdeviations(oroutliers), and not the configuration of data nearthe mean.

It is common to compare the excess kurtosis (defined below) of a distribution to 0. This value 0 is the excess kurtosis of any univariatenormal distribution.Distributions with negative excess kurtosis are said to beplatykurtic,although this does not imply the distribution is "flat-topped" as is sometimes stated. Rather, it means the distribution produces fewer and/or less extreme outliers than the normal distribution. An example of a platykurtic distribution is theuniform distribution,which does not produce outliers. Distributions with a positive excess kurtosis are said to beleptokurtic.An example of a leptokurtic distribution is theLaplace distribution,which has tails that asymptotically approach zero more slowly than a Gaussian, and therefore produces more outliers than the normal distribution. It is common practice to use excess kurtosis, which is defined as Pearson's kurtosis minus 3, to provide a simple comparison to thenormal distribution.Some authors and software packages use "kurtosis" by itself to refer to the excess kurtosis. For clarity and generality, however, this article explicitly indicates where non-excess kurtosis is meant.

Alternative measures of kurtosis are: theL-kurtosis,which is a scaled version of the fourthL-moment;measures based on four population or samplequantiles.These are analogous to the alternative measures ofskewnessthat are not based on ordinary moments.

Pearson moments

The kurtosis is the fourthstandardized moment,defined as $$\operatorname {Kurt} [X]=\operatorname {E} \left[\left({\frac {X-\mu }{\sigma }}\right)^{4}\right]={\frac {\operatorname {E} \left[(X-\mu )^{4}\right]}{\left(\operatorname {E} \left[(X-\mu )^{2}\right]\right)^{2}}}={\frac {\mu _{4}}{\sigma ^{4}}},$$ whereμ₄is the fourthcentral momentandσis thestandard deviation.Several letters are used in the literature to denote the kurtosis. A very common choice isκ,which is fine as long as it is clear that it does not refer to acumulant.Other choices includeγ₂,to be similar to the notation for skewness, although sometimes this is instead reserved for the excess kurtosis.

The kurtosis is bounded below by the squaredskewnessplus 1: $${\frac {\mu _{4}}{\sigma ^{4}}}\geq \left({\frac {\mu _{3}}{\sigma ^{3}}}\right)^{2}+1,$$ whereμ₃is the thirdcentral moment.The lower bound is realized by theBernoulli distribution.There is no upper limit to the kurtosis of a general probability distribution, and it may be infinite.

A reason why some authors favor the excess kurtosis is that cumulants areextensive.Formulas related to the extensive property are more naturally expressed in terms of the excess kurtosis. For example, letX₁,...,X_nbe independent random variables for which the fourth moment exists, and letYbe the random variable defined by the sum of theX_i.The excess kurtosis ofYis $$\operatorname {Kurt} [Y]-3={\frac {1}{\left(\sum _{j=1}^{n}\sigma _{j}^{\,2}\right)^{2}}}\sum _{i=1}^{n}\sigma _{i}^{\,4}\cdot \left(\operatorname {Kurt} \left[X_{i}\right]-3\right),$$ where$\sigma _{i}$is the standard deviation of$X_{i}$.In particular if all of theX_ihave the same variance, then this simplifies to $$\operatorname {Kurt} [Y]-3={1 \over n^{2}}\sum _{i=1}^{n}\left(\operatorname {Kurt} \left[X_{i}\right]-3\right).$$

The reason not to subtract 3 is that the baremomentbetter generalizes tomultivariate distributions,especially when independence is not assumed. Thecokurtosisbetween pairs of variables is an order fourtensor.For a bivariate normal distribution, the cokurtosis tensor has off-diagonal terms that are neither 0 nor 3 in general, so attempting to "correct" for an excess becomes confusing. It is true, however, that the joint cumulants of degree greater than two for anymultivariate normal distributionare zero.

For two random variables,XandY,not necessarily independent, the kurtosis of the sum,X+Y,is $${\begin{aligned}\operatorname {Kurt} [X+Y]={1 \over \sigma _{X+Y}^{4}}{\big (}&\sigma _{X}^{4}\operatorname {Kurt} [X]+4\sigma _{X}^{3}\sigma _{Y}\operatorname {Cokurt} [X,X,X,Y]\\&{}+6\sigma _{X}^{2}\sigma _{Y}^{2}\operatorname {Cokurt} [X,X,Y,Y]\\[6pt]&{}+4\sigma _{X}\sigma _{Y}^{3}\operatorname {Cokurt} [X,Y,Y,Y]+\sigma _{Y}^{4}\operatorname {Kurt} [Y]{\big )}.\end{aligned}}$$ Note that the fourth-powerbinomial coefficients(1, 4, 6, 4, 1) appear in the above equation.

Interpretation

The exact interpretation of the Pearson measure of kurtosis (or excess kurtosis) used to be disputed, but is now settled. As Westfall notes in 2014,"...its only unambiguous interpretation is in terms of tail extremity; i.e., either existing outliers (for the sample kurtosis) or propensity to produce outliers (for the kurtosis of a probability distribution)."The logic is simple: Kurtosis is the average (orexpected value) of the standardized data raised to the fourth power. Standardized values that are less than 1 (i.e., data within one standard deviation of the mean, where the "peak" would be) contribute virtually nothing to kurtosis, since raising a number that is less than 1 to the fourth power makes it closer to zero. The only data values (observed or observable) that contribute to kurtosis in any meaningful way are those outside the region of the peak; i.e., the outliers. Therefore, kurtosis measures outliers only; it measures nothing about the "peak".

Many incorrect interpretations of kurtosis that involve notions of peakedness have been given. One is that kurtosis measures both the "peakedness" of the distribution and theheaviness of its tail.Various other incorrect interpretations have been suggested, such as "lack of shoulders" (where the "shoulder" is defined vaguely as the area between the peak and the tail, or more specifically as the area about onestandard deviationfrom the mean) or "bimodality".Balanda andMacGillivrayassert that the standard definition of kurtosis "is a poor measure of the kurtosis, peakedness, or tail weight of a distribution"and instead propose to "define kurtosis vaguely as the location- and scale-free movement ofprobability massfrom the shoulders of a distribution into its center and tails ".

Moors' interpretation

In 1986 Moors gave an interpretation of kurtosis.Let $$Z={\frac {X-\mu }{\sigma }},$$ whereXis a random variable,μis the mean andσis the standard deviation.

Now by definition of the kurtosis$\kappa$,and by the well-known identity$E\left[V^{2}\right]=\operatorname {var} [V]+[E[V]]^{2},$ $$\kappa =E\left[Z^{4}\right]=\operatorname {var} \left[Z^{2}\right]+\left[E\left[Z^{2}\right]\right]^{2}=\operatorname {var} \left[Z^{2}\right]+[\operatorname {var} [Z]]^{2}=\operatorname {var} \left[Z^{2}\right]+1.$$

The kurtosis can now be seen as a measure of the dispersion ofZ²around its expectation. Alternatively it can be seen to be a measure of the dispersion ofZaround +1 and −1.κattains its minimal value in a symmetric two-point distribution. In terms of the original variableX,the kurtosis is a measure of the dispersion ofXaround the two valuesμ±σ.

High values ofκarise in two circumstances:

• where the probability mass is concentrated around the mean and the data-generating process produces occasional values far from the mean,
• where the probability mass is concentrated in the tails of the distribution.

Maximal entropy

The entropy of a distribution is$\int p(x)\ln p(x)\,dx$.

For any$\mu \in \mathbb {R} ^{n},\Sigma \in \mathbb {R} ^{n\times n}$with$\Sigma$positive definite, among all probability distributions on$\mathbb {R} ^{n}$with mean$\mu$and covariance$\Sigma$,the normal distribution${\mathcal {N}}(\mu,\Sigma )$has the largest entropy.

Since mean$\mu$and covariance$\Sigma$are the first two moments, it is natural to consider extension to higher moments. In fact, byLagrange multipliermethod, for any prescribed first n moments, if there exists some probability distribution of form$p(x)\propto e^{\sum _{i}a_{i}x_{i}+\sum _{ij}b_{ij}x_{i}x_{j}+\cdots +\sum _{i_{1}\cdots i_{n}}x_{i_{1}}\cdots x_{i_{n}}}$that has the prescribed moments (if it is feasible), then it is the maximal entropy distribution under the given constraints.

By serial expansion,$${\begin{aligned}&\int {\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}-{\frac {1}{4}}gx^{4}}x^{2n}\,dx\\[6pt]={}&{\frac {1}{\sqrt {2\pi }}}\int e^{-{\frac {1}{2}}x^{2}-{\frac {1}{4}}gx^{4}}x^{2n}\,dx\\[6pt]={}&\sum _{k}{\frac {1}{k!}}(-g/4)^{k}(2n+4k-1)!!\\[6pt]={}&(2n-1)!!-{\frac {1}{4}}g(2n+3)!!+O(g^{2})\end{aligned}}$$so if a random variable has probability distribution$p(x)=e^{-{\frac {1}{2}}x^{2}-{\frac {1}{4}}gx^{4}}/Z$,where$Z$is a normalization constant, then its kurtosis is$3-6g+O(g^{2})$.

Excess kurtosis

Theexcess kurtosisis defined as kurtosis minus 3. There are 3 distinct regimes as described below.

Mesokurtic

Distributions with zero excess kurtosis are calledmesokurtic,ormesokurtotic.The most prominent example of a mesokurtic distribution is the normal distribution family, regardless of the values of itsparameters.A few other well-known distributions can be mesokurtic, depending on parameter values: for example, thebinomial distributionis mesokurtic for${\textstyle p=1/2\pm {\sqrt {1/12}}}$.

Leptokurtic

A distribution withpositiveexcess kurtosis is calledleptokurtic,orleptokurtotic."Lepto-" means "slender".In terms of shape, a leptokurtic distribution hasfatter tails.Examples of leptokurtic distributions include theStudent's t-distribution,Rayleigh distribution,Laplace distribution,exponential distribution,Poisson distributionand thelogistic distribution.Such distributions are sometimes termedsuper-Gaussian.

Three symmetric increasingly leptokurtic probability density functions; their intersections are indicated by vertical lines.

Platykurtic

Thecoin tossis the most platykurtic distribution

A distribution withnegativeexcess kurtosis is calledplatykurtic,orplatykurtotic."Platy-" means "broad".In terms of shape, a platykurtic distribution hasthinner tails.Examples of platykurtic distributions include thecontinuousanddiscrete uniform distributions,and theraised cosine distribution.The most platykurtic distribution of all is theBernoulli distributionwithp= 1/2 (for example the number of times one obtains "heads" when flipping a coin once, acoin toss), for which the excess kurtosis is −2.

Graphical examples

The Pearson type VII family

pdffor the Pearson type VII distribution with excess kurtosis of infinity (red); 2 (blue); and 0 (black)

log-pdf for the Pearson type VII distribution with excess kurtosis of infinity (red); 2 (blue); 1, 1/2, 1/4, 1/8, and 1/16 (gray); and 0 (black)

The effects of kurtosis are illustrated using aparametric familyof distributions whose kurtosis can be adjusted while their lower-order moments and cumulants remain constant. Consider thePearson type VII family,which is a special case of thePearson type IV familyrestricted to symmetric densities. Theprobability density functionis given by $$f(x;a,m)={\frac {\Gamma (m)}{a\,{\sqrt {\pi }}\,\Gamma (m-1/2)}}\left[1+\left({\frac {x}{a}}\right)^{2}\right]^{-m},$$ whereais ascale parameterandmis ashape parameter.

All densities in this family are symmetric. Thekth moment exists providedm> (k+ 1)/2. For the kurtosis to exist, we requirem> 5/2. Then the mean andskewnessexist and are both identically zero. Settinga²= 2m− 3 makes the variance equal to unity. Then the only free parameter ism,which controls the fourth moment (and cumulant) and hence the kurtosis. One can reparameterize with$m=5/2+3/\gamma _{2}$,where$\gamma _{2}$is the excess kurtosis as defined above. This yields a one-parameter leptokurtic family with zero mean, unit variance, zero skewness, and arbitrary non-negative excess kurtosis. The reparameterized density is $$g(x;\gamma _{2})=f\left(x;\;a={\sqrt {2+{\frac {6}{\gamma _{2}}}}},\;m={\frac {5}{2}}+{\frac {3}{\gamma _{2}}}\right).$$

In the limit as$\gamma _{2}\to \infty$one obtains the density $$g(x)=3\left(2+x^{2}\right)^{-{\frac {5}{2}}},$$ which is shown as the red curve in the images on the right.

In the other direction as$\gamma _{2}\to 0$one obtains thestandard normaldensity as the limiting distribution, shown as the black curve.

In the images on the right, the blue curve represents the density$x\mapsto g(x;2)$with excess kurtosis of 2. The top image shows that leptokurtic densities in this family have a higher peak than the mesokurtic normal density, although this conclusion is only valid for this select family of distributions. The comparatively fatter tails of the leptokurtic densities are illustrated in the second image, which plots the natural logarithm of the Pearson type VII densities: the black curve is the logarithm of the standard normal density, which is aparabola.One can see that the normal density allocates little probability mass to the regions far from the mean ( "has thin tails" ), compared with the blue curve of the leptokurtic Pearson type VII density with excess kurtosis of 2. Between the blue curve and the black are other Pearson type VII densities withγ₂= 1, 1/2, 1/4, 1/8, and 1/16. The red curve again shows the upper limit of the Pearson type VII family, with$\gamma _{2}=\infty$(which, strictly speaking, means that the fourth moment does not exist). The red curve decreases the slowest as one moves outward from the origin ( "has fat tails" ).

Other well-known distributions

Probability density functionsfor selected distributions withmean0,variance1 and different excess kurtosis

Logarithmsofprobability density functionsfor selected distributions withmean0,variance1 and different excess kurtosis

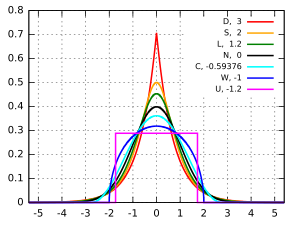
Several well-known, unimodal, and symmetric distributions from different parametric families are compared here. Each has a mean and skewness of zero. The parameters have been chosen to result in a variance equal to 1 in each case. The images on the right show curves for the following seven densities, on alinear scaleandlogarithmic scale:

• D:Laplace distribution,also known as the double exponential distribution, red curve (two straight lines in the log-scale plot), excess kurtosis = 3
• S:hyperbolic secant distribution,orange curve, excess kurtosis = 2
• L:logistic distribution,green curve, excess kurtosis = 1.2
• N:normal distribution,black curve (inverted parabola in the log-scale plot), excess kurtosis = 0
• C:raised cosine distribution,cyan curve, excess kurtosis = −0.593762...
• W:Wigner semicircle distribution,blue curve, excess kurtosis = −1
• U:uniform distribution,magenta curve (shown for clarity as a rectangle in both images), excess kurtosis = −1.2.

Note that in these cases the platykurtic densities have boundedsupport,whereas the densities with positive or zero excess kurtosis are supported on the wholereal line.

One cannot infer that high or low kurtosis distributions have the characteristics indicated by these examples. There exist platykurtic densities with infinite support,

• e.g.,exponential power distributionswith sufficiently large shape parameterb

and there exist leptokurtic densities with finite support.

• e.g., a distribution that is uniform between −3 and −0.3, between −0.3 and 0.3, and between 0.3 and 3, with the same density in the (−3, −0.3) and (0.3, 3) intervals, but with 20 times more density in the (−0.3, 0.3) interval

Also, there exist platykurtic densities with infinite peakedness,

• e.g., an equal mixture of thebeta distributionwith parameters 0.5 and 1 with its reflection about 0.0

and there exist leptokurtic densities that appear flat-topped,

• e.g., a mixture of distribution that is uniform between −1 and 1 with a T(4.0000001)Student's t-distribution,with mixing probabilities 0.999 and 0.001.

Sample kurtosis

Definitions

A natural but biased estimator

For asampleofnvalues, amethod of momentsestimator of the population excess kurtosis can be defined as $$g_{2}={\frac {m_{4}}{m_{2}^{2}}}-3={\frac {{\tfrac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{4}}{\left[{\tfrac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}\right]^{2}}}-3$$ wherem₄is the fourth samplemoment about the mean,m₂is the second sample moment about the mean (that is, thesample variance),x_iis thei^thvalue, and${\overline {x}}$is thesample mean.

This formula has the simpler representation, $$g_{2}={\frac {1}{n}}\sum _{i=1}^{n}z_{i}^{4}-3$$ where the$z_{i}$values are the standardized data values using the standard deviation defined usingnrather thann− 1 in the denominator.

For example, suppose the data values are 0, 3, 4, 1, 2, 3, 0, 2, 1, 3, 2, 0, 2, 2, 3, 2, 5, 2, 3, 999.

Then the$z_{i}$values are −0.239, −0.225, −0.221, −0.234, −0.230, −0.225, −0.239, −0.230, −0.234, −0.225, −0.230, −0.239, −0.230, −0.230, −0.225, −0.230, −0.216, −0.230, −0.225, 4.359

and the$z_{i}^{4}$values are 0.003, 0.003, 0.002, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.002, 0.003, 0.003, 360.976.

The average of these values is 18.05 and the excess kurtosis is thus 18.05 − 3 = 15.05. This example makes it clear that data near the "middle" or "peak" of the distribution do not contribute to the kurtosis statistic, hence kurtosis does not measure "peakedness". It is simply a measure of the outlier, 999 in this example.

Standard unbiased estimator

Given a sub-set of samples from a population, the sample excess kurtosis$g_{2}$above is abiased estimatorof the population excess kurtosis. An alternative estimator of the population excess kurtosis, which is unbiased in random samples of a normal distribution, is defined as follows: $${\begin{aligned}G_{2}&={\frac {k_{4}}{k_{2}^{2}}}\\[6pt]&={\frac {n^{2}\,[(n+1)\,m_{4}-3\,(n-1)\,m_{2}^{2}]}{(n-1)\,(n-2)\,(n-3)}}\;{\frac {(n-1)^{2}}{n^{2}\,m_{2}^{2}}}\\[6pt]&={\frac {n-1}{(n-2)\,(n-3)}}\left[(n+1)\,{\frac {m_{4}}{m_{2}^{2}}}-3\,(n-1)\right]\\[6pt]&={\frac {n-1}{(n-2)\,(n-3)}}\left[(n+1)\,g_{2}+6\right]\\[6pt]&={\frac {(n+1)\,n\,(n-1)}{(n-2)\,(n-3)}}\;{\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{4}}{\left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}\right)^{2}}}-3\,{\frac {(n-1)^{2}}{(n-2)\,(n-3)}}\\[6pt]&={\frac {(n+1)\,n}{(n-1)\,(n-2)\,(n-3)}}\;{\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{4}}{k_{2}^{2}}}-3\,{\frac {(n-1)^{2}}{(n-2)(n-3)}}\end{aligned}}$$ wherek₄is the unique symmetricunbiasedestimator of the fourthcumulant,k₂is the unbiased estimate of the second cumulant (identical to the unbiased estimate of the sample variance),m₄is the fourth sample moment about the mean,m₂is the second sample moment about the mean,x_iis thei^thvalue, and${\bar {x}}$is the sample mean. This adjusted Fisher–Pearson standardized moment coefficient$G_{2}$is the version found inExceland several statistical packages includingMinitab,SAS,andSPSS.

Unfortunately, in nonnormal samples$G_{2}$is itself generally biased.

Upper bound

An upper bound for the sample kurtosis ofn(n> 2) real numbers is $$g_{2}\leq {\frac {1}{2}}{\frac {n-3}{n-2}}g_{1}^{2}+{\frac {n}{2}}-3.$$ where$g_{1}=m_{3}/m_{2}^{3/2}$is the corresponding sample skewness.

Variance under normality

The variance of the sample kurtosis of a sample of sizenfrom thenormal distributionis $$\operatorname {var} (g_{2})={\frac {24n(n-1)^{2}}{(n-3)(n-2)(n+3)(n+5)}}$$

Stated differently, under the assumption that the underlying random variable$X$is normally distributed, it can be shown that${\sqrt {n}}g_{2}\,\xrightarrow {d} \,{\mathcal {N}}(0,24)$.

Applications

The sample kurtosis is a useful measure of whether there is a problem with outliers in a data set. Larger kurtosis indicates a more serious outlier problem, and may lead the researcher to choose alternative statistical methods.

D'Agostino's K-squared testis agoodness-of-fitnormality testbased on a combination of the sample skewness and sample kurtosis, as is theJarque–Bera testfor normality.

For non-normal samples, the variance of the sample variance depends on the kurtosis; for details, please seevariance.

Pearson's definition of kurtosis is used as an indicator of intermittency inturbulence.It is also used in magnetic resonance imaging to quantify non-Gaussian diffusion.

A concrete example is the following lemma by He, Zhang, and Zhang: Assume a random variable$X$has expectation$E[X]=\mu$,variance$E\left[(X-\mu )^{2}\right]=\sigma ^{2}$and kurtosis$\kappa ={\tfrac {1}{\sigma ^{4}}}E\left[(X-\mu )^{4}\right].$ Assume we sample$n={\tfrac {2{\sqrt {3}}+3}{3}}\kappa \log {\tfrac {1}{\delta }}$many independent copies. Then $$\Pr \left[\max _{i=1}^{n}X_{i}\leq \mu \right]\leq \delta \quad {\text{and}}\quad \Pr \left[\min _{i=1}^{n}X_{i}\geq \mu \right]\leq \delta.$$

This shows that with$\Theta (\kappa \log {\tfrac {1}{\delta }})$many samples, we will see one that is above the expectation with probability at least$1-\delta$. In other words: If the kurtosis is large, we might see a lot values either all below or above the mean.

Kurtosis convergence

Applyingband-pass filterstodigital images,kurtosis values tend to be uniform, independent of the range of the filter. This behavior, termedkurtosis convergence,can be used to detect image splicing inforensic analysis.

Other measures

A different measure of "kurtosis" is provided by usingL-momentsinstead of the ordinary moments.

See also

• Kurtosis risk
• Maximum entropy probability distribution

Further reading

• Kim, Tae-Hwan; White, Halbert (2003)."On More Robust Estimation of Skewness and Kurtosis: Simulation and Application to the S&P500 Index".Finance Research Letters.1:56–70.doi:10.1016/S1544-6123(03)00003-5.S2CID16913409.Alternative source(Comparison of kurtosis estimators)
• Seier, E.; Bonett, D.G. (2003). "Two families of kurtosis measures".Metrika.58:59–70.doi:10.1007/s001840200223.S2CID115990880.

External links

• "Excess coefficient",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• Kurtosis calculator
• Free Online Software (Calculator)computes various types of skewness and kurtosis statistics for any dataset (includes small and large sample tests)..
• Kurtosison theEarliest known uses of some of the words of mathematics
• Celebrating 100 years of Kurtosisa history of the topic, with different measures of kurtosis.