Legendre transformation

This article is about an involution transform commonly used in classical mechanics and thermodynamics. For the integral transform using Legendre polynomials as kernels, seeLegendre transform (integral transform).

The function$f(x)$is defined on the interval${\textstyle [a,b]}$.For a given$p$,the difference$px-f(x)$takes the maximum at$x'$.Thus, the Legendre transformation of$f(x)$is$f^{*}(p)=px'-f(x')$.

Inmathematics,theLegendre transformation(orLegendre transform), first introduced byAdrien-Marie Legendrein 1787 when studying the minimal surface problem,is aninvolutivetransformationonreal-valued functions that areconvexon a real variable. Specifically, if a real-valued multivariable function is convex on one of its independent real variables, then the Legendre transform with respect to this variable is applicable to the function.

In physical problems, the Legendre transform is used to convert functions of one quantity (such as position, pressure, or temperature) into functions of theconjugate quantity(momentum, volume, and entropy, respectively). In this way, it is commonly used inclassical mechanicsto derive theHamiltonianformalism out of theLagrangianformalism (or vice versa) and inthermodynamicsto derive thethermodynamic potentials,as well as in the solution ofdifferential equationsof several variables.

For sufficiently smooth functions on the real line, the Legendre transform$f^{*}$of a function$f$can be specified, up to an additive constant, by the condition that the functions' first derivatives are inverse functions of each other. This can be expressed inEuler's derivative notationas $$Df(\cdot )=\left(Df^{*}\right)^{-1}(\cdot )~,$$where$D$is an operator of differentiation,$\cdot$represents an argument or input to the associated function,$(\phi )^{-1}(\cdot )$is an inverse function such that$(\phi )^{-1}(\phi (x))=x$,

or equivalently, as$f'(f^{*\prime }(x^{*}))=x^{*}$and$f^{*\prime }(f'(x))=x$inLagrange's notation.

The generalization of the Legendre transformation to affine spaces and non-convex functions is known as theconvex conjugate(also called the Legendre–Fenchel transformation), which can be used to construct a function'sconvex hull.

Definition

Definition in$\mathbb {R}$

Let$I\subset \mathbb {R}$be aninterval,and$f:I\to \mathbb {R}$aconvex function;then theLegendre transformof$f$is the function$f^{*}:I^{*}\to \mathbb {R}$defined by $$f^{*}(x^{*})=\sup _{x\in I}(x^{*}x-f(x)),\ \ \ \ I^{*}=\left\{x^{*}\in \mathbb {R}:f^{*}(x^{*})<\infty \right\}~$$ where${\textstyle \sup }$denotes thesupremumover$I$,e.g.,${\textstyle x}$in${\textstyle I}$is chosen such that${\textstyle x^{*}x-f(x)}$is maximized at each${\textstyle x^{*}}$,or${\textstyle x^{*}}$is such that$x^{*}x-f(x)$as a bounded value throughout${\textstyle x}$exists (e.g., when$f(x)$is a linear function).

The transform is always well-defined when$f(x)$isconvex.This definition requires$x^{*}x-f(x)$to bebounded from abovein$I$in order for the supremum to exist.

Definition in$\mathbb {R} ^{n}$

The generalization to convex functions$f:X\to \mathbb {R}$on aconvex set$X\subset \mathbb {R} ^{n}$is straightforward:$f^{*}:X^{*}\to \mathbb {R}$has domain $$X^{*}=\left\{x^{*}\in \mathbb {R} ^{n}:\sup _{x\in X}(\langle x^{*},x\rangle -f(x))<\infty \right\}$$ and is defined by $$f^{*}(x^{*})=\sup _{x\in X}(\langle x^{*},x\rangle -f(x)),\quad x^{*}\in X^{*}~,$$ where$\langle x^{*},x\rangle$denotes thedot productof$x^{*}$and$x$.

The function$f^{*}$is called theconvex conjugatefunction of$f$.For historical reasons (rooted in analytic mechanics), the conjugate variable is often denoted$p$,instead of$x^{*}$.If the convex function$f$is defined on the whole line and is everywheredifferentiable,then $$f^{*}(p)=\sup _{x\in I}(px-f(x))=\left(px-f(x)\right)|_{x=(f')^{-1}(p)}$$ can be interpreted as the negative of the$y$-interceptof thetangent lineto thegraphof$f$that has slope$p$.

The Legendre transformation is an application of thedualityrelationship between points and lines. The functional relationship specified by$f$can be represented equally well as a set of$(x,y)$points, or as a set of tangent lines specified by their slope and intercept values.

Understanding the Legendre transform in terms of derivatives

For a differentiable convex function$f$on the real line with the first derivative$f'$and its inverse$(f')^{-1}$,the Legendre transform of$f$,$f^{*}$,can be specified, up to an additive constant, by the condition that the functions' first derivatives are inverse functions of each other, i.e.,$f'=((f^{*})')^{-1}$and$(f^{*})'=(f')^{-1}$.

To see this, first note that if$f$as a convex function on the real line is differentiable and${\overline {x}}$is acritical pointof the function of$x\mapsto p\cdot x-f(x)$,then the supremum is achieved at${\textstyle {\overline {x}}}$(by convexity, see the first figure in this Wikipedia page). Therefore, the Legendre transform of$f$is$f^{*}(p)=p\cdot {\overline {x}}-f({\overline {x}})$.

Then, suppose that the first derivative$f'$is invertible and let the inverse be$g=(f')^{-1}$.Then for each${\textstyle p}$,the point$g(p)$is the unique critical point${\textstyle {\overline {x}}}$of the function$x\mapsto px-f(x)$(i.e.,${\overline {x}}=g(p)$) because$f'(g(p))=p$and the function's first derivative with respect to$x$at$g(p)$is$p-f'(g(p))=0$.Hence we have$f^{*}(p)=p\cdot g(p)-f(g(p))$for each${\textstyle p}$.By differentiating with respect to${\textstyle p}$,we find $$(f^{*})'(p)=g(p)+p\cdot g'(p)-f'(g(p))\cdot g'(p).$$ Since$f'(g(p))=p$this simplifies to$(f^{*})'(p)=g(p)=(f')^{-1}(p)$.In other words,$(f^{*})'$and$f'$are inverses to each other.

In general, if$h'=(f')^{-1}$as the inverse of$f',$then$h'=(f^{*})'$so integration gives$f^{*}=h+c.$with a constant$c.$

In practical terms, given$f(x),$the parametric plot of$xf'(x)-f(x)$versus$f'(x)$amounts to the graph of$f^{*}(p)$versus$p.$

In some cases (e.g. thermodynamic potentials, below), a non-standard requirement is used, amounting to an alternative definition off*with aminus sign, $$f(x)-f^{*}(p)=xp.$$

Formal Definition in Physics Context

In analytical mechanics and thermodynamics, Legendre transformation is usually defined as follows: suppose$f$is a function of$x,$then we have

$\mathrm {d} f={\frac {\mathrm {d} f}{\mathrm {d} x}}\mathrm {d} x.$

performing Legendre transformation on this function means that we take$p={\frac {\mathrm {d} f}{\mathrm {d} x}}$as the independent variable, so that the above expression can be written as

$\mathrm {d} f=p\mathrm {d} x,$

and according to Leibniz's rule$\mathrm {d} (uv)=u\mathrm {d} v+v\mathrm {d} u,$then we have

$\mathrm {d} \left(xp-f\right)=x\mathrm {d} p,$

and taking$f^{*}=xp-f,$we have$\mathrm {d} f^{*}=x\mathrm {d} p,$which means

${\frac {\mathrm {d} f^{*}}{\mathrm {d} p}}=x.$

When$f$is a function of$n$variables$x_{1},x_{2},\cdots,x_{n}$,then we can perform the Legendre transformation on each one or several variables: we have

$\mathrm {d} f=p_{1}\mathrm {d} x_{1}+p_{2}\mathrm {d} x_{2}+\cdots +p_{n}\mathrm {d} x_{n}$

where$p_{i}={\frac {\partial f}{\partial x_{i}}}.$Then if we want to perform Legendre transformation on, e.g.$x_{1}$then we take$p_{1}$together with$x_{2},\cdots,x_{n}$as independent variables, and with Leibniz's rule we have

$\mathrm {d} (f-x_{1}p_{1})=-x_{1}\mathrm {d} p_{1}+p_{2}\mathrm {d} x_{2}+\cdots +p_{n}\mathrm {d} x_{n}.$

so for function$\varphi (p_{1},x_{2},\cdots,x_{n})=f(x_{1},x_{2},\cdots,x_{n})-x_{1}p_{1},$we have

${\frac {\partial \varphi }{\partial p_{1}}}=-x_{1},\quad {\frac {\partial \varphi }{\partial x_{2}}}=p_{2},\quad \cdots,\quad {\frac {\partial \varphi }{\partial x_{n}}}=p_{n}.$

We can also do this transformation for variables$x_{2},\cdots,x_{n}$.If we do it to all the variables, then we have

$\mathrm {d} \varphi =-x_{1}\mathrm {d} p_{1}-x_{2}\mathrm {d} p_{2}-\cdots -x_{n}\mathrm {d} p_{n}$where$\varphi =f-x_{1}p_{1}-x_{2}p_{2}-\cdots -x_{n}p_{n}.$

In analytical mechanics, people perform this transformation on variables${\dot {q}}_{1},{\dot {q}}_{2},\cdots,{\dot {q}}_{n}$of the Lagrangian$L(q_{1},\cdots,q_{n},{\dot {q}}_{1},\cdots,{\dot {q}}_{n})$to get the Hamiltonian:

$H(q_{1},\cdots,q_{n},p_{1},\cdots,p_{n})=\sum _{i=1}^{n}p_{i}{\dot {q}}_{i}-L(q_{1},\cdots,q_{n},{\dot {q}}_{1}\cdots,{\dot {q}}_{n})$

and in thermodynamics, people perform this transformation on variables according to the type of thermodynamic system they want. E.g. starting from the cardinal function of state, the internal energy$U(S,V)$,we have

$\mathrm {d} U=T\mathrm {d} S-p\mathrm {d} V,$

we can perform Legendre transformation on either or both of$S,V$yielding

$\mathrm {d} H=\mathrm {d} (U+pV)\ \ \ \ \ \ \ \ \ \ =\ \ \ \ T\mathrm {d} S+V\mathrm {d} p$

$\mathrm {d} F=\mathrm {d} (U-TS)\ \ \ \ \ \ \ \ \ \ =-S\mathrm {d} T-p\mathrm {d} V$

$\mathrm {d} G=\mathrm {d} (U-TS+pV)=-S\mathrm {d} T+V\mathrm {d} p$

and each of these three expressions has a physical meaning.

This definition of Legendre transformation is the one originally introduced by Legendre in his work in 1787,and still applied by physicists nowadays. Indeed, this definition can be mathematically rigorous if we treat all the variables and functions defined above, e.g.$f,x_{1},\cdots,x_{n},p_{1},\cdots,p_{n},$as differentiable functions defined on an open set of$\mathbb {R} ^{n}$or on a differentiable manifold, and$\mathrm {d} f,\mathrm {d} x_{i},\mathrm {d} p_{i}$their differentials (which are treated as cotangent vector field in the context of differentiable manifold). And this definition is equivalent to the modern mathematicians' definition as long as$f$is differentiable and convex for the variables$x_{1},x_{2},\cdots,x_{n}.$

Properties

• The Legendre transform of a convex function, of which double derivative values are all positive, is also a convex function of which double derivative values are all positive.
  Proof.Let us show this with a doubly differentiable function$f(x)$with all positive double derivative values and with a bijective (invertible) derivative.
  For a fixed$p$,let${\bar {x}}$maximize or make the function$px-f(x)$bounded over$x$.Then the Legendre transformation of$f$is$f^{*}(p)=p{\bar {x}}-f({\bar {x}})$,thus,$$f'({\bar {x}})=p$$by the maximizing or bounding condition${\frac {d}{dx}}(px-f(x))=p-f'(x)=0$.Note that${\bar {x}}$depends on$p$.(This can be visually shown in the 1st figure of this page above.)
  Thus${\bar {x}}=g(p)$where$g\equiv (f')^{-1}$,meaning that$g$is the inverse of$f'$that is the derivative of$f$(so$f'(g(p))=p$).
  Note that$g$is also differentiable with thefollowing derivative (Inverse function rule),$${\frac {dg(p)}{dp}}={\frac {1}{f''(g(p))}}~.$$Thus, the Legendre transformation$f^{*}(p)=pg(p)-f(g(p))$is the composition of differentiable functions, hence it is differentiable.
  Applying theproduct ruleand thechain rulewith the found equality${\bar {x}}=g(p)$yields$${\frac {d(f^{*})}{dp}}=g(p)+\left(p-f'(g(p))\right)\cdot {\frac {dg(p)}{dp}}=g(p),$$giving$${\frac {d^{2}(f^{*})}{dp^{2}}}={\frac {dg(p)}{dp}}={\frac {1}{f''(g(p))}}>0,$$so$f^{*}$is convex with its double derivatives are all positive.
• The Legendre transformation is aninvolution,i.e.,$f^{**}=f~$.
  Proof.By using the above identities as$f'({\bar {x}})=p$,${\bar {x}}=g(p)$,$f^{*}(p)=p{\bar {x}}-f({\bar {x}})$and its derivative$(f^{*})'(p)=g(p)$,$${\begin{aligned}f^{**}(y)&{}=\left(y\cdot {\bar {p}}-f^{*}({\bar {p}})\right)|_{(f^{*})'({\bar {p}})=y}\\[5pt]&{}=g({\bar {p}})\cdot {\bar {p}}-f^{*}({\bar {p}})\\[5pt]&{}=g({\bar {p}})\cdot {\bar {p}}-({\bar {p}}g({\bar {p}})-f(g({\bar {p}})))\\[5pt]&{}=f(g({\bar {p}}))\\[5pt]&{}=f(y)~.\end{aligned}}$$Note that this derivation does not require the condition to have all positive values in double derivative of the original function$f$.

Identities

As shownabove,for a convex function$f(x)$,with$x={\bar {x}}$maximizing or making$px-f(x)$bounded at each$p$to define the Legendre transform$f^{*}(p)=p{\bar {x}}-f({\bar {x}})$and with$g\equiv (f')^{-1}$,the following identities hold.

• $f'({\bar {x}})=p$,
• ${\bar {x}}=g(p)$,
• $(f^{*})'(p)=g(p)$.

Examples

Example 1

$f(x)=e^{x}$over the domain$I=\mathbb {R}$is plotted in red and its Legendre transform$f^{*}(x^{*})=x^{*}(\ln(x^{*})-1)$over the domain$I^{*}=(0,\infty )$in dashed blue. Note that the Legendre transform appears convex.

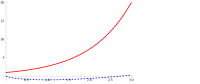
Consider theexponential function$f(x)=e^{x},$which has the domain$I=\mathbb {R}$.From the definition, the Legendre transform is $$f^{*}(x^{*})=\sup _{x\in \mathbb {R} }(x^{*}x-e^{x}),\quad x^{*}\in I^{*}$$ where$I^{*}$remains to be determined. To evaluate thesupremum,compute the derivative of$x^{*}x-e^{x}$with respect to$x$and set equal to zero: $${\frac {d}{dx}}(x^{*}x-e^{x})=x^{*}-e^{x}=0.$$ Thesecond derivative$-e^{x}$is negative everywhere, so the maximal value is achieved at$x=\ln(x^{*})$.Thus, the Legendre transform is $$f^{*}(x^{*})=x^{*}\ln(x^{*})-e^{\ln(x^{*})}=x^{*}(\ln(x^{*})-1)$$ and has domain$I^{*}=(0,\infty ).$This illustrates that thedomainsof a function and its Legendre transform can be different.

To find the Legendre transformation of the Legendre transformation of$f$, $$f^{**}(x)=\sup _{x^{*}\in \mathbb {R} }(xx^{*}-x^{*}(\ln(x^{*})-1)),\quad x\in I,$$ where a variable$x$is intentionally used as the argument of the function$f^{**}$to show theinvolutionproperty of the Legendre transform as$f^{**}=f$.we compute $${\begin{aligned}0&={\frac {d}{dx^{*}}}{\big (}xx^{*}-x^{*}(\ln(x^{*})-1){\big )}=x-\ln(x^{*})\end{aligned}}$$ thus the maximum occurs at$x^{*}=e^{x}$because the second derivative${\frac {d^{2}}{{dx^{*}}^{2}}}f^{**}(x)=-{\frac {1}{x^{*}}}<0$over the domain of$f^{**}$as$I^{*}=(0,\infty ).$As a result,$f^{**}$is found as $${\begin{aligned}f^{**}(x)&=xe^{x}-e^{x}(\ln(e^{x})-1)=e^{x},\end{aligned}}$$ thereby confirming that$f=f^{**},$as expected.

Example 2

Letf(x) =cx²defined onR,wherec> 0is a fixed constant.

Forx*fixed, the function ofx,x*x−f(x) =x*x−cx²has the first derivativex* − 2cxand second derivative−2c;there is one stationary point atx=x*/2c,which is always a maximum.

Thus,I* =Rand $$f^{*}(x^{*})={\frac {{x^{*}}^{2}}{4c}}~.$$

The first derivatives off,2cx,and off*,x*/(2c),are inverse functions to each other. Clearly, furthermore, $$f^{**}(x)={\frac {1}{4(1/4c)}}x^{2}=cx^{2}~,$$ namelyf** =f.

Example 3

Letf(x) =x²forx∈ (I= [2, 3]).

Forx*fixed,x*x−f(x)is continuous onIcompact,hence it always takes a finite maximum on it; it follows that the domain of the Legendre transform of$f$isI* =R.

The stationary point atx=x*/2(found by setting that the first derivative ofx*x−f(x)with respect to$x$equal to zero) is in the domain[2, 3]if and only if4 ≤x* ≤ 6.Otherwise the maximum is taken either atx= 2orx= 3because the second derivative ofx*x−f(x)with respect to$x$is negative as$-2$;for a part of the domain$x^{*}<4$the maximum thatx*x−f(x)can take with respect to$x\in [2,3]$is obtained at$x=2$while for$x^{*}>6$it becomes the maximum at$x=3$.Thus, it follows that $$f^{*}(x^{*})={\begin{cases}2x^{*}-4,&x^{*}<4\\{\frac {{x^{*}}^{2}}{4}},&4\leq x^{*}\leq 6,\\3x^{*}-9,&x^{*}>6.\end{cases}}$$

Example 4

The functionf(x) =cxis convex, for everyx(strict convexity is not required for the Legendre transformation to be well defined). Clearlyx*x−f(x) = (x* −c)xis neverbounded from aboveas a function ofx,unlessx* −c= 0.Hencef*is defined onI* = {c}andf*(c) = 0.(The definition of the Legendre transformrequires the existence of thesupremum,that requires upper bounds.)

One may check involutivity: of course,x*x−f*(x*)is always bounded as a function ofx*∈{c},henceI** =R.Then, for allxone has $$\sup _{x^{*}\in \{c\}}(xx^{*}-f^{*}(x^{*}))=xc,$$ and hencef**(x) =cx=f(x).

Example 5

As an example of a convex continuous function that is not everywhere differentiable, consider$f(x)=|x|$.This gives$$f^{*}(x^{*})=\sup _{x}(xx^{*}-|x|)=\max \left(\sup _{x\geq 0}x(x^{*}-1),\,\sup _{x\leq 0}x(x^{*}+1)\right),$$and thus$f^{*}(x^{*})=0$on its domain$I^{*}=[-1,1]$.

Example 6: several variables

Let $$f(x)=\langle x,Ax\rangle +c$$ be defined onX=Rⁿ,whereAis a real, positive definite matrix.

Thenfis convex, and $$\langle p,x\rangle -f(x)=\langle p,x\rangle -\langle x,Ax\rangle -c,$$ has gradientp− 2AxandHessian−2A,which is negative; hence the stationary pointx=A⁻¹p/2is a maximum.

We haveX* =Rⁿ,and $$f^{*}(p)={\frac {1}{4}}\langle p,A^{-1}p\rangle -c.$$

Behavior of differentials under Legendre transforms

The Legendre transform is linked tointegration by parts,p dx=d(px) −x dp.

Letf(x,y)be a function of two independent variablesxandy,with the differential $$df={\frac {\partial f}{\partial x}}\,dx+{\frac {\partial f}{\partial y}}\,dy=p\,dx+v\,dy.$$

Assume that the functionfis convex inxfor ally,so that one may perform the Legendre transform onfinx,withpthe variable conjugate tox(for information, there is a relation${\frac {\partial f}{\partial x}}|_{\bar {x}}=p$where${\bar {x}}$is a point inxmaximizing or making$px-f(x,y)$bounded for givenpandy). Since the new independent variable of the transform with respect tofisp,the differentialsdxanddyindfdevolve todpanddyin the differential of the transform, i.e., we build another function with its differential expressed in terms of the new basisdpanddy.

We thus consider the functiong(p,y) =f−pxso that $$dg=df-p\,dx-x\,dp=-x\,dp+v\,dy$$ $$x=-{\frac {\partial g}{\partial p}}$$ $$v={\frac {\partial g}{\partial y}}.$$

The function−g(p,y)is the Legendre transform off(x,y),where only the independent variablexhas been supplanted byp.This is widely used inthermodynamics,as illustrated below.

Applications

Analytical mechanics

A Legendre transform is used inclassical mechanicsto derive theHamiltonian formulationfrom theLagrangian formulation,and conversely. A typical Lagrangian has the form

$$L(v,q)={\tfrac {1}{2}}\langle v,Mv\rangle -V(q),$$ where$(v,q)$are coordinates onRⁿ×Rⁿ,Mis a positive definite real matrix, and $$\langle x,y\rangle =\sum _{j}x_{j}y_{j}.$$

For everyqfixed,$L(v,q)$is a convex function of$v$,while$V(q)$plays the role of a constant.

Hence the Legendre transform of$L(v,q)$as a function of$v$is the Hamiltonian function, $$H(p,q)={\tfrac {1}{2}}\langle p,M^{-1}p\rangle +V(q).$$

In a more general setting,$(v,q)$are local coordinates on thetangent bundle$T{\mathcal {M}}$of a manifold${\mathcal {M}}$.For eachq,$L(v,q)$is a convex function of the tangent spaceV_q.The Legendre transform gives the Hamiltonian$H(p,q)$as a function of the coordinates(p,q)of thecotangent bundle$T^{*}{\mathcal {M}}$;the inner product used to define the Legendre transform is inherited from the pertinent canonicalsymplectic structure.In this abstract setting, the Legendre transformation corresponds to thetautological one-form.

Thermodynamics

The strategy behind the use of Legendre transforms in thermodynamics is to shift from a function that depends on a variable to a new (conjugate) function that depends on a new variable, the conjugate of the original one. The new variable is the partial derivative of the original function with respect to the original variable. The new function is the difference between the original function and the product of the old and new variables. Typically, this transformation is useful because it shifts the dependence of, e.g., the energy from anextensive variableto its conjugate intensive variable, which can often be controlled more easily in a physical experiment.

For example, theinternal energyUis an explicit function of theextensive variablesentropyS,volumeV,andchemical compositionN_i(e.g.,$i=1,2,3,\ldots$) $$U=U\left(S,V,\{N_{i}\}\right),$$ which has a total differential $$dU=T\,dS-P\,dV+\sum \mu _{i}\,dN_{i}$$

where$T=\left.{\frac {\partial U}{\partial S}}\right\vert _{V,N_{i\ for\ all\ i\ values}},P=\left.-{\frac {\partial U}{\partial V}}\right\vert _{S,N_{i\ for\ all\ i\ values}},\mu _{i}=\left.{\frac {\partial U}{\partial N_{i}}}\right\vert _{S,V,N_{j\ for\ all\ j\neq i}}$.

(Subscripts are not necessary by the definition of partial derivatives but left here for clarifying variables.) Stipulating some common reference state, by using the (non-standard) Legendre transform of the internal energyUwith respect to volumeV,theenthalpyHmay be obtained as the following.

To get the (standard) Legendre transform${\textstyle U^{*}}$of the internal energyUwith respect to volumeV,the function${\textstyle u\left(p,S,V,\{{{N}_{i}}\}\right)=pV-U}$is defined first, then it shall be maximized or bounded byV.To do this, the condition${\textstyle {\frac {\partial u}{\partial V}}=p-{\frac {\partial U}{\partial V}}=0\to p={\frac {\partial U}{\partial V}}}$needs to be satisfied, so${\textstyle U^{*}={\frac {\partial U}{\partial V}}V-U}$is obtained. This approach is justified becauseUis a linear function with respect toV(so a convex function onV) by the definition ofextensive variables.The non-standard Legendre transform here is obtained by negating the standard version, so${\textstyle -U^{*}=H=U-{\frac {\partial U}{\partial V}}V=U+PV}$.

His definitely astate functionas it is obtained by addingPV(PandVasstate variables) to a state function${\textstyle U=U\left(S,V,\{N_{i}\}\right)}$,so its differential is anexact differential.Because of${\textstyle dH=T\,dS+V\,dP+\sum \mu _{i}\,dN_{i}}$and the fact that it must be an exact differential,$H=H(S,P,\{N_{i}\})$.

The enthalpy is suitable for description of processes in which the pressure is controlled from the surroundings.

It is likewise possible to shift the dependence of the energy from the extensive variable of entropy,S,to the (often more convenient) intensive variableT,resulting in theHelmholtzandGibbsfree energies.The Helmholtz free energyA,and Gibbs energyG,are obtained by performing Legendre transforms of the internal energy and enthalpy, respectively, $$A=U-TS~,$$$$G=H-TS=U+PV-TS~.$$

The Helmholtz free energy is often the most useful thermodynamic potential when temperature and volume are controlled from the surroundings, while the Gibbs energy is often the most useful when temperature and pressure are controlled from the surroundings.

Variable capacitor

As another example fromphysics,consider a parallel conductive platecapacitor,in which the plates can move relative to one another. Such a capacitor would allow transfer of the electric energy which is stored in the capacitor into external mechanical work, done by theforceacting on the plates. One may think of the electric charge as analogous to the "charge" of agasin acylinder,with the resulting mechanicalforceexerted on apiston.

Compute the force on the plates as a function ofx,the distance which separates them. To find the force, compute the potential energy, and then apply the definition of force as the gradient of the potential energy function.

Theelectrostatic potential energystored in a capacitor of thecapacitanceC(x)and a positiveelectric charge+Qor negative charge-Qon each conductive plate is (with using the definition of the capacitance as${\textstyle C={\frac {Q}{V}}}$),

$$U(Q,\mathbf {x} )={\frac {1}{2}}QV(Q,\mathbf {x} )={\frac {1}{2}}{\frac {Q^{2}}{C(\mathbf {x} )}},~$$

where the dependence on the area of the plates, the dielectric constant of the insulation material between the plates, and the separationxare abstracted away as thecapacitanceC(x).(For a parallel plate capacitor, this is proportional to the area of the plates and inversely proportional to the separation.)

The forceFbetween the plates due to the electric field created by the charge separation is then $$\mathbf {F} (\mathbf {x} )=-{\frac {dU}{d\mathbf {x} }}~.$$

If the capacitor is not connected to any electric circuit, then theelectric chargeson the plates remain constant and the voltage varies when the plates move with respect to each other, and the force is the negativegradientof theelectrostaticpotential energy as $$\mathbf {F} (\mathbf {x} )={\frac {1}{2}}{\frac {dC(\mathbf {x} )}{d\mathbf {x} }}{\frac {Q^{2}}{{C(\mathbf {x} )}^{2}}}={\frac {1}{2}}{\frac {dC(\mathbf {x} )}{d\mathbf {x} }}V(\mathbf {x} )^{2}$$

where${\textstyle V(Q,\mathbf {x} )=V(\mathbf {x} )}$as the charge is fixed in this configuration.

However, instead, suppose that thevoltagebetween the platesVis maintained constant as the plate moves by connection to abattery,which is a reservoir for electric charges at a constant potential difference. Then the amount ofcharges${\textstyle Q}$is a variableinstead of the voltage;${\textstyle Q}$and${\textstyle V}$are the Legendre conjugate to each other. To find the force, first compute the non-standard Legendre transform${\textstyle U^{*}}$with respect to${\textstyle Q}$(also with using${\textstyle C={\frac {Q}{V}}}$),

$$U^{*}=U-\left.{\frac {\partial U}{\partial Q}}\right|_{\mathbf {x} }\cdot Q=U-{\frac {1}{2C(\mathbf {x} )}}\left.{\frac {\partial Q^{2}}{\partial Q}}\right|_{\mathbf {x} }\cdot Q=U-QV={\frac {1}{2}}QV-QV=-{\frac {1}{2}}QV=-{\frac {1}{2}}V^{2}C(\mathbf {x} ).$$

This transformation is possible because${\textstyle U}$is now a linear function of${\textstyle Q}$so is convex on it. The force now becomes the negative gradient of this Legendre transform, resulting in the same force obtained from the original function${\textstyle U}$, $$\mathbf {F} (\mathbf {x} )=-{\frac {dU^{*}}{d\mathbf {x} }}={\frac {1}{2}}{\frac {dC(\mathbf {x} )}{d\mathbf {x} }}V^{2}.$$

The two conjugate energies${\textstyle U}$and${\textstyle U^{*}}$happen to stand opposite to each other (their signs are opposite), only because of thelinearityof thecapacitance—except nowQis no longer a constant. They reflect the two different pathways of storing energy into the capacitor, resulting in, for instance, the same "pull" between a capacitor's plates.

Probability theory

Inlarge deviations theory,therate functionis defined as the Legendre transformation of the logarithm of themoment generating functionof a random variable. An important application of the rate function is in the calculation of tail probabilities of sums ofi.i.d. random variables,in particular inCramér's theorem.

If$X_{n}$are i.i.d. random variables, let$S_{n}=X_{1}+\cdots +X_{n}$be the associatedrandom walkand$M(\xi )$the moment generating function of$X_{1}$.For$\xi \in \mathbb {R}$,$E[e^{\xi S_{n}}]=M(\xi )^{n}$.Hence, byMarkov's inequality,one has for$\xi \geq 0$and$a\in \mathbb {R}$ $$P(S_{n}/n>a)\leq e^{-n\xi a}M(\xi )^{n}=\exp[-n(\xi a-\Lambda (\xi ))]$$ where$\Lambda (\xi )=\log M(\xi )$.Since the left-hand side is independent of$\xi$,we may take the infimum of the right-hand side, which leads one to consider the supremum of$\xi a-\Lambda (\xi )$,i.e., the Legendre transform of$\Lambda$,evaluated at$x=a$.

Microeconomics

Legendre transformation arises naturally inmicroeconomicsin the process of finding thesupplyS(P)of some product given a fixed pricePon the market knowing thecost functionC(Q),i.e. the cost for the producer to make/mine/etc.Qunits of the given product.

A simple theory explains the shape of the supply curve based solely on the cost function. Let us suppose the market price for a one unit of our product isP.For a company selling this good, the best strategy is to adjust the productionQso that its profit is maximized. We can maximize the profit $${\text{profit}}={\text{revenue}}-{\text{costs}}=PQ-C(Q)$$ by differentiating with respect toQand solving $$P-C'(Q_{\text{opt}})=0.$$

Q_optrepresents the optimal quantityQof goods that the producer is willing to supply, which is indeed the supply itself: $$S(P)=Q_{\text{opt}}(P)=(C')^{-1}(P).$$

If we consider the maximal profit as a function of price,${\text{profit}}_{\text{max}}(P)$,we see that it is the Legendre transform of the cost function$C(Q)$.

Geometric interpretation

For astrictly convex function,the Legendre transformation can be interpreted as a mapping between thegraphof the function and the family oftangentsof the graph. (For a function of one variable, the tangents are well-defined at all but at mostcountably manypoints, since a convex function isdifferentiableat all but at most countably many points.)

The equation of a line withslope$p$and$y$-intercept$b$is given by$y=px+b$.For this line to be tangent to the graph of a function$f$at the point$\left(x_{0},f(x_{0})\right)$requires $$f(x_{0})=px_{0}+b$$ and $$p=f'(x_{0}).$$

Being the derivative of a strictly convex function, the function$f'$is strictly monotone and thusinjective.The second equation can be solved for${\textstyle x_{0}=f^{\prime -1}(p),}$allowing elimination of$x_{0}$from the first, and solving for the$y$-intercept$b$of the tangent as a function of its slope$p,$${\textstyle b=f(x_{0})-px_{0}=f\left(f^{\prime -1}(p)\right)-p\cdot f^{\prime -1}(p)=-f^{\star }(p)}$where$f^{\star }$denotes the Legendre transform of$f.$

Thefamilyof tangent lines of the graph of$f$parameterized by the slope$p$is therefore given by ${\textstyle y=px-f^{\star }(p),}$or, written implicitly, by the solutions of the equation $$F(x,y,p)=y+f^{\star }(p)-px=0~.$$

The graph of the original function can be reconstructed from this family of lines as theenvelopeof this family by demanding $${\frac {\partial F(x,y,p)}{\partial p}}=f^{\star \prime }(p)-x=0.$$

Eliminating$p$from these two equations gives $$y=x\cdot f^{\star \prime -1}(x)-f^{\star }\left(f^{\star \prime -1}(x)\right).$$

Identifying$y$with$f(x)$and recognizing the right side of the preceding equation as the Legendre transform of$f^{\star },$yield${\textstyle f(x)=f^{\star \star }(x)~.}$

Legendre transformation in more than one dimension

For a differentiable real-valued function on anopenconvex subsetUofRⁿthe Legendre conjugate of the pair(U,f)is defined to be the pair(V,g),whereVis the image ofUunder thegradientmappingDf,andgis the function onVgiven by the formula $$g(y)=\left\langle y,x\right\rangle -f(x),\qquad x=\left(Df\right)^{-1}(y)$$ where $$\left\langle u,v\right\rangle =\sum _{k=1}^{n}u_{k}\cdot v_{k}$$

is thescalar productonRⁿ.The multidimensional transform can be interpreted as an encoding of theconvex hullof the function'sepigraphin terms of itssupporting hyperplanes.This can be seen as consequence of the following two observations. On the one hand, the hyperplane tangent to the epigraph of$f$at some point$(\mathbf {x},f(\mathbf {x} ))\in U\times \mathbb {R}$has normal vector$(\nabla f(\mathbf {x} ),-1)\in \mathbb {R} ^{n+1}$.On the other hand, any closed convex set$C\in \mathbb {R} ^{m}$can be characterized via the set of itssupporting hyperplanesby the equations$\mathbf {x} \cdot \mathbf {n} =h_{C}(\mathbf {n} )$,where$h_{C}(\mathbf {n} )$is thesupport functionof$C$.But the definition of Legendre transform via the maximization matches precisely that of the support function, that is,$f^{*}(\mathbf {x} )=h_{\operatorname {epi} (f)}(\mathbf {x},-1)$.We thus conclude that the Legendre transform characterizes the epigraph in the sense that the tangent plane to the epigraph at any point$(\mathbf {x},f(\mathbf {x} ))$is given explicitly by$$\{\mathbf {z} \in \mathbb {R} ^{n+1}:\,\,\mathbf {z} \cdot \mathbf {x} =f^{*}(\mathbf {x} )\}.$$

Alternatively, ifXis avector spaceandYis itsdual vector space,then for each pointxofXandyofY,there is a natural identification of thecotangent spacesT*X_xwithYandT*Y_ywithX.Iffis a real differentiable function overX,then itsexterior derivative,df,is a section of thecotangent bundleT*Xand as such, we can construct a map fromXtoY.Similarly, ifgis a real differentiable function overY,thendgdefines a map fromYtoX.If both maps happen to be inverses of each other, we say we have a Legendre transform. The notion of thetautological one-formis commonly used in this setting.

When the function is not differentiable, the Legendre transform can still be extended, and is known as theLegendre-Fenchel transformation.In this more general setting, a few properties are lost: for example, the Legendre transform is no longer its own inverse (unless there are extra assumptions, likeconvexity).

Legendre transformation on manifolds

Let${\textstyle M}$be asmooth manifold,let$E$and${\textstyle \pi:E\to M}$be avector bundleon$M$and its associatedbundle projection,respectively. Let${\textstyle L:E\to \mathbb {R} }$be a smooth function. We think of${\textstyle L}$as aLagrangianby analogy with the classical case where${\textstyle M=\mathbb {R} }$,${\textstyle E=TM=\mathbb {R} \times \mathbb {R} }$and${\textstyle L(x,v)={\frac {1}{2}}mv^{2}-V(x)}$for some positive number${\textstyle m\in \mathbb {R} }$and function${\textstyle V:M\to \mathbb {R} }$.

As usual, thedualof${\textstyle E}$is denote by${\textstyle E^{*}}$.The fiber of${\textstyle \pi }$over${\textstyle x\in M}$is denoted${\textstyle E_{x}}$,and the restriction of${\textstyle L}$to${\textstyle E_{x}}$is denoted by${\textstyle L|_{E_{x}}:E_{x}\to \mathbb {R} }$.TheLegendre transformationof${\textstyle L}$is the smooth morphism$$\mathbf {F} L:E\to E^{*}$$defined by${\textstyle \mathbf {F} L(v)=d(L|_{E_{x}})_{v}\in E_{x}^{*}}$,where${\textstyle x=\pi (v)}$.Here we use the fact that since${\textstyle E_{x}}$is a vector space,${\textstyle T_{v}(E_{x})}$can be identified with${\textstyle E_{x}}$. In other words,${\textstyle \mathbf {F} L(v)\in E_{x}^{*}}$is the covector that sends${\textstyle w\in E_{x}}$to the directional derivative${\textstyle \left.{\frac {d}{dt}}\right|_{t=0}L(v+tw)\in \mathbb {R} }$.

To describe the Legendre transformation locally, let${\textstyle U\subseteq M}$be a coordinate chart over which${\textstyle E}$is trivial. Picking a trivialization of${\textstyle E}$over${\textstyle U}$,we obtain charts${\textstyle E_{U}\cong U\times \mathbb {R} ^{r}}$and${\textstyle E_{U}^{*}\cong U\times \mathbb {R} ^{r}}$.In terms of these charts, we have${\textstyle \mathbf {F} L(x;v_{1},\dotsc,v_{r})=(x;p_{1},\dotsc,p_{r})}$,where$$p_{i}={\frac {\partial L}{\partial v_{i}}}(x;v_{1},\dotsc,v_{r})$$for all${\textstyle i=1,\dots,r}$.If, as in the classical case, the restriction of${\textstyle L:E\to \mathbb {R} }$to each fiber${\textstyle E_{x}}$is strictly convex and bounded below by a positive definite quadratic form minus a constant, then the Legendre transform${\textstyle \mathbf {F} L:E\to E^{*}}$is a diffeomorphism.Suppose that${\textstyle \mathbf {F} L}$is a diffeomorphism and let${\textstyle H:E^{*}\to \mathbb {R} }$be the "Hamiltonian"function defined by$$H(p)=p\cdot v-L(v),$$where${\textstyle v=(\mathbf {F} L)^{-1}(p)}$.Using the natural isomorphism${\textstyle E\cong E^{**}}$,we may view the Legendre transformation of${\textstyle H}$as a map${\textstyle \mathbf {F} H:E^{*}\to E}$.Then we have$$(\mathbf {F} L)^{-1}=\mathbf {F} H.$$

Further properties

Scaling properties

The Legendre transformation has the following scaling properties: Fora> 0,

$$f(x)=a\cdot g(x)\Rightarrow f^{\star }(p)=a\cdot g^{\star }\left({\frac {p}{a}}\right)$$ $$f(x)=g(a\cdot x)\Rightarrow f^{\star }(p)=g^{\star }\left({\frac {p}{a}}\right).$$

It follows that if a function ishomogeneous of degreerthen its image under the Legendre transformation is a homogeneous function of degrees,where1/r+ 1/s= 1.(Sincef(x) =x^r/r,withr> 1,impliesf*(p) =p^s/s.) Thus, the only monomial whose degree is invariant under Legendre transform is the quadratic.

Behavior under translation

$$f(x)=g(x)+b\Rightarrow f^{\star }(p)=g^{\star }(p)-b$$ $$f(x)=g(x+y)\Rightarrow f^{\star }(p)=g^{\star }(p)-p\cdot y$$

Behavior under inversion

$$f(x)=g^{-1}(x)\Rightarrow f^{\star }(p)=-p\cdot g^{\star }\left({\frac {1}{p}}\right)$$

Behavior under linear transformations

LetA:Rⁿ→R^mbe alinear transformation.For any convex functionfonRⁿ,one has $$(Af)^{\star }=f^{\star }A^{\star }$$ whereA*is theadjoint operatorofAdefined by $$\left\langle Ax,y^{\star }\right\rangle =\left\langle x,A^{\star }y^{\star }\right\rangle,$$ andAfis thepush-forwardoffalongA $$(Af)(y)=\inf\{f(x):x\in X,Ax=y\}.$$

A closed convex functionfis symmetric with respect to a given setGoforthogonal linear transformations, $$f(Ax)=f(x),\;\forall x,\;\forall A\in G$$ if and only iff*is symmetric with respect toG.

Infimal convolution

Theinfimal convolutionof two functionsfandgis defined as

$$\left(f\star _{\inf }g\right)(x)=\inf \left\{f(x-y)+g(y)\,|\,y\in \mathbf {R} ^{n}\right\}.$$

Letf₁,...,f_mbe proper convex functions onRⁿ.Then

$$\left(f_{1}\star _{\inf }\cdots \star _{\inf }f_{m}\right)^{\star }=f_{1}^{\star }+\cdots +f_{m}^{\star }.$$

Fenchel's inequality

For any functionfand its convex conjugatef*Fenchel's inequality(also known as theFenchel–Young inequality) holds for everyx∈Xandp∈X*,i.e.,independentx,ppairs, $$\left\langle p,x\right\rangle \leq f(x)+f^{\star }(p).$$

See also

• Dual curve
• Projective duality
• Young's inequality for products
• Convex conjugate
• Moreau's theorem
• Integration by parts
• Fenchel's duality theorem

References

• Courant, Richard;Hilbert, David(2008).Methods of Mathematical Physics.Vol. 2. John Wiley & Sons.ISBN978-0471504399.
• Arnol'd, Vladimir Igorevich(1989).Mathematical Methods of Classical Mechanics(2nd ed.). Springer.ISBN0-387-96890-3.
• Fenchel, W. (1949). "On conjugate convex functions",Can. J. Math1:73-77.
• Rockafellar, R. Tyrrell(1996) [1970].Convex Analysis.Princeton University Press.ISBN0-691-01586-4.
• Zia, R. K. P.; Redish, E. F.; McKay, S. R. (2009). "Making sense of the Legendre transform".American Journal of Physics.77(7): 614.arXiv:0806.1147.Bibcode:2009AmJPh..77..614Z.doi:10.1119/1.3119512.S2CID37549350.

Further reading

• Nielsen, Frank (2010-09-01)."Legendre transformation and information geometry"(PDF).Retrieved2016-01-24.
• Touchette, Hugo (2005-07-27)."Legendre-Fenchel transforms in a nutshell"(PDF).Retrieved2016-01-24.
• Touchette, Hugo (2006-11-21)."Elements of convex analysis"(PDF).Archived fromthe original(PDF)on 2016-02-01.Retrieved2016-01-24.

External links

• Legendre transform with figuresat maze5.net
• Legendre and Legendre-Fenchel transforms in a step-by-step explanationat onmyphd.com