Matrix (mathematics)

"Matrix theory" redirects here. For the physics topic, seeMatrix theory (physics).For other uses of "Matrix", seeMatrix (disambiguation).

Anm×nmatrix: themrows are horizontal and thencolumns are vertical. Each element of a matrix is often denoted by a variable with twosubscripts.For example,a_2,1represents the element at the second row and first column of the matrix.

Inmathematics,amatrix(pl.:matrices) is arectangulararray or table ofnumbers,symbols,orexpressions,with elements or entries arranged in rows and columns, which is used to represent amathematical objector property of such an object.

For example, $${\begin{bmatrix}1&9&-13\\20&5&-6\end{bmatrix}}$$ is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a "$2\times 3$matrix ", or a matrix of dimension$2\times 3$.

Matrices are commonly related tolinear algebra.Notable exceptions includeincidence matricesandadjacency matricesingraph theory.This article focuses on matrices related to linear algebra, and, unless otherwise specified, all matrices representlinear mapsor may be viewed as such.

Square matrices,matrices with the same number of rows and columns, play a major role in matrix theory. Square matrices of a given dimension form anoncommutative ring,which is one of the most common examples of a noncommutative ring. Thedeterminantof a square matrix is a number associated with the matrix, which is fundamental for the study of a square matrix; for example, a square matrix isinvertibleif and only if it has a nonzero determinant and theeigenvaluesof a square matrix are the roots of apolynomialdeterminant.

Ingeometry,matrices are widely used for specifying and representinggeometric transformations(for examplerotations) andcoordinate changes.Innumerical analysis,many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions. Matrices are used in most areas of mathematics and scientific fields, either directly, or through their use in geometry and numerical analysis.

Matrix theoryis thebranch of mathematicsthat focuses on the study of matrices. It was initially a sub-branch oflinear algebra,but soon grew to include subjects related tograph theory,algebra,combinatoricsandstatistics.

Definition

Amatrixis a rectangular array ofnumbers(or other mathematical objects), called theentriesof the matrix. Matrices are subject to standardoperationssuch asadditionandmultiplication.Most commonly, a matrix over afieldFis a rectangular array ofelementsofF.Areal matrixand acomplex matrixare matrices whose entries are respectivelyreal numbersorcomplex numbers.More general types of entries are discussedbelow.For instance, this is a real matrix:

$\mathbf {A} ={\begin{bmatrix}-1.3&0.6\\20.4&5.5\\9.7&-6.2\end{bmatrix}}.$

The numbers, symbols, or expressions in the matrix are called itsentriesor itselements.The horizontal and vertical lines of entries in a matrix are calledrowsandcolumns,respectively.

Size

The size of a matrix is defined by the number of rows and columns it contains. There is no limit to the number of rows and columns, that a matrix (in the usual sense) can have as long as they are positive integers. A matrix with${m}$rows and${n}$columns is called an${m\times n}$matrix, or${m}$-by-${n}$matrix, where${m}$and${n}$are called itsdimensions.For example, the matrix${\mathbf {A} }$above is a${3\times 2}$matrix.

Matrices with a single row are calledrow vectors,and those with a single column are calledcolumn vectors.A matrix with the same number of rows and columns is called asquare matrix.A matrix with an infinite number of rows or columns (or both) is called aninfinite matrix.In some contexts, such ascomputer algebra programs,it is useful to consider a matrix with no rows or no columns, called anempty matrix.

Overview of a matrix size

Name	Size	Example	Description	Notation
Row vector	1×n	${\begin{bmatrix}3&7&2\end{bmatrix}}$	A matrix with one row, sometimes used to represent a vector	${a_{i}}$
Column vector	n×1	${\begin{bmatrix}4\\1\\8\end{bmatrix}}$	A matrix with one column, sometimes used to represent a vector	${a_{j}}$
Square matrix	n×n	${\begin{bmatrix}9&13&5\\1&11&7\\2&6&3\end{bmatrix}}$	A matrix with the same number of rows and columns, sometimes used to represent alinear transformationfrom a vector space to itself, such asreflection,rotation,orshearing.	${\mathbf {A} }$

Notation

The specifics of symbolic matrix notation vary widely, with some prevailing trends. Matrices are commonly written insquare bracketsorparentheses,so that an$m\times n$matrix$\mathbf {A}$is represented as $$\mathbf {A} ={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{bmatrix}}={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{pmatrix}}.$$ This may be abbreviated by writing only a single generic term, possibly along with indices, as in $$\mathbf {A} =\left(a_{ij}\right),\quad \left[a_{ij}\right],\quad {\text{or}}\quad \left(a_{ij}\right)_{1\leq i\leq m,\;1\leq j\leq n}$$ or$\mathbf {A} =(a_{i,j})_{1\leq i,j\leq n}$in the case that$n=m$.

Matrices are usually symbolized usingupper-caseletters (such as${\mathbf {A} }$in the examples above), while the correspondinglower-caseletters, with two subscript indices (e.g.,${a_{11}}$,or${a_{1,1}}$), represent the entries. In addition to using upper-case letters to symbolize matrices, many authors use a specialtypographical style,commonly boldface Roman (non-italic), to further distinguish matrices from other mathematical objects. An alternative notation involves the use of a double-underline with the variable name, with or without boldface style, as in${\underline {\underline {A}}}$.

The entry in thei-th row andj-th column of a matrixAis sometimes referred to as the${i,j}$or${(i,j)}$entry of the matrix, and commonly denoted by${a_{i,j}}$or${a_{ij}}$.Alternative notations for that entry are${\mathbf {A} [i,j]}$and${\mathbf {A} _{i,j}}$.For example, the$(1,3)$entry of the following matrix$\mathbf {A}$is5(also denoted${a_{13}}$,${a_{1,3}}$,$\mathbf {A} [1,3]$or${{\mathbf {A} }_{1,3}}$):

$\mathbf {A} ={\begin{bmatrix}4&-7&\color {red}{5}&0\\-2&0&11&8\\19&1&-3&12\end{bmatrix}}$

Sometimes, the entries of a matrix can be defined by a formula such as$a_{i,j}=f(i,j)$.For example, each of the entries of the following matrix$\mathbf {A}$is determined by the formula$a_{ij}=i-j$.

$\mathbf {A} ={\begin{bmatrix}0&-1&-2&-3\\1&0&-1&-2\\2&1&0&-1\end{bmatrix}}$

In this case, the matrix itself is sometimes defined by that formula, within square brackets or double parentheses. For example, the matrix above is defined as${\mathbf {A} }=[i-j]$or${\mathbf {A} }=((i-j))$.If matrix size is$m\times n$,the above-mentioned formula$f(i,j)$is valid for any$i=1,\dots,m$and any$j=1,\dots,n$.This can be specified separately or indicated using$m\times n$as a subscript. For instance, the matrix$\mathbf {A}$above is$3\times 4$,and can be defined as${\mathbf {A} }=[i-j](i=1,2,3;j=1,\dots,4)$or${\mathbf {A} }=[i-j]_{3\times 4}$.

Some programming languages utilize doubly subscripted arrays (or arrays of arrays) to represent anm-by-nmatrix. Some programming languages start the numbering of array indexes at zero, in which case the entries of anm-by-nmatrix are indexed by$0\leq i\leq m-1$and$0\leq j\leq n-1$.This article follows the more common convention in mathematical writing where enumeration starts from1.

Thesetof allm-by-nreal matrices is often denoted${\mathcal {M}}(m,n),$or${\mathcal {M}}_{m\times n}(\mathbb {R} ).$The set of allm-by-nmatrices over anotherfield,or over aringR,is similarly denoted${\mathcal {M}}(m,n,R),$or${\mathcal {M}}_{m\times n}(R).$Ifm=n,such as in the case ofsquare matrices,one does not repeat the dimension:${\mathcal {M}}(n,R),$or${\mathcal {M}}_{n}(R).$Often,$M$,or$\operatorname {Mat}$,is used in place of${\mathcal {M}}.$

Basic operations

Several basic operations can be applied to matrices. Some, such astranspositionandsubmatrixdo not depend on the nature of the entries. Others, such asmatrix addition,scalar multiplication,matrix multiplication,androw operationsinvolve operations on matrix entries and therefore require that matrix entries are numbers or belong to afieldor aring.

In this section, it is supposed that matrix entries belong to a fixed ring, which is typically a field of numbers.

Addition, scalar multiplication, subtraction and transposition

Addition

ThesumA+Bof twom×nmatricesAandBis calculated entrywise: $$({\mathbf {A}}+{\mathbf {B}})_{i,j}={\mathbf {A}}_{i,j}+{\mathbf {B}}_{i,j},\quad 1\leq i\leq m,\quad 1\leq j\leq n.$$ For example,

${\begin{bmatrix}1&3&1\\1&0&0\end{bmatrix}}+{\begin{bmatrix}0&0&5\\7&5&0\end{bmatrix}}={\begin{bmatrix}1+0&3+0&1+5\\1+7&0+5&0+0\end{bmatrix}}={\begin{bmatrix}1&3&6\\8&5&0\end{bmatrix}}$

Scalar multiplication

The productcAof a numberc(also called ascalarin this context) and a matrixAis computed by multiplying every entry ofAbyc: $$(c{\mathbf {A}})_{i,j}=c\cdot {\mathbf {A}}_{i,j}$$ This operation is calledscalar multiplication,but its result is not named "scalar product" to avoid confusion, since "scalar product" is often used as a synonym for "inner product".For example:

$2\cdot {\begin{bmatrix}1&8&-3\\4&-2&5\end{bmatrix}}={\begin{bmatrix}2\cdot 1&2\cdot 8&2\cdot -3\\2\cdot 4&2\cdot -2&2\cdot 5\end{bmatrix}}={\begin{bmatrix}2&16&-6\\8&-4&10\end{bmatrix}}$

Subtraction

The subtraction of twom×nmatrices is defined by composing matrix addition with scalar multiplication by–1:

$\mathbf {A} -\mathbf {B} =\mathbf {A} +(-1)\cdot \mathbf {B}$

Transposition

Thetransposeof anm×nmatrixAis then×mmatrixA^T(also denotedA^tror^tA) formed by turning rows into columns and vice versa: $$\left({\mathbf {A}}^{\rm {T}}\right)_{i,j}={\mathbf {A}}_{j,i}.$$ For example:

${\begin{bmatrix}1&2&3\\0&-6&7\end{bmatrix}}^{\mathrm {T} }={\begin{bmatrix}1&0\\2&-6\\3&7\end{bmatrix}}$

Familiar properties of numbers extend to these operations on matrices: for example, addition iscommutative,that is, the matrix sum does not depend on the order of the summands:A+B=B+A. The transpose is compatible with addition and scalar multiplication, as expressed by(cA)^T=c(A^T)and(A+B)^T=A^T+B^T.Finally,(A^T)^T=A.

Matrix multiplication

Main article:Matrix multiplication

Schematic depiction of the matrix productABof two matricesAandB

Multiplicationof two matrices is defined if and only if the number of columns of the left matrix is the same as the number of rows of the right matrix. IfAis anm×nmatrix andBis ann×pmatrix, then theirmatrix productABis them×pmatrix whose entries are given bydot productof the corresponding row ofAand the corresponding column ofB:

$[\mathbf {AB} ]_{i,j}=a_{i,1}b_{1,j}+a_{i,2}b_{2,j}+\cdots +a_{i,n}b_{n,j}=\sum _{r=1}^{n}a_{i,r}b_{r,j},$

where1 ≤i≤mand1 ≤j≤p.For example, the underlined entry 2340 in the product is calculated as(2 × 1000) + (3 × 100) + (4 × 10) = 2340:

${\begin{aligned}{\begin{bmatrix}{\underline {2}}&{\underline {3}}&{\underline {4}}\\1&0&0\\\end{bmatrix}}{\begin{bmatrix}0&{\underline {1000}}\\1&{\underline {100}}\\0&{\underline {10}}\\\end{bmatrix}}&={\begin{bmatrix}3&{\underline {2340}}\\0&1000\\\end{bmatrix}}.\end{aligned}}$

Matrix multiplication satisfies the rules(AB)C=A(BC)(associativity), and(A+B)C=AC+BCas well asC(A+B) =CA+CB(left and rightdistributivity), whenever the size of the matrices is such that the various products are defined.The productABmay be defined withoutBAbeing defined, namely ifAandBarem×nandn×kmatrices, respectively, andm≠k.Even if both products are defined, they generally need not be equal, that is: $${\mathbf {AB}}\neq {\mathbf {BA}}.$$

In other words,matrix multiplication is notcommutative,in marked contrast to (rational, real, or complex) numbers, whose product is independent of the order of the factors.An example of two matrices not commuting with each other is:

${\begin{bmatrix}1&2\\3&4\\\end{bmatrix}}{\begin{bmatrix}0&1\\0&0\\\end{bmatrix}}={\begin{bmatrix}0&1\\0&3\\\end{bmatrix}},$

whereas

${\begin{bmatrix}0&1\\0&0\\\end{bmatrix}}{\begin{bmatrix}1&2\\3&4\\\end{bmatrix}}={\begin{bmatrix}3&4\\0&0\\\end{bmatrix}}.$

Besides the ordinary matrix multiplication just described, other less frequently used operations on matrices that can be considered forms of multiplication also exist, such as theHadamard productand theKronecker product.They arise in solving matrix equations such as theSylvester equation.

Row operations

Main article:Row operations

There are three types of row operations:

1. row addition, that is adding a row to another.
2. row multiplication, that is multiplying all entries of a row by a non-zero constant;
3. row switching, that is interchanging two rows of a matrix;

These operations are used in several ways, including solvinglinear equationsand findingmatrix inverses.

Submatrix

Asubmatrixof a matrix is a matrix obtained by deleting any collection of rows and/or columns.For example, from the following 3-by-4 matrix, we can construct a 2-by-3 submatrix by removing row 3 and column 2:

$\mathbf {A} ={\begin{bmatrix}1&\color {red}{2}&3&4\\5&\color {red}{6}&7&8\\\color {red}{9}&\color {red}{10}&\color {red}{11}&\color {red}{12}\end{bmatrix}}\rightarrow {\begin{bmatrix}1&3&4\\5&7&8\end{bmatrix}}.$

Theminorsand cofactors of a matrix are found by computing thedeterminantof certain submatrices.

Aprincipal submatrixis a square submatrix obtained by removing certain rows and columns. The definition varies from author to author. According to some authors, a principal submatrix is a submatrix in which the set of row indices that remain is the same as the set of column indices that remain.Other authors define a principal submatrix as one in which the firstkrows and columns, for some numberk,are the ones that remain;this type of submatrix has also been called aleading principal submatrix.

Linear equations

Main articles:Linear equationandSystem of linear equations

Matrices can be used to compactly write and work with multiple linear equations, that is, systems of linear equations. For example, ifAis anm×nmatrix,xdesignates a column vector (that is,n×1-matrix) ofnvariablesx₁,x₂,...,x_n,andbis anm×1-column vector, then the matrix equation

$\mathbf {Ax} =\mathbf {b}$

is equivalent to the system of linear equations

${\begin{aligned}a_{1,1}x_{1}+a_{1,2}x_{2}+&\cdots +a_{1,n}x_{n}=b_{1}\\&\ \ \vdots \\a_{m,1}x_{1}+a_{m,2}x_{2}+&\cdots +a_{m,n}x_{n}=b_{m}\end{aligned}}$

Using matrices, this can be solved more compactly than would be possible by writing out all the equations separately. Ifn=mand the equations areindependent,then this can be done by writing

$\mathbf {x} =\mathbf {A} ^{-1}\mathbf {b}$

whereA⁻¹is theinverse matrixofA.IfAhas no inverse, solutions—if any—can be found using itsgeneralized inverse.

Linear transformations

Main articles:Linear transformationandTransformation matrix

The vectors represented by a 2-by-2 matrix correspond to the sides of a unit square transformed into a parallelogram.

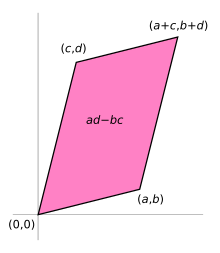
Matrices and matrix multiplication reveal their essential features when related tolinear transformations,also known aslinear maps.A realm-by-nmatrixAgives rise to a linear transformation$\mathbb {R} ^{n}\to \mathbb {R} ^{m}$mapping each vectorxin⁠$\mathbb {R} ^{n}$⁠to the (matrix) productAx,which is a vector in⁠$\mathbb {R} ^{m}.$⁠Conversely, each linear transformation$f:\mathbb {R} ^{n}\to \mathbb {R} ^{m}$arises from a uniquem-by-nmatrixA:explicitly, the(i,j)-entry ofAis theith coordinate off (e_j),wheree_j= (0,..., 0, 1, 0,..., 0)is theunit vectorwith 1 in thejth position and 0 elsewhere.The matrixAis said to represent the linear mapf,andAis called thetransformation matrixoff.

For example, the 2×2 matrix

$\mathbf {A} ={\begin{bmatrix}a&c\\b&d\end{bmatrix}}$

can be viewed as the transform of theunit squareinto aparallelogramwith vertices at(0, 0),(a,b),(a+c,b+d),and(c,d).The parallelogram pictured at the right is obtained by multiplyingAwith each of the column vectors${\begin{bmatrix}0\\0\end{bmatrix}},{\begin{bmatrix}1\\0\end{bmatrix}},{\begin{bmatrix}1\\1\end{bmatrix}}$,and${\begin{bmatrix}0\\1\end{bmatrix}}$in turn. These vectors define the vertices of the unit square.

The following table shows several 2×2 real matrices with the associated linear maps of⁠$\mathbb {R} ^{2}.$⁠Theblueoriginal is mapped to thegreengrid and shapes. The origin(0, 0)is marked with a black point.

Horizontal shear withm= 1.25.	Reflectionthrough the vertical axis	Squeeze mapping withr= 3/2	Scaling by a factor of 3/2	Rotation byπ/6 = 30°
${\begin{bmatrix}1&1.25\\0&1\end{bmatrix}}$	${\begin{bmatrix}-1&0\\0&1\end{bmatrix}}$	${\begin{bmatrix}{\frac {3}{2}}&0\\0&{\frac {2}{3}}\end{bmatrix}}$	${\begin{bmatrix}{\frac {3}{2}}&0\\0&{\frac {3}{2}}\end{bmatrix}}$	${\begin{bmatrix}\cos \left({\frac {\pi }{6}}\right)&-\sin \left({\frac {\pi }{6}}\right)\\\sin \left({\frac {\pi }{6}}\right)&\cos \left({\frac {\pi }{6}}\right)\end{bmatrix}}$

Under the1-to-1 correspondencebetween matrices and linear maps, matrix multiplication corresponds tocompositionof maps:if ak-by-mmatrixBrepresents another linear map$g:\mathbb {R} ^{m}\to \mathbb {R} ^{k}$,then the compositiong∘fis represented byBAsince $$(g\circ f)({\mathbf {x}})=g(f({\mathbf {x}}))=g({\mathbf {Ax}})={\mathbf {B}}({\mathbf {Ax}})=({\mathbf {BA}}){\mathbf {x}}.$$

The last equality follows from the above-mentioned associativity of matrix multiplication.

Therank of a matrixAis the maximum number oflinearly independentrow vectors of the matrix, which is the same as the maximum number of linearly independent column vectors.Equivalently it is thedimensionof theimageof the linear map represented byA.Therank–nullity theoremstates that the dimension of thekernelof a matrix plus the rank equals the number of columns of the matrix.

Square matrix

Main article:Square matrix

Asquare matrixis a matrix with the same number of rows and columns.Ann-by-nmatrix is known as a square matrix of ordern.Any two square matrices of the same order can be added and multiplied. The entriesa_iiform themain diagonalof a square matrix. They lie on the imaginary line that runs from the top left corner to the bottom right corner of the matrix.

Main types

Name	Example withn= 3
Diagonal matrix	${\begin{bmatrix}a_{11}&0&0\\0&a_{22}&0\\0&0&a_{33}\\\end{bmatrix}}$
Lower triangular matrix	${\begin{bmatrix}a_{11}&0&0\\a_{21}&a_{22}&0\\a_{31}&a_{32}&a_{33}\\\end{bmatrix}}$
Upper triangular matrix	${\begin{bmatrix}a_{11}&a_{12}&a_{13}\\0&a_{22}&a_{23}\\0&0&a_{33}\\\end{bmatrix}}$

Diagonal and triangular matrix

If all entries ofAbelow the main diagonal are zero,Ais called anuppertriangular matrix.Similarly, if all entries ofAabove the main diagonal are zero,Ais called alower triangular matrix.If all entries outside the main diagonal are zero,Ais called adiagonal matrix.

Identity matrix

Main article:Identity matrix

Theidentity matrixI_nof sizenis then-by-nmatrix in which all the elements on themain diagonalare equal to 1 and all other elements are equal to 0, for example, $${\begin{aligned}\mathbf {I} _{1}&={\begin{bmatrix}1\end{bmatrix}},\\[4pt]\mathbf {I} _{2}&={\begin{bmatrix}1&0\\0&1\end{bmatrix}},\\[4pt]\vdots &\\[4pt]\mathbf {I} _{n}&={\begin{bmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{bmatrix}}\end{aligned}}$$ It is a square matrix of ordern,and also a special kind ofdiagonal matrix.It is called an identity matrix because multiplication with it leaves a matrix unchanged: $${\mathbf {AI}}_{n}={\mathbf {I}}_{m}{\mathbf {A}}={\mathbf {A}}$$ for anym-by-nmatrixA.

A nonzero scalar multiple of an identity matrix is called ascalarmatrix. If the matrix entries come from a field, the scalar matrices form a group, under matrix multiplication, that is isomorphic to the multiplicative group of nonzero elements of the field.

Symmetric or skew-symmetric matrix

A square matrixAthat is equal to its transpose, that is,A=A^T,is asymmetric matrix.If instead,Ais equal to the negative of its transpose, that is,A= −A^T,thenAis askew-symmetric matrix.In complex matrices, symmetry is often replaced by the concept ofHermitian matrices,which satisfiesA^∗=A,where the star orasteriskdenotes theconjugate transposeof the matrix, that is, the transpose of thecomplex conjugateofA.

By thespectral theorem,real symmetric matrices and complex Hermitian matrices have aneigenbasis;that is, every vector is expressible as alinear combinationof eigenvectors. In both cases, all eigenvalues are real.This theorem can be generalized to infinite-dimensional situations related to matrices with infinitely many rows and columns, seebelow.

Invertible matrix and its inverse

A square matrixAis calledinvertibleornon-singularif there exists a matrixBsuch that $${\mathbf {AB}}={\mathbf {BA}}={\mathbf {I}}_{n},$$ whereI_nis then×nidentity matrixwith 1s on themain diagonaland 0s elsewhere. IfBexists, it is unique and is called theinverse matrixofA,denotedA⁻¹.

Definite matrix

Positive definite matrix	Indefinite matrix
${\begin{bmatrix}{\frac {1}{4}}&0\\0&1\\\end{bmatrix}}$	${\begin{bmatrix}{\frac {1}{4}}&0\\0&-{\frac {1}{4}}\end{bmatrix}}$
$Q(x,y)={\frac {1}{4}}x^{2}+y^{2}$	$Q(x,y)={\frac {1}{4}}x^{2}-{\frac {1}{4}}y^{2}$
Points such that${\textstyle Q(x,y)=1}$ (Ellipse)	Points such that${\textstyle Q(x,y)=1}$ (Hyperbola)

A symmetric real matrixAis calledpositive-definiteif the associatedquadratic form $$f({\mathbf {x}})={\mathbf {x}}^{\rm {T}}{\mathbf {Ax}}$$ has a positive value for every nonzero vectorxin⁠$\mathbb {R} ^{n}.$⁠Iff (x)only yields negative values thenAisnegative-definite;iffdoes produce both negative and positive values thenAisindefinite.If the quadratic formfyields only non-negative values (positive or zero), the symmetric matrix is calledpositive-semidefinite(or if only non-positive values, then negative-semidefinite); hence the matrix is indefinite precisely when it is neither positive-semidefinite nor negative-semidefinite.

A symmetric matrix is positive-definite if and only if all its eigenvalues are positive, that is, the matrix is positive-semidefinite and it is invertible.The table at the right shows two possibilities for 2-by-2 matrices.

Allowing as input two different vectors instead yields thebilinear formassociated toA: $$B_{\mathbf {A}}({\mathbf {x}},{\mathbf {y}})={\mathbf {x}}^{\rm {T}}{\mathbf {Ay}}.$$

In the case of complex matrices, the same terminology and result apply, withsymmetric matrix,quadratic form,bilinear form,andtransposex^Treplaced respectively byHermitian matrix,Hermitian form,sesquilinear form,andconjugate transposex^H.

Orthogonal matrix

Main article:Orthogonal matrix

Anorthogonal matrixis a square matrix withrealentries whose columns and rows areorthogonalunit vectors(that is,orthonormalvectors). Equivalently, a matrixAis orthogonal if itstransposeis equal to itsinverse:

$\mathbf {A} ^{\mathrm {T} }=\mathbf {A} ^{-1},\,$

which entails

$\mathbf {A} ^{\mathrm {T} }\mathbf {A} =\mathbf {A} \mathbf {A} ^{\mathrm {T} }=\mathbf {I} _{n},$

whereI_nis theidentity matrixof sizen.

An orthogonal matrixAis necessarilyinvertible(with inverseA⁻¹=A^T),unitary(A⁻¹=A*), andnormal(A*A=AA*). Thedeterminantof any orthogonal matrix is either+1or−1.Aspecial orthogonal matrixis an orthogonal matrix withdeterminant+1. As alinear transformation,every orthogonal matrix with determinant+1is a purerotationwithout reflection, i.e., the transformation preserves the orientation of the transformed structure, while every orthogonal matrix with determinant-1reverses the orientation, i.e., is a composition of a purereflectionand a (possibly null) rotation. The identity matrices have determinant1and are pure rotations by an angle zero.

Thecomplexanalog of an orthogonal matrix is aunitary matrix.

Main operations

Trace

Thetrace,tr(A)of a square matrixAis the sum of its diagonal entries. While matrix multiplication is not commutative as mentionedabove,the trace of the product of two matrices is independent of the order of the factors:

$\operatorname {tr} (\mathbf {AB} )=\operatorname {tr} (\mathbf {BA} ).$

This is immediate from the definition of matrix multiplication:

$\operatorname {tr} (\mathbf {AB} )=\sum _{i=1}^{m}\sum _{j=1}^{n}a_{ij}b_{ji}=\operatorname {tr} (\mathbf {BA} ).$

It follows that the trace of the product of more than two matrices is independent ofcyclic permutationsof the matrices, however, this does not in general apply for arbitrary permutations (for example,tr(ABC) ≠ tr(BAC),in general). Also, the trace of a matrix is equal to that of its transpose, that is, $$\operatorname {tr} ({\mathbf {A}})=\operatorname {tr} ({\mathbf {A}}^{\rm {T}}).$$

Determinant

Main article:Determinant

A linear transformation on⁠$\mathbb {R} ^{2}$⁠given by the indicated matrix. The determinant of this matrix is −1, as the area of the green parallelogram at the right is 1, but the map reverses theorientation,since it turns the counterclockwise orientation of the vectors to a clockwise one.

Thedeterminantof a square matrixA(denoteddet(A)or|A|) is a number encoding certain properties of the matrix. A matrix is invertibleif and only ifits determinant is nonzero. Itsabsolute valueequals the area (in⁠$\mathbb {R} ^{2}$⁠) or volume (in⁠$\mathbb {R} ^{3}$⁠) of the image of the unit square (or cube), while its sign corresponds to the orientation of the corresponding linear map: the determinant is positive if and only if the orientation is preserved.

The determinant of 2-by-2 matrices is given by

$\det {\begin{bmatrix}a&b\\c&d\end{bmatrix}}=ad-bc.$

The determinant of 3-by-3 matrices involves 6 terms (rule of Sarrus). The more lengthyLeibniz formulageneralizes these two formulae to all dimensions.

The determinant of a product of square matrices equals the product of their determinants: $$\det({\mathbf {AB}})=\det({\mathbf {A}})\cdot \det({\mathbf {B}}),$$ or using alternate notation: $$|{\mathbf {AB}}|=|{\mathbf {A}}|\cdot |{\mathbf {B}}|.$$ Adding a multiple of any row to another row, or a multiple of any column to another column does not change the determinant. Interchanging two rows or two columns affects the determinant by multiplying it by −1.Using these operations, any matrix can be transformed to a lower (or upper) triangular matrix, and for such matrices, the determinant equals the product of the entries on the main diagonal; this provides a method to calculate the determinant of any matrix. Finally, theLaplace expansionexpresses the determinant in terms ofminors,that is, determinants of smaller matrices.This expansion can be used for a recursive definition of determinants (taking as starting case the determinant of a 1-by-1 matrix, which is its unique entry, or even the determinant of a 0-by-0 matrix, which is 1), that can be seen to be equivalent to the Leibniz formula. Determinants can be used to solvelinear systemsusingCramer's rule,where the division of the determinants of two related square matrices equates to the value of each of the system's variables.

Eigenvalues and eigenvectors

Main article:Eigenvalues and eigenvectors

A number${\textstyle \lambda }$and a non-zero vectorvsatisfying

$\mathbf {A} \mathbf {v} =\lambda \mathbf {v}$

are called aneigenvalueand aneigenvectorofA,respectively.The numberλis an eigenvalue of ann×n-matrixAif and only if(A− λI_n)is not invertible, which isequivalentto

$\det(\mathbf {A} -\lambda \mathbf {I} )=0.$

The polynomialp_Ain anindeterminateXgiven by evaluation of the determinantdet(X I_n−A)is called thecharacteristic polynomialofA.It is amonic polynomialofdegreen.Therefore the polynomial equationp_A(λ) = 0has at mostndifferent solutions, that is, eigenvalues of the matrix.They may be complex even if the entries ofAare real. According to theCayley–Hamilton theorem,p_A(A) =0,that is, the result of substituting the matrix itself into its characteristic polynomial yields thezero matrix.

Computational aspects

Matrix calculations can be often performed with different techniques. Many problems can be solved by both direct algorithms and iterative approaches. For example, the eigenvectors of a square matrix can be obtained by finding asequenceof vectorsx_nconvergingto an eigenvector whenntends toinfinity.

To choose the most appropriate algorithm for each specific problem, it is important to determine both the effectiveness and precision of all the available algorithms. The domain studying these matters is callednumerical linear algebra.As with other numerical situations, two main aspects are thecomplexityof algorithms and theirnumerical stability.

Determining the complexity of an algorithm means findingupper boundsor estimates of how many elementary operations such as additions and multiplications of scalars are necessary to perform some algorithm, for example,multiplication of matrices.Calculating the matrix product of twon-by-nmatrices using the definition given above needsn³multiplications, since for any of then²entries of the product,nmultiplications are necessary. TheStrassen algorithmoutperforms this "naive" algorithm; it needs onlyn^2.807multiplications.A refined approach also incorporates specific features of the computing devices.

In many practical situations, additional information about the matrices involved is known. An important case issparse matrices,that is, matrices most of whose entries are zero. There are specifically adapted algorithms for, say, solving linear systemsAx=bfor sparse matricesA,such as theconjugate gradient method.

An algorithm is, roughly speaking, numerically stable if little deviations in the input values do not lead to big deviations in the result. For example, calculating the inverse of a matrix via Laplace expansion (adj(A)denotes theadjugate matrixofA) $${\mathbf {A}}^{-1}=\operatorname {adj} ({\mathbf {A}})/\det({\mathbf {A}})$$ may lead to significant rounding errors if the determinant of the matrix is very small. Thenorm of a matrixcan be used to capture theconditioningof linear algebraic problems, such as computing a matrix's inverse.

Most computerprogramming languagessupport arrays but are not designed with built-in commands for matrices. Instead, available external libraries provide matrix operations on arrays, in nearly all currently used programming languages. Matrix manipulation was among the earliest numerical applications of computers.The originalDartmouth BASIChad built-in commands for matrix arithmetic on arrays from itssecond editionimplementation in 1964. As early as the 1970s, some engineering desktop computers such as theHP 9830hadROM cartridges to add BASIC commands for matrices.Some computer languages such asAPLwere designed to manipulate matrices, andvarious mathematical programscan be used to aid computing with matrices.As of 2023, most computers have some form of built-in matrix operations at a low level implementing the standardBLASspecification, upon which most higher-level matrix and linear algebra libraries (e.g.,EISPACK,LINPACK,LAPACK) rely. While most of these libraries require a professional level of coding,LAPACKcan be accessed by higher-level (and user-friendly) bindings such asNumPy/SciPy,R,GNU Octave,MATLAB.

Decomposition

Main articles:Matrix decomposition,Matrix diagonalization,Gaussian elimination,andBareiss algorithm

There are several methods to render matrices into a more easily accessible form. They are generally referred to asmatrix decompositionormatrix factorizationtechniques. The interest of all these techniques is that they preserve certain properties of the matrices in question, such as determinant, rank, or inverse, so that these quantities can be calculated after applying the transformation, or that certain matrix operations are algorithmically easier to carry out for some types of matrices.

TheLU decompositionfactors matrices as a product of lower (L) and an uppertriangular matrices(U).Once this decomposition is calculated, linear systems can be solved more efficiently, by a simple technique calledforward and back substitution.Likewise, inverses of triangular matrices are algorithmically easier to calculate. TheGaussian eliminationis a similar algorithm; it transforms any matrix torow echelon form.Both methods proceed by multiplying the matrix by suitableelementary matrices,which correspond topermuting rows or columnsand adding multiples of one row to another row.Singular value decompositionexpresses any matrixAas a productUDV^∗,whereUandVareunitary matricesandDis a diagonal matrix.

An example of a matrix in Jordan normal form. The grey blocks are called Jordan blocks.

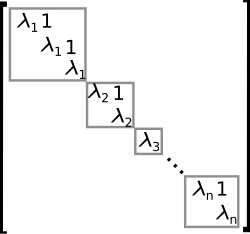
TheeigendecompositionordiagonalizationexpressesAas a productVDV⁻¹,whereDis a diagonal matrix andVis a suitable invertible matrix.IfAcan be written in this form, it is calleddiagonalizable.More generally, and applicable to all matrices, the Jordan decomposition transforms a matrix intoJordan normal form,that is to say matrices whose only nonzero entries are the eigenvaluesλ₁toλ_nofA,placed on the main diagonal and possibly entries equal to one directly above the main diagonal, as shown at the right.Given the eigendecomposition, thenth power ofA(that is,n-fold iterated matrix multiplication) can be calculated via $${\mathbf {A}}^{n}=({\mathbf {VDV}}^{-1})^{n}={\mathbf {VDV}}^{-1}{\mathbf {VDV}}^{-1}\ldots {\mathbf {VDV}}^{-1}={\mathbf {VD}}^{n}{\mathbf {V}}^{-1}$$ and the power of a diagonal matrix can be calculated by taking the corresponding powers of the diagonal entries, which is much easier than doing the exponentiation forAinstead. This can be used to compute thematrix exponentiale^A,a need frequently arising in solvinglinear differential equations,matrix logarithmsandsquare roots of matrices.To avoid numericallyill-conditionedsituations, further algorithms such as theSchur decompositioncan be employed.

Abstract algebraic aspects and generalizations

Matrices can be generalized in different ways. Abstract algebra uses matrices with entries in more generalfieldsor evenrings,while linear algebra codifies properties of matrices in the notion of linear maps. It is possible to consider matrices with infinitely many columns and rows. Another extension istensors,which can be seen as higher-dimensional arrays of numbers, as opposed to vectors, which can often be realized as sequences of numbers, while matrices are rectangular or two-dimensional arrays of numbers.Matrices, subject to certain requirements tend to formgroupsknown as matrix groups. Similarly under certain conditions matrices formringsknown asmatrix rings.Though the product of matrices is not in general commutative certain matrices formfieldsknown asmatrix fields. In general, matrices and theirmultiplicationalso form acategory,thecategory of matrices.

Matrices with more general entries

This article focuses on matrices whose entries are real or complex numbers.However, matrices can be considered with much more general types of entries than real or complex numbers.As a first step of generalization, anyfield,that is, asetwhereaddition,subtraction,multiplication,anddivisionoperations are defined and well-behaved, may be used instead of⁠$\mathbb {R}$⁠or⁠$\mathbb {C},$⁠for examplerational numbersorfinite fields.For example,coding theorymakes use of matrices over finite fields. Wherevereigenvaluesare considered, as these are roots of a polynomial they may exist only in a larger field than that of the entries of the matrix; for instance, they may be complex in the case of a matrix with real entries. The possibility to reinterpret the entries of a matrix as elements of a larger field (for example, to view a real matrix as a complex matrix whose entries happen to be all real) then allows considering each square matrix to possess a full set of eigenvalues. Alternatively one can consider only matrices with entries in analgebraically closed field,such as⁠$\mathbb {C},$⁠from the outset.

More generally, matrices with entries in aringRare widely used in mathematics.Rings are a more general notion than fields in that a division operation need not exist. The very same addition and multiplication operations of matrices extend to this setting, too. The setM(n,R)(also denotedM_n(R)) of all squaren-by-nmatrices overRis a ring calledmatrix ring,isomorphic to theendomorphism ringof the leftR-moduleRⁿ.If the ringRiscommutative,that is, its multiplication is commutative, then the ringM(n,R)is also anassociative algebraoverR.Thedeterminantof square matrices over a commutative ringRcan still be defined using theLeibniz formula;such a matrix is invertible if and only if its determinant isinvertibleinR,generalizing the situation over a fieldF,where every nonzero element is invertible.Matrices oversuperringsare calledsupermatrices.

Matrices do not always have all their entries in the same ring– or even in any ring at all. One special but common case isblock matrices,which may be considered as matrices whose entries themselves are matrices. The entries need not be square matrices, and thus need not be members of anyring;but their sizes must fulfill certain compatibility conditions.

Relationship to linear maps

Linear maps$\mathbb {R} ^{n}\to \mathbb {R} ^{m}$are equivalent tom-by-nmatrices, as describedabove.More generally, any linear mapf :V→Wbetween finite-dimensionalvector spacescan be described by a matrixA= (a_ij),after choosingbasesv₁,...,v_nofV,andw₁,...,w_mofW(sonis the dimension ofVandmis the dimension ofW), which is such that

$f(\mathbf {v} _{j})=\sum _{i=1}^{m}a_{i,j}\mathbf {w} _{i}\qquad {\mbox{for}}\ j=1,\ldots,n.$

In other words, columnjofAexpresses the image ofv_jin terms of the basis vectorsw_IofW;thus this relation uniquely determines the entries of the matrixA.The matrix depends on the choice of the bases: different choices of bases give rise to different, butequivalent matrices.Many of the above concrete notions can be reinterpreted in this light, for example, the transpose matrixA^Tdescribes thetranspose of the linear mapgiven byA,concerning thedual bases.

These properties can be restated more naturally: thecategory of matriceswith entries in a field$k$with multiplication as composition isequivalentto the category of finite-dimensionalvector spacesand linear maps over this field.

More generally, the set ofm×nmatrices can be used to represent theR-linear maps between the free modulesR^mandRⁿfor an arbitrary ringRwith unity. Whenn=mcomposition of these maps is possible, and this gives rise to thematrix ringofn×nmatrices representing theendomorphism ringofRⁿ.

Matrix groups

Main article:Matrix group

Agroupis a mathematical structure consisting of a set of objects together with abinary operation,that is, an operation combining any two objects to a third, subject to certain requirements.A group in which the objects are matrices and the group operation is matrix multiplication is called amatrix group.Since a group of every element must be invertible, the most general matrix groups are the groups of all invertible matrices of a given size, called thegeneral linear groups.

Any property of matrices that is preserved under matrix products and inverses can be used to define further matrix groups. For example, matrices with a given size and with a determinant of 1 form asubgroupof (that is, a smaller group contained in) their general linear group, called aspecial linear group.Orthogonal matrices,determined by the condition $${\mathbf {M}}^{\rm {T}}{\mathbf {M}}={\mathbf {I}},$$ form theorthogonal group.Every orthogonal matrix hasdeterminant1 or −1. Orthogonal matrices with determinant 1 form a subgroup calledspecial orthogonal group.

Everyfinite groupisisomorphicto a matrix group, as one can see by considering theregular representationof thesymmetric group.General groups can be studied using matrix groups, which are comparatively well understood, usingrepresentation theory.

Infinite matrices

It is also possible to consider matrices with infinitely many rows and/or columnseven though, being infinite objects, one cannot write down such matrices explicitly. All that matters is that for every element in the set indexing rows, and every element in the set indexing columns, there is a well-defined entry (these index sets need not even be subsets of the natural numbers). The basic operations of addition, subtraction, scalar multiplication, and transposition can still be defined without problem; however, matrix multiplication may involve infinite summations to define the resulting entries, and these are not defined in general.

IfRis any ring with unity, then the ring of endomorphisms of$M=\bigoplus _{i\in I}R$as a rightRmodule is isomorphic to the ring ofcolumn finite matrices$\mathrm {CFM} _{I}(R)$whose entries are indexed by$I\times I$,and whose columns each contain only finitely many nonzero entries. The endomorphisms ofMconsidered as a leftRmodule result in an analogous object, therow finite matrices$\mathrm {RFM} _{I}(R)$whose rows each only have finitely many nonzero entries.

If infinite matrices are used to describe linear maps, then only those matrices can be used all of whose columns have but a finite number of nonzero entries, for the following reason. For a matrixAto describe a linear mapf :V→W,bases for both spaces must have been chosen; recall that by definition this means that every vector in the space can be written uniquely as a (finite) linear combination of basis vectors, so that written as a (column) vectorveofcoefficients,only finitely many entriesv_Iare nonzero. Now the columns ofAdescribe the images byfof individual basis vectors ofVin the basis ofW,which is only meaningful if these columns have only finitely many nonzero entries. There is no restriction on the rows ofAhowever: in the productA·vthere are only finitely many nonzero coefficients ofvinvolved, so every one of its entries, even if it is given as an infinite sum of products, involves only finitely many nonzero terms and is therefore well defined. Moreover, this amounts to forming a linear combination of the columns ofAthat effectively involves only finitely many of them, whence the result has only finitely many nonzero entries because each of those columns does. Products of two matrices of the given type are well defined (provided that the column-index and row-index sets match), are of the same type, and correspond to the composition of linear maps.

IfRis anormedring, then the condition of row or column finiteness can be relaxed. With the norm in place,absolutely convergent seriescan be used instead of finite sums. For example, the matrices whose column sums are convergent sequences form a ring. Analogously, the matrices whose row sums are convergent series also form a ring.

Infinite matrices can also be used to describeoperators on Hilbert spaces,where convergence andcontinuityquestions arise, which again results in certain constraints that must be imposed. However, the explicit point of view of matrices tends to obfuscate the matter,and the abstract and more powerful tools offunctional analysiscan be used instead.

Empty matrix

Anempty matrixis a matrix in which the number of rows or columns (or both) is zero.Empty matrices help to deal with maps involving thezero vector space.For example, ifAis a 3-by-0 matrix andBis a 0-by-3 matrix, thenABis the 3-by-3 zero matrix corresponding to the null map from a 3-dimensional spaceVto itself, whileBAis a 0-by-0 matrix. There is no common notation for empty matrices, but mostcomputer algebra systemsallow creating and computing with them. The determinant of the 0-by-0 matrix is 1 as follows regarding theempty productoccurring in the Leibniz formula for the determinant as 1. This value is also consistent with the fact that the identity map from any finite-dimensional space to itself has determinant1, a fact that is often used as a part of the characterization of determinants.

Applications

There are numerous applications of matrices, both in mathematics and other sciences. Some of them merely take advantage of the compact representation of a set of numbers in a matrix. For example, ingame theoryandeconomics,thepayoff matrixencodes the payoff for two players, depending on which out of a given (finite) set of strategies the players choose.Text miningand automatedthesauruscompilation makes use ofdocument-term matricessuch astf-idfto track frequencies of certain words in several documents.

Complex numbers can be represented by particular real 2-by-2 matrices via

$a+ib\leftrightarrow {\begin{bmatrix}a&-b\\b&a\end{bmatrix}},$

under which addition and multiplication of complex numbers and matrices correspond to each other. For example, 2-by-2 rotation matrices represent the multiplication with some complex number ofabsolute value1, asabove.A similar interpretation is possible forquaternionsandClifford algebrasin general.

Earlyencryptiontechniques such as theHill cipheralso used matrices. However, due to the linear nature of matrices, these codes are comparatively easy to break.Computer graphicsuses matrices to represent objects; to calculate transformations of objects using affinerotation matricesto accomplish tasks such as projecting a three-dimensional object onto a two-dimensional screen, corresponding to a theoretical camera observation; and to apply image convolutions such as sharpening, blurring, edge detection, and more.Matrices over apolynomial ringare important in the study ofcontrol theory.

Chemistrymakes use of matrices in various ways, particularly since the use ofquantum theoryto discussmolecular bondingandspectroscopy.Examples are theoverlap matrixand theFock matrixused in solving theRoothaan equationsto obtain themolecular orbitalsof theHartree–Fock method.

Graph theory

An undirected graph with adjacency matrix:$${\begin{bmatrix}1&1&0\\1&0&1\\0&1&0\end{bmatrix}}.$$

Theadjacency matrixof afinite graphis a basic notion ofgraph theory.It records which vertices of the graph are connected by an edge. Matrices containing just two different values (1 and 0 meaning for example "yes" and "no", respectively) are calledlogical matrices.Thedistance (or cost) matrixcontains information about the distances of the edges.These concepts can be applied towebsitesconnected byhyperlinksor cities connected by roads etc., in which case (unless the connection network is extremely dense) the matrices tend to besparse,that is, contain few nonzero entries. Therefore, specifically tailored matrix algorithms can be used innetwork theory.

Analysis and geometry

TheHessian matrixof adifferentiable function$f:\mathbb {R} ^{n}\to \mathbb {R}$consists of thesecond derivativesofƒconcerning the several coordinate directions, that is,

$H(f)=\left[{\frac {\partial ^{2}f}{\partial x_{i}\,\partial x_{j}}}\right].$

At thesaddle point(x= 0,y= 0)(red) of the functionf (x,−y) =x²−y²,the Hessian matrix${\begin{bmatrix}2&0\\0&-2\end{bmatrix}}$isindefinite.

It encodes information about the local growth behavior of the function: given acritical pointx= (x₁,...,x_n),that is, a point where the firstpartial derivatives$\partial f/\partial x_{i}$ofƒvanish, the function has alocal minimumif the Hessian matrix ispositive definite.Quadratic programmingcan be used to find global minima or maxima of quadratic functions closely related to the ones attached to matrices (seeabove).

Another matrix frequently used in geometrical situations is theJacobi matrixof a differentiable map$f:\mathbb {R} ^{n}\to \mathbb {R} ^{m}.$Iff₁,...,f_mdenote the components off,then the Jacobi matrix is defined as

$J(f)=\left[{\frac {\partial f_{i}}{\partial x_{j}}}\right]_{1\leq i\leq m,1\leq j\leq n}.$

Ifn>m,and if the rank of the Jacobi matrix attains its maximal valuem,fis locally invertible at that point, by theimplicit function theorem.

Partial differential equationscan be classified by considering the matrix of coefficients of the highest-order differential operators of the equation. Forelliptic partial differential equationsthis matrix is positive definite, which has a decisive influence on the set of possible solutions of the equation in question.

Thefinite element methodis an important numerical method to solve partial differential equations, widely applied in simulating complex physical systems. It attempts to approximate the solution to some equation by piecewise linear functions, where the pieces are chosen concerning a sufficiently fine grid, which in turn can be recast as a matrix equation.

Probability theory and statistics

Two different Markov chains. The chart depicts the number of particles (of a total of 1000) in state "2". Both limiting values can be determined from the transition matrices, which are given by${\begin{bmatrix}0.7&0\\0.3&1\end{bmatrix}}$(red) and${\begin{bmatrix}0.7&0.2\\0.3&0.8\end{bmatrix}}$(black).

Stochastic matricesare square matrices whose rows areprobability vectors,that is, whose entries are non-negative and sum up to one. Stochastic matrices are used to defineMarkov chainswith finitely many states.A row of the stochastic matrix gives the probability distribution for the next position of some particle currently in the state that corresponds to the row. Properties of the Markov chain-likeabsorbing states,that is, states that any particle attains eventually, can be read off the eigenvectors of the transition matrices.

Statistics also makes use of matrices in many different forms.Descriptive statisticsis concerned with describing data sets, which can often be represented asdata matrices,which may then be subjected todimensionality reductiontechniques. Thecovariance matrixencodes the mutualvarianceof severalrandom variables.Another technique using matrices arelinear least squares,a method that approximates a finite set of pairs(x₁,y₁), (x₂,y₂),..., (x_N,y_N),by a linear function $$y_{i}\approx ax_{i}+b,\quad i=1,\ldots,N$$

which can be formulated in terms of matrices, related to thesingular value decompositionof matrices.

Random matricesare matrices whose entries are random numbers, subject to suitableprobability distributions,such asmatrix normal distribution.Beyond probability theory, they are applied in domains ranging fromnumber theorytophysics.

Symmetries and transformations in physics

Further information:Symmetry in physics

Linear transformations and the associatedsymmetriesplay a key role in modern physics. For example,elementary particlesinquantum field theoryare classified as representations of theLorentz groupof special relativity and, more specifically, by their behavior under thespin group.Concrete representations involving thePauli matricesand more generalgamma matricesare an integral part of the physical description offermions,which behave asspinors.For the three lightestquarks,there is a group-theoretical representation involving thespecial unitary groupSU(3); for their calculations, physicists use a convenient matrix representation known as theGell-Mann matrices,which are also used for the SU(3)gauge groupthat forms the basis of the modern description of strong nuclear interactions,quantum chromodynamics.TheCabibbo–Kobayashi–Maskawa matrix,in turn, expresses the fact that the basic quark states that are important forweak interactionsare not the same as, but linearly related to the basic quark states that define particles with specific and distinctmasses.

Linear combinations of quantum states

The first model ofquantum mechanics(Heisenberg,1925) represented the theory's operators by infinite-dimensional matrices acting on quantum states.This is also referred to asmatrix mechanics.One particular example is thedensity matrixthat characterizes the "mixed" state of a quantum system as a linear combination of elementary, "pure"eigenstates.

Another matrix serves as a key tool for describing the scattering experiments that form the cornerstone of experimental particle physics: Collision reactions such as occur inparticle accelerators,where non-interacting particles head towards each other and collide in a small interaction zone, with a new set of non-interacting particles as the result, can be described as the scalar product of outgoing particle states and a linear combination of ingoing particle states. The linear combination is given by a matrix known as theS-matrix,which encodes all information about the possible interactions between particles.

Normal modes

A general application of matrices in physics is the description of linearly coupled harmonic systems. Theequations of motionof such systems can be described in matrix form, with a mass matrix multiplying a generalized velocity to give the kinetic term, and aforcematrix multiplying a displacement vector to characterize the interactions. The best way to obtain solutions is to determine the system'seigenvectors,itsnormal modes,by diagonalizing the matrix equation. Techniques like this are crucial when it comes to the internal dynamics ofmolecules:the internal vibrations of systems consisting of mutually bound component atoms.They are also needed for describing mechanical vibrations, and oscillations in electrical circuits.

Geometrical optics

Geometrical opticsprovides further matrix applications. In this approximative theory, thewave natureof light is neglected. The result is a model in whichlight raysare indeedgeometrical rays.If the deflection of light rays by optical elements is small, the action of alensor reflective element on a given light ray can be expressed as multiplication of a two-component vector with a two-by-two matrix calledray transfer matrix analysis:the vector's components are the light ray's slope and its distance from the optical axis, while the matrix encodes the properties of the optical element. There are two kinds of matrices, viz. arefraction matrixdescribing the refraction at a lens surface, and atranslation matrix,describing the translation of the plane of reference to the next refracting surface, where another refraction matrix applies. The optical system, consisting of a combination of lenses and/or reflective elements, is simply described by the matrix resulting from the product of the components' matrices.

Electronics

Traditionalmesh analysisandnodal analysisin electronics lead to a system of linear equations that can be described with a matrix.

The behavior of manyelectronic componentscan be described using matrices. LetAbe a 2-dimensional vector with the component's input voltagev₁and input currentI₁as its elements, and letBbe a 2-dimensional vector with the component's output voltagev₂and output currentI₂as its elements. Then the behavior of the electronic component can be described byB=H·A,whereHis a 2 x 2 matrix containing oneimpedanceelement (h₁₂), oneadmittanceelement (h₂₁), and twodimensionlesselements (h₁₁andh₂₂). Calculating a circuit now reduces to multiplying matrices.

History

Matrices have a long history of application in solvinglinear equationsbut they were known as arrays until the 1800s. TheChinese textThe Nine Chapters on the Mathematical Artwritten in the 10th–2nd century BCE is the first example of the use of array methods to solvesimultaneous equations,including the concept ofdeterminants.In 1545 Italian mathematicianGerolamo Cardanointroduced the method to Europe when he publishedArs Magna.TheJapanese mathematicianSekiused the same array methods to solve simultaneous equations in 1683.The Dutch mathematicianJan de Wittrepresented transformations using arrays in his 1659 bookElements of Curves(1659).Between 1700 and 1710Gottfried Wilhelm Leibnizpublicized the use of arrays for recording information or solutions and experimented with over 50 different systems of arrays.Cramerpresentedhis rulein 1750.

The term "matrix" (Latin for "womb", "dam" (non-human female animal kept for breeding), "source", "origin", "list", and "register", are derived frommater—mother) was coined byJames Joseph Sylvesterin 1850,who understood a matrix as an object giving rise to several determinants today calledminors,that is to say, determinants of smaller matrices that derive from the original one by removing columns and rows. In an 1851 paper, Sylvester explains:

I have in previous papers defined a "Matrix" as a rectangular array of terms, out of which different systems of determinants may be engendered from the womb of a common parent.

Arthur Cayleypublished a treatise on geometric transformations using matrices that were not rotated versions of the coefficients being investigated as had previously been done. Instead, he defined operations such as addition, subtraction, multiplication, and division as transformations of those matrices and showed the associative and distributive properties held. Cayley investigated and demonstrated the non-commutative property of matrix multiplication as well as the commutative property of matrix addition.Early matrix theory had limited the use of arrays almost exclusively to determinants and Arthur Cayley's abstract matrix operations were revolutionary. He was instrumental in proposing a matrix concept independent of equation systems. In 1858Cayleypublished hisA memoir on the theory of matricesin which he proposed and demonstrated theCayley–Hamilton theorem.

The English mathematicianCuthbert Edmund Culliswas the first to use modern bracket notation for matrices in 1913 and he simultaneously demonstrated the first significant use of the notationA= [a_i,j]to represent a matrix wherea_i,jrefers to theith row and thejth column.

The modern study of determinants sprang from several sources.Number-theoreticalproblems ledGaussto relate coefficients ofquadratic forms,that is, expressions such asx²+xy− 2y²,andlinear mapsin three dimensions to matrices.Eisensteinfurther developed these notions, including the remark that, in modern parlance,matrix productsarenon-commutative.Cauchywas the first to prove general statements about determinants, using as the definition of the determinant of a matrixA= [a_{i, j}]the following: replace the powersa^k
_jbya_jkin thepolynomial

$a_{1}a_{2}\cdots a_{n}\prod _{i<j}(a_{j}-a_{i})\;$,

where$\textstyle \prod$denotes theproductof the indicated terms. He also showed, in 1829, that theeigenvaluesof symmetric matrices are real.Jacobistudied "functional determinants" —later calledJacobi determinantsby Sylvester—which can be used to describe geometric transformations at a local (orinfinitesimal) level, seeabove.Kronecker'sVorlesungen über die Theorie der DeterminantenandWeierstrass'Zur Determinantentheorie,both published in 1903, first treated determinantsaxiomatically,as opposed to previous more concrete approaches such as the mentioned formula of Cauchy. At that point, determinants were firmly established.

Many theorems were first established for small matrices only, for example, theCayley–Hamilton theoremwas proved for 2×2 matrices by Cayley in the aforementioned memoir, and byHamiltonfor 4×4 matrices.Frobenius,working onbilinear forms,generalized the theorem to all dimensions (1898). Also at the end of the 19th century, theGauss–Jordan elimination(generalizing a special case now known asGauss elimination) was established byWilhelm Jordan.In the early 20th century, matrices attained a central role in linear algebra,partially due to their use in the classification of thehypercomplex numbersystems of the previous century.

The inception ofmatrix mechanicsbyHeisenberg,BornandJordanled to studying matrices with infinitely many rows and columns.Later,von Neumanncarried out themathematical formulation of quantum mechanics,by further developingfunctional analyticnotions such aslinear operatorsonHilbert spaces,which, very roughly speaking, correspond toEuclidean space,but with an infinity ofindependent directions.

Other historical usages of the word "matrix" in mathematics

The word has been used in unusual ways by at least two authors of historical importance.

Bertrand RussellandAlfred North Whiteheadin theirPrincipia Mathematica(1910–1913) use the word "matrix" in the context of theiraxiom of reducibility.They proposed this axiom as a means to reduce any function to one of lower type, successively, so that at the "bottom" (0 order) the function is identical to itsextension:

Let us give the name ofmatrixto any function, of however many variables, that does not involve anyapparent variables.Then, any possible function other than a matrix derives from a matrix using generalization, that is, by considering the proposition that the function in question is true with all possible values or with some value of one of the arguments, the other argument or arguments remaining undetermined.

For example, a functionΦ(x, y)of two variablesxandycan be reduced to acollectionof functions of a single variable, for example,y,by "considering" the function for all possible values of "individuals"a_isubstituted in place of a variablex.And then the resulting collection of functions of the single variabley,that is,∀a_i:Φ(a_i,y),can be reduced to a "matrix" of values by "considering" the function for all possible values of "individuals"b_isubstituted in place of variabley: $$\forall b_{j}\forall a_{i}:\phi (a_{i},b_{j}).$$

Alfred Tarskiin his 1946Introduction to Logicused the word "matrix" synonymously with the notion oftruth tableas used in mathematical logic.

See also

• List of named matrices
• Algebraic multiplicity– Multiplicity of an eigenvalue as a root of the characteristic polynomial
• Geometric multiplicity– Dimension of the eigenspace associated with an eigenvalue
• Gram–Schmidt process– Orthonormalization of a set of vectors
• Irregular matrix
• Matrix calculus– Specialized notation for multivariable calculus
• Matrix function– Function that maps matrices to matricesPages displaying short descriptions of redirect targets
• Matrix multiplication algorithm
• Tensor— A generalization of matrices with any number of indices
• Bohemian matrices– Set of matrices
• Category of matrices— The algebraic structure formed by matrices and their multiplication

References

• Anton, Howard (1987),Elementary Linear Algebra(5th ed.), New York:Wiley,ISBN0-471-84819-0
• Arnold, Vladimir I.;Cooke, Roger(1992),Ordinary differential equations,Berlin, DE; New York, NY:Springer-Verlag,ISBN978-3-540-54813-3
• Artin, Michael(1991),Algebra,Prentice Hall,ISBN978-0-89871-510-1
• Association for Computing Machinery (1979),Computer Graphics,Tata McGraw–Hill,ISBN978-0-07-059376-3
• Baker, Andrew J. (2003),Matrix Groups: An Introduction to Lie Group Theory,Berlin, DE; New York, NY: Springer-Verlag,ISBN978-1-85233-470-3
• Bau III, David;Trefethen, Lloyd N.(1997),Numerical linear algebra,Philadelphia, PA: Society for Industrial and Applied Mathematics,ISBN978-0-89871-361-9
• Beauregard, Raymond A.; Fraleigh, John B. (1973),A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields,Boston:Houghton Mifflin Co.,ISBN0-395-14017-X
• Bretscher, Otto (2005),Linear Algebra with Applications(3rd ed.), Prentice Hall
• Bronson, Richard (1970),Matrix Methods: An Introduction,New York:Academic Press,LCCN70097490
• Bronson, Richard (1989),Schaum's outline of theory and problems of matrix operations,New York:McGraw–Hill,ISBN978-0-07-007978-6
• Brown, William C. (1991),Matrices and vector spaces,New York, NY:Marcel Dekker,ISBN978-0-8247-8419-5
• Coburn, Nathaniel (1955),Vector and tensor analysis,New York, NY: Macmillan,OCLC1029828
• Conrey, J. Brian (2007),Ranks of elliptic curves and random matrix theory,Cambridge University Press,ISBN978-0-521-69964-8
• Fraleigh, John B. (1976),A First Course In Abstract Algebra(2nd ed.), Reading:Addison-Wesley,ISBN0-201-01984-1
• Fudenberg, Drew;Tirole, Jean(1983),Game Theory,MIT Press
• Gilbarg, David;Trudinger, Neil S.(2001),Elliptic partial differential equations of second order(2nd ed.), Berlin, DE; New York, NY: Springer-Verlag,ISBN978-3-540-41160-4
• Godsil, Chris;Royle, Gordon(2004),Algebraic Graph Theory,Graduate Texts in Mathematics, vol. 207, Berlin, DE; New York, NY: Springer-Verlag,ISBN978-0-387-95220-8
• Golub, Gene H.;Van Loan, Charles F.(1996),Matrix Computations(3rd ed.), Johns Hopkins,ISBN978-0-8018-5414-9
• Greub, Werner Hildbert (1975),Linear algebra,Graduate Texts in Mathematics, Berlin, DE; New York, NY: Springer-Verlag,ISBN978-0-387-90110-7
• Halmos, Paul Richard(1982),A Hilbert space problem book,Graduate Texts in Mathematics, vol. 19 (2nd ed.), Berlin, DE; New York, NY: Springer-Verlag,ISBN978-0-387-90685-0,MR0675952
• Horn, Roger A.;Johnson, Charles R.(1985),Matrix Analysis,Cambridge University Press,ISBN978-0-521-38632-6
• Householder, Alston S. (1975),The theory of matrices in numerical analysis,New York, NY:Dover Publications,MR0378371
• Kreyszig, Erwin (1972),Advanced Engineering Mathematics(3rd ed.), New York:Wiley,ISBN0-471-50728-8.
• Krzanowski, Wojtek J. (1988),Principles of multivariate analysis,Oxford Statistical Science Series, vol. 3, The Clarendon Press Oxford University Press,ISBN978-0-19-852211-9,MR0969370
• Itô, Kiyosi, ed. (1987),Encyclopedic dictionary of mathematics. Vol. I-IV(2nd ed.), MIT Press,ISBN978-0-262-09026-1,MR0901762
• Lang, Serge(1969),Analysis II,Addison-Wesley
• Lang, Serge (1987a),Calculus of several variables(3rd ed.), Berlin, DE; New York, NY: Springer-Verlag,ISBN978-0-387-96405-8
• Lang, Serge (1987b),Linear algebra,Berlin, DE; New York, NY: Springer-Verlag,ISBN978-0-387-96412-6
• Lang, Serge(2002),Algebra,Graduate Texts in Mathematics,vol. 211 (Revised third ed.), New York: Springer-Verlag,ISBN978-0-387-95385-4,MR1878556
• Latouche, Guy; Ramaswami, Vaidyanathan (1999),Introduction to matrix analytic methods in stochastic modeling(1st ed.), Philadelphia, PA: Society for Industrial and Applied Mathematics,ISBN978-0-89871-425-8
• Manning, Christopher D.; Schütze, Hinrich (1999),Foundations of statistical natural language processing,MIT Press,ISBN978-0-262-13360-9
• Mehata, K. M.; Srinivasan, S. K. (1978),Stochastic processes,New York, NY: McGraw–Hill,ISBN978-0-07-096612-3
• Mirsky, Leonid(1990),An Introduction to Linear Algebra,Courier Dover Publications,ISBN978-0-486-66434-7
• Nering, Evar D. (1970),Linear Algebra and Matrix Theory(2nd ed.), New York:Wiley,LCCN76-91646
• Nocedal, Jorge; Wright, Stephen J. (2006),Numerical Optimization(2nd ed.), Berlin, DE; New York, NY: Springer-Verlag, p. 449,ISBN978-0-387-30303-1
• Oualline, Steve (2003),Practical C++ programming,O'Reilly,ISBN978-0-596-00419-4
• Perrone, Paolo (2024),Starting Category Theory,World Scientific,doi:10.1142/9789811286018_0005,ISBN978-981-12-8600-1
• Press, William H.; Flannery, Brian P.;Teukolsky, Saul A.;Vetterling, William T. (1992),"LU Decomposition and Its Applications"(PDF),Numerical Recipes in FORTRAN: The Art of Scientific Computing(2nd ed.), Cambridge University Press, pp. 34–42, archived from the original on 2009-09-06{{citation}}:CS1 maint: unfit URL (link)
• Protter, Murray H.; Morrey, Charles B. Jr. (1970),College Calculus with Analytic Geometry(2nd ed.), Reading:Addison-Wesley,LCCN76087042
• Punnen, Abraham P.; Gutin, Gregory (2002),The traveling salesman problem and its variations,Boston, MA: Kluwer Academic Publishers,ISBN978-1-4020-0664-7
• Reichl, Linda E.(2004),The transition to chaos: conservative classical systems and quantum manifestations,Berlin, DE; New York, NY: Springer-Verlag,ISBN978-0-387-98788-0
• Rowen, Louis Halle (2008),Graduate Algebra: noncommutative view,Providence, RI:American Mathematical Society,ISBN978-0-8218-4153-2
• Šolin, Pavel (2005),Partial Differential Equations and the Finite Element Method,Wiley-Interscience,ISBN978-0-471-76409-0
• Stinson, Douglas R. (2005),Cryptography,Discrete Mathematics and its Applications, Chapman & Hall/CRC,ISBN978-1-58488-508-5
• Stoer, Josef; Bulirsch, Roland (2002),Introduction to Numerical Analysis(3rd ed.), Berlin, DE; New York, NY: Springer-Verlag,ISBN978-0-387-95452-3
• Ward, J. P. (1997),Quaternions and Cayley numbers,Mathematics and its Applications, vol. 403, Dordrecht, NL: Kluwer Academic Publishers Group,doi:10.1007/978-94-011-5768-1,ISBN978-0-7923-4513-8,MR1458894
• Wolfram, Stephen(2003),The Mathematica Book(5th ed.), Champaign, IL: Wolfram Media,ISBN978-1-57955-022-6

Physics references

• Bohm, Arno (2001),Quantum Mechanics: Foundations and Applications,Springer,ISBN0-387-95330-2
• Burgess, Cliff; Moore, Guy (2007),The Standard Model. A Primer,Cambridge University Press,ISBN978-0-521-86036-9
• Guenther, Robert D. (1990),Modern Optics,John Wiley,ISBN0-471-60538-7
• Itzykson, Claude; Zuber, Jean-Bernard (1980),Quantum Field Theory,McGraw–Hill,ISBN0-07-032071-3
• Riley, Kenneth F.; Hobson, Michael P.; Bence, Stephen J. (1997),Mathematical methods for physics and engineering,Cambridge University Press,ISBN0-521-55506-X
• Schiff, Leonard I. (1968),Quantum Mechanics(3rd ed.), McGraw–Hill
• Weinberg, Steven (1995),The Quantum Theory of Fields. Volume I: Foundations,Cambridge University Press,ISBN0-521-55001-7
• Wherrett, Brian S. (1987),Group Theory for Atoms, Molecules and Solids,Prentice–Hall International,ISBN0-13-365461-3
• Zabrodin, Anton; Brezin, Édouard; Kazakov, Vladimir; Serban, Didina; Wiegmann, Paul (2006),Applications of Random Matrices in Physics (NATO Science Series II: Mathematics, Physics and Chemistry),Berlin, DE; New York, NY:Springer-Verlag,ISBN978-1-4020-4530-1

Historical references

• A. CayleyA memoir on the theory of matrices.Phil. Trans. 148 1858 17–37; Math. Papers II 475–496
• Bôcher, Maxime(2004),Introduction to higher algebra,New York, NY:Dover Publications,ISBN978-0-486-49570-5,reprint of the 1907 original edition
• Cayley, Arthur(1889),The collected mathematical papers of Arthur Cayley,vol. I (1841–1853),Cambridge University Press,pp. 123–126
• Dieudonné, Jean,ed. (1978),Abrégé d'histoire des mathématiques 1700-1900,Paris, FR: Hermann
• Hawkins, Thomas (1975), "Cauchy and the spectral theory of matrices",Historia Mathematica,2:1–29,doi:10.1016/0315-0860(75)90032-4,ISSN0315-0860,MR0469635
• Knobloch, Eberhard(1994), "From Gauss to Weierstrass: determinant theory and its historical evaluations",The intersection of history and mathematics,Science Networks Historical Studies, vol. 15, Basel, Boston, Berlin: Birkhäuser, pp. 51–66,MR1308079
• Kronecker, Leopold(1897),Hensel, Kurt(ed.),Leopold Kronecker's Werke,Teubner
• Mehra, Jagdish;Rechenberg, Helmut(1987),The Historical Development of Quantum Theory(1st ed.), Berlin, DE; New York, NY:Springer-Verlag,ISBN978-0-387-96284-9
• Shen, Kangshen; Crossley, John N.; Lun, Anthony Wah-Cheung (1999),Nine Chapters of the Mathematical Art, Companion and Commentary(2nd ed.),Oxford University Press,ISBN978-0-19-853936-0
• Weierstrass, Karl(1915),Collected works,vol. 3

Further reading

• "Matrix",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• The Matrix Cookbook(PDF),retrieved24 March2014
• Brookes, Mike (2005),The Matrix Reference Manual,London:Imperial College,archived fromthe originalon 16 December 2008,retrieved10 Dec2008

External links

• MacTutor: Matrices and determinants
• Matrices and Linear Algebra on the Earliest Uses Pages
• Earliest Uses of Symbols for Matrices and Vectors