Semi-major and semi-minor axes

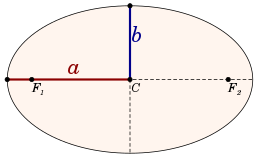
Ingeometry,themajor axisof anellipseis its longestdiameter:aline segmentthat runs through the center and bothfoci,with ends at the two most widely separated points of theperimeter.Thesemi-major axis(major semiaxis) is the longestsemidiameteror one half of the major axis, and thus runs from the centre, through afocus,and to the perimeter. Thesemi-minor axis(minor semiaxis) of an ellipse orhyperbolais a line segment that is atright angleswith the semi-major axis and has one end at the center of theconic section.For the special case of a circle, the lengths of the semi-axes are both equal to theradiusof the circle.

The length of the semi-major axis $a$ of an ellipse is related to the semi-minor axis's length $b$ through theeccentricity $e$ and thesemi-latus rectum $\ell$ ,as follows:

{\begin{aligned}b&=a{\sqrt {1-e^{2}}},\\\ell &=a(1-e^{2}),\\a\ell &=b^{2}.\end{aligned}}

The semi-major axis of ahyperbolais, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the center to eithervertexof the hyperbola.

Aparabolacan be obtained as the limit of a sequence of ellipses where one focus is kept fixed as the other is allowed to move arbitrarily far away in one direction, keeping $\ell$ fixed. Thus $a$ and $b$ tend to infinity, $a$ faster than $b$ .

The major and minor axes are theaxes of symmetryfor the curve: in an ellipse, the minor axis is the shorter one; in a hyperbola, it is the one that does not intersect the hyperbola.

Ellipse

The equation of an ellipse is

{\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}{b^{2}}}=1,

where (h,k) is the center of the ellipse inCartesian coordinates,in which an arbitrary point is given by (x,y).

The semi-major axis is the mean value of the maximum and minimum distances $r_{\text{max}}$ and $r_{\text{min}}$ of the ellipse from a focus — that is, of the distances from a focus to the endpoints of the major axis

a={\frac {r_{\text{max}}+r_{\text{min}}}{2}}.

In astronomy these extreme points are calledapsides.^[1]

The semi-minor axis of an ellipse is thegeometric meanof these distances:

b={\sqrt {r_{\text{max}}r_{\text{min}}}}.

Theeccentricityof an ellipse is defined as

e={\sqrt {1-{\frac {b^{2}}{a^{2}}}}},

so

r_{\text{min}}=a(1-e),\quad r_{\text{max}}=a(1+e).

Now consider the equation inpolar coordinates,with one focus at the origin and the other on the $\theta =\pi$ direction:

r(1+e\cos \theta )=\ell.

The mean value of $r=\ell /(1-e)$ and $r=\ell /(1+e)$ ,for $\theta =\pi$ and $\theta =0$ is

a={\frac {\ell }{1-e^{2}}}.

In an ellipse, the semi-major axis is thegeometric meanof the distance from the center to either focus and the distance from the center to either directrix.

The semi-minor axis of an ellipse runs from the center of the ellipse (a point halfway between and on the line running between thefoci) to the edge of the ellipse. The semi-minor axis is half of the minor axis. The minor axis is the longest line segment perpendicular to the major axis that connects two points on the ellipse's edge.

The semi-minor axis $b$ is related to the semi-major axis $a$ through the eccentricity $e$ and thesemi-latus rectum $\ell$ ,as follows:

{\begin{aligned}b&=a{\sqrt {1-e^{2}}},\\a\ell &=b^{2}.\end{aligned}}

Aparabolacan be obtained as the limit of a sequence of ellipses where one focus is kept fixed as the other is allowed to move arbitrarily far away in one direction, keeping $\ell$ fixed. Thus $a$ and $b$ tend to infinity, $a$ faster than $b$ .

The length of the semi-minor axis could also be found using the following formula:^[2]

2b={\sqrt {(p+q)^{2}-f^{2}}},

where $f$ is the distance between the foci, $p$ and $q$ are the distances from each focus to any point in the ellipse.

Hyperbola

The semi-major axis of ahyperbolais, depending on the convention, plus or minus one half of the distance between the two branches; if this is $a$ in the x-direction the equation is:^[3]

{\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1.

In terms of the semi-latus rectum and the eccentricity, we have

a={\ell \over e^{2}-1}.

The transverse axis of a hyperbola coincides with the major axis.^[4]

In a hyperbola, a conjugate axis or minor axis of length $2b$ ,corresponding to the minor axis of an ellipse, can be drawn perpendicular to the transverse axis or major axis, the latter connecting the twovertices(turning points) of the hyperbola, with the two axes intersecting at the center of the hyperbola. The endpoints $(0,\pm b)$ of the minor axis lie at the height of the asymptotes over/under the hyperbola's vertices. Either half of the minor axis is called the semi-minor axis, of length $b$ .Denoting the semi-major axis length (distance from the center to a vertex) as $a$ ,the semi-minor and semi-major axes' lengths appear in the equation of the hyperbola relative to these axes as follows:

{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1.

The semi-minor axis is also the distance from one of focuses of the hyperbola to an asymptote. Often called theimpact parameter,this is important in physics and astronomy, and measure the distance a particle will miss the focus by if its journey is unperturbed by the body at the focus.^{[citation needed]}

The semi-minor axis and the semi-major axis are related through the eccentricity, as follows:

b=a{\sqrt {e^{2}-1}}.

^[5]

Note that in a hyperbola $b$ can be larger than $a$ .^[6]

Astronomy

Orbital period

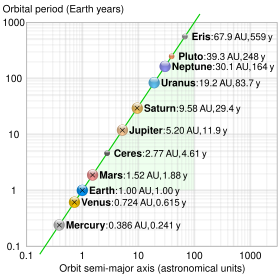
Inastrodynamicstheorbital period $T$ of a small body orbiting a central body in a circular or elliptical orbit is:^[1]

T=2\pi {\sqrt {\frac {a^{3}}{\mu }}},

where:

a

is the length of the orbit's semi-major axis,

\mu

is thestandard gravitational parameterof the central body.

Note that for all ellipses with a given semi-major axis, the orbital period is the same, disregarding their eccentricity.

Thespecific angular momentum $h$ of a small body orbiting a central body in a circular or elliptical orbit is^[1]

h={\sqrt {a\mu (1-e^{2})}},

where:

a

and

\mu

are as defined above,

e

is the eccentricity of the orbit.

Inastronomy,the semi-major axis is one of the most importantorbital elementsof anorbit,along with itsorbital period.ForSolar Systemobjects, the semi-major axis is related to the period of the orbit byKepler's third law(originallyempiricallyderived):^[1]

T^{2}\propto a^{3},

where $T$ is the period, and $a$ is the semi-major axis. This form turns out to be a simplification of the general form for thetwo-body problem,as determined byNewton:^[1]

T^{2}={\frac {4\pi ^{2}}{G(M+m)}}a^{3},

where $G$ is thegravitational constant, $M$ is themassof the central body, and $m$ is the mass of the orbiting body. Typically, the central body's mass is so much greater than the orbiting body's, that $m$ may be ignored. Making that assumption and using typical astronomy units results in the simpler form Kepler discovered.

The orbiting body's path around thebarycenterand its path relative to its primary are both ellipses.^[1]The semi-major axis is sometimes used in astronomy as the primary-to-secondary distance when the mass ratio of the primary to the secondary is significantly large ( $M\gg m$ ); thus, the orbital parameters of the planets are given in heliocentric terms. The difference between the primocentric and "absolute" orbits may best be illustrated by looking at the Earth–Moon system. The mass ratio in this case is81.30059.The Earth–Moon characteristic distance, the semi-major axis of thegeocentriclunar orbit, is 384,400 km. (Given the lunar orbit's eccentricitye= 0.0549, its semi-minor axis is 383,800 km. Thus the Moon's orbit is almost circular.) Thebarycentriclunar orbit, on the other hand, has a semi-major axis of 379,730 km, the Earth's counter-orbit taking up the difference, 4,670 km. The Moon's average barycentric orbital speed is 1.010 km/s, whilst the Earth's is 0.012 km/s. The total of these speeds gives a geocentric lunar average orbital speed of 1.022 km/s; the same value may be obtained by considering just the geocentric semi-major axis value.^{[citation needed]}

Average distance

It is often said that the semi-major axis is the "average" distance between the primary focus of the ellipse and the orbiting body. This is not quite accurate, because it depends on what the average is taken over. The time- and angle-averaged distance of the orbiting body can vary by 50-100% from the orbital semi-major axis, depending on the eccentricity.^[7]

averaging the distance over theeccentric anomalyindeed results in the semi-major axis.
averaging over thetrue anomaly(the true orbital angle, measured at the focus) results in the semi-minor axis $b=a{\sqrt {1-e^{2}}}$ .
averaging over themean anomaly(the fraction of the orbital period that has elapsed since pericentre, expressed as an angle) gives the time-average $a\left(1+{\frac {e^{2}}{2}}\right)\,$ .

The time-averaged value of the reciprocal of the radius, $r^{-1}$ ,is $a^{-1}$ .

Energy; calculation of semi-major axis from state vectors

Inastrodynamics,the semi-major axis $a$ can be calculated fromorbital state vectors:

a=-{\frac {\mu }{2\varepsilon }}

for anelliptical orbitand, depending on the convention, the same or

a={\frac {\mu }{2\varepsilon }}

for ahyperbolic trajectory,and

\varepsilon ={\frac {v^{2}}{2}}-{\frac {\mu }{|\mathbf {r} |}}

(specific orbital energy) and

\mu =GM,

(standard gravitational parameter), where:

v

is orbital velocity fromvelocity vectorof an orbiting object,

r

is acartesian position vectorof an orbiting object in coordinates of areference framewith respect to which the elements of the orbit are to be calculated (e.g. geocentric equatorial for an orbit around Earth, or heliocentric ecliptic for an orbit around the Sun),

G

is thegravitational constant,

M

is the mass of the gravitating body, and

\varepsilon

is the specific energy of the orbiting body.

Note that for a given amount of total mass, the specific energy and the semi-major axis are always the same, regardless of eccentricity or the ratio of the masses. Conversely, for a given total mass and semi-major axis, the totalspecific orbital energyis always the same. This statement will always be true under any given conditions.^{[citation needed]}

Semi-major and semi-minor axes of the planets' orbits

Planet orbits are always cited as prime examples of ellipses (Kepler's first law). However, the minimal difference between the semi-major and semi-minor axes shows that they are virtually circular in appearance. That difference (or ratio) is based on the eccentricity and is computed as ${\frac {a}{b}}={\frac {1}{\sqrt {1-e^{2}}}}$ ,which for typical planet eccentricities yields very small results.

The reason for the assumption of prominent elliptical orbits lies probably in the much larger difference between aphelion and perihelion. That difference (or ratio) is also based on the eccentricity and is computed as ${\frac {r_{\text{a}}}{r_{\text{p}}}}={\frac {1+e}{1-e}}$ .Due to the large difference between aphelion and perihelion,Kepler's second lawis easily visualized.

	Eccentricity	Semi-major axisa(AU)	Semi-minor axisb(AU)	Difference (%)	Perihelion(AU)	Aphelion(AU)	Difference (%)
Mercury	0.206	0.38700	0.37870	2.2	0.307	0.467	52
Venus	0.007	0.72300	0.72298	0.002	0.718	0.728	1.4
Earth	0.017	1.00000	0.99986	0.014	0.983	1.017	3.5
Mars	0.093	1.52400	1.51740	0.44	1.382	1.666	21
Jupiter	0.049	5.20440	5.19820	0.12	4.950	5.459	10
Saturn	0.057	9.58260	9.56730	0.16	9.041	10.124	12
Uranus	0.046	19.21840	19.19770	0.11	18.330	20.110	9.7
Neptune	0.010	30.11000	30.10870	0.004	29.820	30.400	1.9

1 AU (astronomical unit) equals 149.6 million km.

References

^^a ^b ^c ^d ^e ^fLissauer, Jack J.; de Pater, Imke (2019).Fundamental Planetary Sciences: physics, chemistry, and habitability.New York: Cambridge University Press. pp. 24–31.ISBN 9781108411981.
^"Major / Minor axis of an ellipse",Math Open Reference, 12 May 2013.
^Weisstein, Eric W."Ellipse".mathworld.wolfram.com.Retrieved2024-08-20.
^"7.1 Alternative Characterization".www.geom.uiuc.edu.Archived fromthe originalon 2018-10-24.Retrieved2007-09-06.
^"The Geometry of Orbits: Ellipses, Parabolas, and Hyperbolas".www.bogan.ca.
^"7.1 Alternative Characterization".Archived fromthe originalon 2018-10-24.Retrieved2007-09-06.
^Williams, Darren M. (November 2003). "Average distance between a star and planet in an eccentric orbit".American Journal of Physics.71(11): 1198–1200.Bibcode:2003AmJPh..71.1198W.doi:10.1119/1.1578073.

External links

Semi-major and semi-minor axes of an ellipseWith interactive animation

[lissauer2019-1] Lissauer, Jack J.; de Pater, Imke (2019).Fundamental Planetary Sciences: physics, chemistry, and habitability.New York: Cambridge University Press. pp. 24–31.ISBN 9781108411981.

[2] "Major / Minor axis of an ellipse",Math Open Reference, 12 May 2013.

[3] Weisstein, Eric W."Ellipse".mathworld.wolfram.com.Retrieved2024-08-20.

[4] "7.1 Alternative Characterization".www.geom.uiuc.edu.Archived fromthe originalon 2018-10-24.Retrieved2007-09-06.

[5] "The Geometry of Orbits: Ellipses, Parabolas, and Hyperbolas".www.bogan.ca.

[6] "7.1 Alternative Characterization".Archived fromthe originalon 2018-10-24.Retrieved2007-09-06.

[7] Williams, Darren M. (November 2003). "Average distance between a star and planet in an eccentric orbit".American Journal of Physics.71(11): 1198–1200.Bibcode:2003AmJPh..71.1198W.doi:10.1119/1.1578073.

[1]

[2]

[3]

[4]

[5]

[6]

[7]