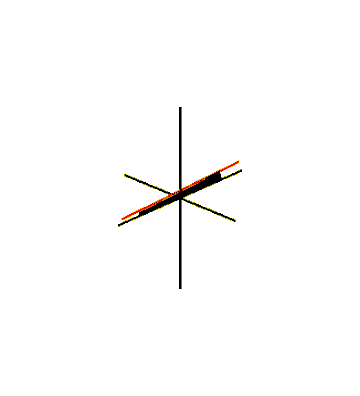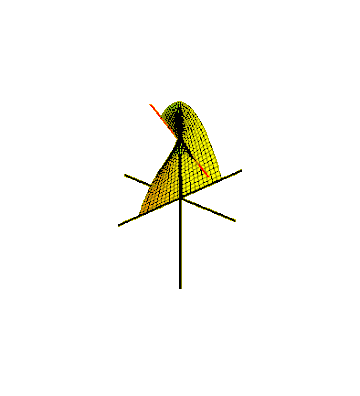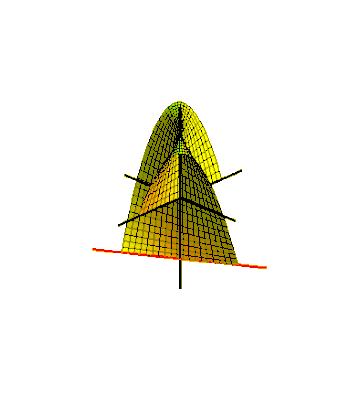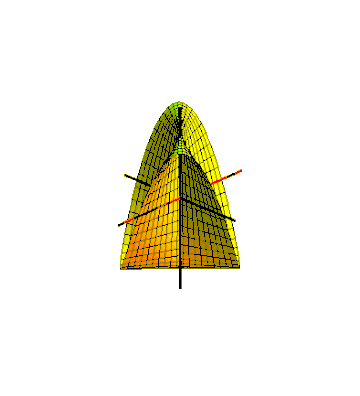Möbius strip

Inmathematics,aMöbius strip,Möbius band,orMöbius loop^[a]is asurfacethat can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered byJohann Benedict ListingandAugust Ferdinand Möbiusin 1858, but it had already appeared inRomanmosaics from the third centuryCE.The Möbius strip is anon-orientablesurface, meaning that within it one cannot consistently distinguishclockwisefrom counterclockwise turns. Every non-orientable surface contains a Möbius strip.

As an abstracttopological space,the Möbius strip can be embedded into three-dimensionalEuclidean spacein many different ways: a clockwise half-twist is different from a counterclockwise half-twist, and it can also be embedded with odd numbers of twists greater than one, or with aknottedcenterline. Any two embeddings with the same knot for the centerline and the same number and direction of twists aretopologically equivalent.All of these embeddings have only one side, but when embedded in other spaces, the Möbius strip may have two sides. It has only a singleboundary curve.

Several geometric constructions of the Möbius strip provide it with additional structure. It can be swept as aruled surfaceby a line segment rotating in a rotating plane, with or without self-crossings. A thin paper strip with its ends joined to form a Möbius strip can bend smoothly as adevelopable surfaceor befolded flat;the flattened Möbius strips include thetrihexaflexagon.The Sudanese Möbius strip is aminimal surfacein ahypersphere,and the Meeks Möbius strip is a self-intersecting minimal surface in ordinary Euclidean space. Both the Sudanese Möbius strip and another self-intersecting Möbius strip, the cross-cap, have a circular boundary. A Möbius strip without its boundary, called an open Möbius strip, can formsurfaces of constant curvature.Certain highly symmetric spaces whose points represent lines in the plane have the shape of a Möbius strip.

The many applications of Möbius strips includemechanical beltsthat wear evenly on both sides, dual-trackroller coasterswhose carriages alternate between the two tracks, andworld mapsprinted so thatantipodesappear opposite each other. Möbius strips appear in molecules and devices with novel electrical and electromechanical properties, and have been used to prove impossibility results insocial choice theory.In popular culture, Möbius strips appear in artworks byM. C. Escher,Max Bill,and others, and in the design of therecycling symbol.Many architectural concepts have been inspired by the Möbius strip, including the building design for theNASCAR Hall of Fame.Performers includingHarry Blackstone Sr.andThomas Nelson Downshave based stage magic tricks on the properties of the Möbius strip. ThecanonsofJ. S. Bachhave been analyzed using Möbius strips. Many works ofspeculative fictionfeature Möbius strips; more generally, a plot structure based on the Möbius strip, of events that repeat with a twist, is common in fiction.

History

Mosaic from ancientSentinumdepictingAionholding a Möbius strip

Chain pumpwith a Möbius drive chain, byIsmail al-Jazari(1206)

The discovery of the Möbius strip as a mathematical object is attributed independently to the German mathematiciansJohann Benedict ListingandAugust Ferdinand Möbiusin1858.^[2]However, it had been known long before, both as a physical object and in artistic depictions; in particular, it can be seen in several Roman mosaics from thethird century CE.^[3]^[4]In many cases these merely depict coiled ribbons as boundaries. When the number of coils is odd, these ribbons are Möbius strips, but for an even number of coils they are topologically equivalent tountwisted rings.Therefore, whether the ribbon is a Möbius strip may be coincidental, rather than a deliberate choice. In at least one case, a ribbon with different colors on different sides was drawn with an odd number of coils, forcing its artist to make a clumsy fix at the point where the colors did notmatch up.^[3]Another mosaic from the town ofSentinum(depicted) shows thezodiac,held by the godAion,as a band with only a single twist. There is no clear evidence that the one-sidedness of this visual representation of celestial time was intentional; it could have been chosen merely as a way to make all of the signs of the zodiac appear on the visible side of the strip. Some other ancient depictions of theourobourosor offigure-eight-shaped decorations are also alleged to depict Möbius strips, but whether they were intended to depict flat strips of any type isunclear.^[4]

Independently of the mathematical tradition, machinists have long known thatmechanical beltswear half as quickly when they form Möbius strips, because they use the entire surface of the belt rather than only the inner surface of an untwisted belt.^[3]Additionally, such a belt may be less prone to curling from side to side. An early written description of this technique dates to 1871, which is after the first mathematical publications regarding the Möbius strip. Much earlier, an image of achain pumpin a work ofIsmail al-Jazarifrom 1206 depicts a Möbius strip configuration for its drivechain.^[4]Another use of this surface was made by seamstresses in Paris (at an unspecified date): they initiated novices by requiring them to stitch a Möbius strip as a collar onto agarment.^[3]

Properties

The Möbius strip has several curious properties. It is anon-orientable surface:if an asymmetric two-dimensional object slides one time around the strip, it returns to its starting position as its mirror image. In particular, a curved arrow pointing clockwise (↻) would return as an arrow pointing counterclockwise (↺), implying that, within the Möbius strip, it is impossible to consistently define what it means to be clockwise or counterclockwise. It is the simplest non-orientable surface: any other surface is non-orientable if and only if it has a Möbius strip as asubset.^[5]Relatedly, when embedded intoEuclidean space,the Möbius strip has only one side. A three-dimensional object that slides one time around the surface of the strip is not mirrored, but instead returns to the same point of the strip on what appears locally to be its other side, showing that both positions are really part of a single side. This behavior is different from familiarorientable surfacesin three dimensions such as those modeled by flat sheets of paper, cylindrical drinking straws, or hollow balls, for which one side of the surface is not connected to the other.^[6]However, this is a property of its embedding into space rather than an intrinsic property of the Möbius strip itself: there exist other topological spaces in which the Möbius strip can be embedded so that it has twosides.^[7]For instance, if the front and back faces of a cube are glued to each other with a left-right mirror reflection, the result is a three-dimensional topological space (theCartesian productof a Möbius strip with an interval) in which the top and bottom halves of the cube can be separated from each other by a two-sided Möbiusstrip.^[b]In contrast to disks, spheres, and cylinders, for which it is possible to simultaneously embed anuncountable setofdisjointcopies into three-dimensional space, only a countable number of Möbius strips can be simultaneouslyembedded.^[9]^[10]^[11]

A path along the edge of a Möbius strip, traced until it returns to its starting point on the edge, includes all boundary points of the Möbius strip in a single continuous curve. For a Möbius strip formed by gluing and twisting a rectangle, it has twice the length of the centerline of the strip. In this sense, the Möbius strip is different from an untwisted ring and like a circular disk in having only oneboundary.^[6]A Möbius strip in Euclidean space cannot be moved or stretched into its mirror image; it is achiralobject with right- orleft-handedness.^[12]Möbius strips with odd numbers of half-twists greater than one, or that are knotted before gluing, are distinct as embedded subsets of three-dimensional space, even though they are all equivalent as two-dimensional topologicalsurfaces.^[13]More precisely, two Möbius strips are equivalently embedded in three-dimensional space when their centerlines determine the same knot and they have the same number of twists as eachother.^[14]With an even number of twists, however, one obtains a different topological surface, called theannulus.^[15]

The Möbius strip can be continuously transformed into its centerline, by making it narrower while fixing the points on the centerline. This transformation is an example of adeformation retraction,and its existence means that the Möbius strip has many of the same properties as its centerline, which is topologically a circle. In particular, itsfundamental groupis the same as the fundamental group of a circle, aninfinite cyclic group.Therefore, paths on the Möbius strip that start and end at the same point can be distinguished topologically (up tohomotopy) only by the number of times they loop around the strip.^[16]

Cutting the centerline produces a double-length two-sided (non-Möbius) strip

A single off-center cut produces a Möbius strip (purple) linked with a double-length two-sided strip

Cutting a Möbius strip along the centerline with a pair of scissors yields one long strip with four half-twists in it (relative to an untwisted annulus or cylinder) rather than two separate strips. Two of the half-twists come from the fact that this thinner strip goes two times through the half-twist in the original Möbius strip, and the other two come from the way the two halves of the thinner strip wrap around each other. The result is not a Möbius strip, but instead is topologically equivalent to a cylinder. Cutting this double-twisted strip again along its centerline produces two linked double-twisted strips. If, instead, a Möbius strip is cut lengthwise, a third of the way across its width, it produces two linked strips. One of the two is a central, thinner, Möbius strip, while the other has twohalf-twists.^[6]These interlinked shapes, formed by lengthwise slices of Möbius strips with varying widths, are sometimes calledparadromicrings.^[17]^[18]

Subdivision into six mutually-adjacent regions, bounded byTietze's graph

Solution to thethree utilities problemon a Möbius strip

The Möbius strip can be cut into six mutually-adjacent regions, showing that maps on the surface of the Möbius strip can sometimes require six colors, in contrast to thefour color theoremfor theplane.^[19]Six colors are always enough. This result is part of theRingel–Youngs theorem,which states how many colors each topological surfaceneeds.^[20]The edges and vertices of these six regions formTietze's graph,which is adual graphon this surface for the six-vertexcomplete graphbut cannot bedrawn without crossings on a plane.Another family of graphs that can beembeddedon the Möbius strip, but not on the plane, are theMöbius ladders,the boundaries of subdivisions of the Möbius strip into rectangles meetingend-to-end.^[21]These include the utility graph, a six-vertexcomplete bipartite graphwhose embedding into the Möbius strip shows that, unlike in the plane, thethree utilities problemcan be solved on a transparent Möbiusstrip.^[22]TheEuler characteristicof the Möbius strip iszero,meaning that for any subdivision of the strip by vertices and edges into regions, the numbers $V$ , $E$ ,and $F$ of vertices, edges, and regions satisfy $V-E+F=0$ .For instance, Tietze's graph has $12$ vertices, $18$ edges, and $6$ regions; $12-18+6=0$ .^[19]

Constructions

There are many different ways of defining geometric surfaces with the topology of the Möbius strip, yielding realizations with additional geometric properties.

Sweeping a line segment

A Möbius strip swept out by a rotating line segment in a rotating plane

Plücker's conoidswept out by a different motion of a line segment

One way to embed the Möbius strip in three-dimensional Euclidean space is to sweep it out by a line segment rotating in a plane, which in turn rotates around one of itslines.^[23]For the swept surface to meet up with itself after a half-twist, the line segment should rotate around its center at half the angular velocity of the plane's rotation. This can be described as aparametric surfacedefined by equations for theCartesian coordinatesof its points, ${\begin{aligned}x(u,v)&=\left(1+{\frac {v}{2}}\cos {\frac {u}{2}}\right)\cos u\\y(u,v)&=\left(1+{\frac {v}{2}}\cos {\frac {u}{2}}\right)\sin u\\z(u,v)&={\frac {v}{2}}\sin {\frac {u}{2}}\\\end{aligned}}$ for $0\leq u<2\pi$ and $-1\leq v\leq 1$ , where one parameter $u$ describes the rotation angle of the plane around its central axis and the other parameter $v$ describes the position of a point along the rotating line segment. This produces a Möbius strip of width 1, whose center circle has radius 1, lies in the $xy$ -plane and is centered at $(0,0,0)$ .^[24]The same method can produce Möbius strips with any odd number of half-twists, by rotating the segment more quickly in its plane. The rotating segment sweeps out a circular disk in the plane that it rotates within, and the Möbius strip that it generates forms a slice through thesolid torusswept out by this disk. Because of the one-sidedness of this slice, the sliced torus remainsconnected.^[25]

A line or line segment swept in a different motion, rotating in a horizontal plane around the origin as it moves up and down, formsPlücker's conoidor cylindroid, an algebraicruled surfacein the form of a self-crossing Möbiusstrip.^[26]It has applications in the design ofgears.^[27]

Polyhedral surfaces and flat foldings

A strip of paper can form aflattenedMöbius strip in the plane by folding it at $60^{\circ }$ angles so that its center line lies along anequilateral triangle,and attaching the ends. The shortest strip for which this is possible consists of three equilateral triangles, folded at the edges where two triangles meet. Itsaspect ratio– the ratio of the strip's length^[c]to its width – is ${\sqrt {3}}\approx 1.73$ ,and the same folding method works for any larger aspectratio.^[28]^[29]For a strip of nine equilateral triangles, the result is atrihexaflexagon,which can be flexed to reveal different parts of itssurface.^[30]For strips too short to apply this method directly, one can first "accordion fold" the strip in its wide direction back and forth using an even number of folds. With two folds, for example, a $1\times 1$ strip would become a $1\times {\tfrac {1}{3}}$ folded strip whosecross sectionis in the shape of an 'N' and would remain an 'N' after a half-twist. The narrower accordion-folded strip can then be folded and joined in the same way that a longer stripwould be.^[28]^[29]

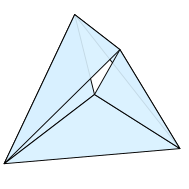
Five-vertex polyhedral and flat-folded Möbius strips

The Möbius strip can also be embedded as apolyhedral surfacein space or flat-folded in the plane, with only five triangular faces sharing five vertices. In this sense, it is simpler than thecylinder,which requires six triangles and six vertices, even when represented more abstractly as asimplicial complex.^[31]^[d]A five-triangle Möbius strip can be represented most symmetrically by five of the ten equilateral triangles of afour-dimensional regular simplex.This four-dimensional polyhedral Möbius strip is the onlytightMöbius strip, one that is fully four-dimensional and for which all cuts byhyperplanesseparate it into two parts that are topologically equivalent to disks orcircles.^[32]

Other polyhedral embeddings of Möbius strips include one with four convexquadrilateralsas faces, another with three non-convex quadrilateralfaces,^[33]and one using the vertices and center point of a regularoctahedron,with a triangularboundary.^[34]Every abstract triangulation of theprojective planecan be embedded into 3D as a polyhedral Möbius strip with a triangular boundary after removing one of itsfaces;^[35]an example is the six-vertex projective plane obtained by adding one vertex to the five-vertex Möbius strip, connected by triangles to each of its boundaryedges.^[31]However, not every abstract triangulation of the Möbius strip can be represented geometrically, as a polyhedralsurface.^[36]To be realizable, it is necessary and sufficient that there be no two disjoint non-contractible 3-cycles in thetriangulation.^[37]

Smoothly embedded rectangles

A rectangular Möbius strip, made by attaching the ends of a paper rectangle, can be embedded smoothly into three-dimensional space whenever its aspect ratio is greater than ${\sqrt {3}}\approx 1.73$ ,the same ratio as for the flat-folded equilateral-triangle version of the Möbiusstrip.^[38]This flat triangular embedding can lift to a smooth^[e]embedding in three dimensions, in which the strip lies flat in three parallel planes between three cylindrical rollers, each tangent to two of theplanes.^[38]Mathematically, a smoothly embedded sheet of paper can be modeled as adevelopable surface,that can bend but cannotstretch.^[39]^[40]As its aspect ratio decreases toward ${\sqrt {3}}$ ,all smooth embeddings seem to approach the same triangularform.^[41]

The lengthwise folds of an accordion-folded flat Möbius strip prevent it from forming a three-dimensional embedding in which the layers are separated from each other and bend smoothly without crumpling or stretching away from thefolds.^[29]Instead, unlike in the flat-folded case, there is a lower limit to the aspect ratio of smooth rectangular Möbius strips. Their aspect ratio cannot be less than $\pi /2\approx 1.57$ ,even if self-intersections are allowed. Self-intersecting smooth Möbius strips exist for any aspect ratio above thisbound.^[29]^[42]Without self-intersections, the aspect ratio must be atleast^[43] ${\frac {2}{3}}{\sqrt {3+2{\sqrt {3}}}}\approx 1.695.$

Unsolved problem in mathematics:

Can a

12\times 7

paper rectangle be glued end-to-end to form a smooth Möbius strip embedded in space? ^[f]

(more unsolved problems in mathematics)

For aspect ratios between this boundand ${\sqrt {3}}$ ,it has been an open problem whether smooth embeddings, without self-intersection,exist.^[29]^[42]^[43]In 2023,Richard Schwartzannounced a proof that they do not exist, but this result still awaits peer review and publication.^[44]^[45]If the requirement of smoothness is relaxed to allowcontinuously differentiablesurfaces, theNash–Kuiper theoremimplies that any two opposite edges of any rectangle can be glued to form an embedded Möbius strip, no matter how small the aspect ratiobecomes.^[g]The limiting case, a surface obtained from an infinite strip of the plane between two parallel lines, glued with the opposite orientation to each other, is called theunbounded Möbius stripor the realtautological line bundle.^[46]Although it has no smooth closed embedding into three-dimensional space, it can be embedded smoothly as a closed subset of four-dimensional Euclideanspace.^[47]

The minimum-energy shape of a smooth Möbius strip glued from a rectangle does not have a known analytic description, but can be calculated numerically, and has been the subject of much study inplate theorysince the initial work on this subject in 1930 byMichael Sadowsky.^[39]^[40]It is also possible to findalgebraic surfacesthat contain rectangular developable Möbiusstrips.^[48]^[49]

Making the boundary circular

Gluing two Möbius strips to form a Klein bottle

A projection of the Sudanese Möbius strip

The edge, orboundary,of a Möbius strip istopologically equivalentto acircle.In common forms of the Möbius strip, it has a different shape from a circle, but it isunknotted,and therefore the whole strip can be stretched without crossing itself to make the edge perfectlycircular.^[50]One such example is based on the topology of theKlein bottle,a one-sided surface with no boundary that cannot be embedded into three-dimensional space, but can beimmersed(allowing the surface to cross itself in certain restricted ways). A Klein bottle is the surface that results when two Möbius strips are glued together edge-to-edge, and – reversing that process – a Klein bottle can be sliced along a carefully chosen cut to produce two Möbiusstrips.^[51]For a form of the Klein bottle known as Lawson's Klein bottle, the curve along which it is sliced can be made circular, resulting in Möbius strips with circularedges.^[52]

Lawson's Klein bottle is a self-crossingminimal surfacein theunit hypersphereof 4-dimensional space, the set of points of the form $(\cos \theta \cos \phi,\sin \theta \cos \phi,\cos 2\theta \sin \phi,\sin 2\theta \sin \phi )$ for $0\leq \theta <\pi,0\leq \phi <2\pi$ .^[53]Half of this Klein bottle, the subset with $0\leq \phi <\pi$ ,gives a Möbius strip embedded in the hypersphere as a minimal surface with agreat circleas itsboundary.^[54]This embedding is sometimes called the "Sudanese Möbius strip" after topologists Sue Goodman and Daniel Asimov, who discovered it in the1970s.^[55]Geometrically Lawson's Klein bottle can be constructed by sweeping a great circle through a great-circular motion in the 3-sphere, and the Sudanese Möbius strip is obtained by sweeping a semicircle instead of a circle, or equivalently by slicing the Klein bottle along a circle that is perpendicular to all of the sweptcircles.^[52]^[56]Stereographic projectiontransforms this shape from a three-dimensional spherical space into three-dimensional Euclidean space, preserving the circularity of itsboundary.^[52]The most symmetric projection is obtained by using a projection point that lies on that great circle that runs through the midpoint of each of the semicircles, but produces an unbounded embedding with the projection point removed from itscenterline.^[54]Instead, leaving the Sudanese Möbius strip unprojected, in the 3-sphere, leaves it with an infinite group of symmetries isomorphic to theorthogonal group $\mathrm {O} (2)$ ,the group of symmetries of acircle.^[53]

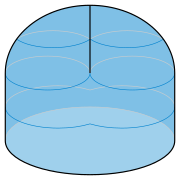
The Sudanese Möbius strip extends on all sides of its boundary circle, unavoidably if the surface is to avoid crossing itself. Another form of the Möbius strip, called thecross-caporcrosscap,also has a circular boundary, but otherwise stays on only one side of the plane of thiscircle,^[57]making it more convenient for attaching onto circular holes in other surfaces. In order to do so, it crosses itself. It can be formed by removing aquadrilateralfrom the top of a hemisphere, orienting the edges of the quadrilateral in alternating directions, and then gluing opposite pairs of these edges consistently with thisorientation.^[58]The two parts of the surface formed by the two glued pairs of edges cross each other with apinch pointlike that of aWhitney umbrellaat each end of the crossingsegment,^[59]the same topological structure seen in Plücker'sconoid.^[26]

Surfaces of constant curvature

The open Möbius strip is therelative interiorof a standard Möbius strip, formed by omitting the points on its boundary edge. It may be given aRiemannian geometryof constant positive, negative, or zeroGaussian curvature.The cases of negative and zero curvature form geodesically complete surfaces, which means that allgeodesics( "straight lines" on the surface) may be extended indefinitely in either direction.

Zero curvature: An open strip with zero curvature may be constructed by gluing the opposite sides of a plane strip between two parallel lines, described above as the tautological linebundle.^[46]The resulting metric makes the open Möbius strip into a (geodesically) complete flat surface (i.e., having zero Gaussian curvature everywhere). This is the unique metric on the Möbius strip, up to uniform scaling, that is both flat and complete. It is thequotient spaceof a plane by aglide reflection,and (together with the plane,cylinder,torus,andKlein bottle) is one of only five two-dimensional completeflat manifolds.^[60]
Negative curvature: The open Möbius strip also admits complete metrics of constant negative curvature. One way to see this is to begin with theupper half plane (Poincaré) modelof thehyperbolic plane,a geometry of constant curvature whose lines are represented in the model by semicircles that meet the $x$ -axis at right angles. Take the subset of the upper half-plane between any two nested semicircles, and identify the outer semicircle with the left-right reversal of the inner semicircle. The result is topologically a complete and non-compact Möbius strip with constant negative curvature. It is a "nonstandard" complete hyperbolic surface in the sense that it contains a complete hyperbolichalf-plane(actually two, on opposite sides of the axis of glide-reflection), and is one of only 13 nonstandardsurfaces.^[61]Again, this can be understood as the quotient of the hyperbolic plane by a glidereflection.^[62]
Positive curvature: A Möbius strip of constant positive curvature cannot be complete, since it is known that the only complete surfaces of constant positive curvature are the sphere and theprojective plane.^[60]However, in a sense it is only one point away from being a complete surface, as the open Möbius strip is homeomorphic to theonce-puncturedprojective plane, the surface obtained by removing any one point from the projectiveplane.^[63]

Theminimal surfacesare described as having constant zeromean curvatureinstead of constant Gaussian curvature. The Sudanese Möbius strip was constructed as a minimal surface bounded by a great circle in a 3-sphere, but there is also a unique complete (boundaryless) minimal surface immersed in Euclidean space that has the topology of an open Möbius strip. It is called the Meeks Möbiusstrip,^[64]after its 1982 description byWilliam Hamilton Meeks, III.^[65]Although globally unstable as a minimal surface, small patches of it, bounded by non-contractible curves within the surface, can form stable embedded Möbius strips as minimalsurfaces.^[66]Both the Meeks Möbius strip, and every higher-dimensional minimal surface with the topology of the Möbius strip, can be constructed using solutions to theBjörling problem,which defines a minimal surface uniquely from its boundary curve and tangent planes along thiscurve.^[67]

Spaces of lines

The family of lines in the plane can be given the structure of a smooth space, with each line represented as a point in this space. The resulting space of lines istopologically equivalentto the open Möbiusstrip.^[68]One way to see this is to extend the Euclidean plane to thereal projective planeby adding one more line, theline at infinity.Byprojective dualitythe space of lines in the projective plane is equivalent to its space of points, the projective plane itself. Removing the line at infinity, to produce the space of Euclidean lines, punctures this space of projectivelines.^[69]Therefore, the space of Euclidean lines is a punctured projective plane, which is one of the forms of the open Möbiusstrip.^[63]The space of lines in thehyperbolic planecan be parameterized byunordered pairsof distinct points on a circle, the pairs of points at infinity of each line. This space, again, has the topology of an open Möbiusstrip.^[70]

These spaces of lines are highly symmetric. The symmetries of Euclidean lines include theaffine transformations,and the symmetries of hyperbolic lines include theMöbius transformations.^[71]The affine transformations and Möbius transformations both form6-dimensionalLie groups,topological spaces having a compatiblealgebraic structuredescribing the composition ofsymmetries.^[72]^[73]Because every line in the plane is symmetric to every other line, the open Möbius strip is ahomogeneous space,a space with symmetries that take every point to every other point. Homogeneous spaces of Lie groups are calledsolvmanifolds,and the Möbius strip can be used as acounterexample,showing that not every solvmanifold is anilmanifold,and that not every solvmanifold can be factored into adirect productof acompactsolvmanifoldwith $\mathbb {R} ^{n}$ .These symmetries also provide another way to construct the Möbius strip itself, as agroup modelof these Lie groups. A group model consists of a Lie group and astabilizer subgroupof its action; contracting thecosetsof the subgroup to points produces a space with the same topology as the underlying homogenous space. In the case of the symmetries of Euclidean lines, the stabilizer of the $x$ -axisconsists of all symmetries that take the axis to itself. Each line $\ell$ corresponds to a coset, the set of symmetries that map $\ell$ to the $x$ -axis.Therefore, thequotient space,a space that has one point per coset and inherits its topology from the space of symmetries, is the same as the space of lines, and is again an open Möbiusstrip.^[74]

Applications

Beyond the already-discussed applications of Möbius strips to the design of mechanical belts that wear evenly on their entire surface, and of the Plücker conoid to the design of gears, other applications of Möbius strips include:

Grapheneribbons twisted to form Möbius strips with new electronic characteristics including helical magnetism^[75]
Möbius aromaticity,a property oforganic chemicalswhose molecular structure forms a cycle, withmolecular orbitalsaligned along the cycle in the pattern of a Möbius strip^[76]^[77]
TheMöbius resistor,a strip of conductive material covering the single side of adielectricMöbius strip, in a way that cancels its ownself-inductance^[78]^[79]
Resonatorswith a compact design and a resonant frequency that is half that of identically constructed linear coils^[80]^[81]
Polarizationpatterns in light emerging from aq-plate^[82]
A proof of the impossibility of continuous, anonymous, and unanimous two-party aggregation rules insocial choice theory^[83]
Möbius loop roller coasters,a form of dual-tracked roller coaster in which the two tracks spiral around each other an odd number of times, so that the carriages return to the other track than the one they started on^[84]^[85]
World mapsprojected onto a Möbius strip with the convenient properties that there are no east–west boundaries, and that theantipodeof any point on the map can be found on the other printed side of the surface at the same point of the Möbius strip^[86]^[87]

Scientists have also studied the energetics ofsoap filmsshaped as Möbius strips,^[88]^[89]thechemical synthesisofmoleculeswith a Möbius strip shape,^[90]^[91]and the formation of largernanoscaleMöbius strips usingDNA origami.^[92]

In popular culture

Two-dimensional artworks featuring the Möbius strip include an untitled 1947 painting byCorrado Cagli(memorialized in a poem byCharles Olson),^[93]^[94]and two prints byM. C. Escher:Möbius Band I(1961), depicting three foldedflatfishbiting each others' tails; andMöbius Band II(1963), depicting ants crawling around alemniscate-shaped Möbius strip.^[95]^[96]It is also a popular subject ofmathematical sculpture,including works byMax Bill(Endless Ribbon,1953),José de Rivera(Infinity,1967), andSebastián.^[93]Atrefoil-knottedMöbius strip was used inJohn Robinson'sImmortality(1982).^[97]Charles O. Perry'sContinuum(1976) is one of several pieces by Perry exploring variations of the Möbius strip.^[98]

Recycling symbol

Google Drivelogo (2012–2014)

IMPAlogo on stamp

Because of their easily recognized form, Möbius strips are a common element ofgraphic design.^[97]The familiarthree-arrow logoforrecycling,designed in 1970, is based on the smooth triangular form of the Möbiusstrip,^[99]as was the logo for the environmentally-themedExpo '74.^[100]Some variations of the recycling symbol use a different embedding with three half-twists instead ofone,^[99]and the original version of theGoogle Drivelogo used a flat-folded three-twist Möbius strip, as have other similar designs.^[101]The BrazilianInstituto Nacional de Matemática Pura e Aplicada(IMPA) uses a stylized smooth Möbius strip as their logo, and has a matching large sculpture of a Möbius strip on display in their building.^[102]The Möbius strip has also featured in the artwork forpostage stampsfrom countries including Brazil, Belgium, the Netherlands, andSwitzerland.^[103]^[104]

Möbius strips have been a frequent inspiration for the architectural design of buildings and bridges. However, many of these are projects or conceptual designs rather than constructed objects, or stretch their interpretation of the Möbius strip beyond its recognizability as a mathematical form or a functional part of the architecture.^[105]^[106]An example is theNational Library of Kazakhstan,for which a building was planned in the shape of a thickened Möbius strip but refinished with a different design after the original architects pulled out of the project.^[107]One notable building incorporating a Möbius strip is theNASCAR Hall of Fame,which is surrounded by a large twisted ribbon of stainless steel acting as a façade and canopy, and evoking the curved shapes of racing tracks.^[108]On a smaller scale,Moebius Chair(2006) byPedro Reyesis acourting benchwhose base and sides have the form of a Möbius strip.^[109]As a form ofmathematics and fiber arts,scarveshave beenknitinto Möbius strips since the work ofElizabeth Zimmermannin the early 1980s.^[110]Infood styling,Möbius strips have been used for slicingbagels,^[111]making loops out ofbacon,^[112]and creating new shapes forpasta.^[113]

Although mathematically the Möbius strip and the fourth dimension are both purely spatial concepts, they have often been invoked inspeculative fictionas the basis for atime loopinto which unwary victims may become trapped. Examples of this trope includeMartin Gardner's "No-Sided Professor" (1946),Armin Joseph Deutsch's "A Subway Named Mobius"(1950) and the filmMoebius(1996) based on it. An entire world shaped like a Möbius strip is the setting ofArthur C. Clarke's "The Wall of Darkness" (1946), while conventional Möbius strips are used as clever inventions in multiple stories ofWilliam Hazlett Upsonfrom the 1940s.^[114]Other works of fiction have been analyzed as having a Möbius strip–like structure, in which elements of the plot repeat with a twist; these includeMarcel Proust'sIn Search of Lost Time(1913–1927),Luigi Pirandello'sSix Characters in Search of an Author(1921),Frank Capra'sIt's a Wonderful Life(1946),John Barth'sLost in the Funhouse(1968),Samuel R. Delany'sDhalgren(1975) and the filmDonnie Darko(2001).^[115]

One of themusical canonsbyJ. S. Bach,the fifth of 14 canons (BWV 1087) discovered in 1974 in Bach's copy of theGoldberg Variations,features aglide-reflectsymmetry in which each voice in the canon repeats, withinverted notes,the same motif from two measures earlier. Because of this symmetry, this canon can be thought of as having its score written on a Möbius strip.^[116]^[h]Inmusic theory,tones that differ by an octave are generally considered to be equivalent notes, and the space of possible notes forms a circle, thechromatic circle.Because the Möbius strip is theconfiguration spaceof two unordered points on a circle, the space of alltwo-note chordstakes the shape of a Möbius strip. This conception, and generalizations to more points, is a significantapplication of orbifolds to music theory.^[117]^[118]Modern musical groups taking their name from the Möbius strip include American electronic rock trioMobius Band^[119]and Norwegian progressive rock bandRing Van Möbius.^[120]

Möbius strips and their properties have been used in the design ofstage magic.One such trick, known as the Afghan bands, uses the fact that the Möbius strip remains a single strip when cut lengthwise. It originated in the 1880s, and was very popular in the first half of the twentieth century. Many versions of this trick exist and have been performed by famous illusionists such asHarry Blackstone Sr.andThomas Nelson Downs.^[121]^[122]

Notes

^PronouncedUS:/ˈmoʊbiəs,ˈmeɪ-/MOH-bee-əs,MAY-,UK:/ˈmɜːbiəs/;^[1]German:[ˈmøːbi̯ʊs].As is common for words containing anumlaut,it is also often spelledMobiusorMoebius.
^Essentially this example, but for aKlein bottlerather than a Möbius strip, is given byBlackett (1982).^[8]
^The length of a strip can be measured at its centerline, or by cutting the resulting Möbius strip perpendicularly to its boundary so that it forms a rectangle
^The flat-folded Möbius strip formed from three equilateral triangles does not come from anabstract simplicial complex,because all three triangles share the same three vertices, while abstract simplicial complexes require each triangle to have a different set of vertices.
^This piecewise planar and cylindrical embedding hassmoothnessclass $C^{2}$ ,and can be approximated arbitrarily accurately byinfinitely differentiable(class $C^{\infty }$ )embeddings.^[39]
^12/7 is the simplest rational number in the range of aspect ratios, between 1.695 and 1.73, for which the existence of a smooth embedding is unknown.
^These surfaces have smoothness class $C^{1}$ .For a more fine-grained analysis of the smoothness assumptions that force an embedding to be developable versus the assumptions under which theNash–Kuiper theoremallows arbitrarily flexible embeddings, see remarks byBartels & Hornung (2015),p. 116, following Theorem 2.2.^[39]
^Möbius strips have also been used to analyze many other canons by Bach and others, but in most of these cases other looping surfaces such as a cylinder could have been used equally well.^[116]

References

^Wells, John C.(2008).Longman Pronunciation Dictionary(3rd ed.). Longman.ISBN 978-1-4058-8118-0.
^Pickover, Clifford A.(2005).The Möbius Strip: Dr. August Möbius's Marvelous Band in Mathematics, Games, Literature, Art, Technology, and Cosmology.Thunder's Mouth Press. pp. 28–29.ISBN 978-1-56025-826-1.
^^a ^b ^c ^dLarison, Lorraine L. (1973). "The Möbius band in Roman mosaics".American Scientist.61(5): 544–547.Bibcode:1973AmSci..61..544L.JSTOR 27843983.
^^a ^b ^cCartwright, Julyan H. E.;González, Diego L. (2016). "Möbius strips before Möbius: topological hints in ancient representations".The Mathematical Intelligencer.38(2): 69–76.arXiv:1609.07779.Bibcode:2016arXiv160907779C.doi:10.1007/s00283-016-9631-8.MR 3507121.S2CID 119587191.
^Flapan, Erica(2000).When Topology Meets Chemistry: A Topological Look at Molecular Chirality.Outlooks. Washington, DC: Mathematical Association of America. pp.82–83.doi:10.1017/CBO9780511626272.ISBN 0-521-66254-0.MR 1781912.
^^a ^b ^cPickover (2005),pp. 8–9.
^Woll, John W. Jr. (Spring 1971). "One-sided surfaces and orientability".The Two-Year College Mathematics Journal.2(1): 5–18.doi:10.2307/3026946.JSTOR 3026946.
^Blackett, Donald W. (1982).Elementary Topology: A Combinatorial and Algebraic Approach.Academic Press. p. 195.ISBN 9781483262536.
^Frolkina, Olga D. (2018). "Pairwise disjoint Moebius bands in space".Journal of Knot Theory and Its Ramifications.27(9): 1842005, 9.arXiv:2212.02983.doi:10.1142/S0218216518420051.MR 3848635.S2CID 126421578.
^Lamb, Evelyn (February 20, 2019)."Möbius strips defy a link with infinity".Quanta Magazine.
^Melikhov, Sergey A. (2019). "A note on O. Frolkina's paper" Pairwise disjoint Moebius bands in space "".Journal of Knot Theory and Its Ramifications.28(7): 1971001, 3.arXiv:1810.04089.doi:10.1142/s0218216519710019.MR 3975576.S2CID 119179202.
^Pickover (2005),p. 52.
^Pickover (2005),p. 12.
^Kyle, R. H. (1955). "Embeddings of Möbius bands in 3-dimensional space".Proceedings of the Royal Irish Academy, Section A.57:131–136.JSTOR 20488581.MR 0091480.
^Pickover (2005),p. 11.
^Massey, William S. (1991).A Basic Course in Algebraic Topology.Graduate Texts in Mathematics. Vol. 127. New York: Springer-Verlag. p. 49.ISBN 0-387-97430-X.MR 1095046.
^Rouse Ball, W. W.(1892). "Paradromic rings".Mathematical Recreations and Problems of Past and Present Times(2nd ed.). London & New York: Macmillan and co. pp. 53–54.ISBN 9780608377803.
^Bennett, G. T.(June 1923)."Paradromic rings".Nature.111(2800): 882.Bibcode:1923Natur.111R.882B.doi:10.1038/111882b0.S2CID 4099647.
^^a ^bTietze, Heinrich(1910)."Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen"(PDF).Jahresbericht der Deutschen Mathematiker-Vereinigung.19:155–159.
^Ringel, G.;Youngs, J. W. T. (1968)."Solution of the Heawood map-coloring problem".Proceedings of the National Academy of Sciences of the United States of America.60(2): 438–445.Bibcode:1968PNAS...60..438R.doi:10.1073/pnas.60.2.438.MR 0228378.PMC225066.PMID 16591648.
^Jablan, Slavik; Radović, Ljiljana; Sazdanović, Radmila (2011). "Nonplanar graphs derived from Gauss codes of virtual knots and links".Journal of Mathematical Chemistry.49(10): 2250–2267.doi:10.1007/s10910-011-9884-6.MR 2846715.S2CID 121332704.
^Larsen, Mogens Esrom (1994). "Misunderstanding my mazy mazes may make me miserable". InGuy, Richard K.;Woodrow, Robert E. (eds.).Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History held at the University of Calgary, Calgary, Alberta, August 1986.MAA Spectrum. Washington, DC: Mathematical Association of America. pp. 289–293.ISBN 0-88385-516-X.MR 1303141..SeeFigure 7, p. 292.
^Maschke, Heinrich(1900)."Note on the unilateral surface of Moebius".Transactions of the American Mathematical Society.1(1): 39.doi:10.2307/1986401.JSTOR 1986401.MR 1500522.
^Junghenn, Hugo D. (2015).A Course in Real Analysis.Boca Raton, Florida: CRC Press. p. 430.ISBN 978-1-4822-1927-2.MR 3309241.
^Séquin, Carlo H.(2005)."Splitting tori, knots, and Moebius bands".In Sarhangi, Reza; Moody, Robert V. (eds.).Renaissance Banff: Mathematics, Music, Art, Culture.Southwestern College, Winfield, Kansas: Bridges Conference. pp. 211–218.ISBN 0-9665201-6-5.
^^a ^bFrancis, George K. (1987). "Plücker conoid".A Topological Picturebook.Springer-Verlag, New York. pp. 81–83.ISBN 0-387-96426-6.MR 0880519.
^Dooner, David B.; Seireg, Ali (1995)."3.4.2 The cylindroid".The Kinematic Geometry of Gearing: A Concurrent Engineering Approach.Wiley Series in Design Engineering. Vol. 3. John Wiley & Sons. pp. 135–137.ISBN 9780471045977.
^^a ^bBarr, Stephen (1964).Experiments in Topology.New York: Thomas Y. Crowell Company. pp. 40–49, 200–201.ISBN 9780690278620.
^^a ^b ^c ^d ^eFuchs, Dmitry;Tabachnikov, Serge(2007). "Lecture 14: Paper Möbius band".Mathematical Omnibus: Thirty Lectures on Classic Mathematics(PDF).Providence, Rhode Island: American Mathematical Society. pp. 199–206.doi:10.1090/mbk/046.ISBN 978-0-8218-4316-1.MR 2350979.Archived fromthe original(PDF)on 2016-04-24.
^Pook, Les (2003)."4.2: The trihexaflexagon revisited".Flexagons Inside Out.Cambridge, UK: Cambridge University Press. pp. 33–36.doi:10.1017/CBO9780511543302.ISBN 0-521-81970-9.MR 2008500.
^^a ^bKühnel, W.;Banchoff, T. F.(1983)."The 9-vertex complex projective plane"(PDF).The Mathematical Intelligencer.5(3): 11–22.doi:10.1007/BF03026567.MR 0737686.S2CID 120926324.
^Kuiper, Nicolaas H.(1972)."Tight topological embeddings of the Moebius band".Journal of Differential Geometry.6(3): 271–283.doi:10.4310/jdg/1214430493.MR 0314057.
^Szilassi, Lajos(2008)."A polyhedral model in Euclidean 3-space of the six-pentagon map of the projective plane".Discrete & Computational Geometry.40(3): 395–400.doi:10.1007/s00454-007-9033-y.MR 2443291.S2CID 38606607.
^Tuckerman, Bryant(1948). "A non-singular polyhedral Möbius band whose boundary is a triangle".American Mathematical Monthly.55(5): 309–311.doi:10.2307/2305482.JSTOR 2305482.MR 0024138.
^Bonnington, C. Paul; Nakamoto, Atsuhiro (2008)."Geometric realization of a triangulation on the projective plane with one face removed".Discrete & Computational Geometry.40(1): 141–157.doi:10.1007/s00454-007-9035-9.MR 2429652.S2CID 10887519.
^Brehm, Ulrich (1983). "A nonpolyhedral triangulated Möbius strip".Proceedings of the American Mathematical Society.89(3): 519–522.doi:10.2307/2045508.JSTOR 2045508.MR 0715878.
^Nakamoto, Atsuhiro; Tsuchiya, Shoichi (2012)."On geometrically realizable Möbius triangulations".Discrete Mathematics.312(14): 2135–2139.doi:10.1016/j.disc.2011.06.007.MR 2921579.
^^a ^bHinz, Denis F.; Fried, Eliot (2015). "Translation of Michael Sadowsky's paper" An elementary proof for the existence of a developable Möbius band and the attribution of the geometric problem to a variational problem "".Journal of Elasticity.119(1–2): 3–6.arXiv:1408.3034.doi:10.1007/s10659-014-9490-5.MR 3326180.S2CID 119733903.Reprinted inFosdick, Roger; Fried, Eliot (2016).The Mechanics of Ribbons and Möbius Bands(PDF).Springer, Dordrecht. pp. 3–6.doi:10.1007/978-94-017-7300-3.ISBN 978-94-017-7299-0.MR 3381564.
^^a ^b ^c ^dBartels, Sören; Hornung, Peter (2015). "Bending paper and the Möbius strip".Journal of Elasticity.119(1–2): 113–136.doi:10.1007/s10659-014-9501-6.MR 3326187.S2CID 119782792.Reprinted inFosdick & Fried (2016),pp. 113–136. See in particular Section 5.2, pp. 129–130.
^^a ^bStarostin, E. L.; van der Heijden, G. H. M. (2015)."Equilibrium shapes with stress localisation for inextensible elastic Möbius and other strips".Journal of Elasticity.119(1–2): 67–112.doi:10.1007/s10659-014-9495-0.MR 3326186.S2CID 53462568.Reprinted inFosdick & Fried (2016),pp. 67–112.
^Schwarz, Gideon E. (1990). "The dark side of the Moebius strip".The American Mathematical Monthly.97(10): 890–897.doi:10.1080/00029890.1990.11995680.JSTOR 2324325.MR 1079975.
^^a ^bHalpern, B.; Weaver, C. (1977)."Inverting a cylinder through isometric immersions and isometric embeddings".Transactions of the American Mathematical Society.230:41–70.doi:10.2307/1997711.JSTOR 1997711.MR 0474388.
^^a ^bSchwartz, Richard Evan(2021). "An improved bound on the optimal paper Moebius band".Geometriae Dedicata.215:255–267.arXiv:2008.11610.doi:10.1007/s10711-021-00648-5.MR 4330341.S2CID 220279013.
^Schwartz, Richard(2023). "The optimal paper Moebius band".arXiv:2308.12641[math.MG].
^Crowell, Rachel (September 12, 2023)."Mathematicians solve 50-year-old Möbius strip puzzle".Scientific American.
^^a ^bDundas, Bjørn Ian (2018). "Example 5.1.3: The unbounded Möbius band".A Short Course in Differential Topology.Cambridge Mathematical Textbooks. Cambridge University Press, Cambridge. p.https://books.google.com/books?id=7a1eDwAAQBAJ&pg=PA101.doi:10.1017/9781108349130.ISBN 978-1-108-42579-7.MR 3793640.S2CID 125997451.
^Blanuša, Danilo(1954). "Le plongement isométrique de la bande de Möbius infiniment large euclidienne dans un espace sphérique, parabolique ou hyperbolique à quatre dimensions".Bulletin International de l'Académie Yougoslave des Sciences et des Beaux-Arts.12:19–23.MR 0071060.
^Wunderlich, W. (1962). "Über ein abwickelbares Möbiusband".Monatshefte für Mathematik.66(3): 276–289.doi:10.1007/BF01299052.MR 0143115.S2CID 122215321.
^Schwarz, Gideon (1990)."A pretender to the title 'canonical Moebius strip'".Pacific Journal of Mathematics.143(1): 195–200.doi:10.2140/pjm.1990.143.195.MR 1047406.
^Hilbert, David;Cohn-Vossen, Stephan (1952).Geometry and the Imagination(2nd ed.). Chelsea. pp. 315–316.ISBN 978-0-8284-1087-8.
^Spivak, Michael(1979).A Comprehensive Introduction to Differential Geometry, Volume I(2nd ed.). Wilmington, Delaware: Publish or Perish. p. 591.
^^a ^b ^cKnöppel, Felix (Summer 2019)."Tutorial 3: Lawson's Minimal Surfaces and the Sudanese Möbius Band".DDG2019: Visualization course at TU Berlin.
^^a ^bLawson, H. Blaine Jr.(1970). "Complete minimal surfaces in $S^{3}$ ".Annals of Mathematics.Second Series.92(3): 335–374.doi:10.2307/1970625.JSTOR 1970625.MR 0270280.See Section 7, pp. 350–353, where the Klein bottle is denoted $\tau _{1,2}$ .
^^a ^bSchleimer, Saul; Segerman, Henry (2012)."Sculptures in $S 3$ ".In Bosch, Robert; McKenna, Douglas; Sarhangi, Reza (eds.).Proceedings of Bridges 2012: Mathematics, Music, Art, Architecture, Culture.Phoenix, Arizona: Tessellations Publishing. pp. 103–110.arXiv:1204.4952.ISBN 978-1-938664-00-7.
^Gunn, Charles (August 23, 2018)."Sudanese Möbius Band".Vimeo.Retrieved2022-03-17.
^Franzoni, Gregorio (2012)."The Klein bottle: variations on a theme".Notices of the American Mathematical Society.59(8): 1076–1082.doi:10.1090/noti880.MR 2985809.
^Huggett, Stephen; Jordan, David (2009).A Topological Aperitif(Revised ed.). Springer-Verlag. p. 57.ISBN 978-1-84800-912-7.MR 2483686.
^Flapan, Erica(2016).Knots, Molecules, and the Universe: An Introduction to Topology.Providence, Rhode Island: American Mathematical Society. pp. 99–100.doi:10.1090/mbk/096.ISBN 978-1-4704-2535-7.MR 3443369.
^Richeson, David S.(2008).Euler's Gem: The Polyhedron Formula and the Birth of Topology.Princeton, New Jersey: Princeton University Press. p.171.ISBN 978-0-691-12677-7.MR 2440945.
^^a ^bGodinho, Leonor; Natário, José (2014).An Introduction to Riemannian Geometry: With Applications to Mechanics and Relativity.Universitext. Springer, Cham. pp. 152–153.doi:10.1007/978-3-319-08666-8.ISBN 978-3-319-08665-1.MR 3289090.
^Cantwell, John; Conlon, Lawrence (2015). "Hyperbolic geometry and homotopic homeomorphisms of surfaces".Geometriae Dedicata.177:27–42.arXiv:1305.1379.doi:10.1007/s10711-014-9975-1.MR 3370020.S2CID 119640200.
^Stillwell, John(1992). "4.6 Classification of isometries".Geometry of Surfaces.Universitext. Cham: Springer. pp. 96–98.doi:10.1007/978-1-4612-0929-4.ISBN 0-387-97743-0.MR 1171453.
^^a ^bSeifert, Herbert;Threlfall, William(1980).A Textbook of Topology.Pure and Applied Mathematics. Vol. 89. Translated by Goldman, Michael A. New York & London: Academic Press. p. 12.ISBN 0-12-634850-2.MR 0575168.
^López, Francisco J.; Martín, Francisco (1997). "Complete nonorientable minimal surfaces with the highest symmetry group".American Journal of Mathematics.119(1): 55–81.doi:10.1353/ajm.1997.0004.MR 1428058.S2CID 121366986.
^Meeks, William H. III(1981). "The classification of complete minimal surfaces in $\mathbb {R} ^{3}$ with total curvature greater than $-8\pi$ ".Duke Mathematical Journal.48(3): 523–535.doi:10.1215/S0012-7094-81-04829-8.MR 0630583.
^Pesci, Adriana I.;Goldstein, Raymond E.;Alexander, Gareth P.;Moffatt, H. Keith(2015)."Instability of a Möbius strip minimal surface and a link with systolic geometry"(PDF).Physical Review Letters.114(12): 127801.Bibcode:2015PhRvL.114l7801P.doi:10.1103/PhysRevLett.114.127801.MR 3447638.PMID 25860771.
^Mira, Pablo (2006). "Complete minimal Möbius strips in $\mathbb {R} ^{n}$ and the Björling problem ".Journal of Geometry and Physics.56(9): 1506–1515.Bibcode:2006JGP....56.1506M.doi:10.1016/j.geomphys.2005.08.001.MR 2240407.
^Parker, Phillip E. (1993)."Spaces of geodesics".In Del Riego, L. (ed.).Differential Geometry Workshop on Spaces of Geometry (Guanajuato, 1992).Aportaciones Mat. Notas Investigación. Vol. 8. Soc. Mat. Mexicana, México. pp. 67–79.MR 1304924.Archived from the original on 2016-03-13.Retrieved2022-03-21.{{cite book}}:CS1 maint: bot: original URL status unknown (link)
^Bickel, Holger (1999). "Duality in stable planes and related closure and kernel operations".Journal of Geometry.64(1–2): 8–15.doi:10.1007/BF01229209.MR 1675956.S2CID 122209943.
^Mangahas, Johanna (July 2017). "Office Hour Five: The Ping-Pong Lemma". In Clay, Matt; Margalit, Dan (eds.).Office Hours with a Geometric Group Theorist.Princeton University Press. pp. 85–105.doi:10.1515/9781400885398.ISBN 9781400885398.See in particular Project 7, pp. 104–105.
^Ramírez Galarza, Ana Irene; Seade, José (2007).Introduction to Classical Geometries.Basel: Birkhäuser Verlag. pp. 83–88, 157–163.ISBN 978-3-7643-7517-1.MR 2305055.
^Fomenko, Anatolij T.;Kunii, Tosiyasu L. (2013).Topological Modeling for Visualization.Springer. p. 269.ISBN 9784431669562.
^Isham, Chris J. (1999).Modern Differential Geometry for Physicists.World Scientific lecture notes in physics. Vol. 61 (2nd ed.). World Scientific. p. 269.ISBN 981-02-3555-0.MR 1698234.
^Gorbatsevich, V. V.; Onishchik, A. L.; Vinberg, È. B. (1993).Lie groups and Lie algebras I: Foundations of Lie Theory; Lie Transformation Groups.Encyclopaedia of Mathematical Sciences. Vol. 20. Springer-Verlag, Berlin. pp. 164–166.doi:10.1007/978-3-642-57999-8.ISBN 3-540-18697-2.MR 1306737.
^Yamashiro, Atsushi; Shimoi, Yukihiro; Harigaya, Kikuo; Wakabayashi, Katsunori (2004). "Novel electronic states in graphene ribbons: competing spin and charge orders".Physica E.22(1–3): 688–691.arXiv:cond-mat/0309636.Bibcode:2004PhyE...22..688Y.doi:10.1016/j.physe.2003.12.100.S2CID 17102453.
^Rzepa, Henry S. (September 2005). "Möbius aromaticity and delocalization".Chemical Reviews.105(10): 3697–3715.doi:10.1021/cr030092l.PMID 16218564.
^Yoon, Zin Seok; Osuka, Atsuhiro; Kim, Dongho (May 2009). "Möbius aromaticity and antiaromaticity in expanded porphyrins".Nature Chemistry.1(2): 113–122.Bibcode:2009NatCh...1..113Y.doi:10.1038/nchem.172.PMID 21378823.
^"Making resistors with math".Time.Vol. 84, no. 13. September 25, 1964.
^Pickover (2005),pp. 45–46.
^Pond, J. M. (2000). "Mobius dual-mode resonators and bandpass filters".IEEE Transactions on Microwave Theory and Techniques.48(12): 2465–2471.Bibcode:2000ITMTT..48.2465P.doi:10.1109/22.898999.
^Rohde, Ulrich L.; Poddar, Ajay; Sundararajan, D. (November 2013)."Printed resonators: Möbius strip theory and applications"(PDF).Microwave Journal.56(11).
^Bauer, Thomas; Banzer, Peter; Karimi, Ebrahim; Orlov, Sergej; Rubano, Andrea; Marrucci, Lorenzo; Santamato, Enrico; Boyd, Robert W.; Leuchs, Gerd (February 2015). "Observation of optical polarization Möbius strips".Science.347(6225): 964–966.Bibcode:2015Sci...347..964B.doi:10.1126/science.1260635.PMID 25636796.S2CID 206562350.
^Candeal, Juan Carlos; Induráin, Esteban (January 1994). "The Moebius strip and a social choice paradox".Economics Letters.45(3): 407–412.doi:10.1016/0165-1765(94)90045-0.
^Easdown, Martin (2012).Amusement Park Rides.Bloomsbury Publishing. p. 43.ISBN 9781782001522.
^Hook, Patrick (2019).Ticket To Ride: The Essential Guide to the World's Greatest Roller Coasters and Thrill Rides.Chartwell Books. p. 20.ISBN 9780785835776.
^Tobler, Waldo R.(1961)."A world map on a Möbius strip".Surveying & Mapping.21:486.
^Kumler, Mark P.;Tobler, Waldo R. (January 1991). "Three world maps on a Moebius strip".Cartography and Geographic Information Systems.18(4): 275–276.doi:10.1559/152304091783786781.
^Courant, Richard(1940). "Soap film experiments with minimal surfaces".The American Mathematical Monthly.47(3): 167–174.doi:10.1080/00029890.1940.11990957.JSTOR 2304225.MR 0001622.
^Goldstein, Raymond E.;Moffatt, H. Keith;Pesci, Adriana I.;Ricca, Renzo L.(December 2010)."Soap-film Möbius strip changes topology with a twist singularity".Proceedings of the National Academy of Sciences.107(51): 21979–21984.Bibcode:2010PNAS..10721979G.doi:10.1073/pnas.1015997107.PMC3009808.
^Walba, David M.; Richards, Rodney M.; Haltiwanger, R. Curtis (June 1982). "Total synthesis of the first molecular Moebius strip".Journal of the American Chemical Society.104(11): 3219–3221.doi:10.1021/ja00375a051.
^Pickover (2005),pp. 52–58.
^Gitig, Diana (October 18, 2010)."Chemical origami used to create a DNA Möbius strip".Ars Technica.Retrieved2022-03-28.
^^a ^bEmmer, Michele (Spring 1980)."Visual art and mathematics: the Moebius band".Leonardo.13(2): 108–111.doi:10.2307/1577979.JSTOR 1577979.S2CID 123908555.
^Byers, Mark (2018).Charles Olson and American Modernism: The Practice of the Self.Oxford University Press. pp. 77–78.ISBN 9780198813255.
^Crato, Nuno (2010). "Escher and the Möbius strip".Figuring It Out: Entertaining Encounters with Everyday Math.Springer. pp. 123–126.doi:10.1007/978-3-642-04833-3_29.
^Kersten, Erik (March 13, 2017)."Möbius Strip I".Escher in the Palace.Retrieved2022-04-17.
^^a ^bPickover (2005),p. 13.
^Brecher, Kenneth (2017)."Art of infinity".In Swart, David; Séquin, Carlo H.; Fenyvesi, Kristóf (eds.).Proceedings of Bridges 2017: Mathematics, Art, Music, Architecture, Education, Culture.Phoenix, Arizona: Tessellations Publishing. pp. 153–158.ISBN 978-1-938664-22-9.
^^a ^bPeterson, Ivars(2002)."Recycling topology".Mathematical Treks: From Surreal Numbers to Magic Circles.MAA Spectrum. Mathematical Association of America, Washington, DC. pp. 31–35.ISBN 0-88385-537-2.MR 1874198.
^"Expo '74 symbol selected".The Spokesman-Review.March 12, 1972. p. 1.
^Millward, Steven (April 30, 2012)."Did Google Drive Copy its Icon From a Chinese App?".Tech in Asia.Retrieved2022-03-27– via Yahoo! News.
^"Símbolo do IMPA".Para quem é fã do IMPA, dez curiosidades sobre o instituto.IMPA. May 7, 2020.Retrieved2022-03-27.
^Pickover (2005),pp. 156–157.
^Decker, Heinz; Stark, Eberhard (1983). "Möbius-Bänder:...und natürlich auch auf Briefmarken".Praxis der Mathematik.25(7): 207–215.MR 0720681.
^Thulaseedas, Jolly; Krawczyk, Robert J. (2003)."Möbius concepts in architecture".In Barrallo, Javier; Friedman, Nathaniel; Maldonado, Juan Antonio; Mart\'\inez-Aroza, José; Sarhangi, Reza; Séquin, Carlo (eds.).Meeting Alhambra, ISAMA-BRIDGES Conference Proceedings.Granada, Spain: University of Granada. pp. 353–360.ISBN 84-930669-1-5.
^Séquin, Carlo H.(January 2018). "Möbius bridges".Journal of Mathematics and the Arts.12(2–3): 181–194.doi:10.1080/17513472.2017.1419331.S2CID 216116708.
^Wainwright, Oliver (October 17, 2017)."'Norman said the president wants a pyramid': how starchitects built Astana ".The Guardian.
^Muret, Don (May 17, 2010)."NASCAR Hall of Fame 'looks fast sitting still'".Sports Business Journal.
^Gopnik, Blake (October 17, 2014)."Pedro Reyes Makes an Infinite Love Seat".Artnet News.
^Thomas, Nancy J. (October 4, 1998)."Making a Mobius a matter of mathematics".The Times (Trenton).p. aa3 – viaNewsBank.
^Pashman, Dan (August 6, 2015)."Cut Your Bagel The Mathematically Correct Way".The Salt.NPR.
^Miller, Ross (September 5, 2014)."How to make a mathematically-endless strip of bacon".The Verge.
^Chang, Kenneth (January 9, 2012)."Pasta Graduates From Alphabet Soup to Advanced Geometry".The New York Times.
^Pickover (2005),pp. 174–177.
^Pickover (2005),pp. 179–187.
^^a ^bPhillips, Tony (November 25, 2016)."Bach and the musical Möbius strip".Plus Magazine.Reprinted from an American Mathematical Society Feature Column.
^Moskowitz, Clara(May 6, 2008)."Music reduced to beautiful math".Live Science.Retrieved2022-03-21.
^Tymoczko, Dmitri(July 7, 2006)."The geometry of musical chords"(PDF).Science.313(5783): 72–4.Bibcode:2006Sci...313...72T.doi:10.1126/science.1126287.JSTOR 3846592.PMID 16825563.S2CID 2877171.
^Parks, Andrew (August 30, 2007)."Mobius Band: Friendly Fire".Magnet.
^Lawson, Dom (February 9, 2021)."Ring Van Möbius".Prog.
^Prevos, Peter (2018).The Möbius Strip in Magic: A Treatise on the Afghan Bands.Kangaroo Flat: Third Hemisphere.
^Gardner, Martin(1956)."The Afghan Bands".Mathematics, Magic and Mystery.New York: Dover Books. pp. 70–73.

External links

Media related toMoebius Stripat Wikimedia Commons
Weisstein, Eric W."Möbius Strip".MathWorld.

[2] PronouncedUS:/ˈmoʊbiəs,ˈmeɪ-/MOH-bee-əs,MAY-,UK:/ˈmɜːbiəs/;^[1]German:[ˈmøːbi̯ʊs].As is common for words containing anumlaut,it is also often spelledMobiusorMoebius.

[10] Essentially this example, but for aKlein bottlerather than a Möbius strip, is given byBlackett (1982).^[8]

[30] The length of a strip can be measured at its centerline, or by cutting the resulting Möbius strip perpendicularly to its boundary so that it forms a rectangle

[35] The flat-folded Möbius strip formed from three equilateral triangles does not come from anabstract simplicial complex,because all three triangles share the same three vertices, while abstract simplicial complexes require each triangle to have a different set of vertices.

[44] This piecewise planar and cylindrical embedding hassmoothnessclass $C^{2}$ ,and can be approximated arbitrarily accurately byinfinitely differentiable(class $C^{\infty }$ )embeddings.^[39]

[49] 12/7 is the simplest rational number in the range of aspect ratios, between 1.695 and 1.73, for which the existence of a smooth embedding is unknown.

[52] These surfaces have smoothness class $C^{1}$ .For a more fine-grained analysis of the smoothness assumptions that force an embedding to be developable versus the assumptions under which theNash–Kuiper theoremallows arbitrarily flexible embeddings, see remarks byBartels & Hornung (2015),p. 116, following Theorem 2.2.^[39]

[124] Möbius strips have also been used to analyze many other canons by Bach and others, but in most of these cases other looping surfaces such as a cylinder could have been used equally well.^[116]

[1] Wells, John C.(2008).Longman Pronunciation Dictionary(3rd ed.). Longman.ISBN 978-1-4058-8118-0.

[pickover-3] Pickover, Clifford A.(2005).The Möbius Strip: Dr. August Möbius's Marvelous Band in Mathematics, Games, Literature, Art, Technology, and Cosmology.Thunder's Mouth Press. pp. 28–29.ISBN 978-1-56025-826-1.

[roman-4] Larison, Lorraine L. (1973). "The Möbius band in Roman mosaics".American Scientist.61(5): 544–547.Bibcode:1973AmSci..61..544L.JSTOR 27843983.

[ancient-5] Cartwright, Julyan H. E.;González, Diego L. (2016). "Möbius strips before Möbius: topological hints in ancient representations".The Mathematical Intelligencer.38(2): 69–76.arXiv:1609.07779.Bibcode:2016arXiv160907779C.doi:10.1007/s00283-016-9631-8.MR 3507121.S2CID 119587191.

[chirality-6] Flapan, Erica(2000).When Topology Meets Chemistry: A Topological Look at Molecular Chirality.Outlooks. Washington, DC: Mathematical Association of America. pp.82–83.doi:10.1017/CBO9780511626272.ISBN 0-521-66254-0.MR 1781912.

[FOOTNOTEPickover20058–9-7] Pickover (2005),pp. 8–9.

[woll-8] Woll, John W. Jr. (Spring 1971). "One-sided surfaces and orientability".The Two-Year College Mathematics Journal.2(1): 5–18.doi:10.2307/3026946.JSTOR 3026946.

[blackett-9] Blackett, Donald W. (1982).Elementary Topology: A Combinatorial and Algebraic Approach.Academic Press. p. 195.ISBN 9781483262536.

[frolkina-11] Frolkina, Olga D. (2018). "Pairwise disjoint Moebius bands in space".Journal of Knot Theory and Its Ramifications.27(9): 1842005, 9.arXiv:2212.02983.doi:10.1142/S0218216518420051.MR 3848635.S2CID 126421578.

[defy-12] Lamb, Evelyn (February 20, 2019)."Möbius strips defy a link with infinity".Quanta Magazine.

[melikhov-13] Melikhov, Sergey A. (2019). "A note on O. Frolkina's paper" Pairwise disjoint Moebius bands in space "".Journal of Knot Theory and Its Ramifications.28(7): 1971001, 3.arXiv:1810.04089.doi:10.1142/s0218216519710019.MR 3975576.S2CID 119179202.

[FOOTNOTEPickover200552-14] Pickover (2005),p. 52.

[FOOTNOTEPickover200512-15] Pickover (2005),p. 12.

[kyle-16] Kyle, R. H. (1955). "Embeddings of Möbius bands in 3-dimensional space".Proceedings of the Royal Irish Academy, Section A.57:131–136.JSTOR 20488581.MR 0091480.

[FOOTNOTEPickover200511-17] Pickover (2005),p. 11.

[massey-18] Massey, William S. (1991).A Basic Course in Algebraic Topology.Graduate Texts in Mathematics. Vol. 127. New York: Springer-Verlag. p. 49.ISBN 0-387-97430-X.MR 1095046.

[rouseball-19] Rouse Ball, W. W.(1892). "Paradromic rings".Mathematical Recreations and Problems of Past and Present Times(2nd ed.). London & New York: Macmillan and co. pp. 53–54.ISBN 9780608377803.

[paradromic-20] Bennett, G. T.(June 1923)."Paradromic rings".Nature.111(2800): 882.Bibcode:1923Natur.111R.882B.doi:10.1038/111882b0.S2CID 4099647.

[tietze-21] Tietze, Heinrich(1910)."Einige Bemerkungen zum Problem des Kartenfärbens auf einseitigen Flächen"(PDF).Jahresbericht der Deutschen Mathematiker-Vereinigung.19:155–159.

[ringel-youngs-22] Ringel, G.;Youngs, J. W. T. (1968)."Solution of the Heawood map-coloring problem".Proceedings of the National Academy of Sciences of the United States of America.60(2): 438–445.Bibcode:1968PNAS...60..438R.doi:10.1073/pnas.60.2.438.MR 0228378.PMC225066.PMID 16591648.

[jab-rad-saz-23] Jablan, Slavik; Radović, Ljiljana; Sazdanović, Radmila (2011). "Nonplanar graphs derived from Gauss codes of virtual knots and links".Journal of Mathematical Chemistry.49(10): 2250–2267.doi:10.1007/s10910-011-9884-6.MR 2846715.S2CID 121332704.

[larsen-24] Larsen, Mogens Esrom (1994). "Misunderstanding my mazy mazes may make me miserable". InGuy, Richard K.;Woodrow, Robert E. (eds.).Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History held at the University of Calgary, Calgary, Alberta, August 1986.MAA Spectrum. Washington, DC: Mathematical Association of America. pp. 289–293.ISBN 0-88385-516-X.MR 1303141..SeeFigure 7, p. 292.

[maschke-25] Maschke, Heinrich(1900)."Note on the unilateral surface of Moebius".Transactions of the American Mathematical Society.1(1): 39.doi:10.2307/1986401.JSTOR 1986401.MR 1500522.

[parameterization-26] Junghenn, Hugo D. (2015).A Course in Real Analysis.Boca Raton, Florida: CRC Press. p. 430.ISBN 978-1-4822-1927-2.MR 3309241.

[split-tori-27] Séquin, Carlo H.(2005)."Splitting tori, knots, and Moebius bands".In Sarhangi, Reza; Moody, Robert V. (eds.).Renaissance Banff: Mathematics, Music, Art, Culture.Southwestern College, Winfield, Kansas: Bridges Conference. pp. 211–218.ISBN 0-9665201-6-5.

[francis-28] Francis, George K. (1987). "Plücker conoid".A Topological Picturebook.Springer-Verlag, New York. pp. 81–83.ISBN 0-387-96426-6.MR 0880519.

[dooner-seirig-29] Dooner, David B.; Seireg, Ali (1995)."3.4.2 The cylindroid".The Kinematic Geometry of Gearing: A Concurrent Engineering Approach.Wiley Series in Design Engineering. Vol. 3. John Wiley & Sons. pp. 135–137.ISBN 9780471045977.

[barr-31] Barr, Stephen (1964).Experiments in Topology.New York: Thomas Y. Crowell Company. pp. 40–49, 200–201.ISBN 9780690278620.

[fuchs-tabachnikov-32] Fuchs, Dmitry;Tabachnikov, Serge(2007). "Lecture 14: Paper Möbius band".Mathematical Omnibus: Thirty Lectures on Classic Mathematics(PDF).Providence, Rhode Island: American Mathematical Society. pp. 199–206.doi:10.1090/mbk/046.ISBN 978-0-8218-4316-1.MR 2350979.Archived fromthe original(PDF)on 2016-04-24.

[pook-33] Pook, Les (2003)."4.2: The trihexaflexagon revisited".Flexagons Inside Out.Cambridge, UK: Cambridge University Press. pp. 33–36.doi:10.1017/CBO9780511543302.ISBN 0-521-81970-9.MR 2008500.

[9vertex-34] Kühnel, W.;Banchoff, T. F.(1983)."The 9-vertex complex projective plane"(PDF).The Mathematical Intelligencer.5(3): 11–22.doi:10.1007/BF03026567.MR 0737686.S2CID 120926324.

[kuiper-36] Kuiper, Nicolaas H.(1972)."Tight topological embeddings of the Moebius band".Journal of Differential Geometry.6(3): 271–283.doi:10.4310/jdg/1214430493.MR 0314057.

[szilassi-37] Szilassi, Lajos(2008)."A polyhedral model in Euclidean 3-space of the six-pentagon map of the projective plane".Discrete & Computational Geometry.40(3): 395–400.doi:10.1007/s00454-007-9033-y.MR 2443291.S2CID 38606607.

[tuckerman-38] Tuckerman, Bryant(1948). "A non-singular polyhedral Möbius band whose boundary is a triangle".American Mathematical Monthly.55(5): 309–311.doi:10.2307/2305482.JSTOR 2305482.MR 0024138.

[bon-nak-39] Bonnington, C. Paul; Nakamoto, Atsuhiro (2008)."Geometric realization of a triangulation on the projective plane with one face removed".Discrete & Computational Geometry.40(1): 141–157.doi:10.1007/s00454-007-9035-9.MR 2429652.S2CID 10887519.

[brehm-40] Brehm, Ulrich (1983). "A nonpolyhedral triangulated Möbius strip".Proceedings of the American Mathematical Society.89(3): 519–522.doi:10.2307/2045508.JSTOR 2045508.MR 0715878.

[nak-tsu-41] Nakamoto, Atsuhiro; Tsuchiya, Shoichi (2012)."On geometrically realizable Möbius triangulations".Discrete Mathematics.312(14): 2135–2139.doi:10.1016/j.disc.2011.06.007.MR 2921579.

[sadowsky-translation-42] Hinz, Denis F.; Fried, Eliot (2015). "Translation of Michael Sadowsky's paper" An elementary proof for the existence of a developable Möbius band and the attribution of the geometric problem to a variational problem "".Journal of Elasticity.119(1–2): 3–6.arXiv:1408.3034.doi:10.1007/s10659-014-9490-5.MR 3326180.S2CID 119733903.Reprinted inFosdick, Roger; Fried, Eliot (2016).The Mechanics of Ribbons and Möbius Bands(PDF).Springer, Dordrecht. pp. 3–6.doi:10.1007/978-94-017-7300-3.ISBN 978-94-017-7299-0.MR 3381564.

[bartels-hornung-43] Bartels, Sören; Hornung, Peter (2015). "Bending paper and the Möbius strip".Journal of Elasticity.119(1–2): 113–136.doi:10.1007/s10659-014-9501-6.MR 3326187.S2CID 119782792.Reprinted inFosdick & Fried (2016),pp. 113–136. See in particular Section 5.2, pp. 129–130.

[starostin-vdh-45] Starostin, E. L.; van der Heijden, G. H. M. (2015)."Equilibrium shapes with stress localisation for inextensible elastic Möbius and other strips".Journal of Elasticity.119(1–2): 67–112.doi:10.1007/s10659-014-9495-0.MR 3326186.S2CID 53462568.Reprinted inFosdick & Fried (2016),pp. 67–112.

[darkside-46] Schwarz, Gideon E. (1990). "The dark side of the Moebius strip".The American Mathematical Monthly.97(10): 890–897.doi:10.1080/00029890.1990.11995680.JSTOR 2324325.MR 1079975.

[halpern-weaver-47] Halpern, B.; Weaver, C. (1977)."Inverting a cylinder through isometric immersions and isometric embeddings".Transactions of the American Mathematical Society.230:41–70.doi:10.2307/1997711.JSTOR 1997711.MR 0474388.

[schwartz-48] Schwartz, Richard Evan(2021). "An improved bound on the optimal paper Moebius band".Geometriae Dedicata.215:255–267.arXiv:2008.11610.doi:10.1007/s10711-021-00648-5.MR 4330341.S2CID 220279013.

[optimal-50] Schwartz, Richard(2023). "The optimal paper Moebius band".arXiv:2308.12641[math.MG].

[crowell-51] Crowell, Rachel (September 12, 2023)."Mathematicians solve 50-year-old Möbius strip puzzle".Scientific American.

[dundas-53] Dundas, Bjørn Ian (2018). "Example 5.1.3: The unbounded Möbius band".A Short Course in Differential Topology.Cambridge Mathematical Textbooks. Cambridge University Press, Cambridge. p.https://books.google.com/books?id=7a1eDwAAQBAJ&pg=PA101.doi:10.1017/9781108349130.ISBN 978-1-108-42579-7.MR 3793640.S2CID 125997451.

[blanusa-54] Blanuša, Danilo(1954). "Le plongement isométrique de la bande de Möbius infiniment large euclidienne dans un espace sphérique, parabolique ou hyperbolique à quatre dimensions".Bulletin International de l'Académie Yougoslave des Sciences et des Beaux-Arts.12:19–23.MR 0071060.

[wunderlich-55] Wunderlich, W. (1962). "Über ein abwickelbares Möbiusband".Monatshefte für Mathematik.66(3): 276–289.doi:10.1007/BF01299052.MR 0143115.S2CID 122215321.

[schwarz-56] Schwarz, Gideon (1990)."A pretender to the title 'canonical Moebius strip'".Pacific Journal of Mathematics.143(1): 195–200.doi:10.2140/pjm.1990.143.195.MR 1047406.

[hilbert-cohn-vossen-57] Hilbert, David;Cohn-Vossen, Stephan (1952).Geometry and the Imagination(2nd ed.). Chelsea. pp. 315–316.ISBN 978-0-8284-1087-8.

[spivak-58] Spivak, Michael(1979).A Comprehensive Introduction to Differential Geometry, Volume I(2nd ed.). Wilmington, Delaware: Publish or Perish. p. 591.

[ddg-59] Knöppel, Felix (Summer 2019)."Tutorial 3: Lawson's Minimal Surfaces and the Sudanese Möbius Band".DDG2019: Visualization course at TU Berlin.

[lawson-60] Lawson, H. Blaine Jr.(1970). "Complete minimal surfaces in $S^{3}$ ".Annals of Mathematics.Second Series.92(3): 335–374.doi:10.2307/1970625.JSTOR 1970625.MR 0270280.See Section 7, pp. 350–353, where the Klein bottle is denoted $\tau _{1,2}$ .

[schleimer-segerman-61] Schleimer, Saul; Segerman, Henry (2012)."Sculptures in $S 3$ ".In Bosch, Robert; McKenna, Douglas; Sarhangi, Reza (eds.).Proceedings of Bridges 2012: Mathematics, Music, Art, Architecture, Culture.Phoenix, Arizona: Tessellations Publishing. pp. 103–110.arXiv:1204.4952.ISBN 978-1-938664-00-7.

[sudanese-62] Gunn, Charles (August 23, 2018)."Sudanese Möbius Band".Vimeo.Retrieved2022-03-17.

[franzoni-63] Franzoni, Gregorio (2012)."The Klein bottle: variations on a theme".Notices of the American Mathematical Society.59(8): 1076–1082.doi:10.1090/noti880.MR 2985809.

[huggett-jordan-64] Huggett, Stephen; Jordan, David (2009).A Topological Aperitif(Revised ed.). Springer-Verlag. p. 57.ISBN 978-1-84800-912-7.MR 2483686.

[flapan-65] Flapan, Erica(2016).Knots, Molecules, and the Universe: An Introduction to Topology.Providence, Rhode Island: American Mathematical Society. pp. 99–100.doi:10.1090/mbk/096.ISBN 978-1-4704-2535-7.MR 3443369.

[richeson-66] Richeson, David S.(2008).Euler's Gem: The Polyhedron Formula and the Birth of Topology.Princeton, New Jersey: Princeton University Press. p.171.ISBN 978-0-691-12677-7.MR 2440945.

[godinho-natario-67] Godinho, Leonor; Natário, José (2014).An Introduction to Riemannian Geometry: With Applications to Mechanics and Relativity.Universitext. Springer, Cham. pp. 152–153.doi:10.1007/978-3-319-08666-8.ISBN 978-3-319-08665-1.MR 3289090.

[cantwell-conlon-68] Cantwell, John; Conlon, Lawrence (2015). "Hyperbolic geometry and homotopic homeomorphisms of surfaces".Geometriae Dedicata.177:27–42.arXiv:1305.1379.doi:10.1007/s10711-014-9975-1.MR 3370020.S2CID 119640200.

[stillwell-69] Stillwell, John(1992). "4.6 Classification of isometries".Geometry of Surfaces.Universitext. Cham: Springer. pp. 96–98.doi:10.1007/978-1-4612-0929-4.ISBN 0-387-97743-0.MR 1171453.

[seifert-threlfall-70] Seifert, Herbert;Threlfall, William(1980).A Textbook of Topology.Pure and Applied Mathematics. Vol. 89. Translated by Goldman, Michael A. New York & London: Academic Press. p. 12.ISBN 0-12-634850-2.MR 0575168.

[lopez-martin-71] López, Francisco J.; Martín, Francisco (1997). "Complete nonorientable minimal surfaces with the highest symmetry group".American Journal of Mathematics.119(1): 55–81.doi:10.1353/ajm.1997.0004.MR 1428058.S2CID 121366986.

[meeks-72] Meeks, William H. III(1981). "The classification of complete minimal surfaces in $\mathbb {R} ^{3}$ with total curvature greater than $-8\pi$ ".Duke Mathematical Journal.48(3): 523–535.doi:10.1215/S0012-7094-81-04829-8.MR 0630583.

[systolic-73] Pesci, Adriana I.;Goldstein, Raymond E.;Alexander, Gareth P.;Moffatt, H. Keith(2015)."Instability of a Möbius strip minimal surface and a link with systolic geometry"(PDF).Physical Review Letters.114(12): 127801.Bibcode:2015PhRvL.114l7801P.doi:10.1103/PhysRevLett.114.127801.MR 3447638.PMID 25860771.

[bjorling-74] Mira, Pablo (2006). "Complete minimal Möbius strips in $\mathbb {R} ^{n}$ and the Björling problem ".Journal of Geometry and Physics.56(9): 1506–1515.Bibcode:2006JGP....56.1506M.doi:10.1016/j.geomphys.2005.08.001.MR 2240407.

[parker-75] Parker, Phillip E. (1993)."Spaces of geodesics".In Del Riego, L. (ed.).Differential Geometry Workshop on Spaces of Geometry (Guanajuato, 1992).Aportaciones Mat. Notas Investigación. Vol. 8. Soc. Mat. Mexicana, México. pp. 67–79.MR 1304924.Archived from the original on 2016-03-13.Retrieved2022-03-21.{{cite book}}:CS1 maint: bot: original URL status unknown (link)

[bickel-76] Bickel, Holger (1999). "Duality in stable planes and related closure and kernel operations".Journal of Geometry.64(1–2): 8–15.doi:10.1007/BF01229209.MR 1675956.S2CID 122209943.

[mangahas-77] Mangahas, Johanna (July 2017). "Office Hour Five: The Ping-Pong Lemma". In Clay, Matt; Margalit, Dan (eds.).Office Hours with a Geometric Group Theorist.Princeton University Press. pp. 85–105.doi:10.1515/9781400885398.ISBN 9781400885398.See in particular Project 7, pp. 104–105.

[ramirez-seade-78] Ramírez Galarza, Ana Irene; Seade, José (2007).Introduction to Classical Geometries.Basel: Birkhäuser Verlag. pp. 83–88, 157–163.ISBN 978-3-7643-7517-1.MR 2305055.

[fomenko-kunii-79] Fomenko, Anatolij T.;Kunii, Tosiyasu L. (2013).Topological Modeling for Visualization.Springer. p. 269.ISBN 9784431669562.

[isham-80] Isham, Chris J. (1999).Modern Differential Geometry for Physicists.World Scientific lecture notes in physics. Vol. 61 (2nd ed.). World Scientific. p. 269.ISBN 981-02-3555-0.MR 1698234.

[gor-oni-vin-81] Gorbatsevich, V. V.; Onishchik, A. L.; Vinberg, È. B. (1993).Lie groups and Lie algebras I: Foundations of Lie Theory; Lie Transformation Groups.Encyclopaedia of Mathematical Sciences. Vol. 20. Springer-Verlag, Berlin. pp. 164–166.doi:10.1007/978-3-642-57999-8.ISBN 3-540-18697-2.MR 1306737.

[graphene-82] Yamashiro, Atsushi; Shimoi, Yukihiro; Harigaya, Kikuo; Wakabayashi, Katsunori (2004). "Novel electronic states in graphene ribbons: competing spin and charge orders".Physica E.22(1–3): 688–691.arXiv:cond-mat/0309636.Bibcode:2004PhyE...22..688Y.doi:10.1016/j.physe.2003.12.100.S2CID 17102453.

[aromaticity1-83] Rzepa, Henry S. (September 2005). "Möbius aromaticity and delocalization".Chemical Reviews.105(10): 3697–3715.doi:10.1021/cr030092l.PMID 16218564.

[aromaticity2-84] Yoon, Zin Seok; Osuka, Atsuhiro; Kim, Dongho (May 2009). "Möbius aromaticity and antiaromaticity in expanded porphyrins".Nature Chemistry.1(2): 113–122.Bibcode:2009NatCh...1..113Y.doi:10.1038/nchem.172.PMID 21378823.

[resistor-85] "Making resistors with math".Time.Vol. 84, no. 13. September 25, 1964.

[FOOTNOTEPickover200545–46-86] Pickover (2005),pp. 45–46.

[resonator-87] Pond, J. M. (2000). "Mobius dual-mode resonators and bandpass filters".IEEE Transactions on Microwave Theory and Techniques.48(12): 2465–2471.Bibcode:2000ITMTT..48.2465P.doi:10.1109/22.898999.

[resonator2-88] Rohde, Ulrich L.; Poddar, Ajay; Sundararajan, D. (November 2013)."Printed resonators: Möbius strip theory and applications"(PDF).Microwave Journal.56(11).

[polarization-89] Bauer, Thomas; Banzer, Peter; Karimi, Ebrahim; Orlov, Sergej; Rubano, Andrea; Marrucci, Lorenzo; Santamato, Enrico; Boyd, Robert W.; Leuchs, Gerd (February 2015). "Observation of optical polarization Möbius strips".Science.347(6225): 964–966.Bibcode:2015Sci...347..964B.doi:10.1126/science.1260635.PMID 25636796.S2CID 206562350.

[can-ind-90] Candeal, Juan Carlos; Induráin, Esteban (January 1994). "The Moebius strip and a social choice paradox".Economics Letters.45(3): 407–412.doi:10.1016/0165-1765(94)90045-0.

[coaster1-91] Easdown, Martin (2012).Amusement Park Rides.Bloomsbury Publishing. p. 43.ISBN 9781782001522.

[coaster2-92] Hook, Patrick (2019).Ticket To Ride: The Essential Guide to the World's Greatest Roller Coasters and Thrill Rides.Chartwell Books. p. 20.ISBN 9780785835776.

[maps1-93] Tobler, Waldo R.(1961)."A world map on a Möbius strip".Surveying & Mapping.21:486.

[maps2-94] Kumler, Mark P.;Tobler, Waldo R. (January 1991). "Three world maps on a Moebius strip".Cartography and Geographic Information Systems.18(4): 275–276.doi:10.1559/152304091783786781.

[courant-95] Courant, Richard(1940). "Soap film experiments with minimal surfaces".The American Mathematical Monthly.47(3): 167–174.doi:10.1080/00029890.1940.11990957.JSTOR 2304225.MR 0001622.

[soap-96] Goldstein, Raymond E.;Moffatt, H. Keith;Pesci, Adriana I.;Ricca, Renzo L.(December 2010)."Soap-film Möbius strip changes topology with a twist singularity".Proceedings of the National Academy of Sciences.107(51): 21979–21984.Bibcode:2010PNAS..10721979G.doi:10.1073/pnas.1015997107.PMC3009808.

[synthesis-97] Walba, David M.; Richards, Rodney M.; Haltiwanger, R. Curtis (June 1982). "Total synthesis of the first molecular Moebius strip".Journal of the American Chemical Society.104(11): 3219–3221.doi:10.1021/ja00375a051.

[FOOTNOTEPickover200552–58-98] Pickover (2005),pp. 52–58.

[dna-99] Gitig, Diana (October 18, 2010)."Chemical origami used to create a DNA Möbius strip".Ars Technica.Retrieved2022-03-28.

[emmer-100] Emmer, Michele (Spring 1980)."Visual art and mathematics: the Moebius band".Leonardo.13(2): 108–111.doi:10.2307/1577979.JSTOR 1577979.S2CID 123908555.

[olson-101] Byers, Mark (2018).Charles Olson and American Modernism: The Practice of the Self.Oxford University Press. pp. 77–78.ISBN 9780198813255.

[escher1-102] Crato, Nuno (2010). "Escher and the Möbius strip".Figuring It Out: Entertaining Encounters with Everyday Math.Springer. pp. 123–126.doi:10.1007/978-3-642-04833-3_29.

[escher2-103] Kersten, Erik (March 13, 2017)."Möbius Strip I".Escher in the Palace.Retrieved2022-04-17.

[FOOTNOTEPickover200513-104] Pickover (2005),p. 13.

[brecher-105] Brecher, Kenneth (2017)."Art of infinity".In Swart, David; Séquin, Carlo H.; Fenyvesi, Kristóf (eds.).Proceedings of Bridges 2017: Mathematics, Art, Music, Architecture, Education, Culture.Phoenix, Arizona: Tessellations Publishing. pp. 153–158.ISBN 978-1-938664-22-9.

[peterson-106] Peterson, Ivars(2002)."Recycling topology".Mathematical Treks: From Surreal Numbers to Magic Circles.MAA Spectrum. Mathematical Association of America, Washington, DC. pp. 31–35.ISBN 0-88385-537-2.MR 1874198.

[expo74-107] "Expo '74 symbol selected".The Spokesman-Review.March 12, 1972. p. 1.

[gdrive-108] Millward, Steven (April 30, 2012)."Did Google Drive Copy its Icon From a Chinese App?".Tech in Asia.Retrieved2022-03-27– via Yahoo! News.

[impa-109] "Símbolo do IMPA".Para quem é fã do IMPA, dez curiosidades sobre o instituto.IMPA. May 7, 2020.Retrieved2022-03-27.

[FOOTNOTEPickover2005156–157-110] Pickover (2005),pp. 156–157.

[briefmarken-111] Decker, Heinz; Stark, Eberhard (1983). "Möbius-Bänder:...und natürlich auch auf Briefmarken".Praxis der Mathematik.25(7): 207–215.MR 0720681.

[architecture-112] Thulaseedas, Jolly; Krawczyk, Robert J. (2003)."Möbius concepts in architecture".In Barrallo, Javier; Friedman, Nathaniel; Maldonado, Juan Antonio; Mart\'\inez-Aroza, José; Sarhangi, Reza; Séquin, Carlo (eds.).Meeting Alhambra, ISAMA-BRIDGES Conference Proceedings.Granada, Spain: University of Granada. pp. 353–360.ISBN 84-930669-1-5.

[bridges-113] Séquin, Carlo H.(January 2018). "Möbius bridges".Journal of Mathematics and the Arts.12(2–3): 181–194.doi:10.1080/17513472.2017.1419331.S2CID 216116708.

[kazakh-114] Wainwright, Oliver (October 17, 2017)."'Norman said the president wants a pyramid': how starchitects built Astana ".The Guardian.

[nascar-115] Muret, Don (May 17, 2010)."NASCAR Hall of Fame 'looks fast sitting still'".Sports Business Journal.

[reyes-116] Gopnik, Blake (October 17, 2014)."Pedro Reyes Makes an Infinite Love Seat".Artnet News.

[zimmermann-117] Thomas, Nancy J. (October 4, 1998)."Making a Mobius a matter of mathematics".The Times (Trenton).p. aa3 – viaNewsBank.

[bagel-118] Pashman, Dan (August 6, 2015)."Cut Your Bagel The Mathematically Correct Way".The Salt.NPR.

[bacon-119] Miller, Ross (September 5, 2014)."How to make a mathematically-endless strip of bacon".The Verge.

[pasta-120] Chang, Kenneth (January 9, 2012)."Pasta Graduates From Alphabet Soup to Advanced Geometry".The New York Times.

[FOOTNOTEPickover2005174–177-121] Pickover (2005),pp. 174–177.

[FOOTNOTEPickover2005179–187-122] Pickover (2005),pp. 179–187.

[phillips-123] Phillips, Tony (November 25, 2016)."Bach and the musical Möbius strip".Plus Magazine.Reprinted from an American Mathematical Society Feature Column.

[music-125] Moskowitz, Clara(May 6, 2008)."Music reduced to beautiful math".Live Science.Retrieved2022-03-21.

[chords-126] Tymoczko, Dmitri(July 7, 2006)."The geometry of musical chords"(PDF).Science.313(5783): 72–4.Bibcode:2006Sci...313...72T.doi:10.1126/science.1126287.JSTOR 3846592.PMID 16825563.S2CID 2877171.

[bandband-127] Parks, Andrew (August 30, 2007)."Mobius Band: Friendly Fire".Magnet.

[ringvan-128] Lawson, Dom (February 9, 2021)."Ring Van Möbius".Prog.

[magic-129] Prevos, Peter (2018).The Möbius Strip in Magic: A Treatise on the Afghan Bands.Kangaroo Flat: Third Hemisphere.

[gardner-130] Gardner, Martin(1956)."The Afghan Bands".Mathematics, Magic and Mystery.New York: Dover Books. pp. 70–73.

[a]

[2]

[3]

[4]

[5]

[6]

[7]

[b]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[c]

[28]

[29]

[30]

[31]

[d]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[e]

[39]

[40]

[41]

[42]

[43]

[f]

[44]

[45]

[g]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[74]

[75]

[76]

[77]

[78]

[79]

[80]

[81]

[82]

[83]

[84]

[85]

[86]

[87]

[88]

[89]

[90]

[91]

[92]

[93]

[94]

[95]

v t e Mathematics of paper folding
Flat folding	Big-little-big lemma Crease pattern Huzita–Hatori axioms Kawasaki's theorem Maekawa's theorem Map folding Napkin folding problem Pureland origami Yoshizawa–Randlett system
Strip folding	Dragon curve Flexagon Möbius strip Regular paperfolding sequence
3d structures	Miura fold Modular origami Paper bag problem Rigid origami Schwarz lantern Sonobe Yoshimura buckling
Polyhedra	Alexandrov's uniqueness theorem Flexible polyhedron(Bricard octahedron,Steffen's polyhedron) Net Blooming Common net Source unfolding Star unfolding
Miscellaneous	Fold-and-cut theorem Lill's method
Publications	Geometric Exercises in Paper Folding Geometric Folding Algorithms Geometric Origami A History of Folding in Mathematics Origami Polyhedra Design Origamics
People	Roger C. Alperin Margherita Piazzola Beloch Yan Chen Robert Connelly Erik Demaine Martin Demaine Rona Gurkewitz David A. Huffman Tom Hull Kôdi Husimi Humiaki Huzita Toshikazu Kawasaki Robert J. Lang Anna Lubiw Jun Maekawa Kōryō Miura Joseph O'Rourke Tomohiro Tachi Eve Torrence