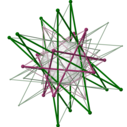
Petrie polygon
Ingeometry,aPetrie polygonfor aregular polytopeofndimensions is askew polygonin which everyn– 1consecutivesides(but non) belongs to one of thefacets.ThePetrie polygonof aregular polygonis the regular polygon itself; that of aregular polyhedronis a skew polygon such that every two consecutive sides (but no three) belongs to one of thefaces.[1]Petrie polygons are named for mathematicianJohn Flinders Petrie.
For every regular polytope there exists anorthogonal projectiononto a plane such that one Petrie polygon becomes a regular polygon with the remainder of the projection interior to it. The plane in question is theCoxeter planeof thesymmetry groupof the polygon, and the number of sides,h,is theCoxeter numberof theCoxeter group.These polygons and projected graphs are useful in visualizing symmetric structure of the higher-dimensional regular polytopes.
Petrie polygons can be defined more generally for anyembedded graph.They form the faces of another embedding of the same graph, usually on a different surface, called thePetrie dual.[2]
History
[edit]John Flinders Petrie (1907–1972) was the son ofEgyptologistsHildaandFlinders Petrie.He was born in 1907 and as a schoolboy showed remarkable promise of mathematical ability. In periods of intense concentration he could answer questions about complicated four-dimensional objects byvisualizingthem.
He first noted the importance of the regular skew polygons which appear on the surface of regular polyhedra and higher polytopes. Coxeter explained in 1937 how he and Petrie began to expand the classical subject of regular polyhedra:
- One day in 1926, J. F. Petrie told me with much excitement that he had discovered two new regular polyhedral; infinite but free of false vertices. When my incredulity had begun to subside, he described them to me: one consisting of squares, six at each vertex, and one consisting of hexagons, four at each vertex.[3]
In 1938 Petrie collaborated with Coxeter,Patrick du Val,and H. T. Flather to produceThe Fifty-Nine Icosahedrafor publication.[4] Realizing the geometric facility of the skew polygons used by Petrie, Coxeter named them after his friend when he wroteRegular Polytopes.
The idea of Petrie polygons was later extended tosemiregular polytopes.
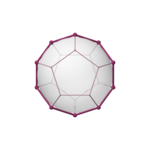
The Petrie polygons of the regular polyhedra
[edit]Theregular duals,{p,q} and {q,p}, are contained within the same projected Petrie polygon. In the images ofdual compoundson the right it can be seen that their Petrie polygons have rectangular intersections in the points where the edges touch the commonmidsphere.
| Square | Hexagon | Decagon | ||
|---|---|---|---|---|

|

|

|
|

|
| tetrahedron{3,3} | cube{4,3} | octahedron{3,4} | dodecahedron{5,3} | icosahedron{3,5} |
| edge-centered | vertex-centered | face-centered | face-centered | vertex-centered |
| V:(4,0) | V:(6,2) | V:(6,0) | V:(10,10,0) | V:(10,2) |
|
The Petrie polygons are the exterior of these orthogonal projections. | ||||
The Petrie polygons of theKepler–Poinsot polyhedraarehexagons{6} anddecagrams{10/3}.
| Hexagon | Decagram | ||
|---|---|---|---|

|

|

|

|
| gD{5,5/2} | sD{5,5/2} | gI{3,5/2} | gsD{5/2,3} |
Infinite regular skew polygons (apeirogon) can also be defined as being the Petrie polygons of the regular tilings, having angles of 90, 120, and 60 degrees of their square, hexagon and triangular faces respectively.
Infinite regular skew polygons also exist as Petrie polygons of the regular hyperbolic tilings, like theorder-7 triangular tiling,{3,7}:
The Petrie polygon of regular polychora (4-polytopes)
[edit]The Petrie polygon for the regular polychora {p,q,r} can also be determined, such that every three consecutive sides (but no four) belong to one of the polychoron's cells. As the surface of a 4-polytope is a 3-dimensional space (the3-sphere), the Petrie polygon of a regular 4-polytope is a 3-dimensional helix in this surface.
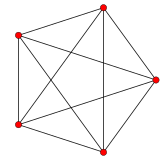 {3,3,3} 5-cell 5 sides V:(5,0) |
 {3,3,4} 16-cell 8 sides V:(8,0) |
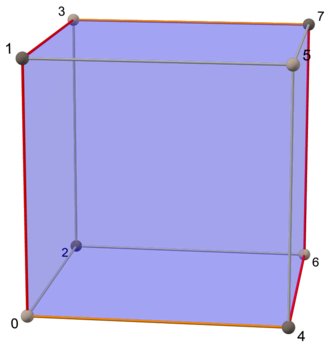
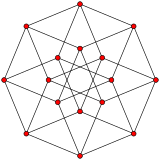 {4,3,3} tesseract 8 sides V:(8,8,0) |
 {3,4,3} 24-cell 12 sides V:(12,6,6,0) |
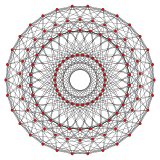 {3,3,5} 600-cell 30 sides V:(30,30,30,30,0) |
 {5,3,3} 120-cell 30 sides V:((30,60)3,603,30,60,0) |
The Petrie polygon projections of regular and uniform polytopes
[edit]The Petrie polygon projections are useful for the visualization of polytopes of dimension four and higher.
Hypercubes
[edit]Ahypercubeof dimensionnhas a Petrie polygon of size 2n,which is also the number of itsfacets.
So each of the (n− 1)-cubes forming itssurfacehasn− 1 sides of the Petrie polygon among its edges.
| Hypercubes | ||
|---|---|---|
|
The 1-cubes's Petriedigonlooks identical to the 1-cube. But the 1-cube has a single edge, while the digon has two. The images show how the Petrie polygon for dimensionn+ 1 can be constructed from that for dimensionn:
(Forn= 1 the first and the second half are the two distinct but coinciding edges of a digon.) The sides of each Petrie polygon belong to these dimensions: | ||
| Square | Cube | Tesseract |

|
|

|

|

|

|
Irreducible polytope families
[edit]This table represents Petrie polygon projections of 3 regular families (simplex,hypercube,orthoplex), and theexceptional Lie groupEnwhich generate semiregular and uniform polytopes for dimensions 4 to 8.
| Table of irreducible polytope families | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family n |
n-simplex | n-hypercube | n-orthoplex | n-demicube | 1k2 | 2k1 | k21 | pentagonal polytope | ||||||||
| Group | An | Bn |
|
|
Hn | |||||||||||
| 2 |  |
 |
 p-gon (example:p=7) |
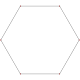 Hexagon |
 Pentagon | |||||||||||
| 3 |  Tetrahedron |
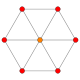 Cube |
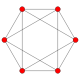 Octahedron |
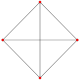 Tetrahedron |
 Dodecahedron |
 Icosahedron | ||||||||||
| 4 |  5-cell |
 |
 16-cell |
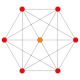 |
 24-cell |
 120-cell |
 600-cell | |||||||||
| 5 |  5-simplex |
 5-cube |
 5-orthoplex |
 5-demicube |
||||||||||||
| 6 |  6-simplex |
 6-cube |
 6-orthoplex |
 6-demicube |
 122 |
 221 |
||||||||||
| 7 |  7-simplex |
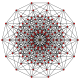 7-cube |
 7-orthoplex |
 7-demicube |
 132 |
 231 |
 321 |
|||||||||
| 8 |  8-simplex |
 8-cube |
 8-orthoplex |
 8-demicube |
 142 |
 241 |
 421 |
|||||||||
| 9 |  9-simplex |
 9-cube |
 9-orthoplex |
 9-demicube |
||||||||||||
| 10 |  10-simplex |
 10-cube |
 10-orthoplex |
 10-demicube |
||||||||||||
See also
[edit]Notes
[edit]- ^Kaleidoscopes: Selected Writings of H. S. M. Coxeter,edited by F. Arthur Sherk,Peter McMullen,Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,ISBN978-0-471-01003-6[1](Definition: paper 13, Discrete groups generated by reflections, 1933, p. 161)
- ^Pisanski, Tomaž;Randić, Milan(2000), "Bridges between geometry and graph theory", in Gorini, Catherine A. (ed.),Geometry at work,MAA Notes, vol. 53, Washington, DC: Math. Assoc. America, pp. 174–194,MR1782654.See in particularp. 181.
- ^H.S.M. Coxeter (1937) "Regular skew polyhedral in three and four dimensions and their topological analogues",Proceedings of the London Mathematical Society(2) 43: 33 to 62
- ^H. S. M. Coxeter,Patrick du Val,H. T. Flather, J. F. Petrie (1938)The Fifty-nine Icosahedra,University of Torontostudies, mathematical series 6: 1–26
- ^http://cms.math.ca/openaccess/cjm/v10/cjm1958v10.0220-0221.pdf[dead link]
References
[edit]- Coxeter,H. S. M. (1947, 63, 73)Regular Polytopes,3rd ed. New York: Dover, 1973. (sec 2.6Petrie Polygonspp. 24–25, and Chapter 12, pp. 213–235,The generalized Petrie polygon)
- Coxeter, H.S.M. (1974)Regular complex polytopes.Section 4.3 Flags and Orthoschemes, Section 11.3 Petrie polygons
- Ball, W. W. R. and H. S. M. Coxeter (1987)Mathematical Recreations and Essays,13th ed. New York: Dover. (p. 135)
- Coxeter, H. S. M. (1999)The Beauty of Geometry: Twelve Essays,Dover PublicationsLCCN99-35678
- Peter McMullen,Egon Schulte (2002)Abstract Regular Polytopes,Cambridge University Press.ISBN0-521-81496-0
- Steinberg, Robert,ON THE NUMBER OF SIDES OF A PETRIE POLYGON,2018[2]
External links
[edit]- Weisstein, Eric W."Petrie polygon".MathWorld.
- Weisstein, Eric W."Hypercube graphs".MathWorld.
- Weisstein, Eric W."Cross polytope graphs".MathWorld.
- Weisstein, Eric W."24-cell graph".MathWorld.
- Weisstein, Eric W."120-cell graph".MathWorld.
- Weisstein, Eric W."600-cell graph".MathWorld.
- Weisstein, Eric W."Gosset graph 3_21".MathWorld.