Phase portrait

Potential energyand phase portrait of asimple pendulum.Note that the x-axis, being angular, wraps onto itself after every 2π radians.

Phase portrait of damped oscillator, with increasing damping strength. The equation of motion is${\ddot {x}}+2\gamma {\dot {x}}+\omega ^{2}x=0.$

Inmathematics,aphase portraitis ageometricrepresentation of theorbitsof adynamical systemin thephase plane.Each set of initial conditions is represented by a differentpointorcurve.

Phase portraits are an invaluable tool in studying dynamical systems. They consist of aplotof typical trajectories in thephase space.This reveals information such as whether anattractor,arepellororlimit cycleis present for the chosen parameter value. The concept oftopological equivalenceis important in classifying the behaviour of systems by specifying when two different phase portraits represent the same qualitative dynamic behavior. An attractor is a stable point which is also called a "sink". The repeller is considered as an unstable point, which is also known as a "source".

A phase portrait graph of a dynamical system depicts the system's trajectories (with arrows) and stablesteady states(with dots) and unstable steady states (with circles) in a phase space. The axes are ofstate variables.

Examples

Illustration of how a phase portrait would be constructed for the motion of a simple pendulum.

Phase portrait ofvan der Pol's equation,${\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0$.

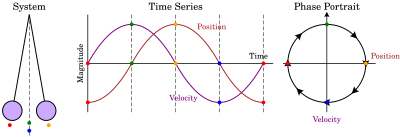
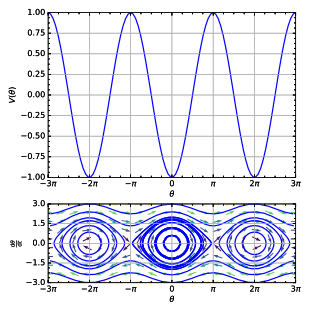
• Simple pendulum,see picture (right).
• Simpleharmonic oscillatorwhere the phase portrait is made up of ellipses centred at the origin, which is a fixed point.
• Damped harmonic motion,see animation (right).
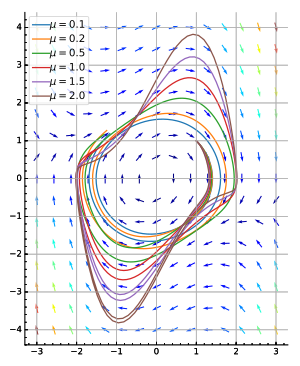
• Van der Pol oscillatorsee picture (bottom right).

Visualizing the behavior of ordinary differential equations

A phase portrait represents the directional behavior of a system ofordinary differential equations(ODEs). The phase portrait can indicate the stability of the system.

Stability

Unstable	Most of the system's solutions tend towards ∞ over time
Asymptotically stable	All of the system's solutions tend to 0 over time
Neutrally stable	None of the system's solutions tend towards ∞ over time, but most solutions do not tend towards 0 either

The phase portrait behavior of a system of ODEs can be determined by theeigenvaluesor thetraceanddeterminant(trace = λ₁+ λ₂,determinant = λ₁x λ₂) of the system.

Phase Portrait Behavior

Eigenvalue, Trace, Determinant	Phase Portrait Shape
λ1& λ2are real and of opposite sign; Determinant < 0	Saddle (unstable)
λ1& λ2are real and of the same sign, and λ1≠ λ2; 0 < determinant < (trace2/ 4)	Node (stable if trace < 0, unstable if trace > 0)
λ1& λ2have both a real and imaginary component; (trace2/ 4) < determinant	Spiral (stable if trace < 0, unstable if trace > 0)

See also

• Phase space
• Phase plane

References

• Jordan, D. W.; Smith, P. (2007).Nonlinear Ordinary Differential Equations(fourth ed.). Oxford University Press.ISBN978-0-19-920824-1.Chapter 1.
• Steven Strogatz (2001).Non-linear Dynamics and Chaos: With applications to Physics, Biology, Chemistry and Engineering.ISBN9780738204536.

External links

• Linear Phase Portraits,an MIT Mathlet.