Phasor

For other uses, seePhasor (disambiguation).

Not to be confused withphaser.

"Complex amplitude" redirects here. For the quantum-mechanical concept, seeComplex probability amplitude.

An example of seriesRLC circuitand respectivephasor diagramfor a specificω.The arrows in the upper diagram are phasors, drawn in a phasor diagram (complex planewithout axis shown), which must not be confused with the arrows in the lower diagram, which are the reference polarity for thevoltagesand the reference direction for thecurrent.

Inphysicsandengineering,aphasor(aportmanteauofphase vector) is acomplex numberrepresenting asinusoidal functionwhoseamplitude(A), andinitial phase(θ) aretime-invariantand whoseangular frequency(ω) is fixed. It is related to a more general concept calledanalytic representation,which decomposes a sinusoid into the product of a complex constant and a factor depending on time and frequency. The complex constant, which depends on amplitude and phase, is known as aphasor,orcomplex amplitude,and (in older texts)sinoror evencomplexor.

A common application is in the steady-state analysis of anelectrical networkpowered bytime varying currentwhere all signals are assumed to be sinusoidal with a common frequency. Phasor representation allows the analyst to represent the amplitude and phase of the signal using a single complex number. The only difference in their analytic representations is the complex amplitude (phasor). A linear combination of such functions can be represented as a linear combination of phasors (known asphasor arithmeticorphasor algebra) and the time/frequency dependent factor that they all have in common.

The origin of the term phasor rightfully suggests that a (diagrammatic) calculus somewhat similar to that possible forvectorsis possible for phasors as well.An important additional feature of the phasor transform is thatdifferentiationandintegrationof sinusoidal signals (having constant amplitude, period and phase) corresponds to simplealgebraic operationson the phasors; the phasor transform thus allows theanalysis(calculation) of theACsteady stateofRLC circuitsby solving simplealgebraic equations(albeit with complex coefficients) in the phasor domain instead of solvingdifferential equations(withrealcoefficients) in the time domain.The originator of the phasor transform wasCharles Proteus Steinmetzworking atGeneral Electricin the late 19th century.He got his inspiration fromOliver Heaviside.Heaviside's operational calculus was modified so that the variable p becomes jω. The complex number j has simple meaning: phase shift.

Glossing over some mathematical details, the phasor transform can also be seen as a particular case of theLaplace transform(limited to a single frequency), which, in contrast to phasor representation, can be used to (simultaneously) derive thetransient responseof an RLC circuit.However, the Laplace transform is mathematically more difficult to apply and the effort may be unjustified if only steady state analysis is required.

Fig 2. When function$A\cdot e^{i(\omega t+\theta )}$is depicted in the complex plane, the vector formed by itsimaginary and real partsrotates around the origin. Its magnitude isA,and it completes one cycle every 2π/ω.θis the angle it forms with the positive real axis att= 0(and att=n2π/ωfor allintegervalues ofn).

Notation

See also:Vector notation

Phasor notation(also known asangle notation) is amathematical notationused inelectronics engineeringandelectrical engineering.A vector whosepolar coordinatesare magnitude$A$andangle$\theta$is written$A\angle \theta.$$1\angle \theta$can represent either thevector$(\cos \theta,\,\sin \theta )$or thecomplex number$\cos \theta +i\sin \theta =e^{i\theta }$,according toEuler's formulawith$i^{2}=-1$,both of which havemagnitudesof 1.

The angle may be stated indegreeswith an implied conversion from degrees toradians.For example$1\angle 90$would be assumed to be$1\angle 90^{\circ },$which is the vector$(0,\,1)$or the number$e^{i\pi /2}=i.$

Definition

A real-valued sinusoid with constant amplitude, frequency, and phase has the form:

$A\cos(\omega t+\theta ),$

where only parameter$t$is time-variant. The inclusion of animaginary component:

$i\cdot A\sin(\omega t+\theta )$

gives it, in accordance withEuler's formula,the factoring property described in the lead paragraph:

$A\cos(\omega t+\theta )+i\cdot A\sin(\omega t+\theta )=Ae^{i(\omega t+\theta )}=Ae^{i\theta }\cdot e^{i\omega t},$

whose real part is the original sinusoid. The benefit of the complex representation is that linear operations with other complex representations produces a complex result whose real part reflects the same linear operations with the real parts of the other complex sinusoids. Furthermore, all the mathematics can be done with just the phasors$Ae^{i\theta },$and the common factor$e^{i\omega t}$is reinserted prior to the real part of the result.

The function$Ae^{i(\omega t+\theta )}$is ananalytic representationof$A\cos(\omega t+\theta ).$Figure 2 depicts it as a rotating vector in the complex plane. It is sometimes convenient to refer to the entire function as aphasor,as we do in the next section.

Arithmetic

See also:Complex number § Relations and operations

Multiplication by a constant (scalar)

Multiplication of the phasor$Ae^{i\theta }e^{i\omega t}$by a complex constant,$Be^{i\phi }$,produces another phasor. That means its only effect is to change the amplitude and phase of the underlying sinusoid: $${\begin{aligned}&\operatorname {Re} \left(\left(Ae^{i\theta }\cdot Be^{i\phi }\right)\cdot e^{i\omega t}\right)\\={}&\operatorname {Re} \left(\left(ABe^{i(\theta +\phi )}\right)\cdot e^{i\omega t}\right)\\={}&AB\cos(\omega t+(\theta +\phi )).\end{aligned}}$$

In electronics,$Be^{i\phi }$would represent animpedance,which is independent of time. In particular it isnotthe shorthand notation for another phasor. Multiplying a phasor current by an impedance produces a phasor voltage. But the product of two phasors (or squaring a phasor) would represent the product of two sinusoids, which is a non-linear operation that produces new frequency components. Phasor notation can only represent systems with one frequency, such as a linear system stimulated by a sinusoid.

Addition

The sum of phasors as addition of rotating vectors

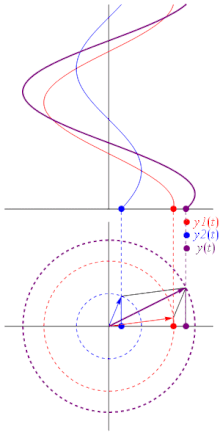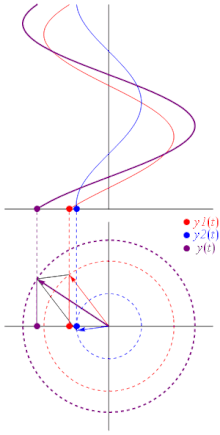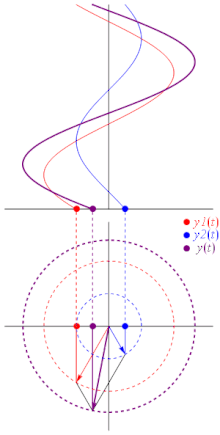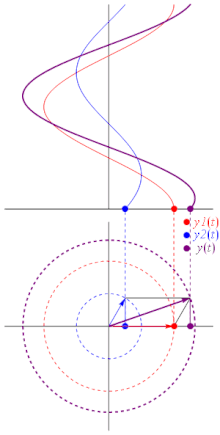
The sum of multiple phasors produces another phasor. That is because the sum of sinusoids with the same frequency is also a sinusoid with that frequency: $${\begin{aligned}&A_{1}\cos(\omega t+\theta _{1})+A_{2}\cos(\omega t+\theta _{2})\\[3pt]={}&\operatorname {Re} \left(A_{1}e^{i\theta _{1}}e^{i\omega t}\right)+\operatorname {Re} \left(A_{2}e^{i\theta _{2}}e^{i\omega t}\right)\\[3pt]={}&\operatorname {Re} \left(A_{1}e^{i\theta _{1}}e^{i\omega t}+A_{2}e^{i\theta _{2}}e^{i\omega t}\right)\\[3pt]={}&\operatorname {Re} \left(\left(A_{1}e^{i\theta _{1}}+A_{2}e^{i\theta _{2}}\right)e^{i\omega t}\right)\\[3pt]={}&\operatorname {Re} \left(\left(A_{3}e^{i\theta _{3}}\right)e^{i\omega t}\right)\\[3pt]={}&A_{3}\cos(\omega t+\theta _{3}),\end{aligned}}$$ where: $$A_{3}^{2}=(A_{1}\cos \theta _{1}+A_{2}\cos \theta _{2})^{2}+(A_{1}\sin \theta _{1}+A_{2}\sin \theta _{2})^{2},$$

and, if we take${\textstyle \theta _{3}\in \left[-{\frac {\pi }{2}},{\frac {3\pi }{2}}\right]}$,then$\theta _{3}$is:

• ${\textstyle \operatorname {sgn}(A_{1}\sin(\theta _{1})+A_{2}\sin(\theta _{2}))\cdot {\frac {\pi }{2}},}$if$A_{1}\cos \theta _{1}+A_{2}\cos \theta _{2}=0,$with$\operatorname {sgn}$thesignum function;
• $\arctan \left({\frac {A_{1}\sin \theta _{1}+A_{2}\sin \theta _{2}}{A_{1}\cos \theta _{1}+A_{2}\cos \theta _{2}}}\right),$if$A_{1}\cos \theta _{1}+A_{2}\cos \theta _{2}>0$;
• $\pi +\arctan \left({\frac {A_{1}\sin \theta _{1}+A_{2}\sin \theta _{2}}{A_{1}\cos \theta _{1}+A_{2}\cos \theta _{2}}}\right),$if$A_{1}\cos \theta _{1}+A_{2}\cos \theta _{2}<0$.

or, via thelaw of cosineson thecomplex plane(or thetrigonometric identity for angle differences): $$A_{3}^{2}=A_{1}^{2}+A_{2}^{2}-2A_{1}A_{2}\cos(180^{\circ }-\Delta \theta )=A_{1}^{2}+A_{2}^{2}+2A_{1}A_{2}\cos(\Delta \theta ),$$ where$\Delta \theta =\theta _{1}-\theta _{2}.$

A key point is thatA₃andθ₃do not depend onωort,which is what makes phasor notation possible. The time and frequency dependence can be suppressed and re-inserted into the outcome as long as the only operations used in between are ones that produce another phasor. Inangle notation,the operation shown above is written: $$A_{1}\angle \theta _{1}+A_{2}\angle \theta _{2}=A_{3}\angle \theta _{3}.$$

Another way to view addition is that twovectorswith coordinates[A₁cos(ωt+θ₁),A₁sin(ωt+θ₁)]and[A₂cos(ωt+θ₂),A₂sin(ωt+θ₂)]areadded vectoriallyto produce a resultant vector with coordinates[A₃cos(ωt+θ₃),A₃sin(ωt+θ₃)](see animation).

Phasor diagram of three waves in perfect destructive interference

In physics, this sort of addition occurs when sinusoidsinterferewith each other, constructively or destructively. The static vector concept provides useful insight into questions like this: "What phase difference would be required between three identical sinusoids for perfect cancellation?" In this case, simply imagine taking three vectors of equal length and placing them head to tail such that the last head matches up with the first tail. Clearly, the shape which satisfies these conditions is an equilateraltriangle,so the angle between each phasor to the next is 120° (2π⁄3radians), or one third of a wavelengthλ⁄3.So the phase difference between each wave must also be 120°, as is the case inthree-phase power.

In other words, what this shows is that: $$\cos(\omega t)+\cos \left(\omega t+{\frac {2\pi }{3}}\right)+\cos \left(\omega t-{\frac {2\pi }{3}}\right)=0.$$

In the example of three waves, the phase difference between the first and the last wave was 240°, while for two waves destructive interference happens at 180°. In the limit of many waves, the phasors must form a circle for destructive interference, so that the first phasor is nearly parallel with the last. This means that for many sources, destructive interference happens when the first and last wave differ by 360 degrees, a full wavelength$\lambda$.This is why in single slitdiffraction,the minima occur whenlightfrom the far edge travels a full wavelength further than the light from the near edge.

As the single vector rotates in an anti-clockwise direction, its tip at point A will rotate one complete revolution of 360° or 2πradians representing one complete cycle. If the length of its moving tip is transferred at different angular intervals in time to a graph as shown above, a sinusoidal waveform would be drawn starting at the left with zero time. Each position along the horizontal axis indicates the time that has elapsed since zero time,t= 0.When the vector is horizontal the tip of the vector represents the angles at 0°, 180°, and at 360°.

Likewise, when the tip of the vector is vertical it represents the positive peak value, (+A_max) at 90° orπ⁄2and the negative peak value, (−A_max) at 270° or3π⁄2.Then the time axis of the waveform represents the angle either in degrees or radians through which the phasor has moved. So we can say that a phasor represents a scaled voltage or current value of a rotating vector which is "frozen" at some point in time, (t) and in our example above, this is at an angle of 30°.

Sometimes when we are analysing alternating waveforms we may need to know the position of the phasor, representing the alternating quantity at some particular instant in time especially when we want to compare two different waveforms on the same axis. For example, voltage and current. We have assumed in the waveform above that the waveform starts at timet= 0with a corresponding phase angle in either degrees or radians.

But if a second waveform starts to the left or to the right of this zero point, or if we want to represent in phasor notation the relationship between the two waveforms, then we will need to take into account this phase difference,Φof the waveform. Consider the diagram below from the previous Phase Difference tutorial.

Differentiation and integration

The timederivativeorintegralof a phasor produces another phasor.For example: $${\begin{aligned}&\operatorname {Re} \left({\frac {\mathrm {d} }{\mathrm {d} t}}{\mathord {\left(Ae^{i\theta }\cdot e^{i\omega t}\right)}}\right)\\={}&\operatorname {Re} \left(Ae^{i\theta }\cdot i\omega e^{i\omega t}\right)\\={}&\operatorname {Re} \left(Ae^{i\theta }\cdot e^{i\pi /2}\omega e^{i\omega t}\right)\\={}&\operatorname {Re} \left(\omega Ae^{i(\theta +\pi /2)}\cdot e^{i\omega t}\right)\\={}&\omega A\cdot \cos \left(\omega t+\theta +{\frac {\pi }{2}}\right).\end{aligned}}$$

Therefore, in phasor representation, the time derivative of a sinusoid becomes just multiplication by the constant${\textstyle i\omega =e^{i\pi /2}\cdot \omega }$.

Similarly, integrating a phasor corresponds to multiplication by${\textstyle {\frac {1}{i\omega }}={\frac {e^{-i\pi /2}}{\omega }}.}$The time-dependent factor,$e^{i\omega t},$is unaffected.

When we solve alinear differential equationwith phasor arithmetic, we are merely factoring$e^{i\omega t}$out of all terms of the equation, and reinserting it into the answer. For example, consider the following differential equation for the voltage across thecapacitorin anRC circuit: $${\frac {\mathrm {d} \,v_{\text{C}}(t)}{\mathrm {d} t}}+{\frac {1}{RC}}v_{\text{C}}(t)={\frac {1}{RC}}v_{\text{S}}(t).$$

When the voltage source in this circuit is sinusoidal: $$v_{\text{S}}(t)=V_{\text{P}}\cdot \cos(\omega t+\theta ),$$

we may substitute$v_{\text{S}}(t)=\operatorname {Re} \left(V_{\text{s}}\cdot e^{i\omega t}\right).$

$$v_{\text{C}}(t)=\operatorname {Re} \left(V_{\text{c}}\cdot e^{i\omega t}\right),$$ where phasor$V_{\text{s}}=V_{\text{P}}e^{i\theta },$and phasor$V_{\text{c}}$is the unknown quantity to be determined.

In the phasor shorthand notation, the differential equation reduces to: $$i\omega V_{\text{c}}+{\frac {1}{RC}}V_{\text{c}}={\frac {1}{RC}}V_{\text{s}}.$$

Derivation

${\frac {\mathrm {d} }{\mathrm {d} t}}\operatorname {Re} \left(V_{\text{c}}\cdot e^{i\omega t}\right)+{\frac {1}{RC}}\operatorname {Re} (V_{\text{c}}\cdot e^{i\omega t})={\frac {1}{RC}}\operatorname {Re} \left(V_{\text{s}}\cdot e^{i\omega t}\right)$ (Eq.1)

Since this must hold for all$t$,specifically:${\textstyle t-{\frac {\pi }{2\omega }},}$it follows that:

${\frac {\mathrm {d} }{\mathrm {d} t}}\operatorname {Im} \left(V_{\text{c}}\cdot e^{i\omega t}\right)+{\frac {1}{RC}}\operatorname {Im} \left(V_{\text{c}}\cdot e^{i\omega t}\right)={\frac {1}{RC}}\operatorname {Im} \left(V_{\text{s}}\cdot e^{i\omega t}\right).$ (Eq.2)

It is also readily seen that: $${\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} t}}\operatorname {Re} \left(V_{\text{c}}\cdot e^{i\omega t}\right)&=\operatorname {Re} \left({\frac {\mathrm {d} }{\mathrm {d} t}}{\mathord {\left(V_{\text{c}}\cdot e^{i\omega t}\right)}}\right)=\operatorname {Re} \left(i\omega V_{\text{c}}\cdot e^{i\omega t}\right)\\{\frac {\mathrm {d} }{\mathrm {d} t}}\operatorname {Im} \left(V_{\text{c}}\cdot e^{i\omega t}\right)&=\operatorname {Im} \left({\frac {\mathrm {d} }{\mathrm {d} t}}{\mathord {\left(V_{\text{c}}\cdot e^{i\omega t}\right)}}\right)=\operatorname {Im} \left(i\omega V_{\text{c}}\cdot e^{i\omega t}\right).\end{aligned}}$$

Substituting these intoEq.1andEq.2,multiplyingEq.2by$i,$and adding both equations gives: $${\begin{aligned}i\omega V_{\text{c}}\cdot e^{i\omega t}+{\frac {1}{RC}}V_{\text{c}}\cdot e^{i\omega t}&={\frac {1}{RC}}V_{\text{s}}\cdot e^{i\omega t}\\\left(i\omega V_{\text{c}}+{\frac {1}{RC}}V_{\text{c}}\right)\!\cdot e^{i\omega t}&=\left({\frac {1}{RC}}V_{\text{s}}\right)\cdot e^{i\omega t}\\i\omega V_{\text{c}}+{\frac {1}{RC}}V_{\text{c}}&={\frac {1}{RC}}V_{\text{s}}.\end{aligned}}$$

Solving for the phasor capacitor voltage gives: $$V_{\text{c}}={\frac {1}{1+i\omega RC}}\cdot V_{\text{s}}={\frac {1-i\omega RC}{1+(\omega RC)^{2}}}\cdot V_{\text{P}}e^{i\theta }.$$

As we have seen, the factor multiplying$V_{\text{s}}$represents differences of the amplitude and phase of$v_{\text{C}}(t)$relative to$V_{\text{P}}$and$\theta.$

In polar coordinate form, the first term of the last expression is: $${\frac {1-i\omega RC}{1+(\omega RC)^{2}}}={\frac {1}{\sqrt {1+(\omega RC)^{2}}}}\cdot e^{-i\phi (\omega )},$$ where$\phi (\omega )=\arctan(\omega RC)$.

Therefore: $$v_{\text{C}}(t)=\operatorname {Re} \left(V_{\text{c}}\cdot e^{i\omega t}\right)={\frac {1}{\sqrt {1+(\omega RC)^{2}}}}\cdot V_{\text{P}}\cos(\omega t+\theta -\phi (\omega )).$$

Ratio of phasors

A quantity called compleximpedanceis the ratio of two phasors, which is not a phasor, because it does not correspond to a sinusoidally varying function.

Applications

Circuit laws

With phasors, the techniques for solvingDCcircuits can be applied to solve linear AC circuits.

Ohm's law for resistors

Aresistorhas no time delays and therefore doesn't change the phase of a signal thereforeV=IRremains valid.

Ohm's law for resistors, inductors, and capacitors

V=IZwhereZis the compleximpedance.

Kirchhoff's circuit laws

Work with voltages and current as complex phasors.

In an AC circuit we have real power (P) which is a representation of the average power into the circuit and reactive power (Q) which indicates power flowing back and forth. We can also define thecomplex powerS=P+jQand the apparent power which is the magnitude ofS.The power law for an AC circuit expressed in phasors is thenS=VI^*(whereI^*is thecomplex conjugateofI,and the magnitudes of the voltage and current phasorsVand ofIare theRMSvalues of the voltage and current, respectively).

Given this we can apply the techniques ofanalysis of resistive circuitswith phasors to analyze single frequency linear AC circuits containing resistors, capacitors, andinductors.Multiple frequency linear AC circuits and AC circuits with different waveforms can be analyzed to find voltages and currents by transforming all waveforms to sine wave components (usingFourier series) with magnitude and phase then analyzing each frequency separately, as allowed by thesuperposition theorem.This solution method applies only to inputs that are sinusoidal and for solutions that are in steady state, i.e., after all transients have died out.

The concept is frequently involved in representing anelectrical impedance.In this case, the phase angle is thephase differencebetween the voltage applied to the impedance and the current driven through it.

Power engineering

In analysis ofthree phaseAC power systems, usually a set of phasors is defined as the three complexcube roots of unity,graphically represented as unit magnitudes at angles of 0, 120 and 240 degrees. By treating polyphase AC circuit quantities as phasors, balanced circuits can be simplified and unbalanced circuits can be treated as an algebraic combination ofsymmetrical components.This approach greatly simplifies the work required in electrical calculations of voltage drop, power flow, and short-circuit currents. In the context of power systems analysis, the phase angle is often given indegrees,and the magnitude inRMSvalue rather than the peak amplitude of the sinusoid.

The technique ofsynchrophasorsuses digital instruments to measure the phasors representing transmission system voltages at widespread points in a transmission network. Differences among the phasors indicate power flow and system stability.

Telecommunications: analog modulations

A: phasor representation of amplitude modulation, B: alternate representation of amplitude modulation, C: phasor representation of frequency modulation, D: alternate representation of frequency modulation

The rotating frame picture using phasor can be a powerful tool to understand analog modulations such asamplitude modulation(and its variants) andfrequency modulation.

$$x(t)=\operatorname {Re} \left(Ae^{i\theta }\cdot e^{i2\pi f_{0}t}\right),$$ where the term in brackets is viewed as a rotating vector in the complex plane.

The phasor has length$A$,rotates anti-clockwise at a rate of$f_{0}$revolutions per second, and at time$t=0$makes an angle of$\theta$with respect to the positive real axis.

The waveform$x(t)$can then be viewed as a projection of this vector onto the real axis. A modulated waveform is represented by this phasor (the carrier) and two additional phasors (the modulation phasors). If the modulating signal is a single tone of the form$Am\cos {2\pi f_{m}t}$,where$m$is the modulation depth and$f_{m}$is the frequency of the modulating signal, then for amplitude modulation the two modulation phasors are given by,

$${1 \over 2}Ame^{i\theta }\cdot e^{i2\pi (f_{0}+f_{m})t},$$ $${1 \over 2}Ame^{i\theta }\cdot e^{i2\pi (f_{0}-f_{m})t}.$$

The two modulation phasors are phased such that their vector sum is always in phase with the carrier phasor. An alternative representation is two phasors counter rotating around the end of the carrier phasor at a rate$f_{m}$relative to the carrier phasor. That is,

$${1 \over 2}Ame^{i\theta }\cdot e^{i2\pi f_{m}t},$$ $${1 \over 2}Ame^{i\theta }\cdot e^{-i2\pi f_{m}t}.$$

Frequency modulation is a similar representation except that the modulating phasors are not in phase with the carrier. In this case the vector sum of the modulating phasors is shifted 90° from the carrier phase. Strictly, frequency modulation representation requires additional small modulation phasors at$2f_{m},3f_{m}$etc, but for most practical purposes these are ignored because their effect is very small.

See also

• In-phase and quadrature components
  • Constellation diagram
• Analytic signal,a generalization of phasors for time-variant amplitude, phase, and frequency.
  • Complex envelope
• Phase factor,a phasor of unit magnitude

Further reading

• Douglas C. Giancoli (1989).Physics for Scientists and Engineers.Prentice Hall.ISBN0-13-666322-2.
• Dorf, Richard C.; Tallarida, Ronald J. (1993-07-15).Pocket Book of Electrical Engineering Formulas(1 ed.). Boca Raton, FL: CRC Press. pp. 152–155.ISBN0849344735.

External links

• Phasor Phactory
• Visual Representation of Phasors
• Polar and Rectangular Notation
• Phasor in Telecommunication