Plane-based geometric algebra

Elements of 3D Plane-based GA, which includes planes, lines, and points. All elements are constructed from reflections in planes. Lines are a special case of rotations.

Plane-based geometric algebrais an application ofClifford algebrato modelling planes, lines, points, andrigid transformations.Generally this is with the goal of solving applied problems involving these elements and theirintersections,projections,and their angle from one another in 3D space.Originally growing out of research onspin groups,it was developed with applications toroboticsin mind.It has since been applied to machine learning,rigid body dynamics,and computer science,especiallycomputer graphics.It is usually combined with adualityoperation into a system known as "Projective Geometric Algebra", see below.

Plane-based geometric algebra takesplanar reflectionsas basic elements, and constructs all other transformations and geometric objects out of them. Formally: it identifies planar reflections with thegrade-1elements of a Clifford Algebra, that is, elements that are written with a single subscript such as "${\boldsymbol {e}}_{1}$".With some rare exceptions described below, the algebra is almost alwaysCl_3,0,1(R),meaning it has three basis grade-1 elements whose square is$1$and a single basis element whose square is$0$.

Plane-based GA subsumes thequaternionandaxis-anglerepresentations of rotations in its rotors and bivectors respectively

Plane-based GA subsumes a large number of algebraic constructions applied in engineering, including theaxis–angle representationof rotations, thequaternionanddual quaternionrepresentations of rotations and translations, theplücker representation of lines,thepoint normal representation of planes,and thehomogeneous representationof points. Dual Quaternions then allow thescrew, twist and wrenchmodel of classical mechanics to be constructed.

The plane-based approach to geometry may be contrasted with the approach that uses thecross product,in which points, translations, rotation axes, and plane normals are all modelled as "vectors". However, use of vectors in advanced engineering problems often require subtle distinctions between different kinds of vector because of this, includingGibbs vectors,pseudovectorsandcontravariant vectors.The latter of these two, in plane-based GA, map to the concepts of "rotation axis" and "point", with the distinction between them being made clear by the notation: rotation axes such as${\boldsymbol {e}}_{13}$(two lower indices) are always notated differently than points such as${\boldsymbol {e}}_{123}$(three lower indices).

All objects considered below are still "vectors" in the technical sense that they areelements of vector spaces;however they arenot(generally) vectors in the sense that one could meaningfully take their cross product - so it is not informative to visualize them as arrows. Therefore to avoid conflict over different algebraic and visual connotations coming from the word 'vector', this article avoids use of the word.

Construction

In Plane-based GA, grade-1 elements are planes and can be used to perform planar reflections; grade-2 elements are lines and can be used to perform "line reflections"; grade-3 elements are points and can be used to perform "point reflections". Rotations and translations are constructed out of these elements; line reflections in particular are the same things as 180-degree rotations.

Plane-based geometric algebra starts with planes and then constructs lines and points by takingintersectionsof planes. Its canonicalbasisconsists of the plane such that$x=0$,which is labelled${\boldsymbol {e}}_{1}$,the$y=0$,which is labelled${\boldsymbol {e}}_{2}$,and the$z=0$plane,${\boldsymbol {e}}_{3}$.

Other planes may be obtained as weighted sums of the basis planes. for example,${\boldsymbol {e}}_{2}+{\boldsymbol {e}}_{3}$would be the plane midway between the y- and z-plane. In general, combining two geometric objects in plane-based GA will always be as a weighted average of them – combining points will give a point between them, as will combining lines, and indeed rotations.

An operation that is as fundamental as addition is thegeometric product.For example:

${\boldsymbol {e}}_{1}{\boldsymbol {e}}_{23}={\boldsymbol {e}}_{123}$

Here we take${\boldsymbol {e}}_{1}$,which is a planar reflection in the$x=0$plane, and${\boldsymbol {e}}_{23}$,which is a 180-degree rotation around the x-axis. Their geometric product is${\boldsymbol {e}}_{123}$,which is a point reflection in the origin, because that is the transformation that results from a 180-degree rotation followed by a planar reflection in a plane orthogonal to the rotation's axis.

For any pair of elements${\textstyle A}$and$B$,their geometric product${\textstyle A}$$B$is the transformation$B$followed by the transformation${\textstyle A}$.Note that transformcompositionisnottransformapplication;for example${\boldsymbol {e}}_{1}{\boldsymbol {e}}_{23}$isnot"${\boldsymbol {e}}_{23}$transformed by${\boldsymbol {e}}_{1}$",it is instead the transform${\boldsymbol {e}}_{23}$followed by the transform${\boldsymbol {e}}_{1}$.Transform application is implemented with thesandwich product,see below.

This geometric interpretation is usually combined with the following assertion:

${\boldsymbol {e}}_{1}{\boldsymbol {e}}_{1}=1\qquad {\boldsymbol {e}}_{2}{\boldsymbol {e}}_{2}=1\qquad {\boldsymbol {e}}_{3}{\boldsymbol {e}}_{3}=1\qquad {\boldsymbol {e}}_{0}{\boldsymbol {e}}_{0}=0$

The geometric interpretation of the first three defining equations is that if we perform the same planar reflection twice we get back to where we started; e.g. any grade-1 element (plane) multiplied by itself results in theidentity function,"$1$".The statement that${\boldsymbol {e}}_{0}{\boldsymbol {e}}_{0}=0$is more subtle.

Plane-based GA includes elements "at infinity". A star in the night sky is an intuitive example of a "point at infinity", in the sense that it defines some direction, but practically speaking it is impossible to reach. The milky way forms a hazy stripe of stars across the sky; it behaves, in some sense, like a "line at infinity". The sky itself is a "plane at infinity".

Elements at infinity

The algebraic element${\boldsymbol {e}}_{0}$represents theplane at infinity.It behaves differently from any other plane – intuitively, it can be "approached but never reached". In 3 dimensions,${\boldsymbol {e}}_{0}$can be visualized as the sky. Lying in it are the points called "vanishing points",or alternatively" ideal points ", or" points at infinity ". Parallel lines such as metal rails on a railway line meet one another at such points.

Lines at infinity also exist; thehorizon lineis an example of such a line. For an observer standing on a plane, all planes parallel to the plane they stand on meet one another at the horizon line. Algebraically, if we take${\boldsymbol {e}}_{2}$to be the ground, then${\boldsymbol {e}}_{2}+5{\boldsymbol {e}}_{0}$will be a plane parallel to the ground (displaced 5 meters from it). These two parallel planes meet one another at the line-at-infinity${\boldsymbol {e}}_{02}$.

Most lines, for examples${\boldsymbol {e}}_{23}$,can act as axes forrotations;in fact they can treated as imaginaryquaternions.But lines that lie in the plane-at-infinity${\boldsymbol {e}}_{0}$,such as the line${\boldsymbol {e}}_{30}$,cannot act as axes for a "rotation". Instead, these are axes for translations, and instead of having an algebra resembling complex numbers or quaternions, their algebraic behaviour is the same as thedual numbers,since they square to 0. Combining the three basis lines-through-the-origin${\boldsymbol {e}}_{23}$,${\boldsymbol {e}}_{13}$,${\boldsymbol {e}}_{12}$,which square to$-1$,with the three basis lines at infinity${\boldsymbol {e}}_{10}$,${\boldsymbol {e}}_{20}$,${\boldsymbol {e}}_{30}$gives the necessary elements for (Plücker) coordinates of lines.

Derivation of other operations from the geometric product

The orange objects here are projected onto the green objects to get the dark grey objects, all using the unified projection formula (a·b)b⁻¹. Since PGA includes points, lines, and planes, this involves projection of planes onto points, points onto planes, lines onto planes, etc.

There are several useful products that can be extracted from the geometric product, similar to how thedot productandcross productwere extracted from thequaternion product.These include:

1. The transformation from$A$toward$B$is$B{\tilde {A}}$,with$A$and$B$again being points, lines or planes; here,${\tilde {A}}$is thereverse(essentially the inverse). The transformation will be by twice the angle or distance between$A$and$B$;if a transformation by the exact distance or angle is required, it can be obtained with the dual quaternion exponential and logarithm.
2. The meet (or "wedgeproduct ")$\wedge$,which is useful for takingintersectionsof objects; for example, the intersection of the plane$P$with the line$L$is the point$P\wedge L$.
3. Theinnerproduct$\cdot$,which is useful for takingprojectionsof objects onto other objects; the projection of$A$onto$B$is$(A\cdot B){\tilde {B}}$– this formula holds whether the objects are points, lines, or planes.
4. Thenormof$A$is${\sqrt {A{\tilde {A}}}}$and is denoted$\lVert A\rVert$.It can be used to take angles between most objects: the angle between$A$and$B$,whether they are lines or planes, is$\arccos(\lVert A\cdot B\rVert )$.This assumes that$A$and$B$both havenorm$1$,eg$\lVert A\rVert =\lVert B\rVert =1$.Thus it can be seen that the inner product is a generalization of thedot product.
5. Application of anyrigid transformation(dual quaternion) or reflection${\textstyle T}$to any object, including points, lines, planes and indeed other rigid transformations, is${\textstyle TA{\tilde {T}}}$,where${\textstyle A}$is object to be transformed; this is the "sandwich product".
6. The commutator product$\times$,defined as${\textstyle {\frac {1}{2}}(AB-BA)}$.This is a generalization of theLie Bracket:if${\textstyle A}$is the logarithm of a transformation being undergone by$B$,we have that the derivative of$B$with respect to time is${\textstyle A}$$\times$$B$.It is also the case that for lines$A$and$B$we have that${\textstyle A}$$\times$$B$is the unique line that is orthogonal to both.

For example, recall that${\boldsymbol {e}}_{1}$is a plane, as is${\boldsymbol {e}}_{1}+{\boldsymbol {e}}_{2}+{\boldsymbol {e}}_{0}$.Their geometric product is their "reflection composition" – a reflection in${\boldsymbol {e}}_{1}$followed by a reflection in${\boldsymbol {e}}_{1}+{\boldsymbol {e}}_{2}+{\boldsymbol {e}}_{0}$,which results in the dual quaternion$1+{\boldsymbol {e}}_{12}+{\boldsymbol {e}}_{10}$.But this may be more than is desired; if we wish to take only the intersection line of the two planes, we simply need to look at just the "grade-2 part" of this result, e.g. the part with two lower indices${\boldsymbol {e}}_{12}+{\boldsymbol {e}}_{10}$.The information needed to specify that the intersection line is contained inside the transform composition of the two planes, because a reflection in a pair of planes will result in a rotation around their intersection line.

Interpretation as algebra of reflections

The center of the picture is a point that is performing apoint reflectionon the tetrahedron. In 3D plane-based GA, points 3-reflections. Algebraically this means they are grade-3 – but their geometric interpretation is very different from the usual geometric interpretation of a "trivector" as an "oriented volume element".

The algebra of all distance-preserving transformations (essentially, rigid transformations and reflections) in 3D is called theEuclidean Group,$E(3)$.By theCartan–Dieudonné theorem,any element of it can be written as a series of reflections in planes.

In plane-based GA, essentially all geometric objects can be thought of as a transformation. Planes such as${\boldsymbol {e}}_{1}$are planar reflections, points such as${\boldsymbol {e}}_{123}$arepoint reflections,and lines such as${\boldsymbol {e}}_{12}$are line reflections - which in 3D are the same thing as 180-degree rotations. The identity transform is the unique object that is constructed out of zero reflections. All of these are elements of$E(3)$.

Some elements of$E(3)$,for example rotations by any angle that isnot180 degrees, do not have a single specific geometric object which is used to visualize them; nevertheless, they can always be thought of as being made up of reflections, and can always be represented as alinear combinationof some elements of objects in plane-based geometric algebra. For example,$0.8+0.6{\boldsymbol {e}}_{12}$is a slight rotation about the${\boldsymbol {e}}_{12}$axis, and it can be written as a geometric product (a transform composition) of${\boldsymbol {e}}_{1}$and$0.8{\boldsymbol {e}}_{1}+0.6{\boldsymbol {e}}_{2}$,both of which are planar reflections intersecting at the line${\boldsymbol {e}}_{12}$.

In fact, any rotation can be written as a composition of two planar reflections that pass through its axis; thus it can be called a2-reflection.Rotoreflections,glide reflections,andpoint reflectionscan also always be written as compositions of 3 planar reflections and so are called 3-reflections. The upper limit of this for 3D is ascrew motion,which is a 4-reflection. For this reason, when considering screw motions, it is necessary to use the grade-4 element of 3D plane-based GA,${\boldsymbol {e}}_{0123}$,which is the highest-grade element.

Geometric interpretation of geometric product as "cancelling out" reflections

When viewed as a composition of reflections, rotations and translations, both have onegaugedegree of freedom. The yellow cube is a reflection of the black cube; the green cube is a reflection of the yellow cube. But while the yellow cube changes as the planes change, the final green cube will be unchanged while the reflection planes have the same angle/distance and intersect in the same line (which may be a line at infinity).

A reflection in a plane followed by a reflection in thesameplane results in no change. The algebraic interpretation for this geometry is that grade-1 elements such as${\boldsymbol {e}}_{1}$square to1.This simple fact can be used to give a geometric interpretation for the general behaviour of the geometric product as a device that solves geometric problems by "cancelling mirrors".

To give an example of the usefulness of this, suppose we wish to find a plane orthogonal to a certain lineLin 3D and passing through a certain pointP.Lis a 2-reflection and$P$is a 3-reflection, so taking their geometric productPLin some sense produces a 5-reflection; however, as in the picture below, two of these reflections cancel, leaving a 3-reflection (sometimes known as arotoreflection). In the plane-based geometric algebra notation, this rotoreflection can be thought of as a planar reflection "added to" a point reflection. The plane part of this rotoreflection is the plane that is orthogonal to the lineLand the original pointP.A similar procedure can be used to find the line orthogonal to a plane and passing through a point, or the intersection of a line and a plane, or the intersection line of a plane with another plane.

A transformation in 2D that takes a blue triangle to a red triangle, simplified using "gauging". The full transformation was composed from four reflections. Two of the reflection lines, gauged so that they coincide, can be "cancelled".

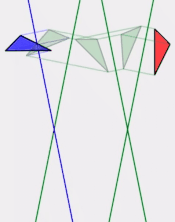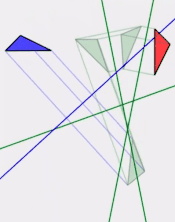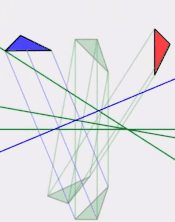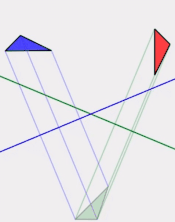
Rotations and translations aseven subalgebra

Rotations and translations are transformations that preservedistancesandhandedness(chirality), e.g. when they are applied to sets of objects, the relative distances between those objects does not change; nor does their handedness, which is to say that a right-handed glove will not turn into a left-handed glove. All transformations in 3D euclidean plane-based geometric algebra preserve distances, but reflections, rotoreflections, and transflections do not preserve handedness.

Rotations and translationsdopreserve handedness, which in 3D Plane-based GA implies that they can be written as a composition of aneven numberof reflections. A rotations can thought of as a reflection in a plane followed by a reflection in another plane which isnotparallel to the first (thequaternions,which are set in the context of PGA above). If the planes were parallel, composing their reflections would give a translation.

Rotations and translations are both special cases ofscrew motions,e.g. a rotation around a line in space followed by a translation directed along the same line. This group is usually calledSE(3),the group ofSpecial (handedness-preserving)Euclidean (distance-preserving) transformations in3dimensions. This group has two commonly-used representations that allow them to be used in algebra and computation, one being the 4×4 matrices of real numbers, and the other being theDual Quaternions.The Dual Quaternion representation (like the usual quaternions) is actually adouble coverof SE(3). Since the Dual Quaternions are closed under multiplication and addition and are made from an even number of basis elements in, they are called theeven subalgebraof 3D euclidean (plane-based) geometric algebra. The word 'spinor' is sometimes used to describe this subalgebra.

Describing rigid transformations using planes was a major goal in the work ofCamille Jordan.andMichel Chaslessince it allows the treatment to be dimension-independent.

Generalizations

Planar reflections are a special case ofsphere inversions,the 2D version of which is a circle inversion, depicted here.

Inversive Geometry

Inversive geometry is the study of geometric objects and behaviours generated byinversions in circles and spheres.Reflections in planes are a special case of inversions in spheres, because a plane is a sphere with infinite radius. Since plane-based geometric algebra is generated by composition of reflections, it is a special case of inversive geometry. Inversive geometry itself can be performed with the larger system known asConformal Geometric Algebra(CGA), of which Plane-based GA is asubalgebra.

CGA is also usually applied to 3D space, and is able to model general spheres, circles, andconformal(angle-preserving) transformations, which include the transformations seen on thePoincare disk.It can be difficult to see the connection between PGA and CGA, since CGA is often "point based", although some authors take a plane-based approach to CGAwhich makes the notations for Plane-based GA and CGA identical.

Projective Geometric Algebra

The pointsPandQdefine the lineg;this can be written asP∨Q=g,with∨being theregressive productof Projective Geometric Algebra, a system which subsumes Plane-based Geometric Algebra.

Plane-based geometric algebra is able to represent all Euclidean transformations, but in practice it is almost always combined with adualoperation of some kind to create the larger system known as "Projective Geometric Algebra", PGA.Duality, as in other Clifford andGrassmann algebras,allows a definition of theregressive product.This is extremely useful for engineering applications - in plane-based GA, the regressive product canjoina point to another point to obtain a line, and can join a point and a line to obtain a plane. It has the further convenience that if any two elements (points, lines, or planes) havenorm(see above) equal to$1$,the norm of their regressive product is equal to the distance between them. The join of several points is also known as theiraffine hull.

Variants of duality and terminology

There is variation across authors as to the precise definition given for dual that is used to define the regressive product in PGA. No matter which definition is given, the regressive product functions to give completely identical outputs; for this reason, precise discussion of the dual is usually not included in introductory material on projective geometric algebra. There are significant conceptual and philosophical differences:

1. TheHodgedualrelates elements of plane-based geometric algebra to other elements of plane based geometric algebra (eg, other euclidean transformations); for example, the Hodge dual of a planar reflection is a point reflection. PGA was originally defined using the Hodge dual.
2. TheProjectivedualalso maps planes to points, but it isnotthe case that both are reflections; instead, the projective dual switches between the space that plane-based geometric algebra operates in and a different,non-euclideanspace, seedual space.For example, planes in plane-based geometric algebra, which perform planar reflections, are mapped to points in dual space which are involved incollineations.Different authors have termed the plane-based GA part of PGA "Euclidean space"and "Antispace".This form of duality, combined with the fact that geometric objects are represented homogeneously (meaning that multiplication by scalars does not change them), is the reason that the system is known as "Projective" Geometric Algebra (even though it does not contain the full projective group, unlike Conformal Geometric Algebra, which contains the full conformal group).
3. Alternatively, conformal geometric algebra can be used (since plane-based GA is a subalgebra of CGA), but defining the PGA regressive product within it is complicated by the fact that CGA has its own regressive product, which is a different product. Loosely because the join of three points in CGA is acircle,whereas in PGA it is a plane. Another problem is that PGA "points" have a fundamentally different algebraic representation than CGA points; to compare the two algebras, PGA points must be recognized as CGApoint pairs,where the pair has one point at infinity. To get around this problem, some authors define the projective dual described above, in CGA, as an exchange of two different PGA-isomorphic subalgebras within it.

Projective geometric algebra of non-euclidean geometries and Classical Lie Groups in 3 dimensions

To a first approximation, the physical world is euclidean, i.e. most transformations arerigid;Projective Geometric Algebra is therefore usually based onCl_3,0,1(R),since rigid transformations can be modelled in this algebra. However, it is possible to model other spaces by slightly varying the algebra.

Geometric space	Transformation group	Apparent "plane at infinity" squares to	Names for handedness-preserving subgroup (even subalgebra)	Notes
Euclidean	Pin(3, 0, 1) Cl3,0,1(R)	0	Dual quaternions;Spin(3, 0, 1); double cover ofrigid transformations	Most important for engineering applications, since transformations are rigid; also most "intuitive" for humans
Elliptic	Pin(4, 0, 0) Cl4,0,0(R)	1	Split-biquaternions;Spin(4, 0, 0); double cover of4D rotations	Also known as "spherical geometry". Analogous toCl3,0,0(R);provides a model theGnonomic world map projection.IncludesPoincaré duality.
Hyperbolic	Pin(3, 1, 0) Cl3,1,0(R)	−1	Complex quaternion;Spin(3, 1, 0); double cover ofLorentz group	Also known as "saddle geometry". Group can perform rotations andspacetime boosts,a.k.a. boosts.(2,1,0)is equivalent to theKlein disk model of 2D hyperbolic geometry.

Plane-based GA usually handles the (3D version of) the middle case here. But we instead choose to have a basis element squaring to1or−1instead of 0, euclidean geometry can be changed to spherical or hyperbolic geometry.

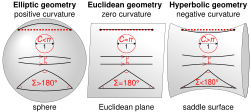
In these systems, the points, planes, and lines have the same coordinates that they have in plane-based GA. But transformations like rotations and reflections will have very different effects on the geometry. In all cases below, the algebra is a double cover of the group of reflections, rotations, and rotoreflections in the space.

All formulae from the euclidean case carry over to these other geometries – the meet still functions as a way of taking the intersection of objects; the geometric product still functions as a way of composing transformations; and in the hyperbolic case the inner product become able to measurehyperbolic angle.

All three even subalgebras areclassical Lie groups(after taking the quotient by scalars). The associatedLie algebrafor each group is the grade 2 elements of the Clifford algebra,nottaking the quotient by scalars.