Euclidean plane

"Plane (geometry)" redirects here. For generalizations, seePlane (mathematics).For its applications, seePlane (physics).

Bi-dimensionalCartesian coordinate system

Inmathematics,aEuclidean planeis aEuclidean spaceofdimension two,denoted${\textbf {E}}^{2}$or$\mathbb {E} ^{2}$.It is ageometric spacein which tworeal numbersare required to determine thepositionof eachpoint.It is anaffine space,which includes in particular the concept ofparallel lines.It has alsometrical propertiesinduced by adistance,which allows to definecircles,andangle measurement.

A Euclidean plane with a chosenCartesian coordinate systemis called aCartesian plane. The set$\mathbb {R} ^{2}$of the ordered pairs of real numbers (thereal coordinate plane), equipped with thedot product,is often calledthe Euclidean plane,since every Euclidean plane isisomorphicto it.

History

See also:Euclidean geometry § History

Books I through IV and VI ofEuclid's Elementsdealt with two-dimensional geometry, developing such notions as similarity of shapes, thePythagorean theorem(Proposition 47), equality of angles andareas,parallelism, the sum of the angles in a triangle, and the three cases in which triangles are "equal" (have the same area), among many other topics.

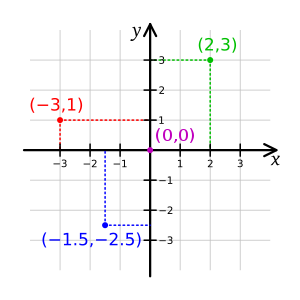
Later, the plane was described in a so-calledCartesian coordinate system,acoordinate systemthat specifies eachpointuniquely in aplaneby a pair ofnumericalcoordinates,which are thesigneddistances from the point to two fixedperpendiculardirected lines, measured in the sameunit of length.Each reference line is called acoordinate axisor justaxisof the system, and the point where they meet is itsorigin,usually at ordered pair (0, 0). The coordinates can also be defined as the positions of theperpendicular projectionsof the point onto the two axes, expressed as signed distances from the origin.

The idea of this system was developed in 1637 in writings by Descartes and independently byPierre de Fermat,although Fermat also worked in three dimensions, and did not publish the discovery.Both authors used a single (abscissa) axis in their treatments, with the lengths ofordinatesmeasured along lines not-necessarily-perpendicular to that axis.The concept of using a pair of fixed axes was introduced later, after Descartes'La Géométriewas translated into Latin in 1649 byFrans van Schootenand his students. These commentators introduced several concepts while trying to clarify the ideas contained in Descartes' work.

Later, the plane was thought of as afield,where any two points could be multiplied and, except for 0, divided. This was known as thecomplex plane.The complex plane is sometimes called the Argand plane because it is used in Argand diagrams. These are named afterJean-Robert Argand(1768–1822), although they were first described by Danish-Norwegian land surveyor and mathematicianCaspar Wessel(1745–1818).Argand diagrams are frequently used to plot the positions of thepolesandzeroesof afunctionin the complex plane.

In geometry

See also:Euclidean geometry

Coordinate systems

Main articles:Rectangular coordinate systemandPolar coordinate system

"Plane coordinates" redirects here. Not to be confused withCoordinate plane.

In mathematics,analytic geometry(also called Cartesian geometry) describes every point in two-dimensional space by means of two coordinates. Two perpendicularcoordinate axesare given which cross each other at theorigin.They are usually labeledxandy.Relative to these axes, the position of any point in two-dimensional space is given by an ordered pair of real numbers, each number giving the distance of that point from theoriginmeasured along the given axis, which is equal to the distance of that point from the other axis.

Another widely used coordinate system is thepolar coordinate system,which specifies a point in terms of its distance from the origin and its angle relative to a rightward reference ray.

• 
  Cartesian coordinate system
• 
  Polar coordinate system

Embedding in three-dimensional space

This section is an excerpt fromEuclidean planes in three-dimensional space.[edit]

Plane equation in normal form

InEuclidean geometry,aplaneis aflattwo-dimensionalsurfacethat extends indefinitely. Euclidean planes often arise assubspacesofthree-dimensional space$\mathbb {R} ^{3}$. A prototypical example is one of a room's walls, infinitely extended and assumed infinitesimal thin.

While a pair of real numbers$\mathbb {R} ^{2}$suffices to describe points on a plane, the relationship with out-of-plane points requires special consideration for theirembeddingin theambient space$\mathbb {R} ^{3}$.

Polytopes

Main article:Polygon

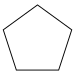
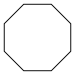
In two dimensions, there are infinitely many polytopes: the polygons. The first few regular ones are shown below:

Convex

TheSchläfli symbol$\{n\}$represents aregularn-gon.

Name	Triangle (2-simplex)	Square (2-orthoplex) (2-cube)	Pentagon	Hexagon	Heptagon	Octagon
Schläfli symbol	{3}	{4}	{5}	{6}	{7}	{8}
Image
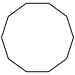
Name	Nonagon	Decagon	Hendecagon	Dodecagon	Tridecagon	Tetradecagon
Schläfli	{9}	{10}	{11}	{12}	{13}	{14}
Image
Name	Pentadecagon	Hexadecagon	Heptadecagon	Octadecagon	Enneadecagon	Icosagon	...n-gon
Schläfli	{15}	{16}	{17}	{18}	{19}	{20}	{n}
Image

Degenerate (spherical)

The regularmonogon(or henagon) {1} and regulardigon{2} can be considered degenerate regular polygons and exist nondegenerately in non-Euclidean spaces like a2-sphere,2-torus,orright circular cylinder.

Name	Monogon	Digon
Schläfli	{1}	{2}
Image

Non-convex

There exist infinitely many non-convex regular polytopes in two dimensions, whose Schläfli symbols consist of rational numbers {n/m}. They are calledstar polygonsand share the samevertex arrangementsof the convex regular polygons.

In general, for any natural number n, there are n-pointed non-convex regular polygonal stars with Schläfli symbols {n/m} for allmsuch thatm<n/2 (strictly speaking {n/m} = {n/(n−m)}) andmandnarecoprime.

Name	Pentagram	Heptagrams		Octagram	Enneagrams		Decagram	...n-agrams
Schläfli	{5/2}	{7/2}	{7/3}	{8/3}	{9/2}	{9/4}	{10/3}	{n/m}
Image

Circle

Main article:Circle

Thehyperspherein 2 dimensions is acircle,sometimes called a 1-sphere (S¹) because it is a one-dimensionalmanifold.In a Euclidean plane, it has the length 2πrand theareaof itsinterioris

$A=\pi r^{2}$

where$r$is the radius.

Other shapes

Main article:List of two-dimensional geometric shapes

There are an infinitude of other curved shapes in two dimensions, notably including theconic sections:theellipse,theparabola,and thehyperbola.

In linear algebra

Another mathematical way of viewing two-dimensional space is found inlinear algebra,where the idea of independence is crucial. The plane has two dimensions because the length of arectangleis independent of its width. In the technical language of linear algebra, the plane is two-dimensional because every point in the plane can be described by a linear combination of two independentvectors.

Dot product, angle, and length

Main article:Dot product

The dot product of two vectorsA= [A₁,A₂]andB= [B₁,B₂]is defined as:

$\mathbf {A} \cdot \mathbf {B} =A_{1}B_{1}+A_{2}B_{2}$

A vector can be pictured as an arrow. Its magnitude is its length, and its direction is the direction the arrow points. The magnitude of a vectorAis denoted by$\|\mathbf {A} \|$.In this viewpoint, the dot product of two Euclidean vectorsAandBis defined by

$\mathbf {A} \cdot \mathbf {B} =\|\mathbf {A} \|\,\|\mathbf {B} \|\cos \theta,$

where θ is theanglebetweenAandB.

The dot product of a vectorAby itself is

$\mathbf {A} \cdot \mathbf {A} =\|\mathbf {A} \|^{2},$

which gives

$\|\mathbf {A} \|={\sqrt {\mathbf {A} \cdot \mathbf {A} }},$

the formula for theEuclidean lengthof the vector.

In calculus

Gradient

In a rectangular coordinate system, the gradient is given by

$\nabla f={\frac {\partial f}{\partial x}}\mathbf {i} +{\frac {\partial f}{\partial y}}\mathbf {j} \,.$

Line integrals and double integrals

For somescalar fieldf:U⊆R²→R,the line integral along apiecewise smoothcurveC⊂Uis defined as

$\int \limits _{C}f\,ds=\int _{a}^{b}f(\mathbf {r} (t))|\mathbf {r} '(t)|\,dt,$

wherer:[a, b] →Cis an arbitrarybijectiveparametrizationof the curveCsuch thatr(a) andr(b) give the endpoints ofCand$a<b$.

For avector fieldF:U⊆R²→R²,the line integral along apiecewise smoothcurveC⊂U,in the direction ofr,is defined as

$\int \limits _{C}\mathbf {F} (\mathbf {r} )\cdot \,d\mathbf {r} =\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt,$

where · is thedot productandr:[a, b] →Cis abijectiveparametrizationof the curveCsuch thatr(a) andr(b) give the endpoints ofC.

Adouble integralrefers to anintegralwithin a regionDinR²of afunction$f(x,y),$and is usually written as:

$\iint \limits _{D}f(x,y)\,dx\,dy.$

Fundamental theorem of line integrals

Main article:Fundamental theorem of line integrals

Thefundamental theorem of line integralssays that aline integralthrough agradientfield can be evaluated by evaluating the original scalar field at the endpoints of the curve.

Let$\varphi:U\subseteq \mathbb {R} ^{2}\to \mathbb {R}$.Then

$\varphi \left(\mathbf {q} \right)-\varphi \left(\mathbf {p} \right)=\int _{\gamma [\mathbf {p},\mathbf {q} ]}\nabla \varphi (\mathbf {r} )\cdot d\mathbf {r},$

withp,qthe endpoints of the curve γ.

Green's theorem

Main article:Green's theorem

LetCbe a positivelyoriented,piecewise smooth,simple closed curvein aplane,and letDbe the region bounded byC.IfLandMare functions of (x,y) defined on anopen regioncontainingDand havecontinuouspartial derivativesthere, then

$\oint _{C}(L\,dx+M\,dy)=\iint _{D}\left({\frac {\partial M}{\partial x}}-{\frac {\partial L}{\partial y}}\right)\,dx\,dy$

where the path of integration along C iscounterclockwise.

In topology

Intopology,the plane is characterized as being the uniquecontractible2-manifold.

Its dimension is characterized by the fact that removing a point from the plane leaves a space that is connected, but notsimply connected.

In graph theory

Ingraph theory,aplanar graphis agraphthat can beembeddedin the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other.Such a drawing is called aplane graphorplanar embedding of the graph.A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to aplane curveon that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

See also

• Geometric space
• Planimetrics

References

Works cited

• Burton, David M. (2011),The History of Mathematics / An Introduction(7th ed.), McGraw Hill,ISBN978-0-07-338315-6