Polygonal chain

A simple polygonal chain

A self-intersecting polygonal chain

A closed polygonal chain

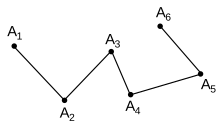
Ingeometry,apolygonal chainis a connected series ofline segments.More formally, a polygonal chain⁠$P$⁠is acurvespecified by asequenceof points$(A_{1},A_{2},\dots,A_{n})$called itsvertices.The curve itself consists of the line segments connecting the consecutive vertices.

Variations

Simple

Asimple polygonal chainis one in which only consecutive segments intersect and only at their endpoints.

Closed

Aclosed polygonal chainis one in which the first vertex coincides with the last one, or, alternatively, the first and the last vertices are also connected by a line segment. A simple closed polygonal chain inthe planeis the boundary of asimple polygon.Often the term "polygon"is used in the meaning of" closed polygonal chain ", but in some cases it is important to draw a distinction between apolygonal areaand a polygonal chain. Aspaceclosed polygonal chain is also known as askew "polygon".

Monotone

A set ofn=17 points has a polygonal path with 4 same-sign slopes

A polygonal chain is calledmonotoneif there is astraight lineLsuch that every line perpendicular toLintersects the chain at most once. Every nontrivial monotone polygonal chain is open. In comparison, amonotone polygonis a polygon (a closed chain) that can be partitioned into exactly two monotone chains.The graphs ofpiecewise linear functionsform monotone chains with respect to a horizontal line.

Parametrization

Each segment of a polygonal chain is typicallyparametrizedlinearly, usinglinear interpolationbetween successive vertices. For the whole chain, two parametrizations are common in practical applications: Each segment of the chain can be assigned a unitintervalof the parameter corresponding to the index of the first vertex; alternately, each segment of the chain can be assigned an interval of the parameter corresponding to the length of the segment, so that the parameter corresponds uniformly to arclength along the whole chain.

From point sets

Every set of at least$n$points contains a polygonal path of at least$\lfloor {\sqrt {n-1}}\rfloor$edges in which all slopes have the same sign. This is a corollary of theErdős–Szekeres theorem.

Applications

Polygonal chains can often be used to approximate more complex curves. In this context, theRamer–Douglas–Peucker algorithmcan be used to find a polygonal chain with few segments that serves as an accurate approximation.

Ingraph drawing,polygonal chains are often used to represent the edges of graphs, in drawing styles where drawing the edges as straight line segments would cause crossings, edge-vertex collisions, or other undesired features. In this context, it is often desired to draw edges with as few segments and bends as possible, to reduce the visual clutter in the drawing; the problem of minimizing the number of bends is calledbend minimization.

A red Bézier curve is defined by the control pointsP₀, ..., P₄.The gray polygonal chain connecting the control points is called the control polygon.

Incomputer-aided geometric design,smooth curves are often defined by a list ofcontrol points,e.g. in definingBézier curvesegments. When connected together, the control points form a polygonal chain called acontrol polygon.

Polygonal chains are also a fundamental data type incomputational geometry.For instance, apoint locationalgorithm ofLeeandPreparataoperates by decomposing arbitraryplanar subdivisionsinto an ordered sequence of monotone chains, in which a point location query problem may be solved bybinary search;this method was later refined to give optimal time bounds for the point location problem.

Withgeographic information system,linestrings may represent any linear geometry, and can be described using thewell-known textmarkup as aLineStringorMultiLineString.Linear rings (orLinearRing) are closed and simple polygonal chains used to build polygon geometries.

See also

• Chain (algebraic topology),a formal combination of simplices that in the 1-dimensional case includes polygonal chains
• Composite Bézier curve,a generalization that replaces each straight line of a polygonal chain with a smooth curve.
• Link distance,the number of segments of the shortest chain that links two points within a polygon
• Piecewise regression
• Path (graph theory),an analogous concept in abstract graphs
• Polyhedral terrain,a 3D generalization of a monotone polygonal chain
• Spirangle,a spiral polygonal chain
• Stick number,a knot invariant based on representing a knot as a closed polygonal chain
• Traverse,application insurveying