Jump to content

Power diagram

From Wikipedia, the free encyclopedia
A power diagram of four circles

Incomputational geometry,apower diagram,also called aLaguerre–Voronoi diagram,Dirichlet cell complex,radical Voronoi tesselationor asectional Dirichlet tesselation,is a partition of theEuclidean planeintopolygonalcells defined from a set of circles. The cell for a given circleCconsists of all the points for which thepower distancetoCis smaller than the power distance to the other circles. The power diagram is a form of generalizedVoronoi diagram,and coincides with the Voronoi diagram of the circle centers in the case that all the circles have equal radii.[1][2][3][4]

Definition[edit]

The power of a pointPoutside of a given circle

IfCis a circle andPis a point outsideC,then thepowerofPwith respect toCis the square of the length of a line segment fromPto a pointTof tangency withC.Equivalently, ifPhas distancedfrom the center of the circle, and the circle has radiusr,then (by thePythagorean theorem) the power isd2−r2.The same formulad2−r2may be extended to all points in the plane, regardless of whether they are inside or outside ofC:points onChave zero power, and points insideChave negative power.[2][3][4]

The power diagram of a set ofncirclesCiis a partition of the plane intonregionsRi(called cells), such that a pointPbelongs toRiwhenever circleCiis the circle minimizing the power ofP.[2][3][4]

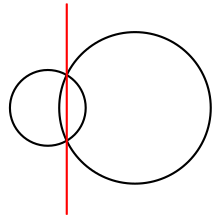
The radical axis of two intersecting circles. The power diagram of the two circles is the partition of the plane into two halfplanes formed by this line.

In the casen= 2, the power diagram consists of twohalfplanes,separated by a line called theradical axisor chordale of the two circles. Along the radical axis, both circles have equal power. More generally, in any power diagram, each cellRiis aconvex polygon,the intersection of the halfspaces bounded by the radical axes of circleCiwith each other circle. Triples of cells meet atverticesof the diagram, which are the radical centers of the three circles whose cells meet at the vertex.[2][3][4]

Related constructions[edit]

The power diagram may be seen as a weighted form of theVoronoi diagramof a set of point sites, a partition of the plane into cells within which one of the sites is closer than all the other sites. Other forms ofweighted Voronoi diagraminclude the additively weighted Voronoi diagram, in which each site has a weight that is added to its distance before comparing it to the distances to the other sites, and the multiplicatively weighted Voronoi diagram, in which the weight of a site is multiplied by its distance before comparing it to the distances to the other sites. In contrast, in the power diagram, we may view each circle center as a site, and each circle's squared radius as a weight that is subtracted from thesquared Euclidean distancebefore comparing it to other squared distances. In the case that all the circle radii are equal, this subtraction makes no difference to the comparison, and the power diagram coincides with the Voronoi diagram.[3][4]

A planar power diagram may also be interpreted as a planar cross-section of an unweighted three-dimensional Voronoi diagram. In this interpretation, the set of circle centers in the cross-section plane are the perpendicular projections of the three-dimensional Voronoi sites, and the squared radius of each circle is a constantKminus the squared distance of the corresponding site from the cross-section plane, whereKis chosen large enough to make all these radii positive.[5]

Like the Voronoi diagram, the power diagram may be generalized to Euclidean spaces of any dimension. The power diagram ofnspheres inddimensions is combinatorially equivalent to the intersection of a set ofnupward-facing halfspaces ind+ 1 dimensions, and vice versa.[3]

Algorithms and applications[edit]

Two-dimensional power diagrams may be constructed by an algorithm that runs in time O(nlogn).[2][3]More generally, because of the equivalence with higher-dimensional halfspace intersections,d-dimensional power diagrams (ford> 2) may be constructed by an algorithm that runs in time.[3]

The power diagram may be used as part of an efficient algorithm for computing the volume of a union of spheres. Intersecting each sphere with its power diagram cell gives its contribution to the total union, from which the volume may be computed in time proportional to the complexity of the power diagram.[6]

Other applications of power diagrams includedata structuresfor testing whether a point belongs to a union of disks,[2]algorithms for constructing the boundary of a union of disks,[2]and algorithms for finding the closest two balls in a set of balls.[7]It is also used for solving the semi-discreteoptimal transportationproblem[8]which in turn has numerous applications, such as early universe reconstruction[9]or fluid dynamics.[10]

History[edit]

Aurenhammer (1987)traces the definition of the power distance to the work of 19th-century mathematiciansEdmond LaguerreandGeorgy Voronoy.[3]Fejes Tóth (1977)defined power diagrams and used them to show that the boundary of a union ofncircular disks can always be illuminated from at most 2npoint light sources.[11]Power diagrams have appeared in the literature under other names including the "Laguerre–Voronoi diagram", "Dirichlet cell complex", "radical Voronoi tesselation" and "sectional Dirichlet tesselation".[12]

References[edit]

  1. ^Linhart, J. (1981), "Dirichletsche Zellenkomplexe mit maximaler Eckenzahl",Geometriae Dedicata,11(3): 363–367,doi:10.1007/BF00149360,MR0627538,S2CID120072781.
  2. ^abcdefgImai, Hiroshi; Iri, Masao; Murota, Kazuo (1985), "Voronoĭ diagram in the Laguerre geometry and its applications",SIAM Journal on Computing,14(1): 93–105,doi:10.1137/0214006,MR0774929.
  3. ^abcdefghiAurenhammer, F.(1987), "Power diagrams: properties, algorithms and applications",SIAM Journal on Computing,16(1): 78–96,doi:10.1137/0216006,MR0873251.
  4. ^abcdeEdelsbrunner, Herbert(1987), "13.6 Power Diagrams",Algorithms in Combinatorial Geometry,EATCS Monographs on Theoretical Computer Science, vol. 10, Springer-Verlag, pp. 327–328.
  5. ^Ash, Peter F.; Bolker, Ethan D. (1986), "Generalized Dirichlet tessellations",Geometriae Dedicata,20(2): 209–243,doi:10.1007/BF00164401,MR0833848,S2CID120383767.
  6. ^Avis, David;Bhattacharya, Binay K.; Imai, Hiroshi (1988),"Computing the volume of the union of spheres"(PDF),The Visual Computer,3(6): 323–328,doi:10.1007/BF01901190.
  7. ^Guibas, Leonidas;Zhang, Li (1998), "Euclidean proximity and power diagrams",10th Canadian Conference on Computational Geometry.
  8. ^Aurenhammer, F.; Hoffmann, F.; Aronov, B. (January 1998)."Minkowski-Type Theorems and Least-Squares Clustering".Algorithmica.20(1): 61–76.doi:10.1007/PL00009187.ISSN0178-4617.S2CID5409198.
  9. ^Levy, Bruno; Mohayaee, Roya; von Hausegger, Sebastian (2021-07-13)."A fast semidiscrete optimal transport algorithm for a unique reconstruction of the early Universe".Monthly Notices of the Royal Astronomical Society.506(1): 1165–1185.arXiv:2012.09074.doi:10.1093/mnras/stab1676.ISSN0035-8711.
  10. ^Lévy, Bruno (February 2022)."Partial optimal transport for a constant-volume Lagrangian mesh with free boundaries".Journal of Computational Physics.451:110838.arXiv:2106.03936.Bibcode:2022JCoPh.45110838L.doi:10.1016/j.jcp.2021.110838.S2CID235406800.
  11. ^Fejes Tóth, L.(1977), "Illumination of convex discs",Acta Mathematica Academiae Scientiarum Hungaricae,29(3–4): 355–360,doi:10.1007/BF01895856,MR0464065,S2CID122510545.
  12. ^Aurenhammer, F.; Imai, H. (1988), "Geometric relations among Voronoĭ diagrams",Geometriae Dedicata,27(1): 65–75,doi:10.1007/BF00181613,MR0950323.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Power_diagram&oldid=1213122502"