Probability density function

Box plotand probability density function of anormal distributionN(0, σ²).

Geometric visualisation of themode,medianandmeanof an arbitrary unimodal probability density function.

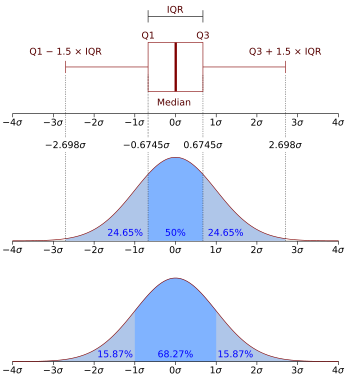
Inprobability theory,aprobability density function(PDF),density function,ordensityof anabsolutely continuous random variable,is afunctionwhose value at any given sample (or point) in thesample space(the set of possible values taken by the random variable) can be interpreted as providing arelative likelihoodthat the value of the random variable would be equal to that sample.Probability density is the probability per unit length, in other words, while theabsolute likelihoodfor a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample.

More precisely, the PDF is used to specify the probability of therandom variablefallingwithin a particular range of values,as opposed to taking on any one value. This probability is given by theintegralof this variable's PDF over that range—that is, it is given by the area under the density function but above the horizontal axis and between the lowest and greatest values of the range. The probability density function is nonnegative everywhere, and the area under the entire curve is equal to 1.

The termsprobability distribution functionandprobability functionhave also sometimes been used to denote the probability density function. However, this use is not standard among probabilists and statisticians. In other sources, "probability distribution function" may be used when theprobability distributionis defined as a function over general sets of values or it may refer to thecumulative distribution function,or it may be aprobability mass function(PMF) rather than the density. "Density function" itself is also used for the probability mass function, leading to further confusion.In general though, the PMF is used in the context ofdiscrete random variables(random variables that take values on a countable set), while the PDF is used in the context of continuous random variables.

Example

Examples of four continuous probability density functions.

Suppose bacteria of a certain species typically live 20 to 30 hours. The probability that a bacterium livesexactly5 hours is equal to zero. A lot of bacteria live for approximately 5 hours, but there is no chance that any given bacterium dies at exactly 5.00... hours. However, the probability that the bacterium dies between 5 hours and 5.01 hours is quantifiable. Suppose the answer is 0.02 (i.e., 2%). Then, the probability that the bacterium dies between 5 hours and 5.001 hours should be about 0.087, since this time interval is one-tenth as long as the previous. The probability that the bacterium dies between 5 hours and 5.0001 hours should be about 0.0087, and so on.

In this example, the ratio (probability of living during an interval) / (duration of the interval) is approximately constant, and equal to 2 per hour (or 2 hour⁻¹). For example, there is 0.02 probability of dying in the 0.01-hour interval between 5 and 5.01 hours, and (0.02 probability / 0.01 hours) = 2 hour⁻¹.This quantity 2 hour⁻¹is called the probability density for dying at around 5 hours. Therefore, the probability that the bacterium dies at 5 hours can be written as (2 hour⁻¹)dt.This is the probability that the bacterium dies within an infinitesimal window of time around 5 hours, wheredtis the duration of this window. For example, the probability that it lives longer than 5 hours, but shorter than (5 hours + 1 nanosecond), is (2 hour⁻¹)×(1 nanosecond) ≈6×10⁻¹³(using theunit conversion3.6×10¹²nanoseconds = 1 hour).

There is a probability density functionfwithf(5 hours) = 2 hour⁻¹.Theintegraloffover any window of time (not only infinitesimal windows but also large windows) is the probability that the bacterium dies in that window.

Absolutely continuous univariate distributions

A probability density function is most commonly associated withabsolutely continuousunivariate distributions.Arandom variable$X$has density$f_{X}$,where$f_{X}$is a non-negativeLebesgue-integrablefunction, if: $$\Pr[a\leq X\leq b]=\int _{a}^{b}f_{X}(x)\,dx.$$

Hence, if$F_{X}$is thecumulative distribution functionof$X$,then: $$F_{X}(x)=\int _{-\infty }^{x}f_{X}(u)\,du,$$ and (if$f_{X}$is continuous at$x$) $$f_{X}(x)={\frac {d}{dx}}F_{X}(x).$$

Intuitively, one can think of$f_{X}(x)\,dx$as being the probability of$X$falling within the infinitesimalinterval$[x,x+dx]$.

Formal definition

(This definition may be extended to any probability distribution using themeasure-theoreticdefinition of probability.)

Arandom variable$X$with values in ameasurable space$({\mathcal {X}},{\mathcal {A}})$(usually$\mathbb {R} ^{n}$with theBorel setsas measurable subsets) has asprobability distributionthe measureX_∗Pon$({\mathcal {X}},{\mathcal {A}})$:thedensityof$X$with respect to a reference measure$\mu$on$({\mathcal {X}},{\mathcal {A}})$is theRadon–Nikodym derivative: $$f={\frac {dX_{*}P}{d\mu }}.$$

That is,fis any measurable function with the property that: $$\Pr[X\in A]=\int _{X^{-1}A}\,dP=\int _{A}f\,d\mu$$ for any measurable set$A\in {\mathcal {A}}.$

Discussion

In thecontinuous univariate case above,the reference measure is theLebesgue measure.Theprobability mass functionof adiscrete random variableis the density with respect to thecounting measureover the sample space (usually the set ofintegers,or some subset thereof).

It is not possible to define a density with reference to an arbitrary measure (e.g. one can not choose the counting measure as a reference for a continuous random variable). Furthermore, when it does exist, the density is almost unique, meaning that any two such densities coincidealmost everywhere.

Further details

Unlike a probability, a probability density function can take on values greater than one; for example, thecontinuous uniform distributionon the interval[0, 1/2]has probability densityf(x) = 2for0 ≤x≤ 1/2andf(x) = 0elsewhere.

Thestandard normal distributionhas probability density $$f(x)={\frac {1}{\sqrt {2\pi }}}\,e^{-x^{2}/2}.$$

If a random variableXis given and its distribution admits a probability density functionf,then theexpected valueofX(if the expected value exists) can be calculated as $$\operatorname {E} [X]=\int _{-\infty }^{\infty }x\,f(x)\,dx.$$

Not every probability distribution has a density function: the distributions ofdiscrete random variablesdo not; nor does theCantor distribution,even though it has no discrete component, i.e., does not assign positive probability to any individual point.

A distribution has a density function if and only if itscumulative distribution functionF(x)isabsolutely continuous.In this case:Fisalmost everywheredifferentiable,and its derivative can be used as probability density: $${\frac {d}{dx}}F(x)=f(x).$$

If a probability distribution admits a density, then the probability of every one-point set{a}is zero; the same holds for finite and countable sets.

Two probability densitiesfandgrepresent the sameprobability distributionprecisely if they differ only on a set ofLebesguemeasure zero.

In the field ofstatistical physics,a non-formal reformulation of the relation above between the derivative of thecumulative distribution functionand the probability density function is generally used as the definition of the probability density function. This alternate definition is the following:

Ifdtis an infinitely small number, the probability thatXis included within the interval(t,t+dt)is equal tof(t)dt,or: $$\Pr(t<X<t+dt)=f(t)\,dt.$$

Link between discrete and continuous distributions

It is possible to represent certain discrete random variables as well as random variables involving both a continuous and a discrete part with ageneralizedprobability density function using theDirac delta function.(This is not possible with a probability density function in the sense defined above, it may be done with adistribution.) For example, consider a binary discreterandom variablehaving theRademacher distribution—that is, taking −1 or 1 for values, with probability1⁄2each. The density of probability associated with this variable is: $$f(t)={\frac {1}{2}}(\delta (t+1)+\delta (t-1)).$$

More generally, if a discrete variable can takendifferent values among real numbers, then the associated probability density function is: $$f(t)=\sum _{i=1}^{n}p_{i}\,\delta (t-x_{i}),$$ where$x_{1},\ldots,x_{n}$are the discrete values accessible to the variable and$p_{1},\ldots,p_{n}$are the probabilities associated with these values.

This substantially unifies the treatment of discrete and continuous probability distributions. The above expression allows for determining statistical characteristics of such a discrete variable (such as themean,variance,andkurtosis), starting from the formulas given for a continuous distribution of the probability.

Families of densities

It is common for probability density functions (andprobability mass functions) to be parametrized—that is, to be characterized by unspecifiedparameters.For example, thenormal distributionis parametrized in terms of themeanand thevariance,denoted by$\mu$and$\sigma ^{2}$respectively, giving the family of densities $$f(x;\mu,\sigma ^{2})={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}.$$ Different values of the parameters describe different distributions of differentrandom variableson the samesample space(the same set of all possible values of the variable); this sample space is the domain of the family of random variables that this family of distributions describes. A given set of parameters describes a single distribution within the family sharing the functional form of the density. From the perspective of a given distribution, the parameters are constants, and terms in a density function that contain only parameters, but not variables, are part of thenormalization factorof a distribution (the multiplicative factor that ensures that the area under the density—the probability ofsomethingin the domain occurring— equals 1). This normalization factor is outside thekernelof the distribution.

Since the parameters are constants, reparametrizing a density in terms of different parameters to give a characterization of a different random variable in the family, means simply substituting the new parameter values into the formula in place of the old ones.

Densities associated with multiple variables

For continuousrandom variablesX₁,...,X_n,it is also possible to define a probability density function associated to the set as a whole, often calledjoint probability density function.This density function is defined as a function of thenvariables, such that, for any domainDin then-dimensional space of the values of the variablesX₁,...,X_n,the probability that a realisation of the set variables falls inside the domainDis $$\Pr \left(X_{1},\ldots,X_{n}\in D\right)=\int _{D}f_{X_{1},\ldots,X_{n}}(x_{1},\ldots,x_{n})\,dx_{1}\cdots dx_{n}.$$

IfF(x₁,...,x_n) = Pr(X₁≤x₁,...,X_n≤x_n)is thecumulative distribution functionof the vector(X₁,...,X_n),then the joint probability density function can be computed as a partial derivative $$f(x)=\left.{\frac {\partial ^{n}F}{\partial x_{1}\cdots \partial x_{n}}}\right|_{x}$$

Marginal densities

Fori= 1, 2,...,n,letf_Xi(x_i)be the probability density function associated with variableX_ialone. This is called the marginal density function, and can be deduced from the probability density associated with the random variablesX₁,...,X_nby integrating over all values of the othern− 1variables: $$f_{X_{i}}(x_{i})=\int f(x_{1},\ldots,x_{n})\,dx_{1}\cdots dx_{i-1}\,dx_{i+1}\cdots dx_{n}.$$

Independence

Continuous random variablesX₁,...,X_nadmitting a joint density are allindependentfrom each other if and only if $$f_{X_{1},\ldots,X_{n}}(x_{1},\ldots,x_{n})=f_{X_{1}}(x_{1})\cdots f_{X_{n}}(x_{n}).$$

Corollary

If the joint probability density function of a vector ofnrandom variables can be factored into a product ofnfunctions of one variable $$f_{X_{1},\ldots,X_{n}}(x_{1},\ldots,x_{n})=f_{1}(x_{1})\cdots f_{n}(x_{n}),$$ (where eachf_iis not necessarily a density) then thenvariables in the set are allindependentfrom each other, and the marginal probability density function of each of them is given by $$f_{X_{i}}(x_{i})={\frac {f_{i}(x_{i})}{\int f_{i}(x)\,dx}}.$$

Example

This elementary example illustrates the above definition of multidimensional probability density functions in the simple case of a function of a set of two variables. Let us call${\vec {R}}$a 2-dimensional random vector of coordinates(X,Y):the probability to obtain${\vec {R}}$in the quarter plane of positivexandyis $$\Pr \left(X>0,Y>0\right)=\int _{0}^{\infty }\int _{0}^{\infty }f_{X,Y}(x,y)\,dx\,dy.$$

Function of random variables and change of variables in the probability density function

If the probability density function of a random variable (or vector)Xis given asf_X(x),it is possible (but often not necessary; see below) to calculate the probability density function of some variableY=g(X).This is also called a "change of variable" and is in practice used to generate a random variable of arbitrary shapef_g(X)=f_Yusing a known (for instance, uniform) random number generator.

It is tempting to think that in order to find the expected valueE(g(X)),one must first find the probability densityf_g(X)of the new random variableY=g(X).However, rather than computing $$\operatorname {E} {\big (}g(X){\big )}=\int _{-\infty }^{\infty }yf_{g(X)}(y)\,dy,$$ one may find instead $$\operatorname {E} {\big (}g(X){\big )}=\int _{-\infty }^{\infty }g(x)f_{X}(x)\,dx.$$

The values of the two integrals are the same in all cases in which bothXandg(X)actually have probability density functions. It is not necessary thatgbe aone-to-one function.In some cases the latter integral is computed much more easily than the former. SeeLaw of the unconscious statistician.

Scalar to scalar

Let$g:\mathbb {R} \to \mathbb {R}$be amonotonic function,then the resulting density function is $$f_{Y}(y)=f_{X}{\big (}g^{-1}(y){\big )}\left|{\frac {d}{dy}}{\big (}g^{-1}(y){\big )}\right|.$$

Hereg⁻¹denotes theinverse function.

This follows from the fact that the probability contained in a differential area must be invariant under change of variables. That is, $$\left|f_{Y}(y)\,dy\right|=\left|f_{X}(x)\,dx\right|,$$ or $$f_{Y}(y)=\left|{\frac {dx}{dy}}\right|f_{X}(x)=\left|{\frac {d}{dy}}(x)\right|f_{X}(x)=\left|{\frac {d}{dy}}{\big (}g^{-1}(y){\big )}\right|f_{X}{\big (}g^{-1}(y){\big )}={\left|\left(g^{-1}\right)'(y)\right|}\cdot f_{X}{\big (}g^{-1}(y){\big )}.$$

For functions that are not monotonic, the probability density function foryis $$\sum _{k=1}^{n(y)}\left|{\frac {d}{dy}}g_{k}^{-1}(y)\right|\cdot f_{X}{\big (}g_{k}^{-1}(y){\big )},$$ wheren(y)is the number of solutions inxfor the equation$g(x)=y$,and$g_{k}^{-1}(y)$are these solutions.

Vector to vector

Supposexis ann-dimensional random variable with joint densityf.Ify=G(x),whereGis abijective,differentiable function,thenyhas densityp_Y: $$p_{Y}(\mathbf {y} )=f{\Bigl (}G^{-1}(\mathbf {y} ){\Bigr )}\left|\det \left[\left.{\frac {dG^{-1}(\mathbf {z} )}{d\mathbf {z} }}\right|_{\mathbf {z} =\mathbf {y} }\right]\right|$$ with the differential regarded as theJacobianof the inverse ofG(⋅),evaluated aty.

For example, in the 2-dimensional casex= (x₁,x₂),suppose the transformGis given asy₁=G₁(x₁,x₂),y₂=G₂(x₁,x₂)with inversesx₁=G₁⁻¹(y₁,y₂),x₂=G₂⁻¹(y₁,y₂).The joint distribution fory= (y₁,y₂) has density $$p_{Y_{1},Y_{2}}(y_{1},y_{2})=f_{X_{1},X_{2}}{\big (}G_{1}^{-1}(y_{1},y_{2}),G_{2}^{-1}(y_{1},y_{2}){\big )}\left\vert {\frac {\partial G_{1}^{-1}}{\partial y_{1}}}{\frac {\partial G_{2}^{-1}}{\partial y_{2}}}-{\frac {\partial G_{1}^{-1}}{\partial y_{2}}}{\frac {\partial G_{2}^{-1}}{\partial y_{1}}}\right\vert.$$

Vector to scalar

Let$V:\mathbb {R} ^{n}\to \mathbb {R}$be a differentiable function and$X$be a random vector taking values in$\mathbb {R} ^{n}$,$f_{X}$be the probability density function of$X$and$\delta (\cdot )$be theDirac deltafunction. It is possible to use the formulas above to determine$f_{Y}$,the probability density function of$Y=V(X)$,which will be given by $$f_{Y}(y)=\int _{\mathbb {R} ^{n}}f_{X}(\mathbf {x} )\delta {\big (}y-V(\mathbf {x} ){\big )}\,d\mathbf {x}.$$

This result leads to thelaw of the unconscious statistician: $$\operatorname {E} _{Y}[Y]=\int _{\mathbb {R} }yf_{Y}(y)\,dy=\int _{\mathbb {R} }y\int _{\mathbb {R} ^{n}}f_{X}(\mathbf {x} )\delta {\big (}y-V(\mathbf {x} ){\big )}\,d\mathbf {x} \,dy=\int _{{\mathbb {R} }^{n}}\int _{\mathbb {R} }yf_{X}(\mathbf {x} )\delta {\big (}y-V(\mathbf {x} ){\big )}\,dy\,d\mathbf {x} =\int _{\mathbb {R} ^{n}}V(\mathbf {x} )f_{X}(\mathbf {x} )\,d\mathbf {x} =\operatorname {E} _{X}[V(X)].$$

Proof:

Let$Z$be a collapsed random variable with probability density function$p_{Z}(z)=\delta (z)$(i.e., a constant equal to zero). Let the random vector${\tilde {X}}$and the transform$H$be defined as $$H(Z,X)={\begin{bmatrix}Z+V(X)\\X\end{bmatrix}}={\begin{bmatrix}Y\\{\tilde {X}}\end{bmatrix}}.$$

It is clear that$H$is a bijective mapping, and the Jacobian of$H^{-1}$is given by: $${\frac {dH^{-1}(y,{\tilde {\mathbf {x} }})}{dy\,d{\tilde {\mathbf {x} }}}}={\begin{bmatrix}1&-{\frac {dV({\tilde {\mathbf {x} }})}{d{\tilde {\mathbf {x} }}}}\\\mathbf {0} _{n\times 1}&\mathbf {I} _{n\times n}\end{bmatrix}},$$ which is an upper triangular matrix with ones on the main diagonal, therefore its determinant is 1. Applying the change of variable theorem from the previous section we obtain that $$f_{Y,X}(y,x)=f_{X}(\mathbf {x} )\delta {\big (}y-V(\mathbf {x} ){\big )},$$ which if marginalized over$x$leads to the desired probability density function.

Sums of independent random variables

See also:List of convolutions of probability distributions

The probability density function of the sum of twoindependentrandom variablesUandV,each of which has a probability density function, is theconvolutionof their separate density functions: $$f_{U+V}(x)=\int _{-\infty }^{x}f_{U}(y)f_{V}(x-y)\,dy=\left(f_{U}*f_{V}\right)(x)$$

It is possible to generalize the previous relation to a sum of N independent random variables, with densitiesU₁,...,U_N: $$f_{U_{1}+\cdots +U}(x)=\left(f_{U_{1}}*\cdots *f_{U_{N}}\right)(x)$$

This can be derived from a two-way change of variables involvingY=U+VandZ=V,similarly to the example below for the quotient of independent random variables.

Products and quotients of independent random variables

See also:Product distributionandRatio distribution

Given two independent random variablesUandV,each of which has a probability density function, the density of the productY=UVand quotientY=U/Vcan be computed by a change of variables.

Example: Quotient distribution

To compute the quotientY=U/Vof two independent random variablesUandV,define the following transformation: $${\begin{aligned}Y&=U/V\\[1ex]Z&=V\end{aligned}}$$

Then, the joint densityp(y,z)can be computed by a change of variables fromU,VtoY,Z,andYcan be derived bymarginalizing outZfrom the joint density.

The inverse transformation is $${\begin{aligned}U&=YZ\\V&=Z\end{aligned}}$$

The absolute value of theJacobian matrixdeterminant$J(U,V\mid Y,Z)$of this transformation is: $$\left|\det {\begin{bmatrix}{\frac {\partial u}{\partial y}}&{\frac {\partial u}{\partial z}}\\{\frac {\partial v}{\partial y}}&{\frac {\partial v}{\partial z}}\end{bmatrix}}\right|=\left|\det {\begin{bmatrix}z&y\\0&1\end{bmatrix}}\right|=|z|.$$

Thus: $$p(y,z)=p(u,v)\,J(u,v\mid y,z)=p(u)\,p(v)\,J(u,v\mid y,z)=p_{U}(yz)\,p_{V}(z)\,|z|.$$

And the distribution ofYcan be computed bymarginalizing outZ: $$p(y)=\int _{-\infty }^{\infty }p_{U}(yz)\,p_{V}(z)\,|z|\,dz$$

This method crucially requires that the transformation fromU,VtoY,Zbebijective.The above transformation meets this becauseZcan be mapped directly back toV,and for a givenVthe quotientU/Vismonotonic.This is similarly the case for the sumU+V,differenceU−Vand productUV.

Exactly the same method can be used to compute the distribution of other functions of multiple independent random variables.

Example: Quotient of two standard normals

Given twostandard normalvariablesUandV,the quotient can be computed as follows. First, the variables have the following density functions: $${\begin{aligned}p(u)&={\frac {1}{\sqrt {2\pi }}}e^{-{u^{2}}/{2}}\\[1ex]p(v)&={\frac {1}{\sqrt {2\pi }}}e^{-{v^{2}}/{2}}\end{aligned}}$$

We transform as described above: $${\begin{aligned}Y&=U/V\\[1ex]Z&=V\end{aligned}}$$

This leads to: $${\begin{aligned}p(y)&=\int _{-\infty }^{\infty }p_{U}(yz)\,p_{V}(z)\,|z|\,dz\\[5pt]&=\int _{-\infty }^{\infty }{\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}y^{2}z^{2}}{\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}z^{2}}|z|\,dz\\[5pt]&=\int _{-\infty }^{\infty }{\frac {1}{2\pi }}e^{-{\frac {1}{2}}\left(y^{2}+1\right)z^{2}}|z|\,dz\\[5pt]&=2\int _{0}^{\infty }{\frac {1}{2\pi }}e^{-{\frac {1}{2}}\left(y^{2}+1\right)z^{2}}z\,dz\\[5pt]&=\int _{0}^{\infty }{\frac {1}{\pi }}e^{-\left(y^{2}+1\right)u}\,du&&u={\tfrac {1}{2}}z^{2}\\[5pt]&=\left.-{\frac {1}{\pi \left(y^{2}+1\right)}}e^{-\left(y^{2}+1\right)u}\right|_{u=0}^{\infty }\\[5pt]&={\frac {1}{\pi \left(y^{2}+1\right)}}\end{aligned}}$$

This is the density of a standardCauchy distribution.

See also

• Density estimation– Estimate of an unobservable underlying probability density function
• Kernel density estimation– EstimatorPages displaying short descriptions with no spaces
• Likelihood function– Function related to statistics and probability theory
• List of probability distributions
• Probability amplitude– Complex number whose squared absolute value is a probability
• Probability mass function– Discrete-variable probability distribution
• Secondary measure
• Uses asposition probability density:
  • Atomic orbital– Function describing an electron in an atom
  • Home range– The area in which an animal lives and moves on a periodic basis

Further reading

• Billingsley, Patrick(1979).Probability and Measure.New York, Toronto, London: John Wiley and Sons.ISBN0-471-00710-2.
• Casella, George;Berger, Roger L.(2002).Statistical Inference(Second ed.). Thomson Learning. pp. 34–37.ISBN0-534-24312-6.
• Stirzaker, David (2003).Elementary Probability.Cambridge University Press.ISBN0-521-42028-8.Chapters 7 to 9 are about continuous variables.

External links

• Ushakov, N.G. (2001) [1994],"Density of a probability distribution",Encyclopedia of Mathematics,EMS Press
• Weisstein, Eric W."Probability density function".MathWorld.