Quantum group

Inmathematicsandtheoretical physics,the termquantum groupdenotes one of a few different kinds ofnoncommutative algebraswith additional structure. These include Drinfeld–Jimbo type quantum groups (which arequasitriangular Hopf algebras),compact matrix quantum groups(which are structures on unital separableC*-algebras), and bicrossproduct quantum groups. Despite their name, they do not themselves have a natural group structure, though they are in some sense 'close' to a group.

The term "quantum group" first appeared in the theory ofquantum integrable systems,which was then formalized byVladimir DrinfeldandMichio Jimboas a particular class ofHopf algebra.The same term is also used for other Hopf algebras that deform or are close to classicalLie groupsorLie algebras,such as a "bicrossproduct" class of quantum groups introduced byShahn Majida little after the work of Drinfeld and Jimbo.

In Drinfeld's approach, quantum groups arise asHopf algebrasdepending on an auxiliary parameterqorh,which becomeuniversal enveloping algebrasof a certain Lie algebra, frequentlysemisimpleoraffine,whenq= 1 orh= 0. Closely related are certain dual objects, also Hopf algebras and also called quantum groups, deforming the algebra of functions on the corresponding semisimplealgebraic groupor acompact Lie group.

Intuitive meaning

The discovery of quantum groups was quite unexpected since it was known for a long time thatcompact groupsand semisimple Lie algebras are "rigid" objects, in other words, they cannot be "deformed". One of the ideas behind quantum groups is that if we consider a structure that is in a sense equivalent but larger, namely agroup algebraor auniversal enveloping algebra,then a group algebra or enveloping algebra can be "deformed", although the deformation will no longer remain a group algebra or enveloping algebra. More precisely, deformation can be accomplished within the category ofHopf algebrasthat are not required to be eithercommutativeorcocommutative.One can think of the deformed object as an algebra of functions on a "noncommutative space", in the spirit of thenoncommutative geometryofAlain Connes.This intuition, however, came after particular classes of quantum groups had already proved their usefulness in the study of the quantumYang–Baxter equationandquantum inverse scattering methoddeveloped by the Leningrad School (Ludwig Faddeev,Leon Takhtajan,Evgeny Sklyanin,Nicolai ReshetikhinandVladimir Korepin) and related work by the Japanese School.The intuition behind the second,bicrossproduct,class of quantum groups was different and came from the search for self-dual objects as an approach toquantum gravity.

Drinfeld–Jimbo type quantum groups

One type of objects commonly called a "quantum group" appeared in the work of Vladimir Drinfeld and Michio Jimbo as a deformation of theuniversal enveloping algebraof asemisimple Lie algebraor, more generally, aKac–Moody algebra,in the category ofHopf algebras.The resulting algebra has additional structure, making it into aquasitriangular Hopf algebra.

LetA= (a_ij) be theCartan matrixof the Kac–Moody algebra, and letq≠ 0, 1 be a complex number, then the quantum group,U_q(G), whereGis the Lie algebra whose Cartan matrix isA,is defined as theunitalassociative algebrawith generatorsk_λ(whereλis an element of theweight lattice,i.e. 2(λ, α_i)/(α_i,α_i) is an integer for alli), ande_iandf_i(forsimple roots,α_i), subject to the following relations:

${\begin{aligned}k_{0}&=1\\k_{\lambda }k_{\mu }&=k_{\lambda +\mu }\\k_{\lambda }e_{i}k_{\lambda }^{-1}&=q^{(\lambda,\alpha _{i})}e_{i}\\k_{\lambda }f_{i}k_{\lambda }^{-1}&=q^{-(\lambda,\alpha _{i})}f_{i}\\\left[e_{i},f_{j}\right]&=\delta _{ij}{\frac {k_{i}-k_{i}^{-1}}{q_{i}-q_{i}^{-1}}}&&k_{i}=k_{\alpha _{i}},q_{i}=q^{{\frac {1}{2}}(\alpha _{i},\alpha _{i})}\\\end{aligned}}$

And fori≠jwe have theq-Serre relations, which are deformations of theSerrerelations:

${\begin{aligned}\sum _{n=0}^{1-a_{ij}}(-1)^{n}{\frac {[1-a_{ij}]_{q_{i}}!}{[1-a_{ij}-n]_{q_{i}}![n]_{q_{i}}!}}e_{i}^{n}e_{j}e_{i}^{1-a_{ij}-n}&=0\\[6pt]\sum _{n=0}^{1-a_{ij}}(-1)^{n}{\frac {[1-a_{ij}]_{q_{i}}!}{[1-a_{ij}-n]_{q_{i}}![n]_{q_{i}}!}}f_{i}^{n}f_{j}f_{i}^{1-a_{ij}-n}&=0\end{aligned}}$

where theq-factorial,theq-analogof the ordinaryfactorial,is defined recursively using q-number:

${\begin{aligned}{[0]}_{q_{i}}!&=1\\{[n]}_{q_{i}}!&=\prod _{m=1}^{n}[m]_{q_{i}},&&[m]_{q_{i}}={\frac {q_{i}^{m}-q_{i}^{-m}}{q_{i}-q_{i}^{-1}}}\end{aligned}}$

In the limit asq→ 1, these relations approach the relations for the universal enveloping algebraU(G), where

$k_{\lambda }\to 1,\qquad {\frac {k_{\lambda }-k_{-\lambda }}{q-q^{-1}}}\to t_{\lambda }$

andt_λis the element of the Cartan subalgebra satisfying (t_λ,h) =λ(h) for allhin the Cartan subalgebra.

There are variouscoassociative coproductsunder which these algebras are Hopf algebras, for example,

${\begin{array}{lll}\Delta _{1}(k_{\lambda })=k_{\lambda }\otimes k_{\lambda }&\Delta _{1}(e_{i})=1\otimes e_{i}+e_{i}\otimes k_{i}&\Delta _{1}(f_{i})=k_{i}^{-1}\otimes f_{i}+f_{i}\otimes 1\\\Delta _{2}(k_{\lambda })=k_{\lambda }\otimes k_{\lambda }&\Delta _{2}(e_{i})=k_{i}^{-1}\otimes e_{i}+e_{i}\otimes 1&\Delta _{2}(f_{i})=1\otimes f_{i}+f_{i}\otimes k_{i}\\\Delta _{3}(k_{\lambda })=k_{\lambda }\otimes k_{\lambda }&\Delta _{3}(e_{i})=k_{i}^{-{\frac {1}{2}}}\otimes e_{i}+e_{i}\otimes k_{i}^{\frac {1}{2}}&\Delta _{3}(f_{i})=k_{i}^{-{\frac {1}{2}}}\otimes f_{i}+f_{i}\otimes k_{i}^{\frac {1}{2}}\end{array}}$

where the set of generators has been extended, if required, to includek_λforλwhich is expressible as the sum of an element of the weight lattice and half an element of theroot lattice.

In addition, any Hopf algebra leads to another with reversed coproductToΔ, whereTis given byT(x⊗y) =y⊗x,giving three more possible versions.

ThecounitonU_q(A) is the same for all these coproducts:ε(k_λ) = 1,ε(e_i) =ε(f_i) = 0, and the respectiveantipodesfor the above coproducts are given by

${\begin{array}{lll}S_{1}(k_{\lambda })=k_{-\lambda }&S_{1}(e_{i})=-e_{i}k_{i}^{-1}&S_{1}(f_{i})=-k_{i}f_{i}\\S_{2}(k_{\lambda })=k_{-\lambda }&S_{2}(e_{i})=-k_{i}e_{i}&S_{2}(f_{i})=-f_{i}k_{i}^{-1}\\S_{3}(k_{\lambda })=k_{-\lambda }&S_{3}(e_{i})=-q_{i}e_{i}&S_{3}(f_{i})=-q_{i}^{-1}f_{i}\end{array}}$

Alternatively, the quantum groupU_q(G) can be regarded as an algebra over the fieldC(q), the field of allrational functionsof an indeterminateqoverC.

Similarly, the quantum groupU_q(G) can be regarded as an algebra over the fieldQ(q), the field of allrational functionsof an indeterminateqoverQ(see below in the section on quantum groups atq= 0). The center of quantum group can be described by quantum determinant.

Representation theory

Just as there are many different types of representations for Kac–Moody algebras and their universal enveloping algebras, so there are many different types of representation for quantum groups.

As is the case for all Hopf algebras,U_q(G) has anadjoint representationon itself as a module, with the action being given by

$\mathrm {Ad} _{x}\cdot y=\sum _{(x)}x_{(1)}yS(x_{(2)}),$

where

$\Delta (x)=\sum _{(x)}x_{(1)}\otimes x_{(2)}.$

Case 1:qis not a root of unity

One important type of representation is a weight representation, and the correspondingmoduleis called a weight module. A weight module is a module with a basis of weight vectors. A weight vector is a nonzero vectorvsuch thatk_λ·v=d_λvfor allλ,whered_λare complex numbers for all weightsλsuch that

$d_{0}=1,$

$d_{\lambda }d_{\mu }=d_{\lambda +\mu },$for all weightsλandμ.

A weight module is called integrable if the actions ofe_iandf_iare locally nilpotent (i.e. for any vectorvin the module, there exists a positive integerk,possibly dependent onv,such that$e_{i}^{k}.v=f_{i}^{k}.v=0$for alli). In the case of integrable modules, the complex numbersd_λassociated with a weight vector satisfy$d_{\lambda }=c_{\lambda }q^{(\lambda,\nu )}$,whereνis an element of the weight lattice, andc_λare complex numbers such that

• $c_{0}=1,$
• $c_{\lambda }c_{\mu }=c_{\lambda +\mu },$for all weightsλandμ,
• $c_{2\alpha _{i}}=1$for alli.

Of special interest arehighest-weight representations,and the corresponding highest weight modules. A highest weight module is a module generated by a weight vectorv,subject tok_λ·v=d_λvfor all weightsμ,ande_i·v= 0 for alli.Similarly, a quantum group can have a lowest weight representation and lowest weight module,i.e.a module generated by a weight vectorv,subject tok_λ·v=d_λvfor all weightsλ,andf_i·v= 0 for alli.

Define a vectorvto have weightνif$k_{\lambda }\cdot v=q^{(\lambda,\nu )}v$for allλin the weight lattice.

IfGis a Kac–Moody algebra, then in any irreducible highest weight representation ofU_q(G), with highest weight ν, the multiplicities of the weights are equal to their multiplicities in an irreducible representation ofU(G) with equal highest weight. If the highest weight is dominant and integral (a weightμis dominant and integral ifμsatisfies the condition that$2(\mu,\alpha _{i})/(\alpha _{i},\alpha _{i})$is a non-negative integer for alli), then the weight spectrum of the irreducible representation is invariant under theWeyl groupforG,and the representation is integrable.

Conversely, if a highest weight module is integrable, then its highest weight vectorvsatisfies$k_{\lambda }\cdot v=c_{\lambda }q^{(\lambda,\nu )}v$,wherec_λ·v=d_λvare complex numbers such that

• $c_{0}=1,$
• $c_{\lambda }c_{\mu }=c_{\lambda +\mu },$for all weightsλandμ,
• $c_{2\alpha _{i}}=1$for alli,

andνis dominant and integral.

As is the case for all Hopf algebras, thetensor productof two modules is another module. For an elementxofU_q(G),and for vectorsvandwin the respective modules,x⋅ (v⊗w) = Δ(x) ⋅ (v⊗w), so that$k_{\lambda }\cdot (v\otimes w)=k_{\lambda }\cdot v\otimes k_{\lambda }.w$,and in the case of coproduct Δ₁,$e_{i}\cdot (v\otimes w)=k_{i}\cdot v\otimes e_{i}\cdot w+e_{i}\cdot v\otimes w$and$f_{i}\cdot (v\otimes w)=v\otimes f_{i}\cdot w+f_{i}\cdot v\otimes k_{i}^{-1}\cdot w.$

The integrable highest weight module described above is a tensor product of a one-dimensional module (on whichk_λ=c_λfor allλ,ande_i=f_i= 0 for alli) and a highest weight module generated by a nonzero vectorv₀,subject to$k_{\lambda }\cdot v_{0}=q^{(\lambda,\nu )}v_{0}$for all weightsλ,and$e_{i}\cdot v_{0}=0$for alli.

In the specific case whereGis a finite-dimensional Lie algebra (as a special case of a Kac–Moody algebra), then the irreducible representations with dominant integral highest weights are also finite-dimensional.

In the case of a tensor product of highest weight modules, its decomposition into submodules is the same as for the tensor product of the corresponding modules of the Kac–Moody algebra (the highest weights are the same, as are their multiplicities).

Quasitriangularity

Case 1:qis not a root of unity

Strictly, the quantum groupU_q(G) is not quasitriangular, but it can be thought of as being "nearly quasitriangular" in that there exists an infinite formal sum which plays the role of anR-matrix.This infinite formal sum is expressible in terms of generatorse_iandf_i,and Cartan generatorst_λ,wherek_λis formally identified withq^t_λ.The infinite formal sum is the product of two factors,

$q^{\eta \sum _{j}t_{\lambda _{j}}\otimes t_{\mu _{j}}}$

and an infinite formal sum, whereλ_jis a basis for the dual space to the Cartan subalgebra, andμ_jis the dual basis, andη= ±1.

The formal infinite sum which plays the part of theR-matrixhas a well-defined action on the tensor product of two irreducible highest weight modules, and also on the tensor product of two lowest weight modules. Specifically, ifvhas weightαandwhas weightβ,then

$q^{\eta \sum _{j}t_{\lambda _{j}}\otimes t_{\mu _{j}}}\cdot (v\otimes w)=q^{\eta (\alpha,\beta )}v\otimes w,$

and the fact that the modules are both highest weight modules or both lowest weight modules reduces the action of the other factor onv⊗Wto a finite sum.

Specifically, ifVis a highest weight module, then the formal infinite sum,R,has a well-defined, andinvertible,action onV⊗V,and this value ofR(as an element of End(V⊗V)) satisfies theYang–Baxter equation,and therefore allows us to determine a representation of thebraid group,and to define quasi-invariants forknots,linksandbraids.

Quantum groups atq= 0

Main article:Crystal base

Masaki Kashiwarahas researched the limiting behaviour of quantum groups asq→ 0, and found a particularly well behaved base called acrystal base.

Description and classification by root-systems and Dynkin diagrams

There has been considerable progress in describing finite quotients of quantum groups such as the aboveU_q(g) forqⁿ= 1; one usually considers the class ofpointedHopf algebras,meaning that all simple left or right comodules are 1-dimensional and thus the sum of all its simple subcoalgebras forms a group algebra called thecoradical:

• In 2002 H.-J. Schneider and N. Andruskiewitschfinished their classification of pointed Hopf algebras with an abelian co-radical group (excluding primes 2, 3, 5, 7), especially as the above finite quotients ofU_q(g) decompose intoE′s (Borel part), dualF′s andK′s (Cartan algebra) just like ordinarySemisimple Lie algebras:

$\left({\mathfrak {B}}(V)\otimes k[\mathbf {Z} ^{n}]\otimes {\mathfrak {B}}(V^{*})\right)^{\sigma }$

Here, as in the classical theoryVis abraided vector spaceof dimensionnspanned by theE′s, andσ(a so-called cocycle twist) creates the nontriviallinkingbetweenE′s andF′s. Note that in contrast to classical theory, more than two linked components may appear. The role of thequantum Borel algebrais taken by aNichols algebra${\mathfrak {B}}(V)$of the braided vectorspace.

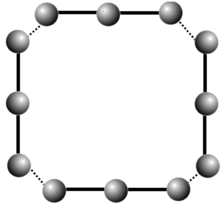
generalized Dynkin diagram for a pointed Hopf algebra linking four A3 copies

• A crucial ingredient was I. Heckenberger'sclassification of finite Nichols algebrasfor abelian groups in terms of generalizedDynkin diagrams.When small primes are present, some exotic examples, such as a triangle, occur (see also the Figure of a rank 3 Dankin diagram).

A rank 3 Dynkin diagram associated to a finite-dimensional Nichols algebra

• Meanwhile, Schneider and Heckenbergerhave generally proven the existence of anarithmeticroot systemalso in the nonabelian case, generating aPBW basisas proven by Kharcheko in the abelian case (without the assumption on finite dimension). This can be usedon specific casesU_q(g) and explains e.g. the numerical coincidence between certain coideal subalgebras of these quantum groups and the order of theWeyl groupof theLie algebrag.

Compact matrix quantum groups

Main article:Compact quantum group

S. L. Woronowiczintroduced compact matrix quantum groups. Compact matrix quantum groups are abstract structures on which the "continuous functions" on the structure are given by elements of aC*-algebra.The geometry of a compact matrix quantum group is a special case of anoncommutative geometry.

The continuous complex-valued functions on a compact Hausdorff topological space form a commutative C*-algebra. By theGelfand theorem,a commutative C*-algebra is isomorphic to the C*-algebra of continuous complex-valued functions on a compact Hausdorff topological space, and the topological space is uniquely determined by the C*-algebra up tohomeomorphism.

For a compacttopological group,G,there exists a C*-algebra homomorphism Δ:C(G) →C(G) ⊗C(G) (whereC(G) ⊗C(G) is the C*-algebra tensor product - the completion of the algebraic tensor product ofC(G) andC(G)), such that Δ(f)(x,y) =f(xy) for allf∈C(G), and for allx,y∈G(where (f⊗g)(x,y) =f(x)g(y) for allf,g∈C(G) and allx,y∈G). There also exists a linear multiplicative mappingκ:C(G) →C(G), such thatκ(f)(x) =f(x⁻¹) for allf∈C(G) and allx∈G.Strictly, this does not makeC(G) a Hopf algebra, unlessGis finite. On the other hand, a finite-dimensionalrepresentationofGcan be used to generate a *-subalgebra ofC(G) which is also a Hopf *-algebra. Specifically, if$g\mapsto (u_{ij}(g))_{i,j}$is ann-dimensional representation ofG,then for alli,ju_ij∈C(G) and

$\Delta (u_{ij})=\sum _{k}u_{ik}\otimes u_{kj}.$

It follows that the *-algebra generated byu_ijfor alli, jandκ(u_ij) for alli, jis a Hopf *-algebra: the counit is determined by ε(u_ij) = δ_ijfor alli, j(whereδ_ijis theKronecker delta), the antipode isκ,and the unit is given by

$1=\sum _{k}u_{1k}\kappa (u_{k1})=\sum _{k}\kappa (u_{1k})u_{k1}.$

General definition

As a generalization, a compact matrix quantum group is defined as a pair (C,u), whereCis a C*-algebra and$u=(u_{ij})_{i,j=1,\dots,n}$is a matrix with entries inCsuch that

• The *-subalgebra,C₀,ofC,which is generated by the matrix elements ofu,is dense inC;

• There exists a C*-algebra homomorphism called the comultiplication Δ:C→C⊗C(whereC⊗Cis the C*-algebra tensor product - the completion of the algebraic tensor product ofCandC) such that for alli, jwe have:

$\Delta (u_{ij})=\sum _{k}u_{ik}\otimes u_{kj}$

• There exists a linear antimultiplicative map κ:C₀→C₀(the coinverse) such thatκ(κ(v*)*) =vfor allv∈C₀and

$\sum _{k}\kappa (u_{ik})u_{kj}=\sum _{k}u_{ik}\kappa (u_{kj})=\delta _{ij}I,$

whereIis the identity element ofC.Since κ is antimultiplicative, thenκ(vw) =κ(w)κ(v) for allv,winC₀.

As a consequence of continuity, the comultiplication onCis coassociative.

In general,Cis not a bialgebra, andC₀is a Hopf *-algebra.

Informally,Ccan be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, anducan be regarded as a finite-dimensional representation of the compact matrix quantum group.

Representations

A representation of the compact matrix quantum group is given by acorepresentationof the Hopf *-algebra (a corepresentation of a counital coassociative coalgebraAis a square matrix$v=(v_{ij})_{i,j=1,\dots,n}$with entries inA(sovbelongs to M(n,A)) such that

$\Delta (v_{ij})=\sum _{k=1}^{n}v_{ik}\otimes v_{kj}$

for alli,jandε(v_ij) = δ_ijfor alli, j). Furthermore, a representationv,is called unitary if the matrix forvis unitary (or equivalently, if κ(v_ij) =v*_ijfor alli,j).

Example

An example of a compact matrix quantum group is SU_μ(2), where the parameter μ is a positive real number. So SU_μ(2) = (C(SU_μ(2)),u), where C(SU_μ(2)) is the C*-algebra generated by α and γ, subject to

$\gamma \gamma ^{*}=\gamma ^{*}\gamma,$

$\alpha \gamma =\mu \gamma \alpha,$

$\alpha \gamma ^{*}=\mu \gamma ^{*}\alpha,$

$\alpha \alpha ^{*}+\mu \gamma ^{*}\gamma =\alpha ^{*}\alpha +\mu ^{-1}\gamma ^{*}\gamma =I,$

and

$u=\left({\begin{matrix}\alpha &\gamma \\-\gamma ^{*}&\alpha ^{*}\end{matrix}}\right),$

so that the comultiplication is determined by ∆(α) = α ⊗ α − γ ⊗ γ*, ∆(γ) = α ⊗ γ + γ ⊗ α*, and the coinverse is determined by κ(α) = α*, κ(γ) = −μ⁻¹γ, κ(γ*) = −μγ*, κ(α*) = α. Note thatuis a representation, but not a unitary representation.uis equivalent to the unitary representation

$v=\left({\begin{matrix}\alpha &{\sqrt {\mu }}\gamma \\-{\frac {1}{\sqrt {\mu }}}\gamma ^{*}&\alpha ^{*}\end{matrix}}\right).$

Equivalently, SU_μ(2) = (C(SU_μ(2)),w), where C(SU_μ(2)) is the C*-algebra generated by α and β, subject to

$\beta \beta ^{*}=\beta ^{*}\beta,$

$\alpha \beta =\mu \beta \alpha,$

$\alpha \beta ^{*}=\mu \beta ^{*}\alpha,$

$\alpha \alpha ^{*}+\mu ^{2}\beta ^{*}\beta =\alpha ^{*}\alpha +\beta ^{*}\beta =I,$

and

$w=\left({\begin{matrix}\alpha &\mu \beta \\-\beta ^{*}&\alpha ^{*}\end{matrix}}\right),$

so that the comultiplication is determined by ∆(α) = α ⊗ α − μβ ⊗ β*, Δ(β) = α ⊗ β + β ⊗ α*, and the coinverse is determined by κ(α) = α*, κ(β) = −μ⁻¹β, κ(β*) = −μβ*, κ(α*) = α. Note thatwis a unitary representation. The realizations can be identified by equating$\gamma ={\sqrt {\mu }}\beta$.

When μ = 1, then SU_μ(2) is equal to the algebraC(SU(2)) of functions on the concrete compact group SU(2).

Bicrossproduct quantum groups

Whereas compact matrix pseudogroups are typically versions of Drinfeld-Jimbo quantum groups in a dual function algebra formulation, with additional structure, the bicrossproduct ones are a distinct second family of quantum groups of increasing importance as deformations of solvable rather than semisimple Lie groups. They are associated to Lie splittings of Lie algebras or local factorisations of Lie groups and can be viewed as the cross product or Mackey quantisation of one of the factors acting on the other for the algebra and a similar story for the coproduct Δ with the second factor acting back on the first.

The very simplest nontrivial example corresponds to two copies ofRlocally acting on each other and results in a quantum group (given here in an algebraic form) with generatorsp,K,K⁻¹,say, and coproduct

$[p,K]=hK(K-1)$

$\Delta p=p\otimes K+1\otimes p$

$\Delta K=K\otimes K$

wherehis the deformation parameter.

This quantum group was linked to a toy model of Planck scale physics implementingBorn reciprocitywhen viewed as a deformation of theHeisenberg algebraof quantum mechanics. Also, starting with any compact real form of a semisimple Lie algebragits complexification as a real Lie algebra of twice the dimension splits intogand a certain solvable Lie algebra (theIwasawa decomposition), and this provides a canonical bicrossproduct quantum group associated tog.Forsu(2) one obtains a quantum group deformation of theEuclidean groupE(3) of motions in 3 dimensions.

See also

• Hopf algebra
• Lie bialgebra
• Poisson–Lie group
• Quantum affine algebra

References

• Grensing, Gerhard (2013).Structural Aspects of Quantum Field Theory and Noncommutative Geometry.World Scientific.doi:10.1142/8771.ISBN978-981-4472-69-2.
• Jagannathan, R.(2001). "Some introductory notes on quantum groups, quantum algebras, and their applications".arXiv:math-ph/0105002.
• Kassel, Christian (1995),Quantum groups,Graduate Texts in Mathematics, vol. 155, Berlin, New York: Springer-Verlag,doi:10.1007/978-1-4612-0783-2,ISBN978-0-387-94370-1,MR1321145
• Lusztig, George (2010) [1993].Introduction to Quantum Groups.Cambridge, MA: Birkhäuser.ISBN978-0-817-64716-2.
• Majid, Shahn (2002),A quantum groups primer,London Mathematical Society Lecture Note Series, vol. 292, Cambridge University Press,doi:10.1017/CBO9780511549892,ISBN978-0-521-01041-2,MR1904789
• Majid, Shahn (January 2006),"What Is...a Quantum Group?"(PDF),Notices of the American Mathematical Society,53(1): 30–31,retrieved2008-01-16
• Podles, P.; Muller, E. (1998), "Introduction to quantum groups",Reviews in Mathematical Physics,10(4): 511–551,arXiv:q-alg/9704002,Bibcode:1998RvMaP..10..511P,doi:10.1142/S0129055X98000173,S2CID2596718
• Shnider, Steven;Sternberg, Shlomo (1993).Quantum groups: From coalgebras to Drinfeld algebras.Graduate Texts in Mathematical Physics. Vol. 2. Cambridge, MA: International Press.
• Street, Ross(2007),Quantum groups,Australian Mathematical Society Lecture Series, vol. 19, Cambridge University Press,doi:10.1017/CBO9780511618505,ISBN978-0-521-69524-4,MR2294803