RC circuit

Aresistor–capacitor circuit(RC circuit), orRC filterorRC network,is anelectric circuitcomposed ofresistorsandcapacitors.It may be driven by avoltageorcurrent sourceand these will produce different responses. A first order RC circuit is composed of one resistor and one capacitor and is the simplest type of RC circuit.

RC circuits can be used to filter a signal by blocking certain frequencies and passing others. The two most common RC filters are thehigh-pass filtersandlow-pass filters;band-pass filtersandband-stop filtersusually requireRLC filters,though crude ones can be made with RC filters.

Introduction

There are three basic, linear passivelumpedanalog circuitcomponents: the resistor (R), the capacitor (C), and theinductor(L). These may be combined in the RC circuit, theRL circuit,theLC circuit,and theRLC circuit,with the acronyms indicating which components are used. These circuits, among them, exhibit a large number of important types of behaviour that are fundamental to much ofanalog electronics.In particular, they are able to act aspassive filters.This article considers the RC circuit, in bothseriesandparallelforms, as shown in the diagrams below.

Natural response

RC circuit

The simplest RC circuit consists of a resistor and a charged capacitor connected to one another in a single loop, without an external voltage source. Once the circuit is closed, the capacitor begins to discharge its stored energy through the resistor. The voltage across the capacitor, which is time-dependent, can be found by usingKirchhoff's current law.The current through the resistor must be equal in magnitude (but opposite in sign) to the time derivative of the accumulated charge on the capacitor. This results in thelinear differential equation

$C{\frac {dV}{dt}}+{\frac {V}{R}}=0\,,$

whereCis the capacitance of the capacitor.

Solving this equation forVyields the formula forexponential decay:

$V(t)=V_{0}e^{-{\frac {t}{RC}}}\,,$

whereV₀is the capacitor voltage at timet= 0.

The time required for the voltage to fall to⁠V₀/e⁠is called theRC time constantand is given by,

$\tau =RC\,.$

In this formula,τis measured in seconds,Rin ohms andCin farads.

Complex impedance

Thecomplex impedance,Z_C(inohms) of a capacitor with capacitanceC(infarads) is

$Z_{C}={\frac {1}{sC}}$

Thecomplex frequencysis, in general, acomplex number,

$s=\sigma +j\omega \,,$

where

• jrepresents theimaginary unit:j²= −1,
• σis theexponential decayconstant (innepersper second), and
• ωis thesinusoidalangular frequency(inradians per second).

Sinusoidal steady state

Sinusoidal steady state is a special case in which the input voltage consists of a pure sinusoid (with no exponential decay). As a result,$\sigma =0$and the impedance becomes

$Z_{C}={\frac {1}{j\omega C}}=-{\frac {j}{\omega C}}\,.$

Series circuit

SeriesRC circuit

By viewing the circuit as avoltage divider,thevoltageacross the capacitor is:

$V_{C}(s)={\frac {\frac {1}{Cs}}{R+{\frac {1}{Cs}}}}V_{\mathrm {in} }(s)={\frac {1}{1+RCs}}V_{\mathrm {in} }(s)$

and the voltage across the resistor is:

$V_{R}(s)={\frac {R}{R+{\frac {1}{Cs}}}}V_{\mathrm {in} }(s)={\frac {RCs}{1+RCs}}V_{\mathrm {in} }(s)\,.$

Transfer functions

Thetransfer functionfrom the input voltage to the voltage across the capacitor is

$H_{C}(s)={\frac {V_{C}(s)}{V_{\mathrm {in} }(s)}}={\frac {1}{1+RCs}}\,.$

Similarly, the transfer function from the input to the voltage across the resistor is

$H_{R}(s)={\frac {V_{R}(s)}{V_{\rm {in}}(s)}}={\frac {RCs}{1+RCs}}\,.$

Poles and zeros

Both transfer functions have a singlepolelocated at

$s=-{\frac {1}{RC}}\,.$

In addition, the transfer function for the voltage across the resistor has azerolocated at theorigin.

Gain and phase

Amplitude and phase transfer functions for a series RC circuit

The magnitude of the gains across the two components are

$G_{C}={\big |}H_{C}(j\omega ){\big |}=\left|{\frac {V_{C}(j\omega )}{V_{\mathrm {in} }(j\omega )}}\right|={\frac {1}{\sqrt {1+\left(\omega RC\right)^{2}}}}$

and

$G_{R}={\big |}H_{R}(j\omega ){\big |}=\left|{\frac {V_{R}(j\omega )}{V_{\mathrm {in} }(j\omega )}}\right|={\frac {\omega RC}{\sqrt {1+\left(\omega RC\right)^{2}}}}\,,$

and the phase angles are

$\phi _{C}=\angle H_{C}(j\omega )=\tan ^{-1}\left(-\omega RC\right)$

and

$\phi _{R}=\angle H_{R}(j\omega )=\tan ^{-1}\left({\frac {1}{\omega RC}}\right)\,.$

These expressions together may be substituted into the usual expression for thephasorrepresenting the output:

${\begin{aligned}V_{C}&=G_{C}V_{\mathrm {in} }e^{j\phi _{C}}\\V_{R}&=G_{R}V_{\mathrm {in} }e^{j\phi _{R}}\,.\end{aligned}}$

Current

The current in the circuit is the same everywhere since the circuit is in series:

$I(s)={\frac {V_{\mathrm {in} }(s)}{R+{\frac {1}{Cs}}}}={\frac {Cs}{1+RCs}}V_{\mathrm {in} }(s)\,.$

Impulse response

The impulse response of a series RC circuit

Theimpulse responsefor each voltage is the inverseLaplace transformof the corresponding transfer function. It represents the response of the circuit to an input voltage consisting of an impulse orDirac delta function.

The impulse response for the capacitor voltage is

$h_{C}(t)={\frac {1}{RC}}e^{-{\frac {t}{RC}}}u(t)={\frac {1}{\tau }}e^{-{\frac {t}{\tau }}}u(t)\,,$

whereu(t)is theHeaviside step functionandτ=RCis thetime constant.

Similarly, the impulse response for the resistor voltage is

$h_{R}(t)=\delta (t)-{\frac {1}{RC}}e^{-{\frac {t}{RC}}}u(t)=\delta (t)-{\frac {1}{\tau }}e^{-{\frac {t}{\tau }}}u(t)\,,$

whereδ(t)is theDirac delta function

Frequency-domain considerations

These arefrequency domainexpressions. Analysis of them will show which frequencies the circuits (or filters) pass and reject. This analysis rests on a consideration of what happens to these gains as the frequency becomes very large and very small.

Asω→ ∞:

$G_{C}\to 0\quad {\mbox{and}}\quad G_{R}\to 1\,.$

Asω→ 0:

$G_{C}\to 1\quad {\mbox{and}}\quad G_{R}\to 0\,.$

This shows that, if the output is taken across the capacitor, high frequencies are attenuated (shorted to ground) and low frequencies are passed. Thus, the circuit behaves as alow-pass filter.If, though, the output is taken across the resistor, high frequencies are passed and low frequencies are attenuated (since the capacitor blocks the signal as its frequency approaches 0). In this configuration, the circuit behaves as ahigh-pass filter.

The range of frequencies that the filter passes is called itsbandwidth.The point at which the filter attenuates the signal to half its unfiltered power is termed itscutoff frequency.This requires that the gain of the circuit be reduced to

$G_{C}=G_{R}={\frac {1}{\sqrt {2}}}$.

Solving the above equation yields

$\omega _{\mathrm {c} }={\frac {1}{RC}}\quad {\mbox{or}}\quad f_{\mathrm {c} }={\frac {1}{2\pi RC}}$

which is the frequency that the filter will attenuate to half its original power.

Clearly, the phases also depend on frequency, although this effect is less interesting generally than the gain variations.

Asω→ 0:

$\phi _{C}\to 0\quad {\mbox{and}}\quad \phi _{R}\to 90^{\circ }={\frac {\pi }{2}}{\mbox{ radians}}\,.$

Asω→ ∞:

$\phi _{C}\to -90^{\circ }=-{\frac {\pi }{2}}{\mbox{ radians}}\quad {\mbox{and}}\quad \phi _{R}\to 0\,.$

So atDC(0Hz), the capacitor voltage is in phase with the signal voltage while the resistor voltage leads it by 90°. As frequency increases, the capacitor voltage comes to have a 90° lag relative to the signal and the resistor voltage comes to be in-phase with the signal.

Time-domain considerations

This section relies on knowledge ofe,thenatural logarithmic constant.

The most straightforward way to derive the time domain behaviour is to use theLaplace transformsof the expressions forV_CandV_Rgiven above. This effectively transformsjω→s.Assuming astep input(i.e.V_in= 0beforet= 0and thenV_in=Vafterwards):

${\begin{aligned}V_{\mathrm {in} }(s)&=V\cdot {\frac {1}{s}}\\V_{C}(s)&=V\cdot {\frac {1}{1+sRC}}\cdot {\frac {1}{s}}\\V_{R}(s)&=V\cdot {\frac {sRC}{1+sRC}}\cdot {\frac {1}{s}}\,.\end{aligned}}$

Capacitor voltage step-response.

Resistor voltage step-response.

Partial fractionsexpansions and the inverseLaplace transformyield:

${\begin{aligned}V_{C}(t)&=V\left(1-e^{-{\frac {t}{RC}}}\right)\\V_{R}(t)&=Ve^{-{\frac {t}{RC}}}\,.\end{aligned}}$

These equations are for calculating the voltage across the capacitor and resistor respectively while the capacitor ischarging;for discharging, the equations are vice versa. These equations can be rewritten in terms of charge and current using the relationshipsC=⁠Q/V⁠andV=IR(seeOhm's law).

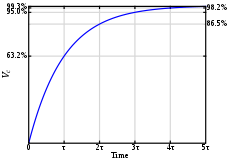
Thus, the voltage across the capacitor tends towardsVas time passes, while the voltage across the resistor tends towards 0, as shown in the figures. This is in keeping with the intuitive point that the capacitor will be charging from the supply voltage as time passes, and will eventually be fully charged.

These equations show that a series RC circuit has atime constant,usually denotedτ=RCbeing the time it takes the voltage across the component to either rise (across the capacitor) or fall (across the resistor) to within⁠1/e⁠of its final value. That is,τis the time it takesV_Cto reachV(1 −⁠1/e⁠)andV_Rto reachV(⁠1/e⁠).

The rate of change is afractional1 −⁠1/e⁠perτ.Thus, in going fromt=Nτtot= (N+ 1)τ,the voltage will have moved about 63.2% of the way from its level att=Nτtoward its final value. So the capacitor will be charged to about 63.2% afterτ,and essentially fully charged (99.3%) after about5τ.When the voltage source is replaced with a short circuit, with the capacitor fully charged, the voltage across the capacitor drops exponentially withtfromVtowards 0. The capacitor will be discharged to about 36.8% afterτ,and essentially fully discharged (0.7%) after about5τ.Note that the current,I,in the circuit behaves as the voltage across the resistor does, viaOhm's Law.

These results may also be derived by solving thedifferential equationsdescribing the circuit:

${\begin{aligned}{\frac {V_{\mathrm {in} }-V_{C}}{R}}&=C{\frac {dV_{C}}{dt}}\\V_{R}&=V_{\mathrm {in} }-V_{C}\,.\end{aligned}}$

The first equation is solved by using anintegrating factorand the second follows easily; the solutions are exactly the same as those obtained via Laplace transforms.

Integrator

Consider the output across the capacitor athighfrequency, i.e.

$\omega \gg {\frac {1}{RC}}\,.$

This means that the capacitor has insufficient time to charge up and so its voltage is very small. Thus the input voltage approximately equals the voltage across the resistor. To see this, consider the expression for$I$given above:

$I={\frac {V_{\mathrm {in} }}{R+{\frac {1}{j\omega C}}}}\,,$

but note that the frequency condition described means that

$\omega C\gg {\frac {1}{R}}\,,$

so

$I\approx {\frac {V_{\mathrm {in} }}{R}}$

which is justOhm's Law.

Now,

$V_{C}={\frac {1}{C}}\int _{0}^{t}I\,dt\,,$

so

$V_{C}\approx {\frac {1}{RC}}\int _{0}^{t}V_{\mathrm {in} }\,dt\,,$

which is anintegratoracross the capacitor.

Differentiator

Consider the output across the resistor atlowfrequency i.e.,

$\omega \ll {\frac {1}{RC}}\,.$

This means that the capacitor has time to charge up until its voltage is almost equal to the source's voltage. Considering the expression forIagain, when

$R\ll {\frac {1}{\omega C}}\,,$

so

${\begin{aligned}I&\approx {\frac {V_{\mathrm {in} }}{\frac {1}{j\omega C}}}\\V_{\mathrm {in} }&\approx {\frac {I}{j\omega C}}=V_{C}\,.\end{aligned}}$

Now,

${\begin{aligned}V_{R}&=IR=C{\frac {dV_{C}}{dt}}R\\V_{R}&\approx RC{\frac {dV_{in}}{dt}}\,,\end{aligned}}$

which is adifferentiatoracross the resistor.

Integrationanddifferentiationcan also be achieved by placing resistors and capacitors as appropriate on the input andfeedbackloop ofoperational amplifiers(seeoperational amplifier integratorandoperational amplifier differentiator).

PWM RC Series Circuit

Parallel circuit

ParallelRC circuit

The parallel RC circuit is generally of less interest than the series circuit. This is largely because the output voltageV_outis equal to the input voltageV_in— as a result, this circuit does not act as a filter on the input signal unless fed by acurrent source.

With complex impedances:

${\begin{aligned}I_{R}&={\frac {V_{\mathrm {in} }}{R}}\\I_{C}&=j\omega CV_{\mathrm {in} }\,.\end{aligned}}$

This shows that the capacitor current is 90° out of phase with the resistor (and source) current. Alternatively, the governing differential equations may be used:

${\begin{aligned}I_{R}&={\frac {V_{\mathrm {in} }}{R}}\\I_{C}&=C{\frac {dV_{\mathrm {in} }}{dt}}\,.\end{aligned}}$

When fed by a current source, the transfer function of a parallel RC circuit is:

${\frac {V_{\mathrm {out} }}{I_{\mathrm {in} }}}={\frac {R}{1+sRC}}\,.$

Synthesis

It is sometimes required tosynthesisean RC circuit from a givenrational functionins.For synthesis to be possible in passive elements, the function must be apositive-real function.To synthesise as an RC circuit, all the critical frequencies (poles and zeroes) must be on the negative real axis and alternate between poles and zeroes with an equal number of each. Further, the critical frequency nearest the origin must be a pole, assuming the rational function represents an impedance rather than an admittance.

The synthesis can be achieved with a modification of theFoster synthesisorCauer synthesisused to synthesiseLC circuits.In the case of Cauer synthesis, aladder networkof resistors and capacitors will result.

See also

• RC time constant
• RL circuit
• LC circuit
• RLC circuit
• Electrical network
• List of electronics topics
• Step response

Bibliography

• Bakshi, U.A.; Bakshi, A.V.,Circuit Analysis - II,Technical Publications, 2009ISBN9788184315974.
• Horowitz, Paul; Hill, Winfield,The Art of Electronics(3rd edition), Cambridge University Press, 2015ISBN0521809266.