Radius of convergence
Inmathematics,theradius of convergenceof apower seriesis the radius of the largestdiskat thecenter of the seriesin which the seriesconverges.It is either a non-negative real number or.When it is positive, the power seriesconverges absolutelyanduniformly on compact setsinside the open disk of radius equal to the radius of convergence, and it is theTaylor seriesof theanalytic functionto which it converges. In case of multiple singularities of a function (singularities are those values of the argument for which the function is not defined), the radius of convergence is the shortest or minimum of all the respective distances (which are all non-negative numbers) calculated from the center of the disk of convergence to the respective singularities of the function.
Definition
[edit]For a power seriesfdefined as:
where
- ais acomplexconstant, the center of thediskof convergence,
- cnis then-th complex coefficient, and
- zis a complex variable.
The radius of convergenceris a nonnegative real number orsuch that the series converges if
and diverges if
Some may prefer an alternative definition, as existence is obvious:
On the boundary, that is, where |z−a| =r,the behavior of the power series may be complicated, and the series may converge for some values ofzand diverge for others. The radius of convergence is infinite if the series converges for allcomplex numbersz.[1]
Finding the radius of convergence
[edit]Two cases arise:
- The first case is theoretical: when you know all the coefficientsthen you take certain limits and find the precise radius of convergence.
- The second case is practical: when you construct a power series solution of a difficult problem you typically will only know a finite number of terms in a power series, anywhere from a couple of terms to a hundred terms. In this second case, extrapolating a plot estimates the radius of convergence.
Theoretical radius
[edit]The radius of convergence can be found by applying theroot testto the terms of the series. The root test uses the number
"lim sup" denotes thelimit superior.The root test states that the series converges ifC< 1 and diverges ifC> 1. It follows that the power series converges if the distance fromzto the centerais less than
and diverges if the distance exceeds that number; this statement is theCauchy–Hadamard theorem.Note thatr= 1/0 is interpreted as an infinite radius, meaning thatfis anentire function.
The limit involved in theratio testis usually easier to compute, and when that limit exists, it shows that the radius of convergence is finite.
This is shown as follows. The ratio test says the series converges if
That is equivalent to
Practical estimation of radius in the case of real coefficients
[edit]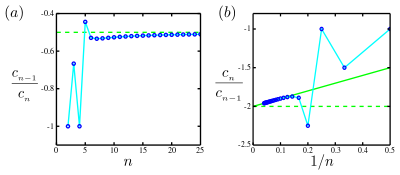
The solid green line is thestraight-lineasymptotein the Domb–Sykes plot,[2]plot (b), which intercepts the vertical axis at −2 and has a slope +1. Thus there is a singularity atand so the radius of convergence is
Usually, in scientific applications, only a finite number of coefficientsare known. Typically, asincreases, these coefficients settle into a regular behavior determined by the nearest radius-limiting singularity. In this case, two main techniques have been developed, based on the fact that the coefficients of a Taylor series are roughly exponential with ratiowhereris the radius of convergence.
- The basic case is when the coefficients ultimately share a common sign or alternate in sign. As pointed out earlier in the article, in many cases the limitexists, and in this case.Negativemeans the convergence-limiting singularity is on the negative axis. Estimate this limit, by plotting theversus,and graphically extrapolate to(effectively) via alinear fit.The intercept withestimates the reciprocal of the radius of convergence,.This plot is called aDomb–Sykes plot.[3]
- The more complicated case is when the signs of the coefficients have a more complex pattern. Mercer and Roberts proposed the following procedure.[4]Define the associated sequencePlot the finitely many knownversus,and graphically extrapolate tovia a linear fit. The intercept withestimates the reciprocal of the radius of convergence,.This procedure also estimates two other characteristics of the convergence limiting singularity. Suppose the nearest singularity is of degreeand has angleto the real axis. Then the slope of the linear fit given above is.Further, plotversus,then a linear fit extrapolated tohas intercept at.
Radius of convergence in complex analysis
[edit]A power series with a positive radius of convergence can be made into aholomorphic functionby taking its argument to be a complex variable. The radius of convergence can be characterized by the following theorem:
- The radius of convergence of a power seriesfcentered on a pointais equal to the distance fromato the nearest point wherefcannot be defined in a way that makes it holomorphic.
The set of all points whose distance toais strictly less than the radius of convergence is called thedisk of convergence.

The nearest pointmeans the nearest point in thecomplex plane,not necessarily on the real line, even if the center and all coefficients are real. For example, the function
has no singularities on the real line, sincehas no real roots. Its Taylor series about 0 is given by
The root test shows that its radius of convergence is 1. In accordance with this, the functionf(z) has singularities at ±i,which are at a distance 1 from 0.
For a proof of this theorem, seeanalyticity of holomorphic functions.
A simple example
[edit]The arctangent function oftrigonometrycan be expanded in a power series:
It is easy to apply the root test in this case to find that the radius of convergence is 1.
A more complicated example
[edit]Consider this power series:
where the rational numbersBnare theBernoulli numbers.It may be cumbersome to try to apply the ratio test to find the radius of convergence of this series. But the theorem of complex analysis stated above quickly solves the problem. Atz= 0, there is in effect no singularity sincethe singularity is removable.The only non-removable singularities are therefore located at theotherpoints where the denominator is zero. We solve
by recalling that ifz=x+iyandeiy= cos(y) +isin(y)then
and then takexandyto be real. Sinceyis real, the absolute value ofcos(y) +isin(y)is necessarily 1. Therefore, the absolute value ofezcan be 1 only ifexis 1; sincexis real, that happens only ifx= 0. Thereforezis purely imaginary andcos(y) +isin(y) = 1.Sinceyis real, that happens only if cos(y) = 1 and sin(y) = 0, so thatyis an integer multiple of 2π.Consequently the singular points of this function occur at
- z= a nonzero integer multiple of 2πi.
The singularities nearest 0, which is the center of the power series expansion, are at ±2πi.The distance from the center to either of those points is 2π,so the radius of convergence is 2π.
Convergence on the boundary
[edit]If the power series is expanded around the pointaand the radius of convergence isr,then the set of all pointszsuch that|z−a| =ris acirclecalled theboundaryof the disk of convergence. A power series may diverge at every point on the boundary, or diverge on some points and converge at other points, or converge at all the points on the boundary. Furthermore, even if the series converges everywhere on the boundary (even uniformly), it does not necessarily converge absolutely.
Example 1: The power series for the functionf(z) = 1/(1 −z),expanded aroundz= 0,which is simply
has radius of convergence 1 and diverges at every point on the boundary.
Example 2: The power series forg(z) = −ln(1 −z),expanded aroundz= 0,which is
has radius of convergence 1, and diverges forz= 1but converges for all other points on the boundary. The functionf(z)of Example 1 is thederivativeofg(z).
Example 3: The power series
has radius of convergence 1 and converges everywhere on the boundary absolutely. Ifhis the function represented by this series on the unit disk, then the derivative ofh(z) is equal tog(z)/zwithgof Example 2. It turns out thath(z)is thedilogarithmfunction.
Example 4: The power series
has radius of convergence 1 and convergesuniformlyon the entire boundary|z| = 1,but does notconverge absolutelyon the boundary.[5]
Rate of convergence
[edit]If we expand the function
around the pointx= 0, we find out that the radius of convergence of this series ismeaning that this series converges for all complex numbers. However, in applications, one is often interested in the precision of anumerical answer.Both the number of terms and the value at which the series is to be evaluated affect the accuracy of the answer. For example, if we want to calculatesin(0.1)accurate up to five decimal places, we only need the first two terms of the series. However, if we want the same precision forx= 1we must evaluate and sum the first five terms of the series. Forsin(10),one requires the first 18 terms of the series, and forsin(100)we need to evaluate the first 141 terms.
So for these particular values the fastest convergence of a power series expansion is at the center, and as one moves away from the center of convergence, therate of convergenceslows down until you reach the boundary (if it exists) and cross over, in which case theserieswill diverge.
Abscissa of convergence of a Dirichlet series
[edit]An analogous concept is theabscissa of convergence of a Dirichlet series
Such a series converges if the real part ofsis greater than a particular number depending on the coefficientsan:theabscissaof convergence.
Notes
[edit]- ^Mathematical Analysis-II.Krishna Prakashan Media. 16 November 2010.
- ^See Figure 8.1 in:Hinch, E.J. (1991),Perturbation Methods,Cambridge Texts in Applied Mathematics, vol. 6, Cambridge University Press, p. 146,ISBN0-521-37897-4
- ^Domb, C.; Sykes, M.F. (1957), "On the susceptibility of a ferromagnetic above the Curie point",Proc. R. Soc. Lond. A,240(1221): 214–228,Bibcode:1957RSPSA.240..214D,doi:10.1098/rspa.1957.0078,S2CID119974403
- ^Mercer, G.N.; Roberts, A.J. (1990), "A centre manifold description of contaminant dispersion in channels with varying flow properties",SIAM J. Appl. Math.,50(6): 1547–1565,doi:10.1137/0150091
- ^Sierpiński, W.(1918)."O szeregu potęgowym, który jest zbieżny na całem swem kole zbieżności jednostajnie, ale nie bezwzględnie".Prace Matematyczno-Fizyczne.29(1): 263–266.
References
[edit]- Brown, James; Churchill, Ruel (1989),Complex variables and applications,New York:McGraw-Hill,ISBN978-0-07-010905-6
- Stein, Elias;Shakarchi, Rami (2003),Complex Analysis,Princeton, New Jersey:Princeton University Press,ISBN0-691-11385-8







![{\displaystyle C=\limsup _{n\to \infty }{\sqrt[{n}]{|c_{n}(z-a)^{n}|}}=\limsup _{n\to \infty }\left({\sqrt[{n}]{|c_{n}|}}\right)|z-a|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c67486298c59df5fc7583a5cc253024ebc9045ea)
![{\displaystyle r={\frac {1}{\limsup _{n\to \infty }{\sqrt[{n}]{|c_{n}|}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb0428211dc308307cbbd69ed6151785382c549b)





































