Rectified 5-simplexes
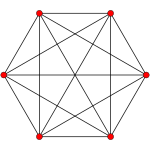 5-simplex |
 Rectified 5-simplex |
 Birectified 5-simplex |
| Orthogonal projectionsin A5Coxeter plane | ||
|---|---|---|
In five-dimensionalgeometry,arectified 5-simplexis a convexuniform 5-polytope,being arectificationof the regular5-simplex.
There are three unique degrees of rectifications, including the zeroth, the 5-simplex itself. Vertices of therectified 5-simplexare located at the edge-centers of the5-simplex.Vertices of thebirectified 5-simplexare located in the triangular face centers of the5-simplex.
Rectified 5-simplex
[edit]| Rectified 5-simplex Rectified hexateron (rix) | ||
|---|---|---|
| Type | uniform 5-polytope | |
| Schläfli symbol | r{34} or | |
| Coxeter diagram | or | |
| 4-faces | 12 | 6{3,3,3} 6r{3,3,3} |
| Cells | 45 | 15{3,3} 30r{3,3} |
| Faces | 80 | 80{3} |
| Edges | 60 | |
| Vertices | 15 | |
| Vertex figure |  {}×{3,3} | |
| Coxeter group | A5,[34], order 720 | |
| Dual | ||
| Base point | (0,0,0,0,1,1) | |
| Circumradius | 0.645497 | |
| Properties | convex,isogonalisotoxal | |
Infive-dimensionalgeometry,arectified 5-simplexis auniform 5-polytopewith 15vertices,60edges,80triangularfaces,45cells(30tetrahedral,and 15octahedral), and 124-faces(65-celland 6rectified 5-cells). It is also called03,1for its branching Coxeter-Dynkin diagram, shown as![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
E. L. Elteidentified it in 1912 as a semiregular polytope, labeling it as S1
5.
Alternate names
[edit]- Rectified hexateron (Acronym: rix) (Jonathan Bowers)
Coordinates
[edit]The vertices of the rectified 5-simplex can be more simply positioned on ahyperplanein 6-space as permutations of (0,0,0,0,1,1)or(0,0,1,1,1,1). These construction can be seen as facets of therectified 6-orthoplexorbirectified 6-cuberespectively.
As a configuration
[edit]Thisconfiguration matrixrepresents the rectified 5-simplex. The rows and columns correspond to vertices, edges, faces, cells and 4-faces. The diagonal numbers say how many of each element occur in the whole rectified 5-simplex. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[1][2]
The diagonal f-vector numbers are derived through theWythoff construction,dividing the full group order of a subgroup order by removing one mirror at a time.[3]
| A5 | k-face | fk | f0 | f1 | f2 | f3 | f4 | k-figure | notes | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A3A1 | ( ) | f0 | 15 | 8 | 4 | 12 | 6 | 8 | 4 | 2 | {3,3}×{ } | A5/A3A1= 6!/4!/2 = 15 | |
| A2A1 | { } | f1 | 2 | 60 | 1 | 3 | 3 | 3 | 3 | 1 | {3}∨( ) | A5/A2A1= 6!/3!/2 = 60 | |
| A2A2 | r{3} | f2 | 3 | 3 | 20 | * | 3 | 0 | 3 | 0 | {3} | A5/A2A2= 6!/3!/3! =20 | |
| A2A1 | {3} | 3 | 3 | * | 60 | 1 | 2 | 2 | 1 | { }×( ) | A5/A2A1= 6!/3!/2 = 60 | ||
| A3A1 | r{3,3} | f3 | 6 | 12 | 4 | 4 | 15 | * | 2 | 0 | { } | A5/A3A1= 6!/4!/2 = 15 | |
| A3 | {3,3} | 4 | 6 | 0 | 4 | * | 30 | 1 | 1 | A5/A3= 6!/4! = 30 | |||
| A4 | r{3,3,3} | f4 | 10 | 30 | 10 | 20 | 5 | 5 | 6 | * | ( ) | A5/A4= 6!/5! = 6 | |
| A4 | {3,3,3} | 5 | 10 | 0 | 10 | 0 | 5 | * | 6 | A5/A4= 6!/5! = 6 | |||
Images
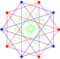
[edit] Stereographic projectionof spherical form |
| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | [6] | [5] |
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|

|
| Dihedral symmetry | [4] | [3] |
Related polytopes
[edit]The rectified 5-simplex, 031,is second in a dimensional series of uniform polytopes, expressed byCoxeteras 13kseries. The fifth figure is a Euclidean honeycomb,331,and the final is a noncompact hyperbolic honeycomb, 431.Each progressiveuniform polytopeis constructed from the previous as itsvertex figure.
| n | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| Coxeter group |
A3A1 | A5 | D6 | E7 | = E7+ | =E7++ |
| Coxeter diagram |
||||||
| Symmetry | [3−1,3,1] | [30,3,1] | [31,3,1] | [32,3,1] | [33,3,1] | [34,3,1] |
| Order | 48 | 720 | 23,040 | 2,903,040 | ∞ | |
| Graph | 
|
|

|

|
- | - |
| Name | −131 | 031 | 131 | 231 | 331 | 431 |
Birectified 5-simplex
[edit]| Birectified 5-simplex Birectified hexateron (dot) | ||
|---|---|---|
| Type | uniform 5-polytope | |
| Schläfli symbol | 2r{34} = {32,2} or | |
| Coxeter diagram | or | |
| 4-faces | 12 | 12r{3,3,3} |
| Cells | 60 | 30{3,3} 30r{3,3} |
| Faces | 120 | 120{3} |
| Edges | 90 | |
| Vertices | 20 | |
| Vertex figure |  {3}×{3} | |
| Coxeter group | A5×2, [[34]], order 1440 | |
| Dual | ||
| Base point | (0,0,0,1,1,1) | |
| Circumradius | 0.866025 | |
| Properties | convex,isogonalisotoxal | |
Thebirectified 5-simplexisisotopic,with all 12 of its facets asrectified 5-cells.It has 20vertices,90edges,120triangularfaces,60cells(30tetrahedral,and 30octahedral).
E. L. Elteidentified it in 1912 as a semiregular polytope, labeling it as S2
5.
It is also called02,2for its branching Coxeter-Dynkin diagram, shown as![]()
![]()
![]()
![]()
![]() .It is seen in thevertex figureof the 6-dimensional122,
.It is seen in thevertex figureof the 6-dimensional122,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Alternate names
[edit]- Birectified hexateron
- dodecateron (Acronym: dot) (For 12-facetted polyteron) (Jonathan Bowers)
Construction
[edit]The elements of the regular polytopes can be expressed in aconfiguration matrix.Rows and columns reference vertices, edges, faces, and cells, with diagonal element their counts (f-vectors). The nondiagonal elements represent the number of row elements are incident to the column element.[4][5]
The diagonal f-vector numbers are derived through theWythoff construction,dividing the full group order of a subgroup order by removing one mirror at a time.[6]
| A5 | k-face | fk | f0 | f1 | f2 | f3 | f4 | k-figure | notes | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A2A2 | ( ) | f0 | 20 | 9 | 9 | 9 | 3 | 9 | 3 | 3 | 3 | {3}×{3} | A5/A2A2= 6!/3!/3! = 20 | |
| A1A1A1 | { } | f1 | 2 | 90 | 2 | 2 | 1 | 4 | 1 | 2 | 2 | { }∨{ } | A5/A1A1A1= 6!/2/2/2 = 90 | |
| A2A1 | {3} | f2 | 3 | 3 | 60 | * | 1 | 2 | 0 | 2 | 1 | { }∨( ) | A5/A2A1= 6!/3!/2 = 60 | |
| A2A1 | 3 | 3 | * | 60 | 0 | 2 | 1 | 1 | 2 | |||||
| A3A1 | {3,3} | f3 | 4 | 6 | 4 | 0 | 15 | * | * | 2 | 0 | { } | A5/A3A1= 6!/4!/2 = 15 | |
| A3 | r{3,3} | 6 | 12 | 4 | 4 | * | 30 | * | 1 | 1 | A5/A3= 6!/4! = 30 | |||
| A3A1 | {3,3} | 4 | 6 | 0 | 4 | * | * | 15 | 0 | 2 | A5/A3A1= 6!/4!/2 = 15 | |||
| A4 | r{3,3,3} | f4 | 10 | 30 | 20 | 10 | 5 | 5 | 0 | 6 | * | ( ) | A5/A4= 6!/5! = 6 | |
| A4 | 10 | 30 | 10 | 20 | 0 | 5 | 5 | * | 6 | |||||
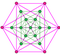
Images
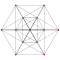
[edit]The A5 projection has an identical appearance toMetatron's Cube.[7]
| Ak Coxeter plane |
A5 | A4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | [6] | [[5]]=[10] |
| Ak Coxeter plane |
A3 | A2 |
| Graph | 
|

|
| Dihedral symmetry | [4] | [[3]]=[6] |
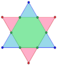
Intersection of two 5-simplices
[edit]
|
Thebirectified 5-simplexis theintersectionof two regular5-simplexesindualconfiguration. The vertices of abirectificationexist at the center of the faces of the original polytope(s). This intersection is analogous to the 3Dstellated octahedron,seen as a compound of two regulartetrahedraand intersected in a centraloctahedron,while that is a firstrectificationwhere vertices are at the center of the original edges.

|
| Dual 5-simplexes (red and blue), and their birectified 5-simplex intersection in green, viewed in A5 and A4 Coxeter planes. The simplexes overlap in the A5 projection and are drawn in magenta. |
It is also the intersection of a6-cubewith the hyperplane that bisects the 6-cube's long diagonal orthogonally. In this sense it is the 5-dimensional analog of the regular hexagon,octahedron,andbitruncated 5-cell.This characterization yields simple coordinates for the vertices of a birectified 5-simplex in 6-space: the 20 distinct permutations of (1,1,1,−1,−1,−1).
The vertices of thebirectified 5-simplexcan also be positioned on ahyperplanein 6-space as permutations of (0,0,0,1,1,1). This construction can be seen as facets of thebirectified 6-orthoplex.
Related polytopes
[edit]k_22 polytopes
[edit]Thebirectified 5-simplex,022,is second in a dimensional series of uniform polytopes, expressed byCoxeteras k22series. Thebirectified 5-simplexis the vertex figure for the third, the122.The fourth figure is a Euclidean honeycomb,222,and the final is a noncompact hyperbolic honeycomb, 322.Each progressiveuniform polytopeis constructed from the previous as itsvertex figure.
| Space | Finite | Euclidean | Hyperbolic | ||
|---|---|---|---|---|---|
| n | 4 | 5 | 6 | 7 | 8 |
| Coxeter group |
A2A2 | E6 | =E6+ | =E6++ | |
| Coxeter diagram |
|||||
| Symmetry | [[32,2,-1]] | [[32,2,0]] | [[32,2,1]] | [[32,2,2]] | [[32,2,3]] |
| Order | 72 | 1440 | 103,680 | ∞ | |
| Graph | 
|
|

|
∞ | ∞ |
| Name | −122 | 022 | 122 | 222 | 322 |
Isotopics polytopes
[edit]| Dim. | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| Name Coxeter |
Hexagon t{3} = {6} |
Octahedron r{3,3} = {31,1} = {3,4} |
Decachoron 2t{33} |
Dodecateron 2r{34}= {32,2} |
Tetradecapeton 3t{35} |
Hexadecaexon 3r{36}= {33,3} |
Octadecazetton 4t{37} |
| Images | 
|
 
|
 
|
|
|
 
|
 
|
| Vertex figure | ( )∨( ) |  { }×{ } |
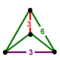 { }∨{ } |
 {3}×{3} |
 {3}∨{3} |
{3,3}×{3,3} | 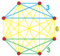 {3,3}∨{3,3} |
| Facets | {3} |
t{3,3} |
r{3,3,3} |
2t{3,3,3,3} |
2r{3,3,3,3,3} |
3t{3,3,3,3,3,3} | |
| As intersecting dual simplexes |
 |
 |
 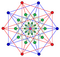 |
Related uniform 5-polytopes
[edit]This polytope is thevertex figureof the6-demicube,and theedge figureof the uniform231polytope.
It is also one of 19uniform polyterabased on the [3,3,3,3]Coxeter group,all shown here in A5Coxeter planeorthographic projections.(Vertices are colored by projection overlap order, red, orange, yellow, green, cyan, blue, purple having progressively more vertices)
| A5 polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 t0 |
 t1 |
 t2 |
 t0,1 |
 t0,2 |
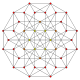 t1,2 |
 t0,3 | |||||
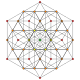 t1,3 |
 t0,4 |
 t0,1,2 |
 t0,1,3 |
 t0,2,3 |
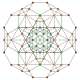 t1,2,3 |
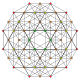 t0,1,4 | |||||
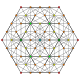 t0,2,4 |
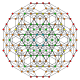 t0,1,2,3 |
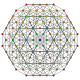 t0,1,2,4 |
 t0,1,3,4 |
 t0,1,2,3,4 | |||||||
References
[edit]- ^Coxeter, Regular Polytopes, sec 1.8 Configurations
- ^Coxeter, Complex Regular Polytopes, p.117
- ^Klitzing, Richard."o3x3o3o3o - rix".
- ^Coxeter, Regular Polytopes, sec 1.8 Configurations
- ^Coxeter, Complex Regular Polytopes, p.117
- ^Klitzing, Richard."o3o3x3o3o - dot".
- ^Melchizedek, Drunvalo (1999).The Ancient Secret of the Flower of Life.Vol. 1. Light Technology Publishing.p.160 Figure 6-12
- H.S.M. Coxeter:
- H.S.M. Coxeter,Regular Polytopes,3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter,edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,ISBN978-0-471-01003-6[1]
- (Paper 22) H.S.M. Coxeter,Regular and Semi Regular Polytopes I,[Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter,Regular and Semi-Regular Polytopes II,[Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter,Regular and Semi-Regular Polytopes III,[Math. Zeit. 200 (1988) 3-45]
- Norman JohnsonUniform Polytopes,Manuscript (1991)
- N.W. Johnson:The Theory of Uniform Polytopes and Honeycombs,Ph.D.
- Klitzing, Richard."5D uniform polytopes (polytera)".o3x3o3o3o - rix, o3o3x3o3o - dot
External links
[edit]- Glossary for hyperspace,George Olshevsky.
- Polytopes of Various Dimensions,Jonathan Bowers
- Rectified uniform polytera(Rix), Jonathan Bowers
- Multi-dimensional Glossary








