Trapezoid

Trapezoid (AmE) Trapezium (BrE)
Trapezoid or trapezium
Type	quadrilateral
Edgesandvertices	4
Area	${\tfrac {a+b}{2}}h$
Properties	convex

Ingeometry,atrapezoid(/ˈtræpəzɔɪd/) inNorth American English,ortrapezium(/trəˈpiːziəm/) inBritish English,is aquadrilateralthat has one pair ofparallelsides.

The parallel sides are called thebasesof the trapezoid. The other two sides are called thelegs(or thelateral sides) if they are not parallel; otherwise, the trapezoid is a parallelogram, and there are two pairs of bases. Ascalene trapezoidis a trapezoid with no sides ofequalmeasure,in contrast with thespecial casesbelow.

A trapezoid is usually considered to be aconvexquadrilateral inEuclidean geometry,but there are alsocrossedcases. IfABCDis a convex trapezoid, thenABDCis a crossed trapezoid. The metric formulas in this article apply in convex trapezoids.

Etymology andtrapeziumversustrapezoid

Hutton's definitions in 1795

The ancient Greek mathematicianEucliddefined five types of quadrilateral, of which four had two sets of parallel sides (known in English as square, rectangle, rhombus and rhomboid) and the last did not have two sets of parallel sides – a τραπέζια (trapezialiterally 'table', itself from τετράς (tetrás) 'four' + πέζα (péza) 'foot; end, border, edge').

Two types oftrapeziawere introduced byProclus(AD 412 to 485) in his commentary on the first book ofEuclid's Elements:

• one pair of parallel sides – atrapezium(τραπέζιον), divided into isosceles (equal legs) and scalene (unequal) trapezia
• no parallel sides –trapezoid(τραπεζοειδή,trapezoeidé,literally 'trapezium-like' (εἶδοςmeans 'resembles'), in the same way ascuboidmeans 'cube-like' andrhomboidmeans 'rhombus-like')

All European languages follow Proclus's structureas did English until the late 18th century, until an influential mathematical dictionary published byCharles Huttonin 1795 supported without explanation a transposition of the terms. This was reversed in British English in about 1875, but it has been retained in American English to the present.

The following table compares usages, with the most specific definitions at the top to the most general at the bottom.

Type	Sets of parallel sides	Image	Original terminology			Modern terminology
			Euclid(Definition 22)	Proclus(Definitions 30-34, quoting Posidonius)	Euclid / Proclus definition	British English	American English
Parallelogram	2		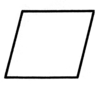ῥόμβος (rhombos)		equilateral but not right-angled	Rhombus/Parallelogram
			ῥομβοειδὲς (rhomboides)		opposite sides and angles equal to one another but not equilateral nor right-angled	Rhomboid/Parallelogram
Non-parallelogram	1		τραπέζια (trapezia)	τραπέζιον ἰσοσκελὲς (trapezionisoskelés)	Two parallel sides, and a line of symmetry	Isosceles Trapezium	Isosceles Trapezoid
				τραπέζιον σκαληνὸν (trapezionskalinón)	Two parallel sides, and no line of symmetry	Trapezium	Trapezoid
	0			τραπέζοειδὲς (trapezoides)	No parallel sides	Irregular quadrilateral/Trapezoid	Trapezium

Inclusive versus exclusive definition

There is some disagreement whetherparallelograms,which have two pairs of parallel sides, should be regarded as trapezoids.

Some define a trapezoid as a quadrilateral havingonlyone pair of parallel sides (the exclusive definition), thereby excluding parallelograms.Some sources use the termproper trapezoidto describe trapezoids under the exclusive definition, analogous to uses of the wordproperin some other mathematical objects.

Othersdefine a trapezoid as a quadrilateral withat leastone pair of parallel sides (the inclusive definition), making the parallelogram a special type of trapezoid. The latter definition is consistent with its uses in higher mathematics such ascalculus.This article uses the inclusive definition and considers parallelograms as special cases of a trapezoid. This is also advocated in thetaxonomy of quadrilaterals.

Under the inclusive definition, all parallelograms (includingrhombuses,squaresand non-squarerectangles) are trapezoids. Rectangles have mirror symmetry on mid-edges; rhombuses have mirror symmetry on vertices, while squares have mirror symmetry on both mid-edges and vertices.

Special cases

Trapezoid special cases. The orange figures also qualify as parallelograms.

Aright trapezoid(also calledright-angled trapezoid) has two adjacentright angles.Right trapezoids are used in thetrapezoidal rulefor estimating areas under a curve.

Anacute trapezoidhas two adjacent acute angles on its longerbaseedge.

Anobtuse trapezoidon the other hand has one acute and one obtuse angle on eachbase.

Anisosceles trapezoidis a trapezoid where the base angles have the same measure. As a consequence the two legs are also of equal length and it hasreflection symmetry.This is possible for acute trapezoids or right trapezoids (as rectangles).

Aparallelogramis (under the inclusive definition) a trapezoid with two pairs of parallel sides. A parallelogram has central 2-foldrotational symmetry(orpoint reflectionsymmetry). It is possible for obtuse trapezoids or right trapezoids (rectangles).

Atangential trapezoidis a trapezoid that has anincircle.

ASaccheri quadrilateralis similar to a trapezoid in thehyperbolicplane, with two adjacent right angles, while it is a rectangle in theEuclidean plane.ALambert quadrilateralin the hyperbolic plane has 3 right angles.

Condition of existence

Four lengthsa,c,b,dcan constitute the consecutive sides of a non-parallelogram trapezoid withaandbparallel only when

$\displaystyle |d-c|<|b-a|<d+c.$

The quadrilateral is a parallelogram when$d-c=b-a=0$,but it is anex-tangential quadrilateral(which is not a trapezoid) when$|d-c|=|b-a|\neq 0$.

Characterizations

general trapezoid/trapezium:
parallel sides:$a,\,b$with$a<b$
legs:$c,\,d$
diagonals:$q,\,p$
midsegment:$m$
height/altitude:$h$

trapezoid/trapezium with opposing triangles$S,\,T$formed by the diagonals

Given a convex quadrilateral, the following properties are equivalent, and each implies that the quadrilateral is a trapezoid:

• It has two adjacentanglesthat aresupplementary,that is, they add up to 180degrees.
• The angle between a side and adiagonalis equal to the angle between the opposite side and the same diagonal.
• The diagonals cut each other in mutually the sameratio(this ratio is the same as that between the lengths of the parallel sides).
• The diagonals cut the quadrilateral into fourtrianglesof which one opposite pair have equal areas.
• The product of the areas of the two triangles formed by one diagonal equals the product of the areas of the two triangles formed by the other diagonal.
• The areasSandTof some two opposite triangles of the four triangles formed by the diagonals satisfy the equation

${\sqrt {K}}={\sqrt {S}}+{\sqrt {T}},$

whereKis the area of the quadrilateral.

• The midpoints of two opposite sides of the trapezoid and the intersection of the diagonals arecollinear.
• The angles in the quadrilateralABCDsatisfy$\sin A\sin C=\sin B\sin D.$
• The cosines of two adjacent anglessumto 0, as do the cosines of the other two angles.
• The cotangents of two adjacent angles sum to 0, as do the cotangents of the other two adjacent angles.
• One bimedian divides the quadrilateral into two quadrilaterals of equal areas.
• Twice the length of the bimedian connecting the midpoints of two opposite sides equals the sum of the lengths of the other sides.

Additionally, the following properties are equivalent, and each implies that opposite sidesaandbare parallel:

• The consecutive sidesa,c,b,dand the diagonalsp,qsatisfy the equation

$p^{2}+q^{2}=c^{2}+d^{2}+2ab.$

• The distancevbetween the midpoints of the diagonals satisfies the equation

$v={\frac {|a-b|}{2}}.$

Midsegment and height

Themidsegment(also called the median or midline) of a trapezoid is the segment that joins themidpointsof the legs. It is parallel to the bases. Its lengthmis equal to the average of the lengths of the basesaandbof the trapezoid,

$m={\frac {a+b}{2}}.$

The midsegment of a trapezoid is one of the twobimedians(the other bimedian divides the trapezoid into equal areas).

Theheight(or altitude) is theperpendiculardistance between the bases. In the case that the two bases have different lengths (a≠b), the height of a trapezoidhcan be determined by the length of its four sides using the formula

$h={\frac {\sqrt {(p-a)(p-b)(p-b-d)(p-b-c)}}{2|b-a|}}$

wherecanddare the lengths of the legs and$p=a+b+c+d$.

Area

The areaKof a trapezoid is given by

$K={\frac {a+b}{2}}\cdot h=mh$

whereaandbare the lengths of the parallel sides,his the height (the perpendicular distance between these sides), andmis thearithmetic meanof the lengths of the two parallel sides. In 499 ADAryabhata,a greatmathematician-astronomerfrom the classical age ofIndian mathematicsandIndian astronomy,used this method in theAryabhatiya(section 2.8). This yields as aspecial casethe well-known formula for the area of atriangle,by considering a triangle as a degenerate trapezoid in which one of the parallel sides has shrunk to a point.

The 7th-century Indian mathematicianBhāskara Iderived the following formula for the area of a trapezoid with consecutive sidesa,c,b,d:

$K={\frac {1}{2}}(a+b){\sqrt {c^{2}-{\frac {1}{4}}\left((b-a)+{\frac {c^{2}-d^{2}}{b-a}}\right)^{2}}}$

whereaandbare parallel andb>a.This formula can be factored into a more symmetric version

$K={\frac {a+b}{4|b-a|}}{\sqrt {(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}.$

When one of the parallel sides has shrunk to a point (saya= 0), this formula reduces toHeron's formulafor the area of a triangle.

Another equivalent formula for the area, which more closely resembles Heron's formula, is

$K={\frac {a+b}{|b-a|}}{\sqrt {(s-b)(s-a)(s-b-c)(s-b-d)}}$

where$s={\tfrac {1}{2}}(a+b+c+d)$is thesemiperimeterof the trapezoid. (This formula is similar toBrahmagupta's formula,but it differs from it, in that a trapezoid might not becyclic(inscribed in a circle). The formula is also a special case ofBretschneider's formulafor a generalquadrilateral).

From Bretschneider's formula, it follows that

$K={\sqrt {{\frac {(ab^{2}-a^{2}b-ad^{2}+bc^{2})(ab^{2}-a^{2}b-ac^{2}+bd^{2})}{4(b-a)^{2}}}-\left({\frac {c^{2}+d^{2}-a^{2}-b^{2}}{4}}\right)^{2}}}.$

The line that joins the midpoints of the parallel sides, bisects the area.

Diagonals

The lengths of the diagonals are

$p={\sqrt {\frac {ab^{2}-a^{2}b-ac^{2}+bd^{2}}{b-a}}},$

$q={\sqrt {\frac {ab^{2}-a^{2}b-ad^{2}+bc^{2}}{b-a}}}$

whereais the short base,bis the long base, andcanddare the trapezoid legs.

If the trapezoid is divided into four triangles by its diagonalsACandBD(as shown on the right), intersecting atO,then the area of$\triangle$AODis equal to that of$\triangle$BOC,and the product of the areas of$\triangle$AODand$\triangle$BOCis equal to that of$\triangle$AOBand$\triangle$COD.The ratio of the areas of each pair of adjacent triangles is the same as that between the lengths of the parallel sides.

Let the trapezoid have verticesA,B,C,andDin sequence and have parallel sidesABandDC.LetEbe the intersection of the diagonals, and letFbe on sideDAandGbe on sideBCsuch thatFEGis parallel toABandCD.ThenFGis theharmonic meanofABandDC:

${\frac {1}{FG}}={\frac {1}{2}}\left({\frac {1}{AB}}+{\frac {1}{DC}}\right).$

The line that goes through both the intersection point of the extended nonparallel sides and the intersection point of the diagonals, bisects each base.

Other properties

The center of area (center of mass for a uniformlamina) lies along the line segment joining the midpoints of the parallel sides, at a perpendicular distancexfrom the longer sidebgiven by

$x={\frac {h}{3}}\left({\frac {2a+b}{a+b}}\right).$

The center of area divides this segment in the ratio (when taken from the short to the long side)

${\frac {a+2b}{2a+b}}.$

If the angle bisectors to anglesAandBintersect atP,and the angle bisectors to anglesCandDintersect atQ,then

$PQ={\frac {|AD+BC-AB-CD|}{2}}.$

Applications

TheTemple of Dendurin theMetropolitan Museum of ArtinNew York City

Architecture

In architecture the word is used to refer to symmetrical doors, windows, and buildings built wider at the base, tapering toward the top, in Egyptian style. If these have straight sides and sharp angular corners, their shapes are usuallyisosceles trapezoids.This was the standard style for the doors and windows of theInca.

Geometry

Thecrossed ladders problemis the problem of finding the distance between the parallel sides of a right trapezoid, given the diagonal lengths and the distance from the perpendicular leg to the diagonal intersection.

Biology

Example of a trapeziformpronotumoutlined on aspurge bug

Inmorphology,taxonomyand other descriptive disciplines in which a term for such shapes is necessary, terms such astrapezoidalortrapeziformcommonly are useful in descriptions of particular organs or forms.

Computer engineering

In computer engineering, specifically digital logic and computer architecture, trapezoids are typically utilized to symbolizemultiplexors.Multiplexors are logic elements that select between multiple elements and produce a single output based on a select signal. Typical designs will employ trapezoids without specifically stating they are multiplexors as they are universally equivalent.

See also

• Frustum,a solid having trapezoidal faces
• Polite number,also known as a trapezoidal number
• Wedge,a polyhedron defined by two triangles and three trapezoid faces.

Further reading

• D. Fraivert, A. Sigler and M. Stupel:Common properties of trapezoids and convex quadrilaterals

External links

• "Trapezium"atEncyclopedia of Mathematics
• Weisstein, Eric W."Right trapezoid".MathWorld.
• Trapezoid definition,Area of a trapezoid,Median of a trapezoid(with interactive animations)
• Trapezoid (North America)at elsy.at: Animated course (construction, circumference, area)
• Trapezoidal RuleonNumerical Methods for Stem Undergraduate
• Autar Kaw and E. Eric Kalu,Numerical Methods with Applications,(2008)