Weak ordering

Not to be confused withWeak order of permutations.

Transitivebinary relations
Symmetric Antisymmetric Connected Well-founded Has joins Has meets Reflexive Irreflexive Asymmetric Total, Semiconnex Anti- reflexive Equivalence relation Y ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Preorder(Quasiorder) ✗ ✗ ✗ ✗ ✗ ✗ Y ✗ ✗ Partial order ✗ Y ✗ ✗ ✗ ✗ Y ✗ ✗ Total preorder ✗ ✗ Y ✗ ✗ ✗ Y ✗ ✗ Total order ✗ Y Y ✗ ✗ ✗ Y ✗ ✗ Prewellordering ✗ ✗ Y Y ✗ ✗ Y ✗ ✗ Well-quasi-ordering ✗ ✗ ✗ Y ✗ ✗ Y ✗ ✗ Well-ordering ✗ Y Y Y ✗ ✗ Y ✗ ✗ Lattice ✗ Y ✗ ✗ Y Y Y ✗ ✗ Join-semilattice ✗ Y ✗ ✗ Y ✗ Y ✗ ✗ Meet-semilattice ✗ Y ✗ ✗ ✗ Y Y ✗ ✗ Strict partial order ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Strict weak order ✗ Y ✗ ✗ ✗ ✗ ✗ Y Y Strict total order ✗ Y Y ✗ ✗ ✗ ✗ Y Y Symmetric Antisymmetric Connected Well-founded Has joins Has meets Reflexive Irreflexive Asymmetric Definitions, for all$a,b$and$S\neq \varnothing:$ ${\begin{aligned}&aRb\\\Rightarrow {}&bRa\end{aligned}}$ ${\begin{aligned}aRb{\text{ and }}&bRa\\\Rightarrow a={}&b\end{aligned}}$ ${\begin{aligned}a\neq {}&b\Rightarrow \\aRb{\text{ or }}&bRa\end{aligned}}$ ${\begin{aligned}\min S\\{\text{exists}}\end{aligned}}$ ${\begin{aligned}a\vee b\\{\text{exists}}\end{aligned}}$ ${\begin{aligned}a\wedge b\\{\text{exists}}\end{aligned}}$ $aRa$ ${\text{not }}aRa$ ${\begin{aligned}aRb\Rightarrow \\{\text{not }}bRa\end{aligned}}$
Yindicates that the column's property is always true the row's term (at the very left), while✗indicates that the property is not guaranteed in general (it might, or might not, hold). For example, that every equivalence relation is symmetric, but not necessarily antisymmetric, is indicated byYin the "Symmetric" column and✗in the "Antisymmetric" column, respectively. All definitions tacitly require thehomogeneous relation$R$betransitive:for all$a,b,c,$if$aRb$and$bRc$then$aRc.$ A term's definition may require additional properties that are not listed in this table.

A weak order on the set$\{a,b,c,d\}$where$a$is ranked below$b$and$c,b$and$c$are of equal rank, and$d$is ranked above$b$and$c$
I) representation as a strict weak order$\,<\,$where$x<y$is shown as an arrow from$x$to$y$;
II) representation as a total preorder$\,\leq,$shown using arrows;
III) representation as an ordered partition, with the sets of the partition as dotted ellipses and the total order on these sets shown with arrows.

The 13 possible strict weak orderings on a set of three elements$\{a,b,c\}.$The onlytotal ordersare shown in black. Two orderings are connected by an edge if they differ by a single dichotomy.

Inmathematics,especiallyorder theory,aweak orderingis a mathematical formalization of the intuitive notion of arankingof aset,some of whose members may betiedwith each other. Weak orders are a generalization oftotally ordered sets(rankings without ties) and are in turn generalized by (strictly)partially ordered setsandpreorders.

There are several common ways of formalizing weak orderings, that are different from each other butcryptomorphic(interconvertable with no loss of information): they may be axiomatized asstrict weak orderings(strictly partially ordered sets in which incomparability is atransitive relation), astotal preorders(transitive binary relations in which at least one of the two possible relations exists between every pair of elements), or asordered partitions(partitionsof the elements into disjoint subsets, together with a total order on the subsets). In many cases another representation called apreferential arrangementbased on autility functionis also possible.

Weak orderings are counted by theordered Bell numbers.They are used incomputer scienceas part ofpartition refinementalgorithms, and in theC++ Standard Library.

Examples

Inhorse racing,the use ofphoto finisheshas eliminated some, but not all, ties or (as they are called in this context)dead heats,so the outcome of a horse race may be modeled by a weak ordering.In an example from theMaryland Hunt Cupsteeplechase in 2007, The Bruce was the clear winner, but two horses Bug River and Lear Charm tied for second place, with the remaining horses farther back; three horses did not finish.In the weak ordering describing this outcome, The Bruce would be first, Bug River and Lear Charm would be ranked after The Bruce but before all the other horses that finished, and the three horses that did not finish would be placed last in the order but tied with each other.

The points of theEuclidean planemay be ordered by theirdistancefrom theorigin,giving another example of a weak ordering with infinitely many elements, infinitely many subsets of tied elements (the sets of points that belong to a commoncirclecentered at the origin), and infinitely many points within these subsets. Although this ordering has a smallest element (the origin itself), it does not have any second-smallest elements, nor any largest element.

Opinion pollingin political elections provides an example of a type of ordering that resembles weak orderings, but is better modeled mathematically in other ways. In the results of a poll, one candidate may be clearly ahead of another, or the two candidates may be statistically tied, meaning not that their poll results are equal but rather that they are within themargin of errorof each other. However, if candidate$x$is statistically tied with$y,$and$y$is statistically tied with$z,$it might still be possible for$x$to be clearly better than$z,$so being tied is not in this case atransitive relation.Because of this possibility, rankings of this type are better modeled assemiordersthan as weak orderings.

Axiomatizations

Suppose throughout that$\,<\,$is ahomogeneousbinary relationon a set$S$(that is,$\,<\,$is a subset of$S\times S$) and as usual, write$x<y$and say that$x<y$holdsoris trueif and only if$(x,y)\in \,<.\,$

Strict weak orderings

Preliminaries on incomparability and transitivity of incomparability

Two elements$x$and$y$of$S$are said to beincomparablewith respect to$\,<\,$if neither$x<y$nor$y<x$is true. Astrict partial order$\,<\,$is a strict weak ordering if and only if incomparability with respect to$\,<\,$is anequivalence relation. Incomparability with respect to$\,<\,$is always a homogeneoussymmetric relationon$S.$ It isreflexiveif and only if$\,<\,$isirreflexive(meaning that$x<x$is always false), which will be assumed so thattransitivityis the only property this "incomparability relation" needs in order to be anequivalence relation.

Define also an induced homogeneous relation$\,\lesssim \,$on$S$by declaring that $$x\lesssim y{\text{ is true }}\quad {\text{ if and only if }}\quad y<x{\text{ is false}}$$ where importantly, this definition isnotnecessarily the same as:$x\lesssim y$if and only if$x<y{\text{ or }}x=y.$ Two elements$x,y\in S$are incomparable with respect to$\,<\,$if and only if$x{\text{ and }}y$areequivalentwith respect to$\,\lesssim \,$(or less verbosely,$\,\lesssim$-equivalent), which by definition means that both$x\lesssim y{\text{ and }}y\lesssim x$are true. The relation "are incomparable with respect to$\,<$"is thus identical to (that is, equal to) the relation" are$\,\lesssim$-equivalent "(so in particular, the former is transitive if and only if the latter is). When$\,<\,$is irreflexive then the property known as "transitivity of incomparability"(defined below) isexactlythe condition necessary and sufficient to guarantee that the relation "are$\,\lesssim$-equivalent "does indeed form an equivalence relation on$S.$ When this is the case, it allows any two elements$x,y\in S$satisfying$x\lesssim y{\text{ and }}y\lesssim x$to be identified as a single object (specifically, they are identified together in their commonequivalence class).

Definition

Astrict weak orderingon a set$S$is astrict partial order$\,<\,$on$S$for which theincomparability relationinduced on$S$by$\,<\,$is atransitive relation. Explicitly, a strict weak order on$S$is ahomogeneous relation$\,<\,$on$S$that has all four of the following properties:

1. Irreflexivity:For all$x\in S,$it is not true that$x<x.$
   • This condition holds if and only if the induced relation$\,\lesssim \,$on$S$isreflexive,where$\,\lesssim \,$is defined by declaring that$x\lesssim y$is true if and only if$y<x$isfalse.
2. Transitivity:For all$x,y,z\in S,$if$x<y{\text{ and }}y<z$then$x<z.$
3. Asymmetry:For all$x,y\in S,$if$x<y$is true then$y<x$is false.
4. Transitivity of incomparability:For all$x,y,z\in S,$if$x$is incomparable with$y$(meaning that neither$x<y$nor$y<x$is true) and if$y$is incomparable with$z,$then$x$is incomparable with$z.$
   • Two elements$x{\text{ and }}y$are incomparable with respect to$\,<\,$if and only if they are equivalent with respect to the induced relation$\,\lesssim \,$(which by definition means that$x\lesssim y{\text{ and }}y\lesssim x$are both true), where as before,$x\lesssim y$is declared to be true if and only if$y<x$is false. Thus this condition holds if and only if thesymmetric relationon$S$defined by "$x{\text{ and }}y$are equivalent with respect to$\,\lesssim \,$"is a transitive relation, meaning that whenever$x{\text{ and }}y$are$\,\lesssim$-equivalent and also$y{\text{ and }}z$are$\,\lesssim$-equivalent then necessarily$x{\text{ and }}z$are$\,\lesssim$-equivalent. This can also be restated as: whenever$x\lesssim y{\text{ and }}y\lesssim x$and also$y\lesssim z{\text{ and }}z\lesssim y$then necessarily$x\lesssim z{\text{ and }}z\lesssim x.$

Properties (1), (2), and (3) are the defining properties of a strict partial order, although there is some redundancy in this list as asymmetry (3) implies irreflexivity (1), and also because irreflexivity (1) and transitivity (2) together imply asymmetry (3).The incomparability relation is alwayssymmetricand it will bereflexiveif and only if$\,<\,$is an irreflexive relation (which is assumed by the above definition). Consequently, a strict partial order$\,<\,$is a strict weak order if and only if its induced incomparability relation is anequivalence relation. In this case, itsequivalence classespartition$S$and moreover, the set${\mathcal {P}}$of these equivalence classes can bestrictly totally orderedby abinary relation,also denoted by$\,<,$that is defined for all$A,B\in {\mathcal {P}}$by:

$A<B{\text{ if and only if }}a<b$for some (or equivalently, for all) representatives$a\in A{\text{ and }}b\in B.$

Conversely, anystrict total orderon apartition${\mathcal {P}}$of$S$gives rise to a strict weak ordering$\,<\,$on$S$defined by$a<b$if and only if there exists sets$A,B\in {\mathcal {P}}$in this partition such that$a\in A,b\in B,{\text{ and }}A<B.$

Not every partial order obeys the transitive law for incomparability. For instance, consider the partial order in the set$\{a,b,c\}$defined by the relationship$b<c.$The pairs$a,b{\text{ and }}a,c$are incomparable but$b$and$c$are related, so incomparability does not form an equivalence relation and this example is not a strict weak ordering.

For transitivity of incomparability, each of the following conditions isnecessary,and for strict partial orders alsosufficient:

• If$x<y$then for all$z,$either$x<z{\text{ or }}z<y$or both.
• If$x$is incomparable with$y$then for all$z$,either ($x<z{\text{ and }}y<z$) or ($z<x{\text{ and }}z<y$) or ($z$is incomparable with$x$and$z$is incomparable with$y$).

Total preorders

Strict weak orders are very closely related tototal preordersor(non-strict) weak orders,and the same mathematical concepts that can be modeled with strict weak orderings can be modeled equally well with total preorders. A total preorder or weak order is apreorderin which any two elements are comparable.A total preorder$\,\lesssim \,$satisfies the following properties:

• Transitivity:For all$x,y,{\text{ and }}z,$if$x\lesssim y{\text{ and }}y\lesssim z$then$x\lesssim z.$
• Strong connectedness:For all$x{\text{ and }}y,$$x\lesssim y{\text{ or }}y\lesssim x.$
  • Which impliesreflexivity:for all$x,$$x\lesssim x.$

Atotal orderis a total preorder which is antisymmetric, in other words, which is also apartial order.Total preorders are sometimes also calledpreference relations.

Thecomplementof a strict weak order is a total preorder, and vice versa, but it seems more natural to relate strict weak orders and total preorders in a way that preserves rather than reverses the order of the elements. Thus we take theconverseof the complement: for a strict weak ordering$\,<,$define a total preorder$\,\lesssim \,$by setting$x\lesssim y$whenever it is not the case that$y<x.$In the other direction, to define a strict weak ordering < from a total preorder$\,\lesssim,$set$x<y$whenever it is not the case that$y\lesssim x.$

In any preorder there is acorresponding equivalence relationwhere two elements$x$and$y$are defined asequivalentif$x\lesssim y{\text{ and }}y\lesssim x.$In the case of atotalpreorder the corresponding partial order on the set of equivalence classes is a total order. Two elements are equivalent in a total preorder if and only if they are incomparable in the corresponding strict weak ordering.

Ordered partitions

Apartition of a set$S$is a family of non-empty disjoint subsets of$S$that have$S$as their union. A partition, together with atotal orderon the sets of the partition, gives a structure called byRichard P. Stanleyanordered partitionand byTheodore Motzkinalist of sets.An ordered partition of a finite set may be written as afinite sequenceof the sets in the partition: for instance, the three ordered partitions of the set$\{a,b\}$are $$\{a\},\{b\},$$ $$\{b\},\{a\},\;{\text{ and }}$$ $$\{a,b\}.$$

In a strict weak ordering, the equivalence classes of incomparability give a set partition, in which the sets inherit a total ordering from their elements, giving rise to an ordered partition. In the other direction, any ordered partition gives rise to a strict weak ordering in which two elements are incomparable when they belong to the same set in the partition, and otherwise inherit the order of the sets that contain them.

Representation by functions

For sets of sufficiently smallcardinality,a fourth axiomatization is possible, based on real-valued functions. If$X$is any set then a real-valued function$f:X\to \mathbb {R}$on$X$induces a strict weak order on$X$by setting $$a<b{\text{ if and only if }}f(a)<f(b).$$ The associated total preorder is given by setting $a{}\lesssim {}b{\text{ if and only if }}f(a)\leq f(b)$ and the associated equivalence by setting $a{}\sim {}b{\text{ if and only if }}f(a)=f(b).$

The relations do not change when$f$is replaced by$g\circ f$(composite function), where$g$is astrictly increasingreal-valued function defined on at least the range of$f.$Thus for example, autility functiondefines apreferencerelation. In this context, weak orderings are also known aspreferential arrangements.

If$X$is finite or countable, every weak order on$X$can be represented by a function in this way.However, there exist strict weak orders that have no corresponding real function. For example, there is no such function for thelexicographic orderon$\mathbb {R} ^{n}.$Thus, while in most preference relation models the relation defines a utility functionup toorder-preserving transformations, there is no such function forlexicographic preferences.

More generally, if$X$is a set,$Y$is a set with a strict weak ordering$\,<,\,$and$f:X\to Y$is a function, then$f$induces a strict weak ordering on$X$by setting $$a<b{\text{ if and only if }}f(a)<f(b).$$ As before, the associated total preorder is given by setting $a{}\lesssim {}b{\text{ if and only if }}f(a){}\lesssim {}f(b),$ and the associated equivalence by setting $a{}\sim {}b{\text{ if and only if }}f(a){}\sim {}f(b).$ It is not assumed here that$f$is aninjective function,so a class of two equivalent elements on$Y$may induce a larger class of equivalent elements on$X.$Also,$f$is not assumed to be asurjective function,so a class of equivalent elements on$Y$may induce a smaller or empty class on$X.$However, the function$f$induces an injective function that maps the partition on$X$to that on$Y.$Thus, in the case of finite partitions, the number of classes in$X$is less than or equal to the number of classes on$Y.$

Related types of ordering

Semiordersgeneralize strict weak orderings, but do not assume transitivity of incomparability.A strict weak order that istrichotomousis called astrict total order.The total preorder which is the inverse of its complement is in this case atotal order.

For a strict weak order$\,<\,$another associated reflexive relation is itsreflexive closure,a (non-strict) partial order$\,\leq.$The two associated reflexive relations differ with regard to different$a$and$b$for which neither$a<b$nor$b<a$:in the total preorder corresponding to a strict weak order we get$a\lesssim b$and$b\lesssim a,$while in the partial order given by the reflexive closure we get neither$a\leq b$nor$b\leq a.$For strict total orders these two associated reflexive relations are the same: the corresponding (non-strict) total order.The reflexive closure of a strict weak ordering is a type ofseries-parallel partial order.

All weak orders on a finite set

Combinatorial enumeration

Main article:ordered Bell number

The number of distinct weak orders (represented either as strict weak orders or as total preorders) on an$n$-element set is given by the following sequence (sequenceA000670in theOEIS):

Number ofn-element binary relations of different types

Elem­ents	Any	Transitive	Reflexive	Symmetric	Preorder	Partial order	Total preorder	Total order	Equivalence relation
0	1	1	1	1	1	1	1	1	1
1	2	2	1	2	1	1	1	1	1
2	16	13	4	8	4	3	3	2	2
3	512	171	64	64	29	19	13	6	5
4	65,536	3,994	4,096	1,024	355	219	75	24	15
n	2n2		2n(n−1)	2n(n+1)/2			∑n k=0k!S(n,k)	n!	∑n k=0S(n,k)
OEIS	A002416	A006905	A053763	A006125	A000798	A001035	A000670	A000142	A000110

Note thatS(n,k)refers toStirling numbers of the second kind.

These numbers are also called theFubini numbersorordered Bell numbers.

For example, for a set of three labeled items, there is one weak order in which all three items are tied. There are three ways of partitioning the items into onesingletonset and one group of two tied items, and each of these partitions gives two weak orders (one in which the singleton is smaller than the group of two, and one in which this ordering is reversed), giving six weak orders of this type. And there is a single way of partitioning the set into three singletons, which can be totally ordered in six different ways. Thus, altogether, there are 13 different weak orders on three items.

Adjacency structure

The permutohedron on four elements, a three-dimensionalconvex polyhedron.It has 24 vertices, 36 edges, and 14 two-dimensional faces, which all together with the whole three-dimensional polyhedron correspond to the 75 weak orderings on four elements.

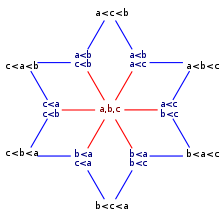
Unlike for partial orders, the family of weak orderings on a given finite set is not in general connected by moves that add or remove a single order relation to or from a given ordering. For instance, for three elements, the ordering in which all three elements are tied differs by at least two pairs from any other weak ordering on the same set, in either the strict weak ordering or total preorder axiomatizations. However, a different kind of move is possible, in which the weak orderings on a set are more highly connected. Define adichotomyto be a weak ordering with two equivalence classes, and define a dichotomy to becompatiblewith a given weak ordering if every two elements that are related in the ordering are either related in the same way or tied in the dichotomy. Alternatively, a dichotomy may be defined as aDedekind cutfor a weak ordering. Then a weak ordering may be characterized by its set of compatible dichotomies. For a finite set of labeled items, every pair of weak orderings may be connected to each other by a sequence of moves that add or remove one dichotomy at a time to or from this set of dichotomies. Moreover, theundirected graphthat has the weak orderings as its vertices, and these moves as its edges, forms apartial cube.

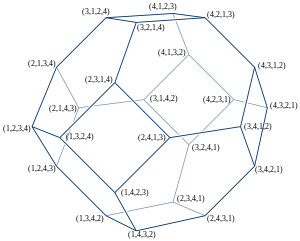
Geometrically, the total orderings of a given finite set may be represented as the vertices of apermutohedron,and the dichotomies on this same set as the facets of the permutohedron. In this geometric representation, the weak orderings on the set correspond to the faces of all different dimensions of the permutohedron (including the permutohedron itself, but not the empty set, as a face). Thecodimensionof a face gives the number of equivalence classes in the corresponding weak ordering.In this geometric representation the partial cube of moves on weak orderings is the graph describing thecovering relationof theface latticeof the permutohedron.

For instance, for$n=3,$the permutohedron on three elements is just a regular hexagon. The face lattice of the hexagon (again, including the hexagon itself as a face, but not including the empty set) has thirteen elements: one hexagon, six edges, and six vertices, corresponding to the one completely tied weak ordering, six weak orderings with one tie, and six total orderings. The graph of moves on these 13 weak orderings is shown in the figure.

Applications

As mentioned above, weak orders have applications in utility theory.Inlinear programmingand other types ofcombinatorial optimizationproblem, the prioritization of solutions or of bases is often given by a weak order, determined by a real-valuedobjective function;the phenomenon of ties in these orderings is called "degeneracy", and several types of tie-breaking rule have been used to refine this weak ordering into a total ordering in order to prevent problems caused by degeneracy.

Weak orders have also been used incomputer science,inpartition refinementbased algorithms forlexicographic breadth-first searchandlexicographic topological ordering.In these algorithms, a weak ordering on the vertices of a graph (represented as a family of sets thatpartitionthe vertices, together with adoubly linked listproviding a total order on the sets) is gradually refined over the course of the algorithm, eventually producing a total ordering that is the output of the algorithm.

In theStandard Libraryfor theC++programming language, theset and multiset data typessort their input by a comparison function that is specified at the time of template instantiation, and that is assumed to implement a strict weak ordering.

See also

• Comparability– Property of elements related by inequalities
• Preorder– Reflexive and transitive binary relation
• Weak component– Partition of vertices of a directed graph − the equivalent subsets in the finest weak ordering consistent with a given relation