Convex function

Convex function on aninterval.

A function (in black) is convex if and only if the region above itsgraph(in green) is aconvex set.

A graph of thebivariateconvex functionx²+xy+y².

Convex vs. Not convex

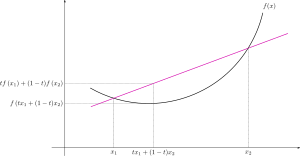
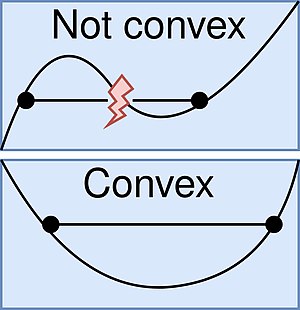
Inmathematics,areal-valued functionis calledconvexif theline segmentbetween any two distinct points on thegraph of the functionlies above the graph between the two points. Equivalently, a function is convex if itsepigraph(the set of points on or above the graph of the function) is aconvex set. In simple terms, a convex function graph is shaped like a cup$\cup$(or a straight line like a linear function), while aconcave function's graph is shaped like a cap$\cap$.

A twice-differentiablefunction of a single variable is convexif and only ifitssecond derivativeis nonnegative on its entiredomain.Well-known examples of convex functions of a single variable include alinear function$f(x)=cx$(where$c$is areal number), aquadratic function$cx^{2}$($c$as a nonnegative real number) and anexponential function$ce^{x}$($c$as a nonnegative real number).

Convex functions play an important role in many areas of mathematics. They are especially important in the study ofoptimizationproblems where they are distinguished by a number of convenient properties. For instance, a strictly convex function on anopen sethas no more than oneminimum.Even in infinite-dimensional spaces, under suitable additional hypotheses, convex functions continue to satisfy such properties and as a result, they are the most well-understood functionals in thecalculus of variations.Inprobability theory,a convex function applied to theexpected valueof arandom variableis always bounded above by the expected value of the convex function of the random variable. This result, known asJensen's inequality,can be used to deduceinequalitiessuch as thearithmetic–geometric mean inequalityandHölder's inequality.

Definition

Visualizing a convex function and Jensen's Inequality

Let$X$be aconvex subsetof a realvector spaceand let$f:X\to \mathbb {R}$be a function.

Then$f$is calledconvexif and only if any of the following equivalent conditions hold:

1. For all$0\leq t\leq 1$and all$x_{1},x_{2}\in X$:
   $$f\left(tx_{1}+(1-t)x_{2}\right)\leq tf\left(x_{1}\right)+(1-t)f\left(x_{2}\right)$$
   The right hand side represents the straight line between$\left(x_{1},f\left(x_{1}\right)\right)$and$\left(x_{2},f\left(x_{2}\right)\right)$in the graph of$f$as a function of$t;$increasing$t$from$0$to$1$or decreasing$t$from$1$to$0$sweeps this line. Similarly, the argument of the function$f$in the left hand side represents the straight line between$x_{1}$and$x_{2}$in$X$or the$x$-axis of the graph of$f.$So, this condition requires that the straight line between any pair of points on the curve of$f$to be above or just meets the graph.
2. For all$0<t<1$and all$x_{1},x_{2}\in X$such that$x_{1}\neq x_{2}$:
   $$f\left(tx_{1}+(1-t)x_{2}\right)\leq tf\left(x_{1}\right)+(1-t)f\left(x_{2}\right)$$
   The difference of this second condition with respect to the first condition above is that this condition does not include the intersection points (for example,$\left(x_{1},f\left(x_{1}\right)\right)$and$\left(x_{2},f\left(x_{2}\right)\right)$) between the straight line passing through a pair of points on the curve of$f$(the straight line is represented by the right hand side of this condition) and the curve of$f;$the first condition includes the intersection points as it becomes$f\left(x_{1}\right)\leq f\left(x_{1}\right)$or$f\left(x_{2}\right)\leq f\left(x_{2}\right)$at$t=0$or$1,$or$x_{1}=x_{2}.$In fact, the intersection points do not need to be considered in a condition of convex using
   $$f\left(tx_{1}+(1-t)x_{2}\right)\leq tf\left(x_{1}\right)+(1-t)f\left(x_{2}\right)$$
   because$f\left(x_{1}\right)\leq f\left(x_{1}\right)$and$f\left(x_{2}\right)\leq f\left(x_{2}\right)$are always true (so not useful to be a part of a condition).

The second statement characterizing convex functions that are valued in the real line$\mathbb {R}$is also the statement used to defineconvex functionsthat are valued in theextended real number line$[-\infty,\infty ]=\mathbb {R} \cup \{\pm \infty \},$where such a function$f$is allowed to take$\pm \infty$as a value. The first statement is not used because it permits$t$to take$0$or$1$as a value, in which case, if$f\left(x_{1}\right)=\pm \infty$or$f\left(x_{2}\right)=\pm \infty,$respectively, then$tf\left(x_{1}\right)+(1-t)f\left(x_{2}\right)$would be undefined (because the multiplications$0\cdot \infty$and$0\cdot (-\infty )$are undefined). The sum$-\infty +\infty$is also undefined so a convex extended real-valued function is typically only allowed to take exactly one of$-\infty$and$+\infty$as a value.

The second statement can also be modified to get the definition ofstrict convexity,where the latter is obtained by replacing$\,\leq \,$with the strict inequality$\,<.$ Explicitly, the map$f$is calledstrictly convexif and only if for all real$0<t<1$and all$x_{1},x_{2}\in X$such that$x_{1}\neq x_{2}$:

$$f\left(tx_{1}+(1-t)x_{2}\right)<tf\left(x_{1}\right)+(1-t)f\left(x_{2}\right)$$

A strictly convex function$f$is a function that the straight line between any pair of points on the curve$f$is above the curve$f$except for the intersection points between the straight line and the curve. An example of a function which is convex but not strictly convex is$f(x,y)=x^{2}+y$.This function is not strictly convex because any two points sharing an x coordinate will have a straight line between them, while any two points NOT sharing an x coordinate will have a greater value of the function than the points between them.

The function$f$is said to beconcave(resp.strictly concave) if$-f$($f$multiplied by −1) is convex (resp. strictly convex).

Alternative naming

The termconvexis often referred to asconvex downorconcave upward,and the termconcaveis often referred asconcave downorconvex upward.If the term "convex" is used without an "up" or "down" keyword, then it refers strictly to a cup shaped graph$\cup$.As an example,Jensen's inequalityrefers to an inequality involving a convex or convex-(down), function.

Properties

Many properties of convex functions have the same simple formulation for functions of many variables as for functions of one variable. See below the properties for the case of many variables, as some of them are not listed for functions of one variable.

Functions of one variable

• Suppose$f$is a function of onerealvariable defined on an interval, and let
  $$R(x_{1},x_{2})={\frac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}$$
  (note that$R(x_{1},x_{2})$is the slope of the purple line in the first drawing; the function$R$issymmetricin$(x_{1},x_{2}),$means that$R$does not change by exchanging$x_{1}$and$x_{2}$).$f$is convex if and only if$R(x_{1},x_{2})$ismonotonically non-decreasingin$x_{1},$for every fixed$x_{2}$(or vice versa). This characterization of convexity is quite useful to prove the following results.
• A convex function$f$of one real variable defined on someopen interval$C$iscontinuouson$C.$$f$admitsleft and right derivatives,and these aremonotonically non-decreasing.In addition, the left derivative is left-continuous and the right-derivative is right-continuous. As a consequence,$f$isdifferentiableat all but at mostcountably manypoints, the set on which$f$is not differentiable can however still be dense. If$C$is closed, then$f$may fail to be continuous at the endpoints of$C$(an example is shown in theexamples section).
• Adifferentiablefunction of one variable is convex on an interval if and only if itsderivativeismonotonically non-decreasingon that interval. If a function is differentiable and convex then it is alsocontinuously differentiable.
• A differentiable function of one variable is convex on an interval if and only if its graph lies above all of itstangents:
  $$f(x)\geq f(y)+f'(y)(x-y)$$
  for all$x$and$y$in the interval.
• A twice differentiable function of one variable is convex on an interval if and only if itssecond derivativeis non-negative there; this gives a practical test for convexity. Visually, a twice differentiable convex function "curves up", without any bends the other way (inflection points). If its second derivative is positive at all points then the function is strictly convex, but theconversedoes not hold. For example, the second derivative of$f(x)=x^{4}$is$f''(x)=12x^{2}$,which is zero for$x=0,$but$x^{4}$is strictly convex.
  • This property and the above property in terms of "...its derivative is monotonically non-decreasing..." are not equal since if$f''$is non-negative on an interval$X$then$f'$is monotonically non-decreasing on$X$while its converse is not true, for example,$f'$is monotonically non-decreasing on$X$while its derivative$f''$is not defined at some points on$X$.
• If$f$is a convex function of one real variable, and$f(0)\leq 0$,then$f$issuperadditiveon thepositive reals,that is$f(a+b)\geq f(a)+f(b)$for positive real numbers$a$and$b$.

Proof

Since$f$is convex, by using one of the convex function definitions above and letting$x_{2}=0,$it follows that for all real$0\leq t\leq 1,$

$${\begin{aligned}f(tx_{1})&=f(tx_{1}+(1-t)\cdot 0)\\&\leq tf(x_{1})+(1-t)f(0)\\&\leq tf(x_{1}).\\\end{aligned}}$$

From$f(tx_{1})\leq tf(x_{1})$,it follows that

$${\begin{aligned}f(a)+f(b)&=f\left((a+b){\frac {a}{a+b}}\right)+f\left((a+b){\frac {b}{a+b}}\right)\\&\leq {\frac {a}{a+b}}f(a+b)+{\frac {b}{a+b}}f(a+b)\\&=f(a+b).\\\end{aligned}}$$

Namely,$f(a)+f(b)\leq f(a+b)$.

• A function$f$is midpoint convex on an interval$C$if for all$x_{1},x_{2}\in C$
  $$f\!\left({\frac {x_{1}+x_{2}}{2}}\right)\leq {\frac {f(x_{1})+f(x_{2})}{2}}.$$
  This condition is only slightly weaker than convexity. For example, a real-valuedLebesgue measurable functionthat is midpoint-convex is convex: this is a theorem ofSierpiński.In particular, a continuous function that is midpoint convex will be convex.

Functions of several variables

• A function that is marginally convex in each individual variable is not necessarily (jointly) convex. For example, the function$f(x,y)=xy$ismarginally linear,and thus marginally convex, in each variable, but not (jointly) convex.
• A function$f:X\to [-\infty,\infty ]$valued in theextended real numbers$[-\infty,\infty ]=\mathbb {R} \cup \{\pm \infty \}$is convex if and only if itsepigraph
  $$\{(x,r)\in X\times \mathbb {R} ~:~r\geq f(x)\}$$
  is a convex set.
• A differentiable function$f$defined on a convex domain is convex if and only if$f(x)\geq f(y)+\nabla f(y)^{T}\cdot (x-y)$holds for all$x,y$in the domain.
• A twice differentiable function of several variables is convex on a convex set if and only if itsHessian matrixof secondpartial derivativesispositive semidefiniteon the interior of the convex set.
• For a convex function$f,$thesublevel sets$\{x:f(x)<a\}$and$\{x:f(x)\leq a\}$with$a\in \mathbb {R}$are convex sets. A function that satisfies this property is called aquasiconvex functionand may fail to be a convex function.
• Consequently, the set ofglobal minimisersof a convex function$f$is a convex set:${\operatorname {argmin} }\,f$- convex.
• Anylocal minimumof a convex function is also aglobal minimum.Astrictlyconvex function will have at most one global minimum.
• Jensen's inequalityapplies to every convex function$f$.If$X$is a random variable taking values in the domain of$f,$then$\operatorname {E} (f(X))\geq f(\operatorname {E} (X)),$where$\operatorname {E}$denotes themathematical expectation.Indeed, convex functions are exactly those that satisfies the hypothesis ofJensen's inequality.
• A first-orderhomogeneous functionof two positive variables$x$and$y,$(that is, a function satisfying$f(ax,ay)=af(x,y)$for all positive real$a,x,y>0$) that is convex in one variable must be convex in the other variable.

Operations that preserve convexity

• $-f$is concave if and only if$f$is convex.
• If$r$is any real number then$r+f$is convex if and only if$f$is convex.
• Nonnegative weighted sums:
  • if$w_{1},\ldots,w_{n}\geq 0$and$f_{1},\ldots,f_{n}$are all convex, then so is$w_{1}f_{1}+\cdots +w_{n}f_{n}.$In particular, the sum of two convex functions is convex.
  • this property extends to infinite sums, integrals and expected values as well (provided that they exist).
• Elementwise maximum: let$\{f_{i}\}_{i\in I}$be a collection of convex functions. Then$g(x)=\sup \nolimits _{i\in I}f_{i}(x)$is convex. The domain of$g(x)$is the collection of points where the expression is finite. Important special cases:
  • If$f_{1},\ldots,f_{n}$are convex functions then so is$g(x)=\max \left\{f_{1}(x),\ldots,f_{n}(x)\right\}.$
  • Danskin's theorem:If$f(x,y)$is convex in$x$then$g(x)=\sup \nolimits _{y\in C}f(x,y)$is convex in$x$even if$C$is not a convex set.
• Composition:
  • If$f$and$g$are convex functions and$g$is non-decreasing over a univariate domain, then$h(x)=g(f(x))$is convex. For example, if$f$is convex, then so is$e^{f(x)}$because$e^{x}$is convex and monotonically increasing.
  • If$f$is concave and$g$is convex and non-increasing over a univariate domain, then$h(x)=g(f(x))$is convex.
  • Convexity is invariant under affine maps: that is, if$f$is convex with domain$D_{f}\subseteq \mathbf {R} ^{m}$,then so is$g(x)=f(Ax+b)$,where$A\in \mathbf {R} ^{m\times n},b\in \mathbf {R} ^{m}$with domain$D_{g}\subseteq \mathbf {R} ^{n}.$
• Minimization: If$f(x,y)$is convex in$(x,y)$then$g(x)=\inf \nolimits _{y\in C}f(x,y)$is convex in$x,$provided that$C$is a convex set and that$g(x)\neq -\infty.$
• If$f$is convex, then its perspective$g(x,t)=tf\left({\tfrac {x}{t}}\right)$with domain$\left\{(x,t):{\tfrac {x}{t}}\in \operatorname {Dom} (f),t>0\right\}$is convex.
• Let$X$be a vector space.$f:X\to \mathbf {R}$is convex and satisfies$f(0)\leq 0$if and only if$f(ax+by)\leq af(x)+bf(y)$for any$x,y\in X$and any non-negative real numbers$a,b$that satisfy$a+b\leq 1.$

Strongly convex functions

The concept of strong convexity extends and parametrizes the notion of strict convexity. Intuitively, a strongly-convex function is a function that grows as fast as a quadratic function.A strongly convex function is also strictly convex, but not vice versa. If a one-dimensional function$f$is twice continuously differentiable and the domain is the real line, then we can characterize it as follows:

• $f$convex if and only if$f''(x)\geq 0$for all$x.$
• $f$strictly convex if$f''(x)>0$for all$x$(note: this is sufficient, but not necessary).
• $f$strongly convex if and only if$f''(x)\geq m>0$for all$x.$

For example, let$f$be strictly convex, and suppose there is a sequence of points$(x_{n})$such that$f''(x_{n})={\tfrac {1}{n}}$.Even though$f''(x_{n})>0$,the function is not strongly convex because$f''(x)$will become arbitrarily small.

More generally, a differentiable function$f$is called strongly convex with parameter$m>0$if the following inequality holds for all points$x,y$in its domain:

$$(\nabla f(x)-\nabla f(y))^{T}(x-y)\geq m\|x-y\|_{2}^{2}$$

or, more generally,

$$\langle \nabla f(x)-\nabla f(y),x-y\rangle \geq m\|x-y\|^{2}$$

where$\langle \cdot,\cdot \rangle$is anyinner product,and$\|\cdot \|$is the correspondingnorm.Some authors, such asrefer to functions satisfying this inequality asellipticfunctions.

An equivalent condition is the following:

$$f(y)\geq f(x)+\nabla f(x)^{T}(y-x)+{\frac {m}{2}}\|y-x\|_{2}^{2}$$

It is not necessary for a function to be differentiable in order to be strongly convex. A third definitionfor a strongly convex function, with parameter$m,$is that, for all$x,y$in the domain and$t\in [0,1],$

$$f(tx+(1-t)y)\leq tf(x)+(1-t)f(y)-{\frac {1}{2}}mt(1-t)\|x-y\|_{2}^{2}$$

Notice that this definition approaches the definition for strict convexity as$m\to 0,$and is identical to the definition of a convex function when$m=0.$Despite this, functions exist that are strictly convex but are not strongly convex for any$m>0$(see example below).

If the function$f$is twice continuously differentiable, then it is strongly convex with parameter$m$if and only if$\nabla ^{2}f(x)\succeq mI$for all$x$in the domain, where$I$is the identity and$\nabla ^{2}f$is theHessian matrix,and the inequality$\succeq$means that$\nabla ^{2}f(x)-mI$ispositive semi-definite.This is equivalent to requiring that the minimumeigenvalueof$\nabla ^{2}f(x)$be at least$m$for all$x.$If the domain is just the real line, then$\nabla ^{2}f(x)$is just the second derivative$f''(x),$so the condition becomes$f''(x)\geq m$.If$m=0$then this means the Hessian is positive semidefinite (or if the domain is the real line, it means that$f''(x)\geq 0$), which implies the function is convex, and perhaps strictly convex, but not strongly convex.

Assuming still that the function is twice continuously differentiable, one can show that the lower bound of$\nabla ^{2}f(x)$implies that it is strongly convex. UsingTaylor's Theoremthere exists

$$z\in \{tx+(1-t)y:t\in [0,1]\}$$

such that

$$f(y)=f(x)+\nabla f(x)^{T}(y-x)+{\frac {1}{2}}(y-x)^{T}\nabla ^{2}f(z)(y-x)$$

Then

$$(y-x)^{T}\nabla ^{2}f(z)(y-x)\geq m(y-x)^{T}(y-x)$$

by the assumption about the eigenvalues, and hence we recover the second strong convexity equation above.

A function$f$is strongly convex with parametermif and only if the function

$$x\mapsto f(x)-{\frac {m}{2}}\|x\|^{2}$$

is convex.

A twice continuously differentiable function$f$on a compact domain$X$that satisfies$f''(x)>0$for all$x\in X$is strongly convex. The proof of this statement follows from theextreme value theorem,which states that a continuous function on a compact set has a maximum and minimum.

Strongly convex functions are in general easier to work with than convex or strictly convex functions, since they are a smaller class. Like strictly convex functions, strongly convex functions have unique minima on compact sets.

Properties of strongly-convex functions

Iffis a strongly-convex function with parameterm,then:

• For every real numberr,thelevel set{x|f(x) ≤r} iscompact.
• The functionfhas a uniqueglobal minimumonRⁿ.

Uniformly convex functions

A uniformly convex function,with modulus$\phi$,is a function$f$that, for all$x,y$in the domain and$t\in [0,1],$satisfies

$$f(tx+(1-t)y)\leq tf(x)+(1-t)f(y)-t(1-t)\phi (\|x-y\|)$$

where$\phi$is a function that is non-negative and vanishes only at 0. This is a generalization of the concept of strongly convex function; by taking$\phi (\alpha )={\tfrac {m}{2}}\alpha ^{2}$we recover the definition of strong convexity.

It is worth noting that some authors require the modulus$\phi$to be an increasing function,but this condition is not required by all authors.

Examples

Functions of one variable

• The function$f(x)=x^{2}$has$f''(x)=2>0$,sofis a convex function. It is also strongly convex (and hence strictly convex too), with strong convexity constant 2.
• The function$f(x)=x^{4}$has$f''(x)=12x^{2}\geq 0$,sofis a convex function. It is strictly convex, even though the second derivative is not strictly positive at all points. It is not strongly convex.
• Theabsolute valuefunction$f(x)=|x|$is convex (as reflected in thetriangle inequality), even though it does not have a derivative at the point$x=0.$It is not strictly convex.
• The function$f(x)=|x|^{p}$for$p\geq 1$is convex.
• Theexponential function$f(x)=e^{x}$is convex. It is also strictly convex, since$f''(x)=e^{x}>0$,but it is not strongly convex since the second derivative can be arbitrarily close to zero. More generally, the function$g(x)=e^{f(x)}$islogarithmically convexif$f$is a convex function. The term "superconvex" is sometimes used instead.
• The function$f$with domain [0,1] defined by$f(0)=f(1)=1,f(x)=0$for$0<x<1$is convex; it is continuous on the open interval$(0,1),$but not continuous at 0 and 1.
• The function$x^{3}$has second derivative$6x$;thus it is convex on the set where$x\geq 0$andconcaveon the set where$x\leq 0.$
• Examples of functions that aremonotonically increasingbut not convex include$f(x)={\sqrt {x}}$and$g(x)=\log x$.
• Examples of functions that are convex but notmonotonically increasinginclude$h(x)=x^{2}$and$k(x)=-x$.
• The function$f(x)={\tfrac {1}{x}}$has$f''(x)={\tfrac {2}{x^{3}}}$which is greater than 0 if$x>0$so$f(x)$is convex on the interval$(0,\infty )$.It is concave on the interval$(-\infty,0)$.
• The function$f(x)={\tfrac {1}{x^{2}}}$with$f(0)=\infty$,is convex on the interval$(0,\infty )$and convex on the interval$(-\infty,0)$,but not convex on the interval$(-\infty,\infty )$,because of the singularity at$x=0.$

Functions ofnvariables

• LogSumExpfunction, also called softmax function, is a convex function.
• The function$-\log \det(X)$on the domain ofpositive-definite matricesis convex.
• Every real-valuedlinear transformationis convex but not strictly convex, since if$f$is linear, then$f(a+b)=f(a)+f(b)$.This statement also holds if we replace "convex" by "concave".
• Every real-valuedaffine function,that is, each function of the form$f(x)=a^{T}x+b,$is simultaneously convex and concave.
• Everynormis a convex function, by thetriangle inequalityandpositive homogeneity.
• Thespectral radiusof anonnegative matrixis a convex function of its diagonal elements.

See also

• Concave function
• Convex analysis
• Convex conjugate
• Convex curve
• Convex optimization
• Geodesic convexity
• Hahn–Banach theorem
• Hermite–Hadamard inequality
• Invex function
• Jensen's inequality
• K-convex function
• Kachurovskii's theorem,which relates convexity tomonotonicityof the derivative
• Karamata's inequality
• Logarithmically convex function
• Pseudoconvex function
• Quasiconvex function
• Subderivativeof a convex function

References

• Bertsekas, Dimitri(2003).Convex Analysis and Optimization.Athena Scientific.
• Borwein, Jonathan,and Lewis, Adrian. (2000). Convex Analysis and Nonlinear Optimization. Springer.
• Donoghue, William F. (1969).Distributions and Fourier Transforms.Academic Press.
• Hiriart-Urruty, Jean-Baptiste, andLemaréchal, Claude.(2004). Fundamentals of Convex analysis. Berlin: Springer.
• Krasnosel'skii M.A.,Rutickii Ya.B. (1961).Convex Functions and Orlicz Spaces.Groningen: P.Noordhoff Ltd.
• Lauritzen, Niels (2013).Undergraduate Convexity.World Scientific Publishing.
• Luenberger, David(1984).Linear and Nonlinear Programming.Addison-Wesley.
• Luenberger, David(1969).Optimization by Vector Space Methods.Wiley & Sons.
• Rockafellar, R. T.(1970).Convex analysis.Princeton: Princeton University Press.
• Thomson, Brian (1994).Symmetric Properties of Real Functions.CRC Press.
• Zălinescu, C. (2002).Convex analysis in general vector spaces.River Edge, NJ: World Scientific Publishing Co., Inc. pp. xx+367.ISBN981-238-067-1.MR1921556.

External links

• "Convex function (of a real variable)",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• "Convex function (of a complex variable)",Encyclopedia of Mathematics,EMS Press,2001 [1994]