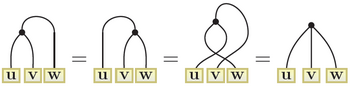Trace diagram

A trace diagram representing theadjugate of a matrix.

Inmathematics,trace diagramsare a graphical means of performing computations inlinearandmultilinear algebra.They can be represented as (slightly modified)graphsin which some edges are labeled bymatrices.The simplest trace diagrams represent thetraceanddeterminantof a matrix. Several results in linear algebra, such asCramer's Ruleand theCayley–Hamilton theorem,have simple diagrammatic proofs. They are closely related toPenrose's graphical notation.

Formal definition

LetVbe avector spaceofdimensionnover afieldF(withn≥2), and let Hom(V,V) denote thelinear transformationsonV.Ann-trace diagramis agraph${\mathcal {D}}=(V_{1}\sqcup V_{2}\sqcup V_{n},E)$,where the setsV_i(i= 1, 2,n) are composed ofverticesofdegreei,together with the following additional structures:

• aciliationat each vertex in the graph, which is an explicit ordering of the adjacent edges at that vertex;
• a labelingV₂→ Hom(V,V) associating each degree-2 vertex to a linear transformation.

Note thatV₂andV_nshould be considered as distinct sets in the casen= 2. Aframed trace diagramis a trace diagram together with a partition of the degree-1 verticesV₁into two disjoint ordered collections called theinputsand theoutputs.

The "graph" underlying a trace diagram may have the following special features, which are not always included in the standard definition of a graph:

• Loopsare permitted (a loop is an edge that connects a vertex to itself).
• Edges that have no vertices are permitted, and are represented by small circles.
• Multiple edges between the same two vertices are permitted.

Drawing conventions

• When trace diagrams are drawn, the ciliation on ann-vertex is commonly represented by a small mark between two of the incident edges (in the figure above, a small red dot); the specific ordering of edges follows by proceeding counter-clockwise from this mark.
• The ciliation and labeling at a degree-2 vertex are combined into a single directed node that allows one to differentiate the first edge (theincomingedge) from the second edge (theoutgoingedge).
• Framed diagrams are drawn withinputsat the bottom of the diagram andoutputsat the top of the diagram. In both cases, the ordering corresponds to reading from left to right.

Correspondence with multilinear functions

Every framed trace diagram corresponds to amultilinearfunction betweentensorpowers of the vector spaceV.The degree-1 vertices correspond to the inputs and outputs of the function, while the degree-nvertices correspond to the generalizedLevi-Civita symbol(which is ananti-symmetric tensorrelated to thedeterminant). If a diagram has no output strands, its function maps tensor products to a scalar. If there are no degree-1 vertices, the diagram is said to beclosedand its corresponding function may be identified with a scalar.

By definition, a trace diagram's function is computed usingsigned graphcoloring. For eachedge coloringof the graph's edges bynlabels, so that no two edges adjacent to the same vertex have the same label, one assigns aweightbased on the labels at the vertices and the labels adjacent to the matrix labels. These weights become the coefficients of the diagram's function.

In practice, a trace diagram's function is typically computed bydecomposingthe diagram into smaller pieces whose functions are known. The overall function can then be computed by re-composing the individual functions.

Examples

3-Vector diagrams

Severalvector identitieshave easy proofs using trace diagrams. This section covers 3-trace diagrams. In the translation of diagrams to functions, it can be shown that the positions of ciliations at the degree-3 vertices has no influence on the resulting function, so they may be omitted.

It can be shown that thecross productanddot productof 3-dimensional vectors are represented by

In this picture, the inputs to the function are shown as vectors in yellow boxes at the bottom of the diagram. The cross product diagram has an output vector, represented by the free strand at the top of the diagram. The dot product diagram does not have an output vector; hence, its output is a scalar.

As a first example, consider the scalar triple product identity

$(\mathbf {u} \times \mathbf {v} )\cdot \mathbf {w} =\mathbf {u} \cdot (\mathbf {v} \times \mathbf {w} )=(\mathbf {w} \times \mathbf {u} )\cdot \mathbf {v} =\det(\mathbf {u} \mathbf {v} \mathbf {w} ).$

To prove this diagrammatically, note that all of the following figures are different depictions of the same 3-trace diagram (as specified by the above definition):

Combining the above diagrams for the cross product and the dot product, one can read off the three leftmost diagrams as precisely the three leftmost scalar triple products in the above identity. It can also be shown that the rightmost diagram represents det[uvw]. The scalar triple product identity follows because each is a different representation of the same diagram's function.

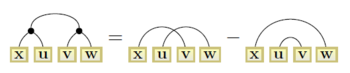
As a second example, one can show that

(where the equality indicates that the identity holds for the underlying multilinear functions). One can show that this kind of identity does not change by "bending" the diagram or attaching more diagrams, provided the changes are consistent across all diagrams in the identity. Thus, one can bend the top of the diagram down to the bottom, and attach vectors to each of the free edges, to obtain

which reads

$(\mathbf {x} \times \mathbf {u} )\cdot (\mathbf {v} \times \mathbf {w} )=(\mathbf {x} \cdot \mathbf {v} )(\mathbf {u} \cdot \mathbf {w} )-(\mathbf {x} \cdot \mathbf {w} )(\mathbf {u} \cdot \mathbf {v} ),$

a well-known identity relating four 3-dimensional vectors.

Diagrams with matrices

The simplest closed diagrams with a single matrix label correspond to the coefficients of thecharacteristic polynomial,up to a scalar factor that depends only on the dimension of the matrix. One representation of these diagrams is shown below, where$\propto$is used to indicate equality up to a scalar factor that depends only on the dimensionnof the underlying vector space.

.

Properties

LetGbe the group of n×n matrices. If a closed trace diagram is labeled bykdifferent matrices, it may be interpreted as a function from$G^{k}$to an algebra of multilinear functions. This function isinvariantunder simultaneousconjugation,that is, the function corresponding to$(g_{1},\ldots,g_{k})$is the same as the function corresponding to$(ag_{1}a^{-1},\ldots,ag_{k}a^{-1})$for any invertible$a\in G$.

Extensions and applications

Trace diagrams may be specialized for particularLie groupsby altering the definition slightly. In this context, they are sometimes calledbirdtracks,tensor diagrams,orPenrose graphical notation.

Trace diagrams have primarily been used by physicists as a tool for studyingLie groups.The most common applications userepresentation theoryto constructspin networksfrom trace diagrams. In mathematics, they have been used to studycharacter varieties.

See also

• Multilinear map
• Gain graph

References

Books:

• Diagram Techniques in Group Theory,G. E. Stedman, Cambridge University Press, 1990
• Group Theory: Birdtracks, Lie's, and Exceptional Groups,Predrag Cvitanović,Princeton University Press, 2008,http://birdtracks.eu/