Young tableau

Inmathematics,aYoung tableau(/tæˈbloʊ,ˈtæbloʊ/;plural:tableaux) is acombinatorialobject useful inrepresentation theoryandSchubert calculus.It provides a convenient way to describe thegroup representationsof thesymmetricandgeneral lineargroups and to study their properties. Young tableaux were introduced byAlfred Young,amathematicianatCambridge University,in 1900.^[1]^[2]They were then applied to the study of the symmetric group byGeorg Frobeniusin 1903. Their theory was further developed by many mathematicians, includingPercy MacMahon,W. V. D. Hodge,G. de B. Robinson,Gian-Carlo Rota,Alain Lascoux,Marcel-Paul SchützenbergerandRichard P. Stanley.

Definitions

Note: this article uses the English convention for displaying Young diagrams and tableaux.

Diagrams

AYoung diagram(also called aFerrers diagram,particularly when represented using dots) is a finite collection of boxes, or cells, arranged in left-justified rows, with the row lengths in non-increasing order. Listing the number of boxes in each row gives apartition $λ$ of a non-negative integer $n$ ,the total number of boxes of the diagram. The Young diagram is said to be of shape $λ$ ,and it carries the same information as that partition. Containment of one Young diagram in another defines apartial orderingon the set of all partitions, which is in fact alatticestructure, known asYoung's lattice.Listing the number of boxes of a Young diagram in each column gives another partition, theconjugateortransposepartition of $λ$ ;one obtains a Young diagram of that shape by reflecting the original diagram along its main diagonal.

There is almost universal agreement that in labeling boxes of Young diagrams by pairs of integers, the first index selects the row of the diagram, and the second index selects the box within the row. Nevertheless, two distinct conventions exist to display these diagrams, and consequently tableaux: the first places each row below the previous one, the second stacks each row on top of the previous one. Since the former convention is mainly used byAnglophoneswhile the latter is often preferred byFrancophones,it is customary to refer to these conventions respectively as theEnglish notationand theFrench notation;for instance, in his book onsymmetric functions,Macdonaldadvises readers preferring the French convention to "read this book upside down in a mirror" (Macdonald 1979, p. 2). This nomenclature probably started out as jocular. The English notation corresponds to the one universally used for matrices, while the French notation is closer to the convention ofCartesian coordinates;however, French notation differs from that convention by placing the vertical coordinate first. The figure on the right shows, using the English notation, the Young diagram corresponding to the partition (5, 4, 1) of the number 10. The conjugate partition, measuring the column lengths, is (3, 2, 2, 2, 1).

Arm and leg length

In many applications, for example when definingJack functions,it is convenient to define thearm lengtha_λ(s) of a boxsas the number of boxes to the right ofsin the diagram λ in English notation. Similarly, theleg lengthl_λ(s) is the number of boxes belows.Thehook lengthof a boxsis the number of boxes to the right ofsor belowsin English notation, including the boxsitself; in other words, the hook length isa_λ(s) +l_λ(s) + 1.

Tableaux

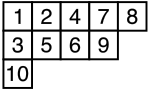
AYoung tableauis obtained by filling in the boxes of the Young diagram with symbols taken from somealphabet,which is usually required to be atotally ordered set.Originally that alphabet was a set of indexed variables $x 1$ , $x 2$ , $x 3$ ..., but now one usually uses a set of numbers for brevity. In their original application torepresentations of the symmetric group,Young tableaux have $n$ distinct entries, arbitrarily assigned to boxes of the diagram. A tableau is calledstandardif the entries in each row and each column are increasing. The number of distinct standard Young tableaux on $n$ entries is given by theinvolution numbers

1, 1, 2, 4, 10, 26, 76, 232, 764, 2620, 9496,... (sequenceA000085in theOEIS).

In other applications, it is natural to allow the same number to appear more than once (or not at all) in a tableau. A tableau is calledsemistandard,orcolumn strict,if the entries weakly increase along each row and strictly increase down each column. Recording the number of times each number appears in a tableau gives a sequence known as theweightof the tableau. Thus the standard Young tableaux are precisely the semistandard tableaux of weight (1,1,...,1), which requires every integer up to $n$ to occur exactly once.

In a standard Young tableau, the integer $k$ is adescentif $k+1$ appears in a row strictly below $k$ .The sum of the descents is called themajor indexof the tableau.^[3]

Variations

There are several variations of this definition: for example, in a row-strict tableau the entries strictly increase along the rows and weakly increase down the columns. Also, tableaux withdecreasingentries have been considered, notably, in the theory ofplane partitions.There are also generalizations such as domino tableaux or ribbon tableaux, in which several boxes may be grouped together before assigning entries to them.

Skew tableaux

Askew shapeis a pair of partitions ( $λ$ , $μ$ ) such that the Young diagram of $λ$ contains the Young diagram of $μ$ ;it is denoted by $λ / μ$ .If $λ = (λ 1, λ 2,...)$ and $μ = (μ 1, μ 2,...)$ ,then the containment of diagrams means that $μ i \leq λ i$ for all $i$ .Theskew diagramof a skew shape $λ / μ$ is the set-theoretic difference of the Young diagrams of $λ$ and $μ$ :the set of squares that belong to the diagram of $λ$ but not to that of $μ$ .Askew tableauof shape $λ / μ$ is obtained by filling the squares of the corresponding skew diagram; such a tableau is semistandard if entries increase weakly along each row, and increase strictly down each column, and it is standard if moreover all numbers from 1 to the number of squares of the skew diagram occur exactly once. While the map from partitions to their Young diagrams is injective, this is not the case for the map from skew shapes to skew diagrams;^[4]therefore the shape of a skew diagram cannot always be determined from the set of filled squares only. Although many properties of skew tableaux only depend on the filled squares, some operations defined on them do require explicit knowledge of $λ$ and $μ$ ,so it is important that skew tableaux do record this information: two distinct skew tableaux may differ only in their shape, while they occupy the same set of squares, each filled with the same entries.^[5]Young tableaux can be identified with skew tableaux in which $μ$ is the empty partition (0) (the unique partition of 0).

Any skew semistandard tableau $T$ of shape $λ / μ$ with positive integer entries gives rise to a sequence of partitions (or Young diagrams), by starting with $μ$ ,and taking for the partition $i$ places further in the sequence the one whose diagram is obtained from that of $μ$ by adding all the boxes that contain a value ≤ $i$ in $T$ ;this partition eventually becomes equal to $λ$ .Any pair of successive shapes in such a sequence is a skew shape whose diagram contains at most one box in each column; such shapes are calledhorizontal strips.This sequence of partitions completely determines $T$ ,and it is in fact possible to define (skew) semistandard tableaux as such sequences, as is done by Macdonald (Macdonald 1979, p. 4). This definition incorporates the partitions $λ$ and $μ$ in the data comprising the skew tableau.

Overview of applications

Young tableaux have numerous applications incombinatorics,representation theory,andalgebraic geometry.Various ways of counting Young tableaux have been explored and lead to the definition of and identities forSchur functions.

Many combinatorial algorithms on tableaux are known, including Schützenberger'sjeu de taquinand theRobinson–Schensted–Knuth correspondence.Lascoux and Schützenberger studied anassociativeproduct on the set of all semistandard Young tableaux, giving it the structure called theplactic monoid(French:le monoïde plaxique).

In representation theory, standard Young tableaux of size $k$ describe bases in irreducible representations of thesymmetric groupon $k$ letters. Thestandard monomial basisin a finite-dimensionalirreducible representationof thegeneral linear group $GL n$ are parametrized by the set of semistandard Young tableaux of a fixed shape over the alphabet {1, 2,..., $n$ }. This has important consequences forinvariant theory,starting from the work ofHodgeon thehomogeneous coordinate ringof theGrassmannianand further explored byGian-Carlo Rotawith collaborators,de ConciniandProcesi,andEisenbud.TheLittlewood–Richardson ruledescribing (among other things) the decomposition oftensor productsof irreducible representations of $GL n$ into irreducible components is formulated in terms of certain skew semistandard tableaux.

Applications to algebraic geometry center aroundSchubert calculuson Grassmannians andflag varieties.Certain importantcohomology classescan be represented bySchubert polynomialsand described in terms of Young tableaux.

Applications in representation theory

Young diagrams are in one-to-one correspondence withirreducible representationsof thesymmetric groupover thecomplex numbers.They provide a convenient way of specifying theYoung symmetrizersfrom which theirreducible representationsare built. Many facts about a representation can be deduced from the corresponding diagram. Below, we describe two examples: determining the dimension of a representation and restricted representations. In both cases, we will see that some properties of a representation can be determined by using just its diagram. Young tableaux are involved in the use of the symmetric group in quantum chemistry studies of atoms, molecules and solids.^[6]^[7]

Young diagrams also parametrize the irreducible polynomial representations of thegeneral linear group $GL n$ (when they have at most $n$ nonempty rows), or the irreducible representations of thespecial linear group $SL n$ (when they have at most $n - 1$ nonempty rows), or the irreducible complex representations of thespecial unitary group $SU n$ (again when they have at most $n - 1$ nonempty rows). In these cases semistandard tableaux with entries up to $n$ play a central role, rather than standard tableaux; in particular it is the number of those tableaux that determines the dimension of the representation.

Dimension of a representation

Hook-lengthsof the boxes for the partition 10 = 5 + 4 + 1

The dimension of the irreducible representation $π λ$ of the symmetric group $S n$ corresponding to a partition $λ$ of $n$ is equal to the number of different standard Young tableaux that can be obtained from the diagram of the representation. This number can be calculated by thehook length formula.

Ahook length $hook(x)$ of a box $x$ in Young diagram $Y (λ)$ of shape $λ$ is the number of boxes that are in the same row to the right of it plus those boxes in the same column below it, plus one (for the box itself). By the hook-length formula, the dimension of an irreducible representation is $n!$ divided by the product of the hook lengths of all boxes in the diagram of the representation:

\dim \pi _{\lambda }={\frac {n!}{\prod _{x\in Y(\lambda )}\operatorname {hook} (x)}}.

The figure on the right shows hook-lengths for all boxes in the diagram of the partition 10 = 5 + 4 + 1. Thus

\dim \pi _{\lambda }={\frac {10!}{7\cdot 5\cdot 4\cdot 3\cdot 1\cdot 5\cdot 3\cdot 2\cdot 1\cdot 1}}=288.

Similarly, the dimension of the irreducible representation $W (λ)$ of $GL r$ corresponding to the partitionλofn(with at mostrparts) is the number of semistandard Young tableaux of shapeλ(containing only the entries from 1 tor), which is given by the hook-length formula:

\dim W(\lambda )=\prod _{(i,j)\in Y(\lambda )}{\frac {r+j-i}{\operatorname {hook} (i,j)}},

where the indexigives the row andjthe column of a box.^[8]For instance, for the partition (5,4,1) we get as dimension of the corresponding irreducible representation of $GL 7$ (traversing the boxes by rows):

\dim W(\lambda )={\frac {7\cdot 8\cdot 9\cdot 10\cdot 11\cdot 6\cdot 7\cdot 8\cdot 9\cdot 5}{7\cdot 5\cdot 4\cdot 3\cdot 1\cdot 5\cdot 3\cdot 2\cdot 1\cdot 1}}=66528.

Restricted representations

A representation of the symmetric group on $n$ elements, $S n$ is also a representation of the symmetric group on $n - 1$ elements, $S n -1$ .However, an irreducible representation of $S n$ may not be irreducible for $S n -1$ .Instead, it may be adirect sumof several representations that are irreducible for $S n -1$ .These representations are then called the factors of therestricted representation(see alsoinduced representation).

The question of determining this decomposition of the restricted representation of a given irreducible representation ofS_n,corresponding to a partition $λ$ of $n$ ,is answered as follows. One forms the set of all Young diagrams that can be obtained from the diagram of shape $λ$ by removing just one box (which must be at the end both of its row and of its column); the restricted representation then decomposes as a direct sum of the irreducible representations of $S n -1$ corresponding to those diagrams, each occurring exactly once in the sum.

Notes

^Knuth, Donald E.(1973),The Art of Computer Programming, Vol. III: Sorting and Searching(2nd ed.), Addison-Wesley, p. 48,Such arrangements were introduced by Alfred Young in 1900.
^Young, A. (1900),"On quantitative substitutional analysis",Proceedings of the London Mathematical Society,Series 1,33(1): 97–145,doi:10.1112/plms/s1-33.1.97.See in particular p. 133.
^Stembridge, John (1989-12-01)."On the eigenvalues of representations of reflection groups and wreath products".Pacific Journal of Mathematics.140(2). Mathematical Sciences Publishers: 353–396.doi:10.2140/pjm.1989.140.353.ISSN 0030-8730.
^For instance the skew diagram consisting of a single square at position (2,4) can be obtained by removing the diagram of $μ = (5,3,2,1)$ from the one of $λ = (5,4,2,1)$ ,but also in (infinitely) many other ways. In general any skew diagram whose set of non-empty rows (or of non-empty columns) is not contiguous or does not contain the first row (respectively column) will be associated to more than one skew shape.
^A somewhat similar situation arises for matrices: the 3-by-0 matrix $A$ must be distinguished from the 0-by-3 matrix $B$ ,since $AB$ is a 3-by-3 (zero) matrix while $BA$ is the 0-by-0 matrix, but both $A$ and $B$ have the same (empty) set of entries; for skew tableaux however such distinction is necessary even in cases where the set of entries is not empty.
^Philip R. Bunker and Per Jensen (1998)Molecular Symmetry and Spectroscopy, 2nd ed. NRC Research Press, Ottawa[1] pp.198-202.ISBN 9780660196282
^R.Pauncz (1995)The Symmetric Group in Quantum Chemistry, CRC Press, Boca Raton, Florida
^Predrag Cvitanović(2008).Group Theory: Birdtracks, Lie's, and Exceptional Groups.Princeton University Press.,eq. 9.28 and appendix B.4

References

William Fulton.Young Tableaux, with Applications to Representation Theory and Geometry.Cambridge University Press, 1997,ISBN 0-521-56724-6.
Fulton, William;Harris, Joe(1991).Representation theory. A first course.Graduate Texts in Mathematics,Readings in Mathematics. Vol. 129. New York: Springer-Verlag.doi:10.1007/978-1-4612-0979-9.ISBN 978-0-387-97495-8.MR 1153249.OCLC 246650103.Lecture 4
Howard Georgi, Lie Algebras in Particle Physics, 2nd Edition - Westview
Macdonald, I. G.Symmetric functions and Hall polynomials.Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, Oxford, 1979. viii+180 pp.ISBN 0-19-853530-9 MR553598
Laurent Manivel.Symmetric Functions, Schubert Polynomials, and Degeneracy Loci.American Mathematical Society.
Greene, Curtis;Nijenhuis, Albert;Wilf, Herbert S.(1979)."A probabilistic proof of a formula for the number of Young tableaux of a given shape".Advances in Mathematics.31(1). Amsterdam:Elsevier:104–109.doi:10.1016/0001-8708(79)90023-9.MR 0521470.Zbl 0398.05008.
Jean-Christophe Novelli,Igor Pak,Alexander V. Stoyanovskii, "A direct bijective proof of the Hook-length formula",Discrete Mathematics and Theoretical Computer Science1(1997), pp. 53–67.
Bruce E. Sagan.The Symmetric Group.Springer, 2001,ISBN 0-387-95067-2
Vinberg, E.B.(2001) [1994],"Young tableau",Encyclopedia of Mathematics,EMS Press
Yong, Alexander (February 2007)."What is...a Young Tableau?"(PDF).Notices of the American Mathematical Society.54(2): 240–241.Retrieved2008-01-16.
Predrag Cvitanović,Group Theory: Birdtracks, Lie's, and Exceptional Groups.Princeton University Press, 2008.

External links

Eric W. Weisstein. "Ferrers Diagram".From MathWorld—A Wolfram Web Resource.
Eric W. Weisstein. "Young Tableau."From MathWorld—A Wolfram Web Resource.
Semistandard tableauxentry in theFindStatdatabase
Standard tableauxentry in theFindStatdatabase

[1] Knuth, Donald E.(1973),The Art of Computer Programming, Vol. III: Sorting and Searching(2nd ed.), Addison-Wesley, p. 48,Such arrangements were introduced by Alfred Young in 1900.

[2] Young, A. (1900),"On quantitative substitutional analysis",Proceedings of the London Mathematical Society,Series 1,33(1): 97–145,doi:10.1112/plms/s1-33.1.97.See in particular p. 133.

[ste89-3] Stembridge, John (1989-12-01)."On the eigenvalues of representations of reflection groups and wreath products".Pacific Journal of Mathematics.140(2). Mathematical Sciences Publishers: 353–396.doi:10.2140/pjm.1989.140.353.ISSN 0030-8730.

[4] For instance the skew diagram consisting of a single square at position (2,4) can be obtained by removing the diagram of $μ = (5,3,2,1)$ from the one of $λ = (5,4,2,1)$ ,but also in (infinitely) many other ways. In general any skew diagram whose set of non-empty rows (or of non-empty columns) is not contiguous or does not contain the first row (respectively column) will be associated to more than one skew shape.

[5] A somewhat similar situation arises for matrices: the 3-by-0 matrix $A$ must be distinguished from the 0-by-3 matrix $B$ ,since $AB$ is a 3-by-3 (zero) matrix while $BA$ is the 0-by-0 matrix, but both $A$ and $B$ have the same (empty) set of entries; for skew tableaux however such distinction is necessary even in cases where the set of entries is not empty.

[6] Philip R. Bunker and Per Jensen (1998)Molecular Symmetry and Spectroscopy, 2nd ed. NRC Research Press, Ottawa[1] pp.198-202.ISBN 9780660196282

[7] R.Pauncz (1995)The Symmetric Group in Quantum Chemistry, CRC Press, Boca Raton, Florida

[8] Predrag Cvitanović(2008).Group Theory: Birdtracks, Lie's, and Exceptional Groups.Princeton University Press.,eq. 9.28 and appendix B.4

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]