Viscosity
| Viscosity | |
|---|---|
 A simulation of liquids with different viscosities. The liquid on the left has lower viscosity than the liquid on the right. | |
Common symbols | η,μ |
Derivations from other quantities | μ=G·t |
| Dimension | |
| Part of a series on |
| Continuum mechanics |
|---|
Viscosityis a measure of afluid'sdynamicresistanceto a change in shape or to movement of its neighboring portions relative to one another.[1]For liquids, it corresponds to the informal concept ofthickness;for example,syruphas a higher viscosity thanwater.[2]Viscosity is defined scientifically as a force multiplied by a time divided by an area. Thus itsSI unitsare newton-seconds per square meter, or pascal-seconds.[1]
Viscosity quantifies the internalfrictional forcebetween adjacent layers of fluid that are in relative motion.[1]For instance, when a viscous fluid is forced through a tube, it flows more quickly near the tube's center line than near its walls.[3]Experiments show that somestress(such as apressuredifference between the two ends of the tube) is needed to sustain the flow. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion. For a tube with a constant rate of flow, the strength of the compensating force is proportional to the fluid's viscosity.
In general, viscosity depends on a fluid's state, such as its temperature, pressure, and rate of deformation. However, the dependence on some of these properties is negligible in certain cases. For example, the viscosity of aNewtonian fluiddoes not vary significantly with the rate of deformation.
Zero viscosity (no resistance toshear stress) is observed only atvery low temperaturesinsuperfluids;otherwise, thesecond law of thermodynamicsrequires all fluids to have positive viscosity.[4][5]A fluid that has zero viscosity (non-viscous) is calledidealorinviscid.
Fornon-Newtonian fluid's viscosity, there arepseudoplastic,plastic,anddilatantflows that are time-independent, and there arethixotropicandrheopecticflows that are time-dependent.
Etymology
[edit]The word "viscosity" is derived from theLatinviscum( "mistletoe").Viscumalso referred to a viscousgluederived from mistletoe berries.[6]
Definitions
[edit]Dynamic viscosity
[edit]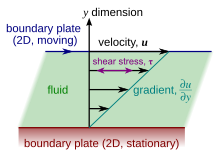

Inmaterials scienceandengineering,there is often interest in understanding the forces orstressesinvolved in thedeformationof a material. For instance, if the material were a simple spring, the answer would be given byHooke's law,which says that the force experienced by a spring is proportional to the distance displaced from equilibrium. Stresses which can be attributed to the deformation of a material from some rest state are calledelasticstresses. In other materials, stresses are present which can be attributed to thedeformation rate over time.These are called viscous stresses. For instance, in a fluid such as water the stresses which arise from shearing the fluid do not depend on thedistancethe fluid has been sheared; rather, they depend on howquicklythe shearing occurs.
Viscosity is the material property which relates the viscous stresses in a material to the rate of change of a deformation (the strain rate). Although it applies to general flows, it is easy to visualize and define in a simple shearing flow, such as a planarCouette flow.
In the Couette flow, a fluid is trapped between two infinitely large plates, one fixed and one in parallel motion at constant speed(see illustration to the right). If the speed of the top plate is low enough (to avoid turbulence), then in steady state the fluid particles move parallel to it, and their speed varies fromat the bottom toat the top.[7]Each layer of fluid moves faster than the one just below it, and friction between them gives rise to aforceresisting their relative motion. In particular, the fluid applies on the top plate a force in the direction opposite to its motion, and an equal but opposite force on the bottom plate. An external force is therefore required in order to keep the top plate moving at constant speed.
In many fluids, the flow velocity is observed to vary linearly from zero at the bottom toat the top. Moreover, the magnitude of the force,,acting on the top plate is found to be proportional to the speedand the areaof each plate, and inversely proportional to their separation:
The proportionality factor is thedynamic viscosityof the fluid, often simply referred to as theviscosity.It is denoted by theGreek letter mu(μ). The dynamic viscosity has thedimensions,therefore resulting in theSI unitsand thederived units:
The aforementioned ratiois called therate of shear deformationorshear velocity,and is thederivativeof the fluid speed in the directionparallelto the normal vector of the plates (see illustrations to the right). If the velocity does not vary linearly with,then the appropriate generalization is:
where,andis the local shear velocity. This expression is referred to asNewton's law of viscosity.In shearing flows with planar symmetry, it is whatdefines.It is a special case of the general definition of viscosity (see below), which can be expressed in coordinate-free form.
Use of theGreek letter mu() for the dynamic viscosity (sometimes also called theabsolute viscosity) is common amongmechanicalandchemical engineers,as well as mathematicians and physicists.[8][9][10]However, theGreek letter eta() is also used by chemists, physicists, and theIUPAC.[11]The viscosityis sometimes also called theshear viscosity.However, at least one author discourages the use of this terminology, noting thatcan appear in non-shearing flows in addition to shearing flows.[12]
Kinematic viscosity
[edit]In fluid dynamics, it is sometimes more appropriate to work in terms ofkinematic viscosity(sometimes also called themomentum diffusivity), defined as the ratio of the dynamic viscosity (μ) over thedensityof the fluid (ρ). It is usually denoted by theGreek letter nu(ν):
and has thedimensions,therefore resulting in theSI unitsand thederived units:
- specific energymultiplied bytimeenergy per unit mass multiplied by time.
General definition
[edit]In very general terms, the viscous stresses in a fluid are defined as those resulting from the relative velocity of different fluid particles. As such, the viscous stresses must depend on spatial gradients of the flow velocity. If the velocity gradients are small, then to a first approximation the viscous stresses depend only on the first derivatives of the velocity.[13](For Newtonian fluids, this is also a linear dependence.) In Cartesian coordinates, the general relationship can then be written as
whereis a viscosity tensor that maps thevelocity gradienttensoronto the viscous stress tensor.[14]Since the indices in this expression can vary from 1 to 3, there are 81 "viscosity coefficients"in total. However, assuming that the viscosity rank-2 tensor isisotropicreduces these 81 coefficients to three independent parameters,,:
and furthermore, it is assumed that no viscous forces may arise when the fluid is undergoing simple rigid-body rotation, thus,leaving only two independent parameters.[13]The most usual decomposition is in terms of the standard (scalar) viscosityand thebulk viscositysuch thatand.In vector notation this appears as:
whereis the unit tensor.[12][15]This equation can be thought of as a generalized form of Newton's law of viscosity.
The bulk viscosity (also called volume viscosity) expresses a type of internal friction that resists the shearless compression or expansion of a fluid. Knowledge ofis frequently not necessary in fluid dynamics problems. For example, an incompressible fluid satisfiesand so the term containingdrops out. Moreover,is often assumed to be negligible for gases since it isin amonatomicideal gas.[12]One situation in whichcan be important is the calculation of energy loss insoundandshock waves,described byStokes' law of sound attenuation,since these phenomena involve rapid expansions and compressions.
The defining equations for viscosity are not fundamental laws of nature, so their usefulness, as well as methods for measuring or calculating the viscosity, must be established using separate means. A potential issue is that viscosity depends, in principle, on the full microscopic state of the fluid, which encompasses the positions and momenta of every particle in the system.[16]Such highly detailed information is typically not available in realistic systems. However, under certain conditions most of this information can be shown to be negligible. In particular, for Newtonian fluids near equilibrium and far from boundaries (bulk state), the viscosity depends only space- and time-dependent macroscopic fields (such as temperature and density) defining local equilibrium.[16][17]
Nevertheless, viscosity may still carry a non-negligible dependence on several system properties, such as temperature, pressure, and the amplitude and frequency of any external forcing. Therefore, precision measurements of viscosity are only defined with respect to a specific fluid state.[18]To standardize comparisons among experiments and theoretical models, viscosity data is sometimes extrapolated to ideal limiting cases, such as thezero shearlimit, or (for gases) thezero densitylimit.
Momentum transport
[edit]Transport theory provides an alternative interpretation of viscosity in terms of momentum transport: viscosity is the material property which characterizes momentum transport within a fluid, just asthermal conductivitycharacterizesheattransport, and (mass)diffusivitycharacterizes mass transport.[19]This perspective is implicit in Newton's law of viscosity,,because the shear stresshas units equivalent to a momentumflux,i.e., momentum per unit time per unit area. Thus,can be interpreted as specifying the flow of momentum in thedirection from one fluid layer to the next. Per Newton's law of viscosity, this momentum flow occurs across a velocity gradient, and the magnitude of the corresponding momentum flux is determined by the viscosity.
The analogy with heat and mass transfer can be made explicit. Just as heat flows from high temperature to low temperature and mass flows from high density to low density, momentum flows from high velocity to low velocity. These behaviors are all described by compact expressions, calledconstitutive relations,whose one-dimensional forms are given here:
whereis the density,andare the mass and heat fluxes, andandare the mass diffusivity and thermal conductivity.[20]The fact that mass, momentum, and energy (heat) transport are among the most relevant processes in continuum mechanics is not a coincidence: these are among the few physical quantities that are conserved at the microscopic level in interparticle collisions. Thus, rather than being dictated by the fast and complex microscopic interaction timescale, their dynamics occurs on macroscopic timescales, as described by the various equations of transport theory and hydrodynamics.
Newtonian and non-Newtonian fluids
[edit]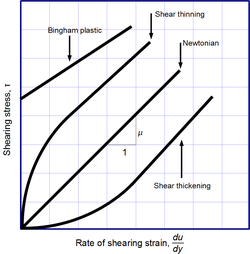
Newton's law of viscosity is not a fundamental law of nature, but rather aconstitutive equation(likeHooke's law,Fick's law,andOhm's law) which serves to define the viscosity.Its form is motivated by experiments which show that for a wide range of fluids,is independent of strain rate. Such fluids are calledNewtonian.Gases,water,and many common liquids can be considered Newtonian in ordinary conditions and contexts. However, there are manynon-Newtonian fluidsthat significantly deviate from this behavior. For example:
- Shear-thickening(dilatant) liquids, whose viscosity increases with the rate of shear strain.
- Shear-thinningliquids, whose viscosity decreases with the rate of shear strain.
- Thixotropicliquids, that become less viscous over time when shaken, agitated, or otherwise stressed.
- Rheopecticliquids, that become more viscous over time when shaken, agitated, or otherwise stressed.
- Bingham plasticsthat behave as a solid at low stresses but flow as a viscous fluid at high stresses.
Trouton's ratio is the ratio ofextensional viscositytoshear viscosity.For a Newtonian fluid, the Trouton ratio is 3.[21][22]Shear-thinning liquids are very commonly, but misleadingly, described as thixotropic.[23]
Viscosity may also depend on the fluid's physical state (temperature and pressure) and other,external,factors. For gases and othercompressible fluids,it depends on temperature and varies very slowly with pressure. The viscosity of some fluids may depend on other factors. Amagnetorheological fluid,for example, becomes thicker when subjected to amagnetic field,possibly to the point of behaving like a solid.
In solids
[edit]The viscous forces that arise during fluid flow are distinct from theelasticforces that occur in a solid in response to shear, compression, or extension stresses. While in the latter the stress is proportional to theamountof shear deformation, in a fluid it is proportional to therateof deformation over time. For this reason,James Clerk Maxwellused the termfugitive elasticityfor fluid viscosity.
However, many liquids (including water) will briefly react like elastic solids when subjected to sudden stress. Conversely, many "solids" (evengranite) will flow like liquids, albeit very slowly, even under arbitrarily small stress.[24]Such materials are best described asviscoelastic—that is, possessing both elasticity (reaction to deformation) and viscosity (reaction to rate of deformation).
Viscoelastic solids may exhibit both shear viscosity and bulk viscosity. Theextensional viscosityis alinear combinationof the shear and bulk viscosities that describes the reaction of a solid elastic material to elongation. It is widely used for characterizing polymers.
Ingeology,earth materials that exhibit viscous deformation at least threeorders of magnitudegreater than their elastic deformation are sometimes calledrheids.[25]
Measurement
[edit]Viscosity is measured with various types ofviscometersandrheometers.Close temperature control of the fluid is essential to obtain accurate measurements, particularly in materials like lubricants, whose viscosity can double with a change of only 5 °C. A rheometer is used for fluids that cannot be defined by a single value of viscosity and therefore require more parameters to be set and measured than is the case for a viscometer.[26]
For some fluids, the viscosity is constant over a wide range of shear rates (Newtonian fluids). The fluids without a constant viscosity (non-Newtonian fluids) cannot be described by a single number. Non-Newtonian fluids exhibit a variety of different correlations between shear stress and shear rate.
One of the most common instruments for measuring kinematic viscosity is the glass capillary viscometer.
Incoatingindustries, viscosity may be measured with a cup in which theefflux timeis measured. There are several sorts of cup—such as theZahn cupand theFord viscosity cup—with the usage of each type varying mainly according to the industry.
Also used in coatings, aStormer viscometeremploys load-based rotation to determine viscosity. The viscosity is reported in Krebs units (KU), which are unique to Stormer viscometers.
Vibrating viscometers can also be used to measure viscosity. Resonant, or vibrational viscometers work by creating shear waves within the liquid. In this method, the sensor is submerged in the fluid and is made to resonate at a specific frequency. As the surface of the sensor shears through the liquid, energy is lost due to its viscosity. This dissipated energy is then measured and converted into a viscosity reading. A higher viscosity causes a greater loss of energy.[citation needed]
Extensional viscositycan be measured with variousrheometersthat applyextensional stress.
Volume viscositycan be measured with anacoustic rheometer.
Apparent viscosityis a calculation derived from tests performed ondrilling fluidused in oil or gas well development. These calculations and tests help engineers develop and maintain the properties of the drilling fluid to the specifications required.
Nanoviscosity (viscosity sensed by nanoprobes) can be measured byfluorescence correlation spectroscopy.[27]
Units
[edit]TheSIunit of dynamic viscosity is thenewton-second per square meter (N·s/m2), also frequently expressed in the equivalent formspascal-second(Pa·s),kilogramper meter per second (kg·m−1·s−1) andpoiseuille(Pl). TheCGSunit is thepoise(P, or g·cm−1·s−1= 0.1 Pa·s),[28]named afterJean Léonard Marie Poiseuille.It is commonly expressed, particularly inASTMstandards, ascentipoise(cP). The centipoise is convenient because the viscosity of water at 20 °C is about 1 cP, and one centipoise is equal to the SI millipascal second (mPa·s).
The SI unit of kinematic viscosity is square meter per second (m2/s), whereas the CGS unit for kinematic viscosity is thestokes(St, or cm2·s−1= 0.0001 m2·s−1), named after SirGeorge Gabriel Stokes.[29]In U.S. usage,stokeis sometimes used as the singular form. Thesubmultiplecentistokes(cSt) is often used instead, 1 cSt = 1 mm2·s−1= 10−6m2·s−1.1 cSt is 1 cP divided by 1000 kg/m^3, close to the density of water. The kinematic viscosity of water at 20 °C is about 1 cSt.
The most frequently used systems ofUS customary, or Imperial,units are theBritish Gravitational(BG) andEnglish Engineering(EE). In the BG system, dynamic viscosity has units ofpound-seconds per squarefoot(lb·s/ft2), and in the EE system it has units ofpound-force-seconds per square foot (lbf·s/ft2). The pound and pound-force are equivalent; the two systems differ only in how force and mass are defined. In the BG system the pound is a basic unit from which the unit of mass (theslug) is defined byNewton's Second Law,whereas in the EE system the units of force and mass (the pound-force andpound-massrespectively) are defined independently through the Second Law using theproportionality constantgc.
Kinematic viscosity has units of square feet per second (ft2/s) in both the BG and EE systems.
Nonstandard units include thereyn(lbf·s/in2), a British unit of dynamic viscosity.[30]In the automotive industry theviscosity indexis used to describe the change of viscosity with temperature.
Thereciprocalof viscosity isfluidity,usually symbolized byor,depending on the convention used, measured inreciprocal poise(P−1,orcm·s·g−1), sometimes called therhe.Fluidity is seldom used inengineeringpractice.[citation needed]
At one time the petroleum industry relied on measuring kinematic viscosity by means of theSaybolt viscometer,and expressing kinematic viscosity in units ofSaybolt universal seconds(SUS).[31]Other abbreviations such as SSU (Saybolt seconds universal) or SUV (Saybolt universal viscosity) are sometimes used. Kinematic viscosity in centistokes can be converted from SUS according to the arithmetic and the reference table provided inASTMD 2161.
Molecular origins
[edit]Momentum transport in gases is mediated by discrete molecular collisions, and in liquids by attractive forces that bind molecules close together.[19]Because of this, the dynamic viscosities of liquids are typically much larger than those of gases. In addition, viscosity tends to increase with temperature in gases and decrease with temperature in liquids.
Above the liquid-gascritical point,the liquid and gas phases are replaced by a singlesupercritical phase.In this regime, the mechanisms of momentum transport interpolate between liquid-like and gas-like behavior. For example, along a supercriticalisobar(constant-pressure surface), the kinematic viscosity decreases at low temperature and increases at high temperature, with a minimum in between.[32][33]A rough estimate for the value at the minimum is
whereis thePlanck constant,is theelectron mass,andis the molecular mass.[33]
In general, however, the viscosity of a system depends in detail on how the molecules constituting the system interact, and there are no simple but correct formulas for it. The simplest exact expressions are theGreen–Kubo relationsfor the linear shear viscosity or thetransient time correlation functionexpressions derived by Evans and Morriss in 1988.[34]Although these expressions are each exact, calculating the viscosity of a dense fluid using these relations currently requires the use ofmolecular dynamicscomputer simulations. Somewhat more progress can be made for a dilute gas, as elementary assumptions about how gas molecules move and interact lead to a basic understanding of the molecular origins of viscosity. More sophisticated treatments can be constructed by systematically coarse-graining theequations of motionof the gas molecules. An example of such a treatment isChapman–Enskog theory,which derives expressions for the viscosity of a dilute gas from theBoltzmann equation.[17]
Pure gases
[edit]Elementary calculation of viscosity for a dilute gas Consider a dilute gas moving parallel to the-axis with velocitythat depends only on thecoordinate. To simplify the discussion, the gas is assumed to have uniform temperature and density.
Under these assumptions, thevelocity of a molecule passing throughis equal to whatever velocity that molecule had when its mean free pathbegan. Becauseis typically small compared with macroscopic scales, the averagevelocity of such a molecule has the form
whereis a numerical constant on the order of.(Some authors estimate;[19][35]on the other hand, a more careful calculation for rigid elastic spheres gives.) Next, because half the molecules on either side are moving towards,and doing so on average with half theaverage molecular speed,the momentum flux from either side is
The net momentum flux atis the difference of the two:
According to the definition of viscosity, this momentum flux should be equal to,which leads to
Viscosity in gases arises principally from themolecular diffusionthat transports momentum between layers of flow. An elementary calculation for a dilute gas at temperatureand densitygives
whereis theBoltzmann constant,the molecular mass, anda numerical constant on the order of.The quantity,themean free path,measures the average distance a molecule travels between collisions. Even withouta prioriknowledge of,this expression has nontrivial implications. In particular, sinceis typically inversely proportional to density and increases with temperature,itself should increase with temperature and be independent of density at fixed temperature. In fact, both of these predictions persist in more sophisticated treatments, and accurately describe experimental observations. By contrast, liquid viscosity typically decreases with temperature.[19][35]
For rigid elastic spheres of diameter,can be computed, giving
In this caseis independent of temperature, so.For more complicated molecular models, however,depends on temperature in a non-trivial way, and simple kinetic arguments as used here are inadequate. More fundamentally, the notion of a mean free path becomes imprecise for particles that interact over a finite range, which limits the usefulness of the concept for describing real-world gases.[36]
Chapman–Enskog theory
[edit]A technique developed bySydney ChapmanandDavid Enskogin the early 1900s allows a more refined calculation of.[17]It is based on theBoltzmann equation,which provides a statistical description of a dilute gas in terms of intermolecular interactions.[37]The technique allows accurate calculation offor molecular models that are more realistic than rigid elastic spheres, such as those incorporating intermolecular attractions. Doing so is necessary to reproduce the correct temperature dependence of,which experiments show increases more rapidly than thetrend predicted for rigid elastic spheres.[19]Indeed, the Chapman–Enskog analysis shows that the predicted temperature dependence can be tuned by varying the parameters in various molecular models. A simple example is the Sutherland model,[a]which describes rigid elastic spheres withweakmutual attraction. In such a case, the attractive force can be treatedperturbatively,which leads to a simple expression for:
whereis independent of temperature, being determined only by the parameters of the intermolecular attraction. To connect with experiment, it is convenient to rewrite as
whereis the viscosity at temperature.This expression is usually named Sutherland's formula.[38]Ifis known from experiments atand at least one other temperature, thencan be calculated. Expressions forobtained in this way are qualitatively accurate for a number of simple gases. Slightly more sophisticated models, such as theLennard-Jones potential,or the more flexibleMie potential,may provide better agreement with experiments, but only at the cost of a more opaque dependence on temperature. A further advantage of these more complex interaction potentials is that they can be used to develop accurate models for a wide variety of properties using the same potential parameters. In situations where little experimental data is available, this makes it possible to obtain model parameters from fitting to properties such as pure-fluidvapour-liquid equilibria,before using the parameters thus obtained to predict the viscosities of interest with reasonable accuracy.
In some systems, the assumption ofspherical symmetrymust be abandoned, as is the case for vapors with highlypolar moleculeslikeH2O.In these cases, the Chapman–Enskog analysis is significantly more complicated.[39][40]
Bulk viscosity
[edit]In the kinetic-molecular picture, a non-zero bulk viscosity arises in gases whenever there are non-negligible relaxational timescales governing the exchange of energy between the translational energy of molecules and their internal energy, e.g.rotationalandvibrational.As such, the bulk viscosity isfor a monatomic ideal gas, in which the internal energy of molecules is negligible, but is nonzero for a gas likecarbon dioxide,whose molecules possess both rotational and vibrational energy.[41][42]
Pure liquids
[edit]In contrast with gases, there is no simple yet accurate picture for the molecular origins of viscosity in liquids.
At the simplest level of description, the relative motion of adjacent layers in a liquid is opposed primarily by attractive molecular forces acting across the layer boundary. In this picture, one (correctly) expects viscosity to decrease with increasing temperature. This is because increasing temperature increases the random thermal motion of the molecules, which makes it easier for them to overcome their attractive interactions.[43]
Building on this visualization, a simple theory can be constructed in analogy with the discrete structure of a solid: groups of molecules in a liquid are visualized as forming "cages" which surround and enclose single molecules.[44]These cages can be occupied or unoccupied, and stronger molecular attraction corresponds to stronger cages. Due to random thermal motion, a molecule "hops" between cages at a rate which varies inversely with the strength of molecular attractions. Inequilibriumthese "hops" are not biased in any direction. On the other hand, in order for two adjacent layers to move relative to each other, the "hops" must be biased in the direction of the relative motion. The force required to sustain this directed motion can be estimated for a given shear rate, leading to
| (1) |
whereis theAvogadro constant,is thePlanck constant,is the volume of amoleof liquid, andis thenormal boiling point.This result has the same form as the well-known empirical relation
| (2) |
whereandare constants fit from data.[44][45]On the other hand, several authors express caution with respect to this model. Errors as large as 30% can be encountered using equation (1), compared with fitting equation (2) to experimental data.[44]More fundamentally, the physical assumptions underlying equation (1) have been criticized.[46]It has also been argued that the exponential dependence in equation (1) does not necessarily describe experimental observations more accurately than simpler, non-exponential expressions.[47][48]
In light of these shortcomings, the development of a less ad hoc model is a matter of practical interest. Foregoing simplicity in favor of precision, it is possible to write rigorous expressions for viscosity starting from the fundamental equations of motion for molecules. A classic example of this approach is Irving–Kirkwood theory.[49]On the other hand, such expressions are given as averages over multiparticlecorrelation functionsand are therefore difficult to apply in practice.
In general, empirically derived expressions (based on existing viscosity measurements) appear to be the only consistently reliable means of calculating viscosity in liquids.[50]
Local atomic structure changes observed in undercooled liquids on cooling below the equilibrium melting temperature either in terms of radial distribution functiong(r)[51]or structure factorS(Q)[52]are found to be directly responsible for the liquid fragility: deviation of the temperature dependence of viscosity of the undercooled liquid from the Arrhenius equation (2) through modification of the activation energy for viscous flow. At the same time equilibrium liquids follow the Arrhenius equation.
Mixtures and blends
[edit]Gaseous mixtures
[edit]The same molecular-kinetic picture of a single component gas can also be applied to a gaseous mixture. For instance, in theChapman–Enskogapproach the viscosityof a binary mixture of gases can be written in terms of the individual component viscosities,their respective volume fractions, and the intermolecular interactions.[17]
As for the single-component gas, the dependence ofon the parameters of the intermolecular interactions enters through various collisional integrals which may not be expressible inclosed form.To obtain usable expressions forwhich reasonably match experimental data, the collisional integrals may be computed numerically or from correlations.[53]In some cases, the collision integrals are regarded as fitting parameters, and are fitted directly to experimental data.[54]This is a common approach in the development ofreference equationsfor gas-phase viscosities. An example of such a procedure is the Sutherland approach for the single-component gas, discussed above.
For gas mixtures consisting of simple molecules,Revised Enskog Theoryhas been shown to accurately represent both the density- and temperature dependence of the viscosity over a wide range of conditions.[55][53]
Blends of liquids
[edit]As for pure liquids, the viscosity of a blend of liquids is difficult to predict from molecular principles. One method is to extend the molecular "cage" theory presented above for a pure liquid. This can be done with varying levels of sophistication. One expression resulting from such an analysis is the Lederer–Roegiers equation for a binary mixture:
whereis an empirical parameter, andandare the respectivemole fractionsand viscosities of the component liquids.[56]
Since blending is an important process in the lubricating and oil industries, a variety of empirical and proprietary equations exist for predicting the viscosity of a blend.[56]
Solutions and suspensions
[edit]Aqueous solutions
[edit]Depending on thesoluteand range of concentration, an aqueouselectrolytesolution can have either a larger or smaller viscosity compared with pure water at the same temperature and pressure. For instance, a 20% saline (sodium chloride) solution has viscosity over 1.5 times that of pure water, whereas a 20%potassium iodidesolution has viscosity about 0.91 times that of pure water.
An idealized model of dilute electrolytic solutions leads to the following prediction for the viscosityof a solution:[57]
whereis the viscosity of the solvent,is the concentration, andis a positive constant which depends on both solvent and solute properties. However, this expression is only valid for very dilute solutions, havingless than 0.1 mol/L.[58]For higher concentrations, additional terms are necessary which account for higher-order molecular correlations:
whereandare fit from data. In particular, a negative value ofis able to account for the decrease in viscosity observed in some solutions. Estimated values of these constants are shown below for sodium chloride and potassium iodide at temperature 25 °C (mol =mole,L =liter).[57]
| Solute | (mol−1/2L1/2) | (mol−1L) | (mol−2L2) |
|---|---|---|---|
| Sodium chloride(NaCl) | 0.0062 | 0.0793 | 0.0080 |
| Potassium iodide(KI) | 0.0047 | −0.0755 | 0.0000 |
Suspensions
[edit]In a suspension of solid particles (e.g.micron-size spheres suspended in oil), an effective viscositycan be defined in terms of stress and strain components which are averaged over a volume large compared with the distance between the suspended particles, but small with respect to macroscopic dimensions.[59]Such suspensions generally exhibit non-Newtonian behavior. However, for dilute systems in steady flows, the behavior is Newtonian and expressions forcan be derived directly from the particle dynamics. In a very dilute system, with volume fraction,interactions between the suspended particles can be ignored. In such a case one can explicitly calculate the flow field around each particle independently, and combine the results to obtain.For spheres, this results in the Einstein's effective viscosity formula:
whereis the viscosity of the suspending liquid. The linear dependence onis a consequence of neglecting interparticle interactions. For dilute systems in general, one expectsto take the form
where the coefficientmay depend on the particle shape (e.g. spheres, rods, disks).[60]Experimental determination of the precise value ofis difficult, however: even the predictionfor spheres has not been conclusively validated, with various experiments finding values in the range.This deficiency has been attributed to difficulty in controlling experimental conditions.[61]
In denser suspensions,acquires a nonlinear dependence on,which indicates the importance of interparticle interactions. Various analytical and semi-empirical schemes exist for capturing this regime. At the most basic level, a term quadratic inis added to:
and the coefficientis fit from experimental data or approximated from the microscopic theory. However, some authors advise caution in applying such simple formulas since non-Newtonian behavior appears in dense suspensions (for spheres),[61]or in suspensions of elongated or flexible particles.[59]
There is a distinction between a suspension of solid particles, described above, and anemulsion.The latter is a suspension of tiny droplets, which themselves may exhibit internal circulation. The presence of internal circulation can decrease the observed effective viscosity, and different theoretical or semi-empirical models must be used.[62]
Amorphous materials
[edit]
In the high and low temperature limits, viscous flow inamorphous materials(e.g. inglassesand melts)[64][65][66]has theArrhenius form:
whereQis a relevantactivation energy,given in terms of molecular parameters;Tis temperature;Ris the molargas constant;andAis approximately a constant. The activation energyQtakes a different value depending on whether the high or low temperature limit is being considered: it changes from a high valueQHat low temperatures (in the glassy state) to a low valueQLat high temperatures (in the liquid state).

For intermediate temperatures,varies nontrivially with temperature and the simple Arrhenius form fails. On the other hand, the two-exponential equation
where,,,are all constants, provides a good fit to experimental data over the entire range of temperatures, while at the same time reducing to the correct Arrhenius form in the low and high temperature limits. This expression, also known as Duouglas-Doremus-Ojovan model[67],can be motivated from various theoretical models of amorphous materials at the atomic level.[65]
A two-exponential equation for the viscosity can be derived within the Dyre shoving model of supercooled liquids, where the Arrhenius energy barrier is identified with the high-frequencyshear modulustimes a characteristic shoving volume.[68][69]Upon specifying the temperature dependence of the shear modulus via thermal expansion and via the repulsive part of the intermolecular potential, another two-exponential equation is retrieved:[70]
wheredenotes the high-frequencyshear modulusof the material evaluated at a temperature equal to theglass transitiontemperature,is the so-called shoving volume, i.e. it is the characteristic volume of the group of atoms involved in the shoving event by which an atom/molecule escapes from the cage of nearest-neighbours, typically on the order of the volume occupied by few atoms. Furthermore,is thethermal expansioncoefficient of the material,is a parameter which measures the steepness of the power-law rise of the ascending flank of the first peak of theradial distribution function,and is quantitatively related to the repulsive part of theinteratomic potential.[70]Finally,denotes theBoltzmann constant.
Eddy viscosity
[edit]In the study ofturbulenceinfluids,a common practical strategy is to ignore the small-scalevortices(oreddies) in the motion and to calculate a large-scale motion with aneffectiveviscosity, called the "eddy viscosity", which characterizes the transport and dissipation ofenergyin the smaller-scale flow (seelarge eddy simulation).[71][72]In contrast to the viscosity of the fluid itself, which must be positive by thesecond law of thermodynamics,the eddy viscosity can be negative.[73][74]
Prediction
[edit]Because viscosity depends continuously on temperature and pressure, it cannot be fully characterized by a finite number of experimental measurements. Predictive formulas become necessary if experimental values are not available at the temperatures and pressures of interest. This capability is important for thermophysical simulations, in which the temperature and pressure of a fluid can vary continuously with space and time. A similar situation is encountered for mixtures of pure fluids, where the viscosity depends continuously on the concentration ratios of the constituent fluids
For the simplest fluids, such as dilute monatomic gases and their mixtures,ab initioquantum mechanicalcomputations can accurately predict viscosity in terms of fundamental atomic constants, i.e., without reference to existing viscosity measurements.[75]For the special case of dilute helium,uncertaintiesin theab initiocalculated viscosity are two order of magnitudes smaller than uncertainties in experimental values.[76]
For slightly more complex fluids and mixtures at moderate densities (i.e.sub-critical densities)Revised Enskog Theorycan be used to predict viscosities with some accuracy.[53]Revised Enskog Theory is predictive in the sense that predictions for viscosity can be obtained using parameters fitted to other, pure-fluidthermodynamic propertiesortransport properties,thus requiring noa prioriexperimental viscosity measurements.
For most fluids, high-accuracy, first-principles computations are not feasible. Rather, theoretical or empirical expressions must be fit to existing viscosity measurements. If such an expression is fit to high-fidelity data over a large range of temperatures and pressures, then it is called a "reference correlation" for that fluid. Reference correlations have been published for many pure fluids; a few examples arewater,carbon dioxide,ammonia,benzene,andxenon.[77][78][79][80][81]Many of these cover temperature and pressure ranges that encompass gas, liquid, andsupercriticalphases.
Thermophysical modeling software often relies on reference correlations for predicting viscosity at user-specified temperature and pressure. These correlations may beproprietary.Examples areREFPROP[82](proprietary) andCoolProp[83] (open-source).
Viscosity can also be computed using formulas that express it in terms of the statistics of individual particle trajectories. These formulas include theGreen–Kubo relationsfor the linear shear viscosity and thetransient time correlation functionexpressions derived by Evans and Morriss in 1988.[84][34] The advantage of these expressions is that they are formally exact and valid for general systems. The disadvantage is that they require detailed knowledge of particle trajectories, available only in computationally expensive simulations such asmolecular dynamics. An accurate model for interparticle interactions is also required, which may be difficult to obtain for complex molecules.[85]
Selected substances
[edit]
Observed values of viscosity vary over several orders of magnitude, even for common substances (see the order of magnitude table below). For instance, a 70% sucrose (sugar) solution has a viscosity over 400 times that of water, and 26,000 times that of air.[87]More dramatically,pitchhas been estimated to have a viscosity 230 billion times that of water.[86]
Water
[edit]Thedynamic viscosityofwateris about 0.89 mPa·s at room temperature (25 °C). As a function of temperature inkelvins,the viscosity can be estimated using the semi-empiricalVogel-Fulcher-Tammann equation:
whereA= 0.02939 mPa·s,B= 507.88 K, andC= 149.3 K.[88]Experimentally determined values of the viscosity are also given in the table below. The values at 20 °C are a useful reference: there, the dynamic viscosity is about 1 cP and the kinematic viscosity is about 1 cSt.
| Temperature (°C) |
Viscosity (mPa·s or cP) |
|---|---|
| 10 | 1.305 9 |
| 20 | 1.001 6 |
| 30 | 0.797 22 |
| 50 | 0.546 52 |
| 70 | 0.403 55 |
| 90 | 0.314 17 |
Air
[edit]Under standard atmospheric conditions (25 °C and pressure of 1 bar), the dynamic viscosity of air is 18.5 μPa·s, roughly 50 times smaller than the viscosity of water at the same temperature. Except at very high pressure, the viscosity of air depends mostly on the temperature. Among the many possible approximate formulas for the temperature dependence (seeTemperature dependence of viscosity), one is:[89]
which is accurate in the range −20 °C to 400 °C. For this formula to be valid, the temperature must be given inkelvins;then corresponds to the viscosity in Pa·s.

Other common substances
[edit]| Substance | Viscosity (mPa·s) | Temperature (°C) | Ref. |
|---|---|---|---|
| Benzene | 0.604 | 25 | [87] |
| Water | 1.0016 | 20 | |
| Mercury | 1.526 | 25 | |
| Whole milk | 2.12 | 20 | [90] |
| Dark beer | 2.53 | 20 | |
| Olive oil | 56.2 | 26 | [90] |
| Honey | 2,000–10,000 | 20 | [91] |
| Ketchup[b] | 5,000–20,000 | 25 | [92] |
| Peanut butter[b] | 104–106 | [93] | |
| Pitch | 2.3×1011 | 10–30 (variable) | [86] |
Order of magnitude estimates
[edit]The following table illustrates the range of viscosity values observed in common substances. Unless otherwise noted, a temperature of 25 °C and a pressure of 1 atmosphere are assumed.
The values listed are representative estimates only, as they do not account for measurement uncertainties, variability in material definitions, or non-Newtonian behavior.
| Factor (Pa·s) | Description | Examples | Values (Pa·s) | Ref. |
|---|---|---|---|---|
| 10−6 | Lower range of gaseous viscosity |
Butane | 7.49 × 10−6 | [94] |
| Hydrogen | 8.8 × 10−6 | [95] | ||
| 10−5 | Upper range of gaseous viscosity | Krypton | 2.538 × 10−5 | [96] |
| Neon | 3.175 × 10−5 | |||
| 10−4 | Lower range of liquid viscosity | Pentane | 2.24 × 10−4 | [87] |
| Gasoline | 6 × 10−4 | |||
| Water | 8.90 × 10−4 | [87] | ||
| 10−3 | Typical range for small-molecule Newtonian liquids |
Ethanol | 1.074 × 10−3 | |
| Mercury | 1.526 × 10−3 | |||
| Whole milk(20 °C) | 2.12 × 10−3 | [90] | ||
| Blood | 3 × 10−3to 6 × 10−3 | [97] | ||
| Liquidsteel(1550 °C) | 6 × 10−3 | [98] | ||
| 10−2– 100 | Oils and long-chain hydrocarbons | Linseed oil | 0.028 | |
| Oleic acid | 0.036 | [99] | ||
| Olive oil | 0.084 | [90] | ||
| SAE 10Motor oil | 0.085 to 0.14 | |||
| Castor oil | 0.1 | |||
| SAE 20Motor oil | 0.14 to 0.42 | |||
| SAE 30Motor oil | 0.42 to 0.65 | |||
| SAE 40Motor oil | 0.65 to 0.90 | |||
| Glycerine | 1.5 | |||
| Pancake syrup | 2.5 | |||
| 101– 103 | Pastes, gels, and other semisolids (generally non-Newtonian) |
Ketchup | ≈ 101 | [92] |
| Mustard | ||||
| Sour cream | ≈ 102 | |||
| Peanut butter | [93] | |||
| Lard | ≈ 103 | |||
| ≈108 | Viscoelastic polymers | Pitch | 2.3×108 | [86] |
| ≈1021 | Certain solids under a viscoelastic description |
Mantle (geology) | ≈ 1019to 1024 | [100] |
See also
[edit]- Dashpot
- Deborah number
- Dilatant
- Herschel–Bulkley fluid
- High viscosity mixer
- Hyperviscosity syndrome
- Intrinsic viscosity
- Inviscid flow
- Joback method(estimation of liquid viscosity from molecular structure)
- Kaye effect
- Microviscosity
- Morton number
- Oil pressure
- Quasi-solid
- Rheology
- Stokes flow
- Superfluid helium-4
- Viscoplasticity
- Viscosity models for mixtures
- Zahn cup
References
[edit]Footnotes
[edit]- ^The discussion which follows draws fromChapman & Cowling 1970,pp. 232–237
- ^abThese materials are highlynon-Newtonian.
Citations
[edit]- ^abc"Viscosity".Encyclopedia Britannica.26 June 2023.Retrieved4 August2023.
- ^Growing up with Science.Marshall Cavendish.2006. p. 1928.ISBN978-0-7614-7521-7.
- ^E. Dale Martin (1961).A Study of Laminar Compressible Viscous Pipe Flow Accelerated by an Axial Body Force, with Application to Magnetogasdynamics.NASA.p. 7.
- ^Balescu 1975,pp. 428–429.
- ^Landau & Lifshitz 1987.
- ^Harper, Douglas (n.d.)."viscous (adj.)".Online Etymology Dictionary.Archivedfrom the original on 1 May 2019.Retrieved19 September2019.
- ^Mewis & Wagner 2012,p. 19.
- ^Streeter, Wylie & Bedford 1998.
- ^Holman 2002.
- ^Incropera et al. 2007.
- ^Nič et al. 1997.
- ^abcBird, Stewart & Lightfoot 2007,p. 19.
- ^abLandau & Lifshitz 1987,pp. 44–45.
- ^Bird, Stewart & Lightfoot 2007,p. 18: This source uses an alternative sign convention, which has been reversed here.
- ^Landau & Lifshitz 1987,p. 45.
- ^abBalescu 1975.
- ^abcdChapman & Cowling 1970.
- ^Millat 1996.
- ^abcdeBird, Stewart & Lightfoot 2007.
- ^Schroeder 1999.
- ^Różańska et al. 2014,pp. 47–55.
- ^Trouton 1906,pp. 426–440.
- ^Mewis & Wagner 2012,pp. 228–230.
- ^Kumagai, Sasajima & Ito 1978,pp. 157–161.
- ^Scherer, Pardenek & Swiatek 1988,p. 14.
- ^Hannan 2007.
- ^Kwapiszewska et al. 2020.
- ^McNaught & Wilkinson 1997,poise.
- ^Gyllenbok 2018,p. 213.
- ^"What is the unit called a reyn?".sizes.com.Retrieved23 December2023.
- ^ASTM D2161: Standard Practice for Conversion of Kinematic Viscosity to Saybolt Universal Viscosity or to Saybolt Furol Viscosity,ASTM,2005, p. 1
- ^Trachenko & Brazhkin 2020.
- ^abTrachenko & Brazhkin 2021.
- ^abEvans & Morriss 1988.
- ^abBellac, Mortessagne & Batrouni 2004.
- ^Chapman & Cowling 1970,p. 103.
- ^Cercignani 1975.
- ^Sutherland 1893,pp. 507–531.
- ^Bird, Stewart & Lightfoot 2007,pp. 25–27.
- ^Chapman & Cowling 1970,pp. 235–237.
- ^Chapman & Cowling 1970,pp. 197, 214–216.
- ^Cramer 2012,p. 066102-2.
- ^Reid & Sherwood 1958,p. 202.
- ^abcBird, Stewart & Lightfoot 2007,pp. 29–31.
- ^Reid & Sherwood 1958,pp. 203–204.
- ^Hildebrand 1977.
- ^Hildebrand 1977,p. 37.
- ^Egelstaff 1992,p. 264.
- ^Irving & Kirkwood 1949,pp. 817–829.
- ^Reid & Sherwood 1958,pp. 206–209.
- ^Louzguine-Luzgin, D. V. (2022-10-18)."Structural Changes in Metallic Glass-Forming Liquids on Cooling and Subsequent Vitrification in Relationship with Their Properties".Materials.15(20): 7285.Bibcode:2022Mate...15.7285L.doi:10.3390/ma15207285.ISSN1996-1944.PMC9610435.PMID36295350.
- ^Kelton, K F (2017-01-18)."Kinetic and structural fragility—a correlation between structures and dynamics in metallic liquids and glasses".Journal of Physics: Condensed Matter.29(2): 023002.Bibcode:2017JPCM...29b3002K.doi:10.1088/0953-8984/29/2/023002.ISSN0953-8984.PMID27841996.
- ^abcJervell, Vegard G.; Wilhelmsen, Øivind (2023-06-08)."Revised Enskog theory for Mie fluids: Prediction of diffusion coefficients, thermal diffusion coefficients, viscosities, and thermal conductivities".The Journal of Chemical Physics.158(22).Bibcode:2023JChPh.158v4101J.doi:10.1063/5.0149865.ISSN0021-9606.PMID37290070.S2CID259119498.
- ^Lemmon, E. W.; Jacobsen, R. T. (2004-01-01)."Viscosity and Thermal Conductivity Equations for Nitrogen, Oxygen, Argon, and Air".International Journal of Thermophysics.25(1): 21–69.Bibcode:2004IJT....25...21L.doi:10.1023/B:IJOT.0000022327.04529.f3.ISSN1572-9567.S2CID119677367.
- ^López de Haro, M.; Cohen, E. G. D.; Kincaid, J. M. (1983-03-01)."The Enskog theory for multicomponent mixtures. I. Linear transport theory".The Journal of Chemical Physics.78(5): 2746–2759.Bibcode:1983JChPh..78.2746L.doi:10.1063/1.444985.ISSN0021-9606.
- ^abZhmud 2014,p. 22.
- ^abViswanath et al. 2007.
- ^Abdulagatov, Zeinalova & Azizov 2006,pp. 75–88.
- ^abBird, Stewart & Lightfoot 2007,pp. 31–33.
- ^Bird, Stewart & Lightfoot 2007,p. 32.
- ^abMueller, Llewellin & Mader 2009,pp. 1201–1228.
- ^Bird, Stewart & Lightfoot 2007,p. 33.
- ^Fluegel 2007.
- ^Doremus 2002,pp. 7619–7629.
- ^abOjovan, Travis & Hand 2007,p. 415107.
- ^Ojovan & Lee 2004,pp. 3803–3810.
- ^P. Hrma, P. Ferkl, P., A.A.Kruger. Arrhenian to non-Arrhenian crossover in glass melt viscosity. J. Non-Cryst. Solids, 619, 122556 (2023).https://doi.org/10.1016/j.jnoncrysol.2023.122556
- ^Dyre, Olsen & Christensen 1996,p. 2171.
- ^Hecksher & Dyre 2015.
- ^abKrausser, Samwer & Zaccone 2015,p. 13762.
- ^Bird, Stewart & Lightfoot 2007,p. 163.
- ^Lesieur 2012,pp. 2–.
- ^Sivashinsky & Yakhot 1985,p. 1040.
- ^Xie & Levchenko 2019,p. 045434.
- ^Sharipov & Benites 2020.
- ^Rowland, Al Ghafri & May 2020.
- ^Huber et al. 2009.
- ^Laesecke & Muzny 2017.
- ^Monogenidou, Assael & Huber 2018.
- ^Avgeri et al. 2014.
- ^Velliadou et al. 2021.
- ^"Refprop".NIST.Nist.gov. 18 April 2013.Archivedfrom the original on 2022-02-09.Retrieved2022-02-15.
- ^Bell et al. 2014.
- ^Evans & Morriss 2007.
- ^Maginn et al. 2019.
- ^abcdEdgeworth, Dalton & Parnell 1984,pp. 198–200.
- ^abcdeRumble 2018.
- ^Viswanath & Natarajan 1989,pp. 714–715.
- ^tec-science (2020-03-25)."Viscosity of liquids and gases".tec-science.Archivedfrom the original on 2020-04-19.Retrieved2020-05-07.
- ^abcdFellows 2009.
- ^Yanniotis, Skaltsi & Karaburnioti 2006,pp. 372–377.
- ^abKoocheki et al. 2009,pp. 596–602.
- ^abCiterne, Carreau & Moan 2001,pp. 86–96.
- ^Kestin, Khalifa & Wakeham 1977.
- ^Assael et al. 2018.
- ^Kestin, Ro & Wakeham 1972.
- ^Rosenson, McCormick & Uretz 1996.
- ^Zhao et al. 2021.
- ^Sagdeev et al. 2019.
- ^Walzer, Hendel & Baumgardner.
Sources
[edit]- Abdulagatov, Ilmutdin M.; Zeinalova, Adelya B.; Azizov, Nazim D. (2006). "Experimental viscosity B-coefficients of aqueous LiCl solutions".Journal of Molecular Liquids.126(1–3): 75–88.doi:10.1016/j.molliq.2005.10.006.ISSN0167-7322.
- Assael, M. J.; et al. (2018)."Reference Values and Reference Correlations for the Thermal Conductivity and Viscosity of Fluids".Journal of Physical and Chemical Reference Data.47(2): 021501.Bibcode:2018JPCRD..47b1501A.doi:10.1063/1.5036625.ISSN0047-2689.PMC6463310.PMID30996494.
- Avgeri, S.; Assael, M. J.; Huber, M. L.; Perkins, R. A. (2014). "Reference Correlation of the Viscosity of Benzene from the Triple Point to 675 K and up to 300 MPa".Journal of Physical and Chemical Reference Data.43(3). AIP Publishing: 033103.Bibcode:2014JPCRD..43c3103A.doi:10.1063/1.4892935.ISSN0047-2689.
- Balescu, Radu(1975).Equilibrium and Non-Equilibrium Statistical Mechanics.John Wiley & Sons.ISBN978-0-471-04600-4.Archivedfrom the original on 2020-03-16.Retrieved2019-09-18.
- Bell, Ian H.; Wronski, Jorrit; Quoilin, Sylvain; Lemort, Vincent (2014-01-27)."Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp".Industrial & Engineering Chemistry Research.53(6). American Chemical Society (ACS): 2498–2508.doi:10.1021/ie4033999.ISSN0888-5885.PMC3944605.PMID24623957.
- Bellac, Michael; Mortessagne, Fabrice; Batrouni, G. George (2004).Equilibrium and Non-Equilibrium Statistical Thermodynamics.Cambridge University Press.ISBN978-0-521-82143-8.
- Bird, R. Byron; Stewart, Warren E.; Lightfoot, Edwin N. (2007).Transport Phenomena(2nd ed.). John Wiley & Sons, Inc.ISBN978-0-470-11539-8.Archivedfrom the original on 2020-03-02.Retrieved2019-09-18.
- Bird, R. Bryon; Armstrong, Robert C.; Hassager, Ole (1987),Dynamics of Polymeric Liquids, Volume 1: Fluid Mechanics(2nd ed.), John Wiley & Sons
- Cercignani, Carlo(1975).Theory and Application of the Boltzmann Equation.Elsevier.ISBN978-0-444-19450-3.
- Chapman, Sydney;Cowling, T.G.(1970).The Mathematical Theory of Non-Uniform Gases(3rd ed.). Cambridge University Press.ISBN978-0-521-07577-0.
- Citerne, Guillaume P.; Carreau, Pierre J.; Moan, Michel (2001). "Rheological properties of peanut butter".Rheologica Acta.40(1): 86–96.Bibcode:2001AcRhe..40...86C.doi:10.1007/s003970000120.S2CID94555820.
- Cramer, M.S. (2012)."Numerical estimates for the bulk viscosity of ideal gases".Physics of Fluids.24(6): 066102–066102–23.Bibcode:2012PhFl...24f6102C.doi:10.1063/1.4729611.hdl:10919/47646.Archivedfrom the original on 2022-02-15.Retrieved2020-09-19.
- Doremus, R.H. (2002). "Viscosity of silica".J. Appl. Phys.92(12): 7619–7629.Bibcode:2002JAP....92.7619D.doi:10.1063/1.1515132.
- Dyre, J.C.; Olsen, N. B.; Christensen, T. (1996)."Local elastic expansion model for viscous-flow activation energies of glass-forming molecular liquids".Physical Review B.53(5): 2171–2174.Bibcode:1996PhRvB..53.2171D.doi:10.1103/PhysRevB.53.2171.PMID9983702.S2CID39833708.
- Edgeworth, R.; Dalton, B.J.; Parnell, T. (1984)."The pitch drop experiment".European Journal of Physics.5(4): 198–200.Bibcode:1984EJPh....5..198E.doi:10.1088/0143-0807/5/4/003.S2CID250769509.Archivedfrom the original on 2013-03-28.Retrieved2009-03-31.
- Egelstaff, P. A. (1992).An Introduction to the Liquid State(2nd ed.). Oxford University Press.ISBN978-0-19-851012-3.
- Evans, Denis J.;Morriss, Gary P. (2007).Statistical Mechanics of Nonequilibrium Liquids.ANU Press.ISBN978-1-921313-22-6.JSTORj.ctt24h99q.Archivedfrom the original on 2022-01-10.Retrieved2022-01-10.
- Evans, Denis J.; Morriss, Gary P. (October 15, 1988). "Transient-time-correlation functions and the rheology of fluids".Physical Review A.38(8): 4142–4148.Bibcode:1988PhRvA..38.4142E.doi:10.1103/PhysRevA.38.4142.PMID9900865.
- Fellows, P. J. (2009).Food Processing Technology: Principles and Practice(3rd ed.). Woodhead.ISBN978-1-84569-216-2.
- Fluegel, Alexander (2007)."Viscosity calculation of glasses".Glassproperties.com.Archivedfrom the original on 2010-11-27.Retrieved2010-09-14.
- Gibbs, Philip (January 1997)."Is glass liquid or solid?".math.ucr.edu.Archivedfrom the original on 29 March 2007.Retrieved19 September2019.
- Gyllenbok, Jan(2018). "Encyclopaedia of Historical Metrology, Weights, and Measures: Volume 1".Encyclopaedia of Historical Metrology, Weights, and Measures.Vol. 1. Birkhäuser.ISBN978-3-319-57598-8.
- Hannan, Henry (2007).Technician's Formulation Handbook for Industrial and Household Cleaning Products.Waukesha, Wisconsin: Kyral LLC. p. 7.ISBN978-0-615-15601-9.
- Hecksher, Tina; Dyre, Jeppe C. (2015-01-01)."A review of experiments testing the shoving model".Journal of Non-Crystalline Solids.7th IDMRCS: Relaxation in Complex Systems.407:14–22.Bibcode:2015JNCS..407...14H.doi:10.1016/j.jnoncrysol.2014.08.056.ISSN0022-3093.Archivedfrom the original on 2022-02-15.Retrieved2021-10-17.
- Hildebrand, Joel Henry(1977).Viscosity and Diffusivity: A Predictive Treatment.John Wiley & Sons.ISBN978-0-471-03072-0.
- Holman, Jack Philip (2002).Heat Transfer.McGraw-Hill.ISBN978-0-07-112230-6.Archivedfrom the original on 2020-03-15.Retrieved2019-09-18.
- Huber, M. L.; Perkins, R. A.; Laesecke, A.; Friend, D. G.; Sengers, J. V.; Assael, M. J.; Metaxa, I. N.; Vogel, E.; Mareš, R.; Miyagawa, K. (2009). "New International Formulation for the Viscosity of H2O".Journal of Physical and Chemical Reference Data.38(2). AIP Publishing: 101–125.Bibcode:2009JPCRD..38..101H.doi:10.1063/1.3088050.ISSN0047-2689.
- Incropera, Frank P.; et al. (2007).Fundamentals of Heat and Mass Transfer.Wiley.ISBN978-0-471-45728-2.Archivedfrom the original on 2020-03-11.Retrieved2019-09-18.
- Irving, J.H.;Kirkwood, John G.(1949). "The Statistical Mechanical Theory of Transport Processes. IV. The Equations of Hydrodynamics".J. Chem. Phys.18(6): 817–829.doi:10.1063/1.1747782.
- Kestin, J.; Ro, S. T.; Wakeham, W. A. (1972)."Viscosity of the Noble Gases in the Temperature Range 25–700 °C".The Journal of Chemical Physics.56(8): 4119–4124.Bibcode:1972JChPh..56.4119K.doi:10.1063/1.1677824.ISSN0021-9606.
- Kestin, J.; Khalifa, H.E.; Wakeham, W.A. (1977). "The viscosity of five gaseous hydrocarbons".The Journal of Chemical Physics.66(3): 1132.Bibcode:1977JChPh..66.1132K.doi:10.1063/1.434048.
- Koocheki, Arash; et al. (2009). "The rheological properties of ketchup as a function of different hydrocolloids and temperature".International Journal of Food Science & Technology.44(3): 596–602.doi:10.1111/j.1365-2621.2008.01868.x.
- Krausser, J.; Samwer, K.; Zaccone, A. (2015)."Interatomic repulsion softness directly controls the fragility of supercooled metallic melts".Proceedings of the National Academy of Sciences of the USA.112(45): 13762–13767.arXiv:1510.08117.Bibcode:2015PNAS..11213762K.doi:10.1073/pnas.1503741112.PMC4653154.PMID26504208.
- Kumagai, Naoichi; Sasajima, Sadao; Ito, Hidebumi (15 February 1978)."Long-term Creep of Rocks: Results with Large Specimens Obtained in about 20 Years and Those with Small Specimens in about 3 Years".Journal of the Society of Materials Science (Japan).27(293): 157–161.NAID110002299397.Archivedfrom the original on 2011-05-21.Retrieved2008-06-16.
- Kwapiszewska, Karina; Szczepański, Krzysztof; Kalwarczyk, Tomasz; Michalska, Bernadeta; Patalas-Krawczyk, Paulina; Szymański, Jędrzej; Andryszewski, Tomasz; Iwan, Michalina; Duszyński, Jerzy; Hołyst, Robert (2020)."Nanoscale Viscosity of Cytoplasm Is Conserved in Human Cell Lines".The Journal of Physical Chemistry Letters.11(16): 6914–6920.doi:10.1021/acs.jpclett.0c01748.PMC7450658.PMID32787203.
- Laesecke, Arno; Muzny, Chris D. (2017)."Reference Correlation for the Viscosity of Carbon Dioxide".Journal of Physical and Chemical Reference Data.46(1). AIP Publishing: 013107.Bibcode:2017JPCRD..46a3107L.doi:10.1063/1.4977429.ISSN0047-2689.PMC5514612.PMID28736460.
- Landau, L. D.;Lifshitz, E.M.(1987).Fluid Mechanics(2nd ed.). Elsevier.ISBN978-0-08-057073-0.Archivedfrom the original on 2020-03-21.Retrieved2019-09-18.
- Maginn, Edward J.; Messerly, Richard A.; Carlson, Daniel J.; Roe, Daniel R.; Elliott, J. Richard (2019)."Best Practices for Computing Transport Properties 1. Self-Diffusivity and Viscosity from Equilibrium Molecular Dynamics [Article v1.0]".Living Journal of Computational Molecular Science.1(1). University of Colorado at Boulder.doi:10.33011/livecoms.1.1.6324.ISSN2575-6524.S2CID104357320.
- Monogenidou, S. A.; Assael, M. J.; Huber, M. L. (2018)."Reference Correlation for the Viscosity of Ammonia from the Triple Point to 725 K and up to 50 MPa".Journal of Physical and Chemical Reference Data.47(2). AIP Publishing: 023102.Bibcode:2018JPCRD..47b3102M.doi:10.1063/1.5036724.ISSN0047-2689.PMC6512859.PMID31092958.
- Lesieur, Marcel (2012).Turbulence in Fluids: Stochastic and Numerical Modelling.Springer.ISBN978-94-009-0533-7.Archivedfrom the original on 2020-03-14.Retrieved2018-11-30.
- Mewis, Jan; Wagner, Norman J. (2012).Colloidal Suspension Rheology.Cambridge University Press.ISBN978-0-521-51599-3.Archivedfrom the original on 2020-03-14.Retrieved2018-12-10.
- McNaught, A. D.; Wilkinson, A. (1997). "poise".IUPAC. Compendium of Chemical Terminology (the "Gold Book" ).S. J. Chalk (2nd ed.). Oxford: Blackwell Scientific.doi:10.1351/goldbook.ISBN0-9678550-9-8.
- Millat, Jorgen (1996).Transport Properties of Fluids: Their Correlation, Prediction and Estimation.Cambridge: Cambridge University Press.ISBN978-0-521-02290-3.OCLC668204060.
- Mueller, S.; Llewellin, E. W.; Mader, H. M. (2009). "The rheology of suspensions of solid particles".Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences.466(2116): 1201–1228.doi:10.1098/rspa.2009.0445.ISSN1364-5021.
- Nič, Miloslav; et al., eds. (1997). "dynamic viscosity,η".IUPAC Compendium of Chemical Terminology.Oxford: Blackwell Scientific Publications.doi:10.1351/goldbook.ISBN978-0-9678550-9-7.
- Ojovan, M.I.; Lee, W.E. (2004). "Viscosity of network liquids within Doremus approach".J. Appl. Phys.95(7): 3803–3810.Bibcode:2004JAP....95.3803O.doi:10.1063/1.1647260.
- Ojovan, M.I.; Travis, K. P.; Hand, R.J. (2007)."Thermodynamic parameters of bonds in glassy materials from viscosity-temperature relationships"(PDF).J. Phys.: Condens. Matter.19(41): 415107.Bibcode:2007JPCM...19O5107O.doi:10.1088/0953-8984/19/41/415107.PMID28192319.S2CID24724512.Archived(PDF)from the original on 2018-07-25.Retrieved2019-09-27.
- Plumb, Robert C. (1989)."Antique windowpanes and the flow of supercooled liquids".Journal of Chemical Education.66(12): 994.Bibcode:1989JChEd..66..994P.doi:10.1021/ed066p994.Archived fromthe originalon 2005-08-26.Retrieved2013-12-25.
- Rapaport, D.C. (2004).The Art of Molecular Dynamics Simulation(2nd ed.). Cambridge University Press.ISBN978-0-521-82568-9.Archivedfrom the original on 2018-06-25.Retrieved2022-01-10.
- Reid, Robert C.; Sherwood, Thomas K. (1958).The Properties of Gases and Liquids.McGraw-Hill.
- Reif, F. (1965),Fundamentals of Statistical and Thermal Physics,McGraw-Hill.An advanced treatment.
- Rosenson, R S; McCormick, A; Uretz, E F (1996-08-01)."Distribution of blood viscosity values and biochemical correlates in healthy adults".Clinical Chemistry.42(8). Oxford University Press (OUP): 1189–1195.doi:10.1093/clinchem/42.8.1189.ISSN0009-9147.PMID8697575.
- Rowland, Darren; Al Ghafri, Saif Z. S.; May, Eric F. (2020-03-01)."Wide-Ranging Reference Correlations for Dilute Gas Transport Properties Based on Ab Initio Calculations and Viscosity Ratio Measurements".Journal of Physical and Chemical Reference Data.49(1). AIP Publishing: 013101.Bibcode:2020JPCRD..49a3101X.doi:10.1063/1.5125100.ISSN0047-2689.S2CID213794612.
- Różańska, S.; Różański, J.; Ochowiak, M.; Mitkowski, P. T. (2014)."Extensional viscosity measurements of concentrated emulsions with the use of the opposed nozzles device"(PDF).Brazilian Journal of Chemical Engineering.31(1): 47–55.doi:10.1590/S0104-66322014000100006.ISSN0104-6632.Archived(PDF)from the original on 2020-05-08.Retrieved2019-09-19.
- Rumble, John R., ed. (2018).CRC Handbook of Chemistry and Physics(99th ed.). Boca Raton, FL: CRC Press.ISBN978-1-138-56163-2.
- Sagdeev, Damir; Gabitov, Il'giz; Isyanov, Chingiz; Khairutdinov, Vener; Farakhov, Mansur; Zaripov, Zufar; Abdulagatov, Ilmutdin (2019-04-22). "Densities and Viscosities of Oleic Acid at Atmospheric Pressure".Journal of the American Oil Chemists' Society.96(6). Wiley: 647–662.doi:10.1002/aocs.12217.ISSN0003-021X.S2CID150156106.
- Scherer, George W.; Pardenek, Sandra A.; Swiatek, Rose M. (1988). "Viscoelasticity in silica gel".Journal of Non-Crystalline Solids.107(1): 14.Bibcode:1988JNCS..107...14S.doi:10.1016/0022-3093(88)90086-5.
- Schroeder, Daniel V. (1999).An Introduction to Thermal Physics.Addison Wesley.ISBN978-0-201-38027-9.Archivedfrom the original on 2020-03-10.Retrieved2018-11-30.
- Sharipov, Felix; Benites, Victor J. (2020-07-01). "Transport coefficients of multi-component mixtures of noble gases based on ab initio potentials: Viscosity and thermal conductivity".Physics of Fluids.32(7). AIP Publishing: 077104.arXiv:2006.08687.Bibcode:2020PhFl...32g7104S.doi:10.1063/5.0016261.ISSN1070-6631.S2CID219708359.
- Sivashinsky, V.; Yakhot, G. (1985). "Negative viscosity effect in large-scale flows".The Physics of Fluids.28(4): 1040.Bibcode:1985PhFl...28.1040S.doi:10.1063/1.865025.
- Streeter, Victor Lyle; Wylie, E. Benjamin; Bedford, Keith W. (1998).Fluid Mechanics.WCB/McGraw Hill.ISBN978-0-07-062537-2.Archivedfrom the original on 2020-03-16.Retrieved2019-09-18.
- Sutherland, William(1893)."LII. The viscosity of gases and molecular force"(PDF).The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science.36(223): 507–531.doi:10.1080/14786449308620508.ISSN1941-5982.Archived(PDF)from the original on 2019-07-20.Retrieved2019-09-18.
- Symon, Keith R. (1971).Mechanics(3rd ed.). Addison-Wesley.ISBN978-0-201-07392-8.Archivedfrom the original on 2020-03-11.Retrieved2019-09-18.
- Trachenko, K.; Brazhkin, V. V. (2020-04-22)."Minimal quantum viscosity from fundamental physical constants".Science Advances.6(17). American Association for the Advancement of Science (AAAS): eaba3747.arXiv:1912.06711.Bibcode:2020SciA....6.3747T.doi:10.1126/sciadv.aba3747.ISSN2375-2548.PMC7182420.PMID32426470.
- Trachenko, Kostya; Brazhkin, Vadim V. (2021-12-01)."The quantum mechanics of viscosity"(PDF).Physics Today.74(12). AIP Publishing: 66–67.Bibcode:2021PhT....74l..66T.doi:10.1063/pt.3.4908.ISSN0031-9228.S2CID244831744.Archived(PDF)from the original on 2022-01-10.Retrieved2022-01-10.
- Trouton, Fred. T. (1906)."On the Coefficient of Viscous Traction and Its Relation to that of Viscosity".Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences.77(519): 426–440.Bibcode:1906RSPSA..77..426T.doi:10.1098/rspa.1906.0038.ISSN1364-5021.
- Velliadou, Danai; Tasidou, Katerina A.; Antoniadis, Konstantinos D.; Assael, Marc J.; Perkins, Richard A.; Huber, Marcia L. (2021-03-25)."Reference Correlation for the Viscosity of Xenon from the Triple Point to 750 K and up to 86 MPa".International Journal of Thermophysics.42(5). Springer Science and Business Media LLC: 74.Bibcode:2021IJT....42...74V.doi:10.1007/s10765-021-02818-9.ISSN0195-928X.PMC8356199.PMID34393314.
- Viswanath, D.S.; Natarajan, G. (1989).Data Book on the Viscosity of Liquids.Hemisphere Publishing Corporation.ISBN0-89116-778-1.
- Viswanath, Dabir S.; et al. (2007).Viscosity of Liquids: Theory, Estimation, Experiment, and Data.Springer.ISBN978-1-4020-5481-5.
- Walzer, Uwe; Hendel, Roland; Baumgardner, John,"Mantle Viscosity and the Thickness of the Convective Downwellings",igw.uni-jena.de,archived fromthe originalon 2007-06-11
- Xie, Hong-Yi; Levchenko, Alex (23 January 2019). "Negative viscosity and eddy flow of the imbalanced electron-hole liquid in graphene".Phys. Rev. B.99(4): 045434.arXiv:1807.04770.Bibcode:2019PhRvB..99d5434X.doi:10.1103/PhysRevB.99.045434.S2CID51792702.
- Yanniotis, S.; Skaltsi, S.; Karaburnioti, S. (February 2006). "Effect of moisture content on the viscosity of honey at different temperatures".Journal of Food Engineering.72(4): 372–377.doi:10.1016/j.jfoodeng.2004.12.017.
- Zhao, Mengjing; Wang, Yong; Yang, Shufeng; Li, Jingshe; Liu, Wei; Song, Zhaoqi (2021)."Flow behavior and heat transfer of molten steel in a two-strand tundish heated by plasma".Journal of Materials Research and Technology.13.Elsevier BV: 561–572.doi:10.1016/j.jmrt.2021.04.069.ISSN2238-7854.S2CID236277034.
- Zhmud, Boris (2014)."Viscosity Blending Equations"(PDF).Lube-Tech:93.Lube.No. 121. pp. 22–27.Archived(PDF)from the original on 2018-12-01.Retrieved2018-11-30.
- "NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP): Version 10".NIST.2018-01-01.Archivedfrom the original on 2021-12-16.Retrieved2021-12-23.
- tec-science (2020-03-25)."Viscosity of liquids and gases".tec-science.Archivedfrom the original on 2020-04-19.Retrieved2020-05-07.
External links
[edit]- Viscosity - The Feynman Lectures on Physics
- Fluid properties– high accuracy calculation of viscosity for frequently encountered pure liquids and gases
- Fluid Characteristics Chart– a table of viscosities and vapor pressures for various fluids
- Gas Dynamics Toolbox– calculate coefficient of viscosity for mixtures of gases
- Glass Viscosity Measurement– viscosity measurement, viscosity units and fixpoints, glass viscosity calculation
- Kinematic Viscosity– conversion between kinematic and dynamic viscosity
- Physical Characteristics of Water– a table of water viscosity as a function of temperature
- Calculation of temperature-dependent dynamic viscosities for some common components
- Artificial viscosity
- Viscosity of Air, Dynamic and Kinematic, Engineers Edge










![{\displaystyle [\mu ]={\frac {\rm {kg}}{\rm {m{\cdot }s}}}={\frac {\rm {N}}{\rm {m^{2}}}}{\cdot }{\rm {s}}={\rm {Pa{\cdot }s}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0505c4de127e4d762cc7174f9e205606cbef004)









![{\displaystyle [\nu ]=\mathrm {\frac {m^{2}}{s}} =\mathrm {{\frac {N{\cdot }m}{kg}}{\cdot }s} =\mathrm {{\frac {J}{kg}}{\cdot }s} =}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abefedddb99ec0896354cfcfcdffd26d00903265)













![{\displaystyle {\boldsymbol {\tau }}=\mu \left[\nabla \mathbf {v} +(\nabla \mathbf {v} )^{\mathrm {T} }\right]-\left({\frac {2}{3}}\mu -\kappa \right)(\nabla \cdot \mathbf {v} )\mathbf {\delta } ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c881ede5c0e043dbe36b7b5a30b4c6bf92204e5a)




![{\displaystyle {\begin{aligned}\mathbf {J} &=-D{\frac {\partial \rho }{\partial x}}&&{\text{(Fick's law of diffusion)}}\\[5pt]\mathbf {q} &=-k_{t}{\frac {\partial T}{\partial x}}&&{\text{(Fourier's law of heat conduction)}}\\[5pt]\tau &=\mu {\frac {\partial u}{\partial y}}&&{\text{(Newton's law of viscosity)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6380b89b0d24d9c9deb9ef04f333430b073c45cc)

































































![{\displaystyle \mu =AT\exp \left({\frac {B}{RT}}\right)\left[1+C\exp \left({\frac {D}{RT}}\right)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38aa9224e9ac73624655cd20405e140af63a62eb)
![{\displaystyle \mu =\exp {\left\{{\frac {V_{c}C_{G}}{k_{B}T}}\exp {\left[(2+\lambda )\alpha _{T}T_{g}\left(1-{\frac {T}{T_{g}}}\right)\right]}\right\}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7c6670713177337446c22a7976e9664d2008526)








