Olog

The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.

The theory ofologsis an attempt to provide a rigorous mathematical framework for knowledge representation, construction of scientific models and data storage usingcategory theory,linguistic and graphical tools. Ologs were introduced in 2012 byDavid Spivakand Robert Kent.^[1]

Etymology

The term "olog" is short for "ontologylog "." Ontology "derives fromonto-,from theGreekὤν,ὄντος"being; that which is", present participle of the verbεἰμί"be", and-λογία,-logia:science,study,theory.

Mathematical formalism

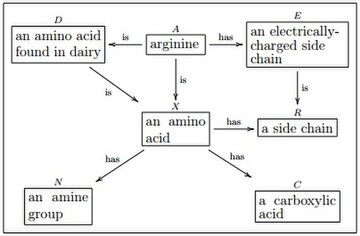
An olog ${\mathcal {C}}$ for a given domain is acategorywhoseobjectsare boxes labeled with phrases (more specifically, singular indefinite noun phrases) relevant to the domain, and whosemorphismsare directed arrows between the boxes, labeled with verb phrases also relevant to the domain. These noun and verb phrases combine to form sentences that express relationships between objects in the domain.

In every olog, the objects exist within atarget category.Unless otherwise specified, the target category is taken to be ${\textbf {Set}}$ ,thecategory of sets and functions. The boxes in the above diagram represent objects of ${\textbf {Set}}$ .For example, the box containing the phrase "an amino acid" represents the set of all amino acids, and the box containing the phrase "a side chain" represents the set of all side chains. The arrow labeled "has" that points from "an amino acid" to "a side chain" represents the function that maps each amino acid to its unique side chain.

Another target category that can be used is theKleisli category ${\mathcal {C}}_{\mathbb {P} }$ of thepower set monad.Given an $A\in Ob({\textbf {Set}})$ , $\mathbb {P} (A)$ is then the power set of A. Thenatural transformation $\eta$ maps $a\in A$ to thesingleton $\{a\}$ ,and the natural transformation $\mu$ maps a set of sets to its union. TheKleisli category ${\mathcal {C}}_{\mathbb {P} }$ is the category with the objects matching those in $\mathbb {P}$ ,and morphisms that establishbinary relations.Given a morphism $f:A\to B$ ,and given $a\in A$ and $b\in B$ ,we define the morphism $R$ by saying that $(a,b)\in R$ whenever $b\in f(a)$ .The verb phrases used with this target category would need to make sense with objects that are subsets: for example, "is related to" or "is greater than".

Another possible target category is the Kleisli category of probability distributions, called the Giry monad.^[2]This provides a generalization ofMarkov decision processes.

Ologs and databases

An olog ${\mathcal {C}}$ can also be viewed as adatabase schema.Every box (object of ${\mathcal {C}}$ ) in the olog is atable $T$ and the arrows (morphisms) emanating from the box are columns in ${\mathcal {C}}$ .The assignment of a particular instance to an object of ${\mathcal {C}}$ is done through afunctor $I:{\mathcal {C}}\to {\textbf {Set}}$ .In the example above, the box "an amino acid" will be represented as a table whose number of rows is equal to the number of types of amino acids and whose number of columns is three, one column for each arrow emanating from that box.

Relations between ologs

"Communication" between different ologs which in practice can be communication between different models or world-views is done usingfunctors.Spivak coins the notions of a 'meaningful' and 'strongly meaningful' functors.^[1]Let ${\mathcal {C}}$ and ${\mathcal {D}}$ be two ologs, $I:{\mathcal {C}}\to {\textbf {Set}}$ , $J:{\mathcal {D}}\to {\textbf {Set}}$ functors (see the section on ologs and databases) and $F:{\mathcal {C}}\to {\mathcal {D}}$ a functor. $F$ is called aschema mapping.We say that a $F$ ismeaningfulif there exists a natural transformation $m:I\to F^{*}J$ (thepullbackof J by F).

Taking as an example ${\mathcal {C}}$ and ${\mathcal {D}}$ as two different scientific models, the functor $F$ is meaningful if "predictions", which are objects in ${\textbf {Set}}$ ,made by the first model ${\mathcal {C}}$ can be translated to the second model ${\mathcal {D}}$ .

We say that $F$ isstrongly meaningfulif given an object $X\in {\mathcal {C}}$ we have $I(X)=J(F(X))$ .This equality is equivalent to requiring $m$ to be a natural isomorphism.

Sometimes it will be hard to find a meaningful functor $F$ from ${\mathcal {C}}$ to ${\mathcal {D}}$ .In such a case we may try to define a new olog ${\mathcal {B}}$ which represents the common ground of ${\mathcal {C}}$ and ${\mathcal {D}}$ and find meaningful functors $F_{\mathcal {C}}:{\mathcal {B}}\to {\mathcal {C}}$ and $F_{\mathcal {D}}:{\mathcal {B}}\to {\mathcal {D}}$ .

If communication between ologs is limited to a two-way communication as described above then we may think of a collection of ologs as nodes of agraphand of the edges as functors connecting the ologs. If a simultaneous communication between more than two ologs is allowed then the graph becomes a symmetricsimplicial complex.

Rules of good practice

Spivak provides some rules of good practice for writing an olog whose morphisms have a functional nature (see the first example in the section Mathematical formalism).^[1]The text in a box should adhere to the following rules:

begin with the word "a" or "an". (Example: "an amino acid" ).
refer to a distinction made and recognizable by the olog's author.
refer to a distinction for which there is well defined functor whose range is ${\textbf {Set}}$ ,i.e. an instance can be documented. (Example: there is a set of all amino acids).
declare all variables in a compound structure. (Example: instead of writing in a box "a man and a woman" write "a man $m$ and a woman $w$ "or" a pair $(m,w)$ where $m$ is a man and $w$ is a woman ").

The first three rules ensure that the objects (the boxes) defined by the olog's author are well-defined sets. The fourth rule improves the labeling of arrows in an olog.

Applications

This concept was used in a paper published in the December 2011 issue ofBioNanoScienceby David Spivak and others to establish a scientific analogy between spider silk and musical composition.^[3]

References

^^a ^b ^cSpivak, David I.; Kent, Robert E. (31 January 2012)."Ologs: A Categorical Framework for Knowledge Representation".PLOS ONE.7(1): e24274.arXiv:1102.1889.Bibcode:2012PLoSO...724274S.doi:10.1371/journal.pone.0024274.PMC3269434.PMID 22303434.
^Giry monadat thenLab
^Giesa, Tristan; Spivak, David I.; Buehler, Markus J. (2011). "Reoccurring patterns in hierarchical protein materials and music: The power of analogies".BioNanoScience.1(4): 153–161.arXiv:1111.5297.doi:10.1007/s12668-011-0022-5.S2CID 5178100.

External links

Spivak, David I."Categorical informatics".math.mit.edu.Retrieved2 May2017.
Spivak, David I. (2014).Category theory for the sciences.Cambridge, MA:MIT Press.ISBN 9780262028134.OCLC 876833252.

[Spivak-1] Spivak, David I.; Kent, Robert E. (31 January 2012)."Ologs: A Categorical Framework for Knowledge Representation".PLOS ONE.7(1): e24274.arXiv:1102.1889.Bibcode:2012PLoSO...724274S.doi:10.1371/journal.pone.0024274.PMC3269434.PMID 22303434.

[2] Giry monadat thenLab

[3] Giesa, Tristan; Spivak, David I.; Buehler, Markus J. (2011). "Reoccurring patterns in hierarchical protein materials and music: The power of analogies".BioNanoScience.1(4): 153–161.arXiv:1111.5297.doi:10.1007/s12668-011-0022-5.S2CID 5178100.

[1]

[2]

[3]