2 41polytope

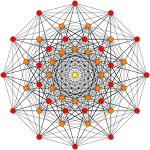421	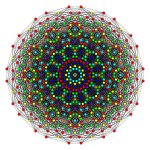142	241
Rectified 421	Rectified 142	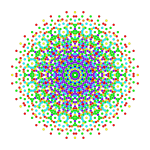Rectified 241
Birectified 421	Trirectified 421
Orthogonal projectionsin E6Coxeter plane

In 8-dimensionalgeometry,the2₄₁is auniform 8-polytope,constructed within the symmetry of theE₈group.

ItsCoxeter symbolis2₄₁,describing its bifurcatingCoxeter-Dynkin diagram,with a single ring on the end of the 2-node sequences.

Therectified 2₄₁is constructed by points at the mid-edges of the2₄₁.Thebirectified 2₄₁is constructed by points at the triangle face centers of the2₄₁,and is the same as therectified 1₄₂.

These polytopes are part of a family of 255 (2⁸− 1) convexuniform polytopesin 8-dimensions, made ofuniform polytopefacets, defined by all permutations of rings in thisCoxeter-Dynkin diagram:.

2₄₁polytope

241polytope
Type	Uniform8-polytope
Family	2k1polytope
Schläfli symbol	{3,3,34,1}
Coxeter symbol	241
Coxeter diagram
7-faces	17520: 240231 17280{36}
6-faces	144960: 6720221 138240{35}
5-faces	544320: 60480211 483840{34}
4-faces	1209600: 241920{201 967680{33}
Cells	1209600{32}
Faces	483840{3}
Edges	69120
Vertices	2160
Vertex figure	141
Petrie polygon	30-gon
Coxeter group	E8,[34,2,1]
Properties	convex

The2₄₁is composed of 17,520facets(2402₃₁polytopes and 17,2807-simplices), 144,9606-faces(6,7202₂₁polytopes and 138,2406-simplices), 544,320 5-faces (60,4802₁₁and 483,8405-simplices), 1,209,6004-faces(4-simplices), 1,209,600 cells (tetrahedra), 483,840faces(triangles), 69,120edges,and 2160vertices.Itsvertex figureis a7-demicube.

This polytope is a facet in theuniform tessellation, 2₅₁withCoxeter-Dynkin diagram:

Alternate names

• E. L. Eltenamed it V₂₁₆₀(for its 2160 vertices) in his 1912 listing of semiregular polytopes.
• It is named2₄₁byCoxeterfor its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 2-node sequence.
• Diacositetracont-myriaheptachiliadiacosioctaconta-zetton(Acronym Bay) - 240-17280 facetted polyzetton (Jonathan Bowers)

The 2160 vertices can be defined as follows:

16 permutations of (±4,0,0,0,0,0,0,0) of (8-orthoplex)

1120 permutations of (±2,±2,±2,±2,0,0,0,0) of (trirectified 8-orthoplex)

1024 permutations of (±3,±1,±1,±1,±1,±1,±1,±1)with an odd number of minus-signs

Construction

It is created by aWythoff constructionupon a set of 8hyperplanemirrors in 8-dimensional space.

The facet information can be extracted from itsCoxeter-Dynkin diagram:.

Removing the node on the short branch leaves the7-simplex:.There are 17280 of these facets

Removing the node on the end of the 4-length branch leaves the2₃₁,.There are 240 of these facets. They are centered at the positions of the 240 vertices in the4₂₁polytope.

Thevertex figureis determined by removing the ringed node and ringing the neighboring node. This makes the7-demicube,1₄₁,.

Seen in aconfiguration matrix,the element counts can be derived by mirror removal and ratios ofCoxeter grouporders.

		Configuration matrix
E8		k-face	fk	f0	f1	f2	f3	f4		f5		f6		f7		k-figure	notes
D7		( )	f0	2160	64	672	2240	560	2240	280	1344	84	448	14	64	h{4,3,3,3,3,3}	E8/D7= 192*10!/64/7! = 2160
A6A1		{ }	f1	2	69120	21	105	35	140	35	105	21	42	7	7	r{3,3,3,3,3}	E8/A6A1= 192*10!/7!/2 = 69120
A4A2A1		{3}	f2	3	3	483840	10	5	20	10	20	10	10	5	2	{}x{3,3,3}	E8/A4A2A1= 192*10!/5!/3!/2 = 483840
A3A3		{3,3}	f3	4	6	4	1209600	1	4	4	6	6	4	4	1	{3,3}V( )	E8/A3A3= 192*10!/4!/4! = 1209600
A4A3		{3,3,3}	f4	5	10	10	5	241920	*	4	0	6	0	4	0	{3,3}	E8/A4A3= 192*10!/5!/4! = 241920
A4A2				5	10	10	5	*	967680	1	3	3	3	3	1	{3}V( )	E8/A4A2= 192*10!/5!/3! = 967680
D5A2		{3,3,31,1}	f5	10	40	80	80	16	16	60480	*	3	0	3	0	{3}	E8/D5A2= 192*10!/16/5!/2 = 40480
A5A1		{3,3,3,3}		6	15	20	15	0	6	*	483840	1	2	2	1	{ }V( )	E8/A5A1= 192*10!/6!/2 = 483840
E6A1		{3,3,32,1}	f6	27	216	720	1080	216	432	27	72	6720	*	2	0	{ }	E8/E6A1= 192*10!/72/6! = 6720
A6		{3,3,3,3,3}		7	21	35	35	0	21	0	7	*	138240	1	1		E8/A6= 192*10!/7! = 138240
E7		{3,3,33,1}	f7	126	2016	10080	20160	4032	12096	756	4032	56	576	240	*	( )	E8/E7= 192*10!/72!/8! = 240
A7		{3,3,3,3,3,3}		8	28	56	70	0	56	0	28	0	8	*	17280		E8/A7= 192*10!/8! = 17280

Visualizations

The projection of2₄₁to theE₈Coxeter plane (aka. the Petrie projection) with polytope radius$2{\sqrt {2}}$and 69120 edges of length$2{\sqrt {2}}$

Shown in 3D projection using the basis vectors [u,v,w] giving H3 symmetry:

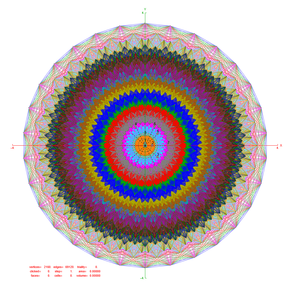
• u = (1,φ,0, −1,φ,0,0,0)
• v = (φ,0, 1,φ,0, −1,0,0)
• w = (0, 1,φ,0, −1,φ,0,0)

The 2160 projected 2₄₁polytope vertices are sorted and tallied by their 3D norm generating the increasingly transparent hulls for each set of tallied norms. The overlapping vertices are color coded by overlap count. Also shown is a list of each hull group, the normed distance from the origin, and the number of vertices in the group.

The 2160 projected 2₄₁polytope projected to 3D (as above) with each normed hull group listed individually with vertex counts. Notice the last two outer hulls are a combination of two overlapped Icosahedrons (24) and a Icosidodecahedron (30).

E8 [30]	[20]	[24]
(1)
E7 [18]	E6 [12]	[6]
	(1,8,24,32)

Petrie polygonprojections are 12, 18, or 30-sided based on the E6, E7, and E8 symmetries (respectively). The 2160 vertices are all displayed, but lower symmetry forms have projected positions overlapping, shown as different colored vertices. For comparison, a B6 coxeter group is also shown.

D3 / B2 / A3 [4]	D4 / B3 / A2 [6]	D5 / B4 [8]
D6 / B5 / A4 [10]	D7 / B6 [12]	D8 / B7 / A6 [14]
	(1,3,9,12,18,21,36)
B8 [16/2]	A5 [6]	A7 [8]

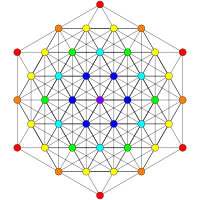
Related polytopes and honeycombs

2k1figuresinndimensions
Space	Finite						Euclidean	Hyperbolic
n	3	4	5	6	7	8	9	10
Coxeter group	E3=A2A1	E4=A4	E5=D5	E6	E7	E8	E9=${\tilde {E}}_{8}$= E8+	E10=${\bar {T}}_{8}$= E8++
Coxeter diagram
Symmetry	[3−1,2,1]	[30,2,1]	[[31,2,1]]	[32,2,1]	[33,2,1]	[34,2,1]	[35,2,1]	[36,2,1]
Order	12	120	384	51,840	2,903,040	696,729,600	∞
Graph							-	-
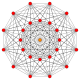
Name	2−1,1	201	211	221	231	241	251	261

Rectified 2_41 polytope

Rectified 241polytope
Type	Uniform8-polytope
Schläfli symbol	t1{3,3,34,1}
Coxeter symbol	t1(241)
Coxeter diagram
7-faces	19680 total: 240t1(221) 17280t1{36} 2160141
6-faces	313440
5-faces	1693440
4-faces	4717440
Cells	7257600
Faces	5322240
Edges	19680
Vertices	69120
Vertex figure	rectified 6-simplexprism
Petrie polygon	30-gon
Coxeter group	E8,[34,2,1]
Properties	convex

Therectified 2₄₁is arectificationof the 2₄₁polytope, with vertices positioned at the mid-edges of the 2₄₁.

Alternate names

• Rectified Diacositetracont-myriaheptachiliadiacosioctaconta-zetton for rectified 240-17280 facetted polyzetton (known as robay for short)

Construction

It is created by aWythoff constructionupon a set of 8hyperplanemirrors in 8-dimensional space, defined by root vectors of theE₈Coxeter group.

The facet information can be extracted from itsCoxeter-Dynkin diagram:.

Removing the node on the short branch leaves therectified 7-simplex:.

Removing the node on the end of the 4-length branch leaves therectified 2₃₁,.

Removing the node on the end of the 2-length branch leaves the7-demicube,1₄₁.

Thevertex figureis determined by removing the ringed node and ringing the neighboring node. This makes therectified 6-simplexprism,.

Visualizations

Petrie polygonprojections are 12, 18, or 30-sided based on the E6, E7, and E8 symmetries (respectively). The 2160 vertices are all displayed, but lower symmetry forms have projected positions overlapping, shown as different colored vertices. For comparison, a B6 coxeter group is also shown.

E8 [30]	[20]	[24]
(1)
E7 [18]	E6 [12]	[6]
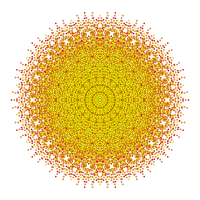
	(1,8,24,32)

D3 / B2 / A3 [4]	D4 / B3 / A2 [6]	D5 / B4 [8]
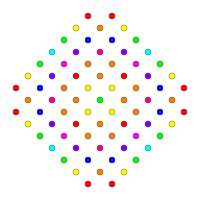
D6 / B5 / A4 [10]	D7 / B6 [12]	D8 / B7 / A6 [14]
	(1,3,9,12,18,21,36)
B8 [16/2]	A5 [6]	A7 [8]

See also

• List of E8 polytopes

References

• Elte, E. L. (1912),The Semiregular Polytopes of the Hyperspaces,Groningen: University of Groningen
• H. S. M. Coxeter,Regular Polytopes,3rd Edition, Dover New York, 1973
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter,edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,ISBN978-0-471-01003-6[1]
  • (Paper 24) H.S.M. Coxeter,Regular and Semi-Regular Polytopes III,[Math. Zeit. 200 (1988) 3-45]
• Klitzing, Richard."8D Uniform polyzetta".x3o3o3o *c3o3o3o3o - bay, o3x3o3o *c3o3o3o3o - robay