Addition

For other uses, seeAddition (disambiguation).

"Add" redirects here. For other uses, seeADD (disambiguation).

3 + 2 = 5 withapples,a popular choice in textbooks

Addition(usually signified by theplus symbol+) is one of the four basicoperationsofarithmetic,the other three beingsubtraction,multiplicationanddivision.The addition of twowhole numbersresults in the total amount orsumof those values combined. The example in the adjacent image shows two columns of three apples and two apples each, totaling at five apples. This observation is equivalent to themathematical expression"3 + 2 = 5"(that is, "3plus2 isequalto 5 ").

Besidescountingitems, addition can also be defined and executed without referring toconcrete objects,using abstractions callednumbersinstead, such asintegers,real numbersandcomplex numbers.Addition belongs to arithmetic, a branch ofmathematics.Inalgebra,another area of mathematics, addition can also be performed on abstract objects such asvectors,matrices,subspacesandsubgroups.

Addition has several important properties. It iscommutative,meaning that the order of theoperandsdoes not matter, and it isassociative,meaning that when one adds more than two numbers, the order in which addition is performed does not matter. Repeated addition of1is the same as counting (seeSuccessor function). Addition of0does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.

Performing addition is one of the simplest numerical tasks to do. Addition of very small numbers is accessible to toddlers; the most basic task,1 + 1,can be performed by infants as young as five months, and even some members of other animal species. Inprimary education,students are taught to add numbers in thedecimalsystem, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancientabacusto the moderncomputer,where research on the most efficient implementations of addition continues to this day.

Notation and terminology

The plus sign

Addition is written using theplus sign"+" between the terms;that is, ininfix notation.The result is expressed with anequals sign.For example,

$1+2=3$( "one plus two equals three" )

$5+4+2=11$(see "associativity"below)

$3+3+3+3=12$(see "multiplication"below)

Columnar addition – the numbers in the column are to be added, with the sum written below theunderlinednumber.

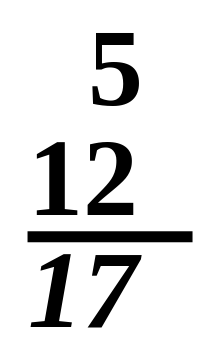
There are also situations where addition is "understood", even though no symbol appears:

• A whole number followed immediately by afractionindicates the sum of the two, called amixed number.For example,$$3{\frac {1}{2}}=3+{\frac {1}{2}}=3.5.$$This notation can cause confusion, since in most other contexts,juxtapositiondenotesmultiplicationinstead.

The sum of aseriesof related numbers can be expressed throughcapital sigma notation,which compactly denotesiteration.For example,

$\sum _{k=1}^{5}k^{2}=1^{2}+2^{2}+3^{2}+4^{2}+5^{2}=55.$

Terms

The numbers or the objects to be added in general addition are collectively referred to as theterms,theaddendsor thesummands;this terminology carries over to the summation of multiple terms. This is to be distinguished fromfactors,which aremultiplied. Some authors call the first addend theaugend.In fact, during theRenaissance,many authors did not consider the first addend an "addend" at all. Today, due to thecommutative propertyof addition, "augend" is rarely used, and both terms are generally called addends.

All of the above terminology derives fromLatin."Addition"and"add"areEnglishwords derived from the Latinverbaddere,which is in turn acompoundofad"to" anddare"to give", from theProto-Indo-European root*deh₃-"to give"; thus toaddis togive to.Using thegerundivesuffix-ndresults in "addend", "thing to be added".Likewise fromaugere"to increase", one gets "augend", "thing to be increased".

Redrawn illustration fromThe Art of Nombryng,one of the first English arithmetic texts, in the 15th century.

"Sum" and "summand" derive from the Latinnounsumma"the highest, the top" and associated verbsummare.This is appropriate not only because the sum of two positive numbers is greater than either, but because it was common for theancient GreeksandRomansto add upward, contrary to the modern practice of adding downward, so that a sum was literally higher than the addends. Addereandsummaredate back at least toBoethius,if not to earlier Roman writers such asVitruviusandFrontinus;Boethius also used several other terms for the addition operation. The laterMiddle Englishterms "adden" and "adding" were popularized byChaucer.

Theplus sign"+" (Unicode:U+002B;ASCII:+) is an abbreviation of the Latin wordet,meaning "and".It appears in mathematical works dating back to at least 1489.

Interpretations

Addition is used to model many physical processes. Even for the simple case of addingnatural numbers,there are many possible interpretations and even more visual representations.

Combining sets

One set has 3 shapes while the other set has 2. The total amount of shapes are 5, which is a consequence of the addition of the objects from the two sets (3 + 2 = 5).

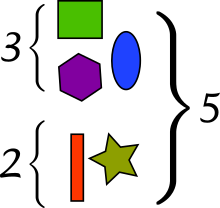
Possibly the most basic interpretation of addition lies in combiningsets:

• When two or more disjoint collections are combined into a single collection, the number of objects in the single collection is the sum of the numbers of objects in the original collections.

This interpretation is easy to visualize, with little danger of ambiguity. It is also useful in higher mathematics (for the rigorous definition it inspires, see§ Natural numbersbelow). However, it is not obvious how one should extend this version of addition to include fractional numbers or negative numbers.

One possible fix is to consider collections of objects that can be easily divided, such as pies or, still better, segmented rods.Rather than solely combining collections of segments, rods can be joined end-to-end, which illustrates another conception of addition: adding not the rods but the lengths of the rods.

Extending a length

A number-line visualization of the algebraic addition 2 + 4 = 6. A "jump" that has a distance of 2 followed by another that is long as 4, is the same as a translation by 6.

A number-line visualization of the unary addition 2 + 4 = 6. A translation by 4 is equivalent to four translations by 1.

A second interpretation of addition comes from extending an initial length by a given length:

• When an original length is extended by a given amount, the final length is the sum of the original length and the length of the extension.

The suma+bcan be interpreted as abinary operationthat combinesaandb,in an algebraic sense, or it can be interpreted as the addition ofbmore units toa.Under the latter interpretation, the parts of a suma+bplay asymmetric roles, and the operationa+bis viewed as applying theunary operation+btoa.Instead of calling bothaandbaddends, it is more appropriate to callatheaugendin this case, sinceaplays a passive role. The unary view is also useful when discussingsubtraction,because each unary addition operation has an inverse unary subtraction operation, andvice versa.

Properties

Commutativity

4 + 2 = 2 + 4 with blocks

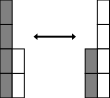
Addition iscommutative,meaning that one can change the order of the terms in a sum, but still get the same result. Symbolically, ifaandbare any two numbers, then

a+b=b+a.

The fact that addition is commutative is known as the "commutative law of addition" or "commutative property of addition". Some otherbinary operationsare commutative, such as multiplication, but many others, such as subtraction and division, are not.

Associativity

2 + (1 + 3) = (2 + 1) + 3 with segmented rods

Addition isassociative,which means that when three or more numbers are added together, theorder of operationsdoes not change the result.

As an example, should the expressiona+b+cbe defined to mean (a+b) +cora+ (b+c)? Given that addition is associative, the choice of definition is irrelevant. For any three numbersa,b,andc,it is true that(a+b) +c=a+ (b+c).For example,(1 + 2) + 3 = 3 + 3 = 6 = 1 + 5 = 1 + (2 + 3).

When addition is used together with other operations, theorder of operationsbecomes important. In the standard order of operations, addition is a lower priority thanexponentiation,nth roots,multiplication and division, but is given equal priority to subtraction.

Identity element

5 + 0 = 5 with bags of dots

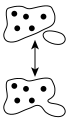
Addingzeroto any number, does not change the number; this means that zero is theidentity elementfor addition, and is also known as theadditive identity.In symbols, for everya,one has

a+ 0 = 0 +a=a.

This law was first identified inBrahmagupta'sBrahmasphutasiddhantain 628 AD, although he wrote it as three separate laws, depending on whetherais negative, positive, or zero itself, and he used words rather than algebraic symbols. LaterIndian mathematiciansrefined the concept; around the year 830,Mahavirawrote, "zero becomes the same as what is added to it", corresponding to the unary statement0 +a=a.In the 12th century,Bhaskarawrote, "In the addition of cipher, or subtraction of it, the quantity, positive or negative, remains the same", corresponding to the unary statementa+ 0 =a.

Successor

Within the context of integers, addition ofonealso plays a special role: for any integera,the integer(a+ 1)is the least integer greater thana,also known as thesuccessorofa.For instance, 3 is the successor of 2 and 7 is the successor of 6. Because of this succession, the value ofa+bcan also be seen as thebth successor ofa,making addition iterated succession. For example,6 + 2is 8, because 8 is the successor of 7, which is the successor of 6, making 8 the 2nd successor of 6.

Units

To numerically add physical quantities withunits,they must be expressed with common units.For example, adding 50 milliliters to 150 milliliters gives 200 milliliters. However, if a measure of 5 feet is extended by 2 inches, the sum is 62 inches, since 60 inches is synonymous with 5 feet. On the other hand, it is usually meaningless to try to add 3 meters and 4 square meters, since those units are incomparable; this sort of consideration is fundamental indimensional analysis.

Performing addition

Innate ability

Studies on mathematical development starting around the 1980s have exploited the phenomenon ofhabituation:infantslook longer at situations that are unexpected.A seminal experiment byKaren Wynnin 1992 involvingMickey Mousedolls manipulated behind a screen demonstrated that five-month-old infantsexpect1 + 1to be 2, and they are comparatively surprised when a physical situation seems to imply that1 + 1is either 1 or 3. This finding has since been affirmed by a variety of laboratories using different methodologies.Another 1992 experiment with oldertoddlers,between 18 and 35 months, exploited their development of motor control by allowing them to retrieveping-pongballs from a box; the youngest responded well for small numbers, while older subjects were able to compute sums up to 5.

Even some nonhuman animals show a limited ability to add, particularlyprimates.In a 1995 experiment imitating Wynn's 1992 result (but usingeggplantsinstead of dolls),rhesus macaqueandcottontop tamarinmonkeys performed similarly to human infants. More dramatically, after being taught the meanings of theArabic numerals0 through 4, onechimpanzeewas able to compute the sum of two numerals without further training.More recently,Asian elephantshave demonstrated an ability to perform basic arithmetic.

Childhood learning

Typically, children first mastercounting.When given a problem that requires that two items and three items be combined, young children model the situation with physical objects, often fingers or a drawing, and then count the total. As they gain experience, they learn or discover the strategy of "counting-on": asked to find two plus three, children count three past two, saying "three, four,five"(usually ticking off fingers), and arriving at five. This strategy seems almost universal; children can easily pick it up from peers or teachers.Most discover it independently. With additional experience, children learn to add more quickly by exploiting the commutativity of addition by counting up from the larger number, in this case, starting with three and counting "four,five."Eventually children begin to recall certain addition facts ("number bonds"), either through experience or rote memorization. Once some facts are committed to memory, children begin to derive unknown facts from known ones. For example, a child asked to add six and seven may know that6 + 6 = 12and then reason that6 + 7is one more, or 13.Such derived facts can be found very quickly and most elementary school students eventually rely on a mixture of memorized and derived facts to add fluently.

Different nations introduce whole numbers and arithmetic at different ages, with many countries teaching addition in pre-school.However, throughout the world, addition is taught by the end of the first year of elementary school.

Table

Children are often presented with the addition table of pairs of numbers from 0 to 9 to memorize. Knowing this, children can perform any addition.

+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	10
2	2	3	4	5	6	7	8	9	10	11
3	3	4	5	6	7	8	9	10	11	12
4	4	5	6	7	8	9	10	11	12	13
5	5	6	7	8	9	10	11	12	13	14
6	6	7	8	9	10	11	12	13	14	15
7	7	8	9	10	11	12	13	14	15	16
8	8	9	10	11	12	13	14	15	16	17
9	9	10	11	12	13	14	15	16	17	18

Decimal system

The prerequisite to addition in thedecimalsystem is the fluent recall or derivation of the 100 single-digit "addition facts". One couldmemorizeall the facts byrote,but pattern-based strategies are more enlightening and, for most people, more efficient:

• Commutative property:Mentioned above, using the patterna + b = b + areduces the number of "addition facts" from 100 to 55.
• One or two more:Adding 1 or 2 is a basic task, and it can be accomplished through counting on or, ultimately,intuition.
• Zero:Since zero is the additive identity, adding zero is trivial. Nonetheless, in the teaching of arithmetic, some students are introduced to addition as a process that always increases the addends;word problemsmay help rationalize the "exception" of zero.
• Doubles:Adding a number to itself is related to counting by two and tomultiplication.Doubles facts form a backbone for many related facts, and students find them relatively easy to grasp.
• Near-doubles:Sums such as 6 + 7 = 13 can be quickly derived from the doubles fact6 + 6 = 12by adding one more, or from7 + 7 = 14but subtracting one.
• Five and ten:Sums of the form 5 +xand 10 +xare usually memorized early and can be used for deriving other facts. For example,6 + 7 = 13can be derived from5 + 7 = 12by adding one more.
• Making ten:An advanced strategy uses 10 as an intermediate for sums involving 8 or 9; for example,8 + 6 = 8 + 2 + 4 =10 + 4 = 14.

As students grow older, they commit more facts to memory, and learn to derive other facts rapidly and fluently. Many students never commit all the facts to memory, but can still find any basic fact quickly.

Carry

Main article:Carry (arithmetic)

The standard algorithm for adding multidigit numbers is to align the addends vertically and add the columns, starting from the ones column on the right. If a column exceeds nine, the extra digit is "carried"into the next column. For example, in the addition27 + 59

¹
27
+ 59
————
86

7 + 9 = 16, and the digit 1 is the carry.An alternate strategy starts adding from the most significant digit on the left; this route makes carrying a little clumsier, but it is faster at getting a rough estimate of the sum. There are many alternative methods.

Since the end of the 20th century, some US programs, including TERC, decided to remove the traditional transfer method from their curriculum.This decision was criticized,which is why some states and counties did not support this experiment.

Decimal fractions

Decimal fractionscan be added by a simple modification of the above process.One aligns two decimal fractions above each other, with the decimal point in the same location. If necessary, one can add trailing zeros to a shorter decimal to make it the same length as the longer decimal. Finally, one performs the same addition process as above, except the decimal point is placed in the answer, exactly where it was placed in the summands.

As an example, 45.1 + 4.34 can be solved as follows:

4 5. 1 0
+ 0 4. 3 4
————————————
4 9. 4 4

Scientific notation

Main article:Scientific notation § Basic operations

Inscientific notation,numbers are written in the form$x=a\times 10^{b}$,where$a$is the significand and$10^{b}$is the exponential part. Addition requires two numbers in scientific notation to be represented using the same exponential part, so that the two significands can simply be added.

For example:

$2.34\times 10^{-5}+5.67\times 10^{-6}=2.34\times 10^{-5}+0.567\times 10^{-5}=2.907\times 10^{-5}$

Non-decimal

Main article:Binary addition

Addition in other bases is very similar to decimal addition. As an example, one can consider addition in binary.Adding two single-digit binary numbers is relatively simple, using a form of carrying:

0 + 0 → 0

0 + 1 → 1

1 + 0 → 1

1 + 1 → 0, carry 1 (since 1 + 1 = 2 = 0 + (1 × 2¹))

Adding two "1" digits produces a digit "0", while 1 must be added to the next column. This is similar to what happens in decimal when certain single-digit numbers are added together; if the result equals or exceeds the value of the radix (10), the digit to the left is incremented:

5 + 5 → 0, carry 1 (since 5 + 5 = 10 = 0 + (1 × 10¹))

7 + 9 → 6, carry 1 (since 7 + 9 = 16 = 6 + (1 × 10¹))

This is known ascarrying.When the result of an addition exceeds the value of a digit, the procedure is to "carry" the excess amount divided by the radix (that is, 10/10) to the left, adding it to the next positional value. This is correct since the next position has a weight that is higher by a factor equal to the radix. Carrying works the same way in binary:

1 1 1 1 1 (carried digits)
0 1 1 0 1
+ 1 0 1 1 1
—————————————
1 0 0 1 0 0 = 36

In this example, two numerals are being added together: 01101₂(13₁₀) and 10111₂(23₁₀). The top row shows the carry bits used. Starting in the rightmost column,1 + 1 = 10₂.The 1 is carried to the left, and the 0 is written at the bottom of the rightmost column. The second column from the right is added:1 + 0 + 1 = 10₂again; the 1 is carried, and 0 is written at the bottom. The third column:1 + 1 + 1 = 11₂.This time, a 1 is carried, and a 1 is written in the bottom row. Proceeding like this gives the final answer 100100₂(36₁₀).

Computers

Addition with an op-amp. SeeSumming amplifierfor details.

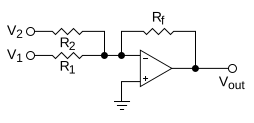
Analog computerswork directly with physical quantities, so their addition mechanisms depend on the form of the addends. A mechanical adder might represent two addends as the positions of sliding blocks, in which case they can be added with anaveraginglever.If the addends are the rotation speeds of twoshafts,they can be added with adifferential.A hydraulic adder can add thepressuresin two chambers by exploitingNewton's second lawto balance forces on an assembly ofpistons.The most common situation for a general-purpose analog computer is to add twovoltages(referenced toground); this can be accomplished roughly with aresistornetwork,but a better design exploits anoperational amplifier.

Addition is also fundamental to the operation ofdigital computers,where the efficiency of addition, in particular thecarrymechanism, is an important limitation to overall performance.

Part of Charles Babbage'sDifference Engineincluding the addition and carry mechanisms

Theabacus,also called a counting frame, is a calculating tool that was in use centuries before the adoption of the written modern numeral system and is still widely used by merchants, traders and clerks inAsia,Africa,and elsewhere; it dates back to at least 2700–2300 BC, when it was used inSumer.

Blaise Pascalinvented the mechanical calculator in 1642;it was the first operationaladding machine.It made use of a gravity-assisted carry mechanism. It was the only operational mechanical calculator in the 17th centuryand the earliest automatic, digital computer.Pascal's calculatorwas limited by its carry mechanism, which forced its wheels to only turn one way so it could add. To subtract, the operator had to use thePascal's calculator's complement,which required as many steps as an addition.Giovanni Polenifollowed Pascal, building the second functional mechanical calculator in 1709, a calculating clock made of wood that, once setup, could multiply two numbers automatically.

"Full adder"logic circuit that adds two binary digits,AandB,along with a carry inputC_in,producing the sum bit,S,and a carry output,C_out.

Addersexecute integer addition in electronic digital computers, usually usingbinary arithmetic.The simplest architecture is the ripple carry adder, which follows the standard multi-digit algorithm. One slight improvement is thecarry skipdesign, again following human intuition; one does not perform all the carries in computing999 + 1,but one bypasses the group of 9s and skips to the answer.

In practice, computational addition may be achieved viaXORandANDbitwise logical operations in conjunction with bitshift operations as shown in the pseudocode below. Both XOR and AND gates are straightforward to realize in digital logic allowing the realization offull addercircuits which in turn may be combined into more complex logical operations. In modern digital computers, integer addition is typically the fastest arithmetic instruction, yet it has the largest impact on performance, since it underlies allfloating-point operationsas well as such basic tasks asaddressgeneration duringmemoryaccess and fetchinginstructionsduringbranching.To increase speed, modern designs calculate digits inparallel;these schemes go by such names as carry select,carry lookahead,and theLingpseudocarry. Many implementations are, in fact, hybrids of these last three designs.Unlike addition on paper, addition on a computer often changes the addends. On the ancientabacusand adding board, both addends are destroyed, leaving only the sum. The influence of the abacus on mathematical thinking was strong enough that earlyLatintexts often claimed that in the process of adding "a number to a number", both numbers vanish.In modern times, the ADD instruction of amicroprocessoroften replaces the augend with the sum but preserves the addend.In ahigh-level programming language,evaluatinga+bdoes not change eitheraorb;if the goal is to replaceawith the sum this must be explicitly requested, typically with the statementa=a+b.Some languages such asCorC++allow this to be abbreviated asa+=b.

// Iterative algorithm
intadd(intx,inty){
intcarry=0;
while(y!=0){
carry=AND(x,y);// Logical AND
x=XOR(x,y);// Logical XOR
y=carry<<1;// left bitshift carry by one
}
returnx;
}

// Recursive algorithm
intadd(intx,inty){
returnxif(y==0)elseadd(XOR(x,y),AND(x,y)<<1);
}

On a computer, if the result of an addition is too large to store, anarithmetic overflowoccurs, resulting in an incorrect answer. Unanticipated arithmetic overflow is a fairly common cause ofprogram errors.Such overflow bugs may be hard to discover and diagnose because they may manifest themselves only for very large input data sets, which are less likely to be used in validation tests.TheYear 2000 problemwas a series of bugs where overflow errors occurred due to use of a 2-digit format for years.

Addition of numbers

To prove the usual properties of addition, one must first define addition for the context in question. Addition is first defined on thenatural numbers.Inset theory,addition is then extended to progressively larger sets that include the natural numbers: theintegers,therational numbers,and thereal numbers.(Inmathematics education,positive fractions are added before negative numbers are even considered; this is also the historical route.)

Natural numbers

Further information:Natural number

There are two popular ways to define the sum of two natural numbersaandb.If one defines natural numbers to be thecardinalitiesof finite sets, (the cardinality of a set is the number of elements in the set), then it is appropriate to define their sum as follows:

• Let N(S) be the cardinality of a setS.Take two disjoint setsAandB,withN(A) =aandN(B) =b.Thena+bis defined as$N(A\cup B)$.

Here,A∪Bis theunionofAandB.An alternate version of this definition allowsAandBto possibly overlap and then takes theirdisjoint union,a mechanism that allows common elements to be separated out and therefore counted twice.

The other popular definition is recursive:

• Letn⁺be the successor ofn,that is the number followingnin the natural numbers, so0⁺= 1,1⁺= 2.Definea+ 0 =a.Define the general sum recursively bya+ (b⁺) = (a+b)⁺.Hence1 + 1 = 1 + 0⁺= (1 + 0)⁺=1⁺= 2.

Again, there are minor variations upon this definition in the literature. Taken literally, the above definition is an application of therecursion theoremon thepartially ordered setN².On the other hand, some sources prefer to use a restricted recursion theorem that applies only to the set of natural numbers. One then considersato be temporarily "fixed", applies recursion onbto define a function "a+ ", and pastes these unary operations for allatogether to form the full binary operation.

This recursive formulation of addition was developed by Dedekind as early as 1854, and he would expand upon it in the following decades.He proved the associative and commutative properties, among others, throughmathematical induction.

Integers

Further information:Integer

The simplest conception of an integer is that it consists of anabsolute value(which is a natural number) and asign(generally eitherpositiveornegative). The integer zero is a special third case, being neither positive nor negative. The corresponding definition of addition must proceed by cases:

• For an integern,let |n| be its absolute value. Letaandbbe integers. If eitheraorbis zero, treat it as an identity. Ifaandbare both positive, definea+b= |a| + |b|.Ifaandbare both negative, definea+b= −(|a| + |b|).Ifaandbhave different signs, definea+bto be the difference between |a| and |b|, with the sign of the term whose absolute value is larger.As an example,−6 + 4 = −2;because −6 and 4 have different signs, their absolute values are subtracted, and since the absolute value of the negative term is larger, the answer is negative.

Although this definition can be useful for concrete problems, the number of cases to consider complicates proofs unnecessarily. So the following method is commonly used for defining integers. It is based on the remark that every integer is the difference of two natural integers and that two such differences,a–bandc–dare equal if and only ifa+d=b+c. So, one can define formally the integers as theequivalence classesofordered pairsof natural numbers under theequivalence relation

(a,b) ~ (c,d)if and only ifa+d=b+c.

The equivalence class of(a,b)contains either(a–b,0)ifa≥b,or(0,b–a)otherwise. Ifnis a natural number, one can denote+nthe equivalence class of(n,0),and by–nthe equivalence class of(0,n).This allows identifying the natural numbernwith the equivalence class+n.

Addition of ordered pairs is done component-wise:

$(a,b)+(c,d)=(a+c,b+d).$

A straightforward computation shows that the equivalence class of the result depends only on the equivalences classes of the summands, and thus that this defines an addition of equivalence classes, that is integers.Another straightforward computation shows that this addition is the same as the above case definition.

This way of defining integers as equivalence classes of pairs of natural numbers, can be used to embed into agroupany commutativesemigroupwithcancellation property.Here, the semigroup is formed by the natural numbers and the group is the additive group of integers. The rational numbers are constructed similarly, by taking as semigroup the nonzero integers with multiplication.

This construction has been also generalized under the name ofGrothendieck groupto the case of any commutative semigroup. Without the cancellation property thesemigroup homomorphismfrom the semigroup into the group may be non-injective. Originally, theGrothendieck groupwas, more specifically, the result of this construction applied to the equivalences classes under isomorphisms of the objects of anabelian category,with thedirect sumas semigroup operation.

Rational numbers (fractions)

Addition ofrational numberscan be computed using theleast common denominator,but a conceptually simpler definition involves only integer addition and multiplication:

• Define${\frac {a}{b}}+{\frac {c}{d}}={\frac {ad+bc}{bd}}.$

As an example, the sum${\frac {3}{4}}+{\frac {1}{8}}={\frac {3\times 8+4\times 1}{4\times 8}}={\frac {24+4}{32}}={\frac {28}{32}}={\frac {7}{8}}$.

Addition of fractions is much simpler when thedenominatorsare the same; in this case, one can simply add the numerators while leaving the denominator the same:${\frac {a}{c}}+{\frac {b}{c}}={\frac {a+b}{c}}$,so${\frac {1}{4}}+{\frac {2}{4}}={\frac {1+2}{4}}={\frac {3}{4}}$.

The commutativity and associativity of rational addition is an easy consequence of the laws of integer arithmetic.For a more rigorous and general discussion, seefield of fractions.

Real numbers

Further information:Construction of the real numbers

A common construction of the set of real numbers is the Dedekind completion of the set of rational numbers. A real number is defined to be aDedekind cutof rationals: anon-empty setof rationals that is closed downward and has nogreatest element.The sum of real numbersaandbis defined element by element:

• Define$a+b=\{q+r\mid q\in a,r\in b\}.$

This definition was first published, in a slightly modified form, byRichard Dedekindin 1872. The commutativity and associativity of real addition are immediate; defining the real number 0 to be the set of negative rationals, it is easily seen to be the additive identity. Probably the trickiest part of this construction pertaining to addition is the definition of additive inverses.

Adding π²/6 andeusing Cauchy sequences of rationals.

Unfortunately, dealing with multiplication of Dedekind cuts is a time-consuming case-by-case process similar to the addition of signed integers.Another approach is the metric completion of the rational numbers. A real number is essentially defined to be the limit of aCauchy sequenceof rationals, lima_n.Addition is defined term by term:

• Define$\lim _{n}a_{n}+\lim _{n}b_{n}=\lim _{n}(a_{n}+b_{n}).$

This definition was first published byGeorg Cantor,also in 1872, although his formalism was slightly different. One must prove that this operation is well-defined, dealing with co-Cauchy sequences. Once that task is done, all the properties of real addition follow immediately from the properties of rational numbers. Furthermore, the other arithmetic operations, including multiplication, have straightforward, analogous definitions.

Complex numbers

Addition of two complex numbers can be done geometrically by constructing a parallelogram.

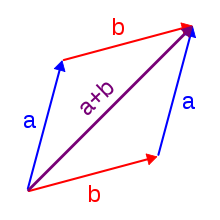
Complex numbers are added by adding the real and imaginary parts of the summands.That is to say:

$(a+bi)+(c+di)=(a+c)+(b+d)i.$

Using the visualization of complex numbers in the complex plane, the addition has the following geometric interpretation: the sum of two complex numbersAandB,interpreted as points of the complex plane, is the pointXobtained by building aparallelogramthree of whose vertices areO,AandB.Equivalently,Xis the point such that thetriangleswith verticesO,A,B,andX,B,A,arecongruent.

Generalizations

There are many binary operations that can be viewed as generalizations of the addition operation on the real numbers. The field ofabstract algebrais centrally concerned with such generalized operations, and they also appear inset theoryandcategory theory.

Abstract algebra

Vectors

Main article:Vector addition

Inlinear algebra,avector spaceis an algebraic structure that allows for adding any twovectorsand for scaling vectors. A familiar vector space is the set of all ordered pairs of real numbers; the ordered pair (a,b) is interpreted as a vector from the origin in the Euclidean plane to the point (a,b) in the plane. The sum of two vectors is obtained by adding their individual coordinates:

$(a,b)+(c,d)=(a+c,b+d).$

This addition operation is central toclassical mechanics,in whichvelocities,accelerationsandforcesare all represented by vectors.

Matrices

Main article:Matrix addition

Matrix addition is defined for two matrices of the same dimensions. The sum of twom×n(pronounced "m by n" ) matricesAandB,denoted byA+B,is again anm×nmatrix computed by adding corresponding elements:

${\begin{aligned}\mathbf {A} +\mathbf {B} &={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{bmatrix}}+{\begin{bmatrix}b_{11}&b_{12}&\cdots &b_{1n}\\b_{21}&b_{22}&\cdots &b_{2n}\\\vdots &\vdots &\ddots &\vdots \\b_{m1}&b_{m2}&\cdots &b_{mn}\\\end{bmatrix}}\\&={\begin{bmatrix}a_{11}+b_{11}&a_{12}+b_{12}&\cdots &a_{1n}+b_{1n}\\a_{21}+b_{21}&a_{22}+b_{22}&\cdots &a_{2n}+b_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}+b_{m1}&a_{m2}+b_{m2}&\cdots &a_{mn}+b_{mn}\\\end{bmatrix}}\\\end{aligned}}$

For example:

${\begin{bmatrix}1&3\\1&0\\1&2\end{bmatrix}}+{\begin{bmatrix}0&0\\7&5\\2&1\end{bmatrix}}={\begin{bmatrix}1+0&3+0\\1+7&0+5\\1+2&2+1\end{bmatrix}}={\begin{bmatrix}1&3\\8&5\\3&3\end{bmatrix}}$

Modular arithmetic

Main article:Modular arithmetic

Inmodular arithmetic,the set of available numbers is restricted to a finite subset of the integers, and addition "wraps around" when reaching a certain value, called the modulus. For example, the set of integers modulo 12 has twelve elements; it inherits an addition operation from the integers that is central tomusical set theory.The set of integers modulo 2 has just two elements; the addition operation it inherits is known inBoolean logicas the "exclusive or"function. A similar" wrap around "operation arises ingeometry,where the sum of twoangle measuresis often taken to be their sum as real numbers modulo 2π. This amounts to an addition operation on thecircle,which in turn generalizes to addition operations on many-dimensionaltori.

General theory

The general theory of abstract algebra allows an "addition" operation to be anyassociativeandcommutativeoperation on a set. Basicalgebraic structureswith such an addition operation includecommutative monoidsandabelian groups.

Set theory and category theory

A far-reaching generalization of addition of natural numbers is the addition ofordinal numbersandcardinal numbersin set theory. These give two different generalizations of addition of natural numbers to thetransfinite.Unlike most addition operations, addition of ordinal numbers is not commutative.Addition of cardinal numbers, however, is a commutative operation closely related to thedisjoint unionoperation.

Incategory theory,disjoint union is seen as a particular case of thecoproductoperation,and general coproducts are perhaps the most abstract of all the generalizations of addition. Some coproducts, such asdirect sumandwedge sum,are named to evoke their connection with addition.

Related operations

Addition, along with subtraction, multiplication and division, is considered one of the basic operations and is used inelementary arithmetic.

Arithmetic

Subtractioncan be thought of as a kind of addition—that is, the addition of anadditive inverse.Subtraction is itself a sort of inverse to addition, in that addingxand subtractingxareinverse functions.

Given a set with an addition operation, one cannot always define a corresponding subtraction operation on that set; the set of natural numbers is a simple example. On the other hand, a subtraction operation uniquely determines an addition operation, an additive inverse operation, and an additive identity; for this reason, an additive group can be described as a set that is closed under subtraction.

Multiplicationcan be thought of asrepeated addition.If a single termxappears in a sumntimes, then the sum is the product ofnandx.Ifnis not anatural number,the product may still make sense; for example, multiplication by−1yields theadditive inverseof a number.

A circular slide rule

In the real and complex numbers, addition and multiplication can be interchanged by theexponential function:

$e^{a+b}=e^{a}e^{b}.$

This identity allows multiplication to be carried out by consulting atableoflogarithmsand computing addition by hand; it also enables multiplication on aslide rule.The formula is still a good first-order approximation in the broad context ofLie groups,where it relates multiplication of infinitesimal group elements with addition of vectors in the associatedLie algebra.

There are even more generalizations of multiplication than addition.In general, multiplication operations alwaysdistributeover addition; this requirement is formalized in the definition of aring.In some contexts, such as the integers, distributivity over addition and the existence of a multiplicative identity is enough to uniquely determine the multiplication operation. The distributive property also provides information about addition; by expanding the product(1 + 1)(a+b)in both ways, one concludes that addition is forced to be commutative. For this reason, ring addition is commutative in general.

Divisionis an arithmetic operation remotely related to addition. Sincea/b=a(b⁻¹),division is right distributive over addition:(a+b) /c=a/c+b/c.However, division is not left distributive over addition;1 / (2 + 2)is not the same as1/2 + 1/2.

Ordering

Log-log plotofx+ 1andmax (x,1)fromx= 0.001 to 1000

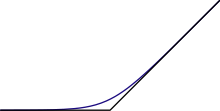
The maximum operation "max (a,b) "is a binary operation similar to addition. In fact, if two nonnegative numbersaandbare of differentorders of magnitude,then their sum is approximately equal to their maximum. This approximation is extremely useful in the applications of mathematics, for example in truncatingTaylor series.However, it presents a perpetual difficulty innumerical analysis,essentially since "max" is not invertible. Ifbis much greater thana,then a straightforward calculation of(a+b) −bcan accumulate an unacceptableround-off error,perhaps even returning zero. See alsoLoss of significance.

The approximation becomes exact in a kind of infinite limit; if eitheraorbis an infinitecardinal number,their cardinal sum is exactly equal to the greater of the two.Accordingly, there is no subtraction operation for infinite cardinals.

Maximization is commutative and associative, like addition. Furthermore, since addition preserves the ordering of real numbers, addition distributes over "max" in the same way that multiplication distributes over addition:

$a+\max(b,c)=\max(a+b,a+c).$

For these reasons, intropical geometryone replaces multiplication with addition and addition with maximization. In this context, addition is called "tropical multiplication", maximization is called "tropical addition", and the tropical "additive identity" isnegative infinity.Some authors prefer to replace addition with minimization; then the additive identity is positive infinity.

Tying these observations together, tropical addition is approximately related to regular addition through thelogarithm:

$\log(a+b)\approx \max(\log a,\log b),$

which becomes more accurate as the base of the logarithm increases.The approximation can be made exact by extracting a constanth,named by analogy with thePlanck constantfromquantum mechanics,and taking the "classical limit"ashtends to zero:

$\max(a,b)=\lim _{h\to 0}h\log(e^{a/h}+e^{b/h}).$

In this sense, the maximum operation is adequantizedversion of addition.

Other ways to add

Incrementation, also known as thesuccessor operation,is the addition of1to a number.

Summationdescribes the addition of arbitrarily many numbers, usually more than just two. It includes the idea of the sum of a single number, which is itself, and theempty sum,which iszero.An infinite summation is a delicate procedure known as aseries.

Countinga finite set is equivalent to summing 1 over the set.

Integrationis a kind of "summation" over acontinuum,or more precisely and generally, over adifferentiable manifold.Integration over a zero-dimensional manifold reduces to summation.

Linear combinationscombine multiplication and summation; they are sums in which each term has a multiplier, usually arealorcomplexnumber. Linear combinations are especially useful in contexts where straightforward addition would violate some normalization rule, such asmi xingofstrategiesingame theoryorsuperpositionofstatesinquantum mechanics.

Convolutionis used to add two independentrandom variablesdefined bydistribution functions.Its usual definition combines integration, subtraction, and multiplication.In general, convolution is useful as a kind of domain-side addition; by contrast, vector addition is a kind of range-side addition.

See also

• Lunar arithmetic
• Mental arithmetic
• Parallel addition (mathematics)
• Verbal arithmetic(also known as cryptarithms), puzzles involving addition

References

History

• Ferreirós, José (1999).Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics.Birkhäuser.ISBN978-0-8176-5749-9.
• Karpinski, Louis(1925).The History of Arithmetic.Rand McNally.LCCQA21.K3.
• Schwartzman, Steven (1994).The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English.MAA.ISBN978-0-88385-511-9.
• Williams, Michael (1985).A History of Computing Technology.Prentice-Hall.ISBN978-0-13-389917-7.

Elementary mathematics

• Sparks, F.; Rees C. (1979).A Survey of Basic Mathematics.McGraw-Hill.ISBN978-0-07-059902-4.

Education

• Begle, Edward (1975).The Mathematics of the Elementary School.McGraw-Hill.ISBN978-0-07-004325-1.
• California State Board of Education mathematics content standardsAdopted December 1997, accessed December 2005.
• Devine, D.; Olson, J.; Olson, M. (1991).Elementary Mathematics for Teachers(2e ed.).Wiley.ISBN978-0-471-85947-5.
• National Research Council(2001).Adding It Up: Helping Children Learn Mathematics.National Academy Press.doi:10.17226/9822.ISBN978-0-309-06995-3.
• Van de Walle, John (2004).Elementary and Middle School Mathematics: Teaching developmentally(5e ed.). Pearson.ISBN978-0-205-38689-5.

Cognitive science

• Fosnot, Catherine T.; Dolk, Maarten (2001).Young Mathematicians at Work: Constructing Number Sense, Addition, and Subtraction.Heinemann.ISBN978-0-325-00353-5.
• Wynn, Karen (1998). "Numerical competence in infants".The Development of Mathematical Skills.Taylor & Francis.ISBN0-86377-816-X.

Mathematical exposition

• Bogomolny, Alexander (1996)."Addition".Interactive Mathematics Miscellany and Puzzles (cut-the-knot.org).Archivedfrom the original on April 26, 2006.Retrieved3 February2006.
• Cheng, Eugenia(2017).Beyond Infinity: An Expedition to the Outer Limits of Mathematics.Basic Books.ISBN978-1-541-64413-7.
• Dunham, William (1994).The Mathematical Universe.Wiley.ISBN978-0-471-53656-7.
• Johnson, Paul (1975).From Sticks and Stones: Personal Adventures in Mathematics.Science Research Associates.ISBN978-0-574-19115-1.
• Linderholm, Carl (1971).Mathematics Made Difficult.Wolfe.ISBN978-0-7234-0415-6.
• Smith, Frank (2002).The Glass Wall: Why Mathematics Can Seem Difficult.Teachers College Press.ISBN978-0-8077-4242-6.
• Smith, Karl (1980).The Nature of Modern Mathematics(3rd ed.). Wadsworth.ISBN978-0-8185-0352-8.

Advanced mathematics

• Bergman, George (2005).An Invitation to General Algebra and Universal Constructions(2.3 ed.). General Printing.ISBN978-0-9655211-4-7.
• Burrill, Claude (1967).Foundations of Real Numbers.McGraw-Hill.LCCQA248.B95.
• Dummit, D.; Foote, R. (1999).Abstract Algebra(2 ed.). Wiley.ISBN978-0-471-36857-1.
• Gbur, Greg(2011).Mathematical Methods for Optical Physics and Engineering.Cambridge University Press.ISBN978-0-511-91510-9.OCLC704518582.
• Enderton, Herbert (1977).Elements of Set Theory.Academic Press.ISBN978-0-12-238440-0.
• Lee, John (2003).Introduction to Smooth Manifolds.Springer.ISBN978-0-387-95448-6.
• Martin, John (2003).Introduction to Languages and the Theory of Computation(3 ed.). McGraw-Hill.ISBN978-0-07-232200-2.
• Riehl, Emily(2016).Category Theory in Context.Dover.ISBN978-0-486-80903-8.
• Rudin, Walter (1976).Principles of Mathematical Analysis(3 ed.). McGraw-Hill.ISBN978-0-07-054235-8.
• Stewart, James (1999).Calculus: Early Transcendentals(4 ed.). Brooks/Cole.ISBN978-0-534-36298-0.

Mathematical research

• Akian, Marianne; Bapat, Ravindra; Gaubert, Stephane (2005). "Min-plus methods in eigenvalue perturbation theory and generalised Lidskii-Vishik-Ljusternik theorem".INRIA Reports.arXiv:math.SP/0402090.Bibcode:2004math......2090A.
• Baez, J.;Dolan, J. (2001).Mathematics Unlimited – 2001 and Beyond. From Finite Sets to Feynman Diagrams.p. 29.arXiv:math.QA/0004133.ISBN3-540-66913-2.
• Litvinov, Grigory; Maslov, Victor; Sobolevskii, Andreii (1999).Idempotent mathematics and interval analysis.Reliable Computing,Kluwer.
• Loday, Jean-Louis (2002). "Arithmetree".Journal of Algebra.258:275.arXiv:math/0112034.doi:10.1016/S0021-8693(02)00510-0.
• Mikhalkin, Grigory (2006). Sanz-Solé, Marta (ed.).Proceedings of the International Congress of Mathematicians (ICM), Madrid, Spain, August 22–30, 2006. Volume II: Invited lectures. Tropical Geometry and its Applications.Zürich:European Mathematical Society.pp. 827–852.arXiv:math.AG/0601041.ISBN978-3-03719-022-7.Zbl1103.14034.
• Viro, Oleg (2001). Cascuberta, Carles; Miró-Roig, Rosa Maria; Verdera, Joan; Xambó-Descamps, Sebastià (eds.).European Congress of Mathematics: Barcelona, July 10–14, 2000, Volume I. Dequantization of Real Algebraic Geometry on Logarithmic Paper.Progress in Mathematics. Vol. 201. Basel: Birkhäuser. pp. 135–146.arXiv:math/0005163.Bibcode:2000math......5163V.ISBN978-3-7643-6417-5.Zbl1024.14026.

Computing

• Flynn, M.; Oberman, S. (2001).Advanced Computer Arithmetic Design.Wiley.ISBN978-0-471-41209-0.
• Horowitz, P.; Hill, W. (2001).The Art of Electronics(2 ed.). Cambridge UP.ISBN978-0-521-37095-0.
• Jackson, Albert (1960).Analog Computation.McGraw-Hill.LCCQA76.4 J3.
• Rieffel, Eleanor G.;Polak, Wolfgang H. (4 March 2011).Quantum Computing: A Gentle Introduction.MIT Press.ISBN978-0-262-01506-6.
• Truitt, T.; Rogers, A. (1960).Basics of Analog Computers.John F. Rider.LCCQA76.4 T7.
• Marguin, Jean (1994).Histoire des Instruments et Machines à Calculer, Trois Siècles de Mécanique Pensante 1642–1942(in French). Hermann.ISBN978-2-7056-6166-3.
• Taton, René (1963).Le Calcul Mécanique. Que Sais-Je? n° 367(in French). Presses universitaires de France. pp. 20–28.

Further reading

• Baroody, Arthur; Tiilikainen, Sirpa (2003).The Development of Arithmetic Concepts and Skills. Two perspectives on addition development.Routledge. p.75.ISBN0-8058-3155-X.
• Davison, David M.; Landau, Marsha S.; McCracken, Leah; Thompson, Linda (1999).Mathematics: Explorations & Applications(TE ed.). Prentice Hall.ISBN978-0-13-435817-8.
• Bunt, Lucas N.H.; Jones, Phillip S.; Bedient, Jack D. (1976).The Historical roots of Elementary Mathematics.Prentice-Hall.ISBN978-0-13-389015-0.
• Poonen, Bjorn (2010)."Addition".Girls' Angle Bulletin.3(3–5).ISSN2151-5743.
• Weaver, J. Fred (1982). "Addition and Subtraction: A Cognitive Perspective".Addition and Subtraction: A Cognitive Perspective. Interpretations of Number Operations and Symbolic Representations of Addition and Subtraction.Taylor & Francis. p. 60.ISBN0-89859-171-6.