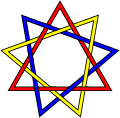
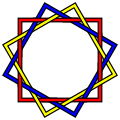
Brunnian link

This four-component link is a Brunnian link.

Inknot theory,a branch oftopology,aBrunnian linkis a nontriviallinkthat becomes a set of trivialunlinkedcircles if any one component is removed. In other words, cutting any loop frees all the other loops (so that no two loops can bedirectly linked).

The nameBrunnianis afterHermann Brunn.Brunn's 1892 articleÜber Verkettungincluded examples of such links.

Examples

TheBorromean ringsare the simplest Brunnian link.

Six-component "rubberband" Brunnian link. The same construction leads to Brunnian links with arbitrary numbers of components.

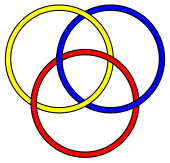
The best-known and simplest possible Brunnian link is theBorromean rings,a link of threeunknots.However for every number three or above, there are an infinite number of links with the Brunnian property containing that number of loops. Here are some relatively simple three-component Brunnian links which are not the same as the Borromean rings:

• 
  12-crossing link.
• 
  18-crossing link.
• 
  24-crossing link.

The simplest Brunnian link other than the 6-crossing Borromean rings is presumably the 10-crossingL10a140 link.

An example of ann-component Brunnian link is given by the "rubberband" Brunnian Links, where each component is looped around the next asaba⁻¹b⁻¹,with the last looping around the first, forming a circle.

In 2020, new and much more complicated Brunnian links were discovered inusing highly flexible geometric-topology methods. See Section 6.

Non-circularity

It is impossible for a Brunnian link to be constructed from geometric circles. Somewhat more generally, if a link has the property that each component is a circle and no two components are linked, then it is trivial. The proof, byMichael Freedmanand Richard Skora, embeds the three-dimensional space containing the link as the boundary of aPoincaré ball modelof four-dimensionalhyperbolic space,and considers the hyperbolicconvex hullsof the circles. These are two-dimensional subspaces of the hyperbolic space, and their intersection patterns reflect the pairwise linking of the circles: if two circles are linked, then their hulls have a point of intersection, but with the assumption that pairs of circles are unlinked, the hulls are disjoint. Taking cross-sections of the Poincaré ball by concentric three-dimensional spheres, the intersection of each sphere with the hulls of the circles is again a link made out of circles, and this family of cross-sections provides a continuous motion of all of the circles that shrinks each of them to a point without crossing any of the others.

Classification

Brunnian links were classified up tolink-homotopybyJohn Milnorin (Milnor 1954), and the invariants he introduced are now calledMilnor invariants.

An (n+ 1)-component Brunnian link can be thought of as an element of thelink group– which in this case (but not in general) is thefundamental groupof thelink complement– of then-component unlink, since by Brunnianness removing the last link unlinks the others. The link group of then-component unlink is thefree grouponngenerators,F_n,as the link group of a single link is theknot groupof theunknot,which is the integers, and the link group of an unlinked union is thefree productof the link groups of the components.

Not every element of the link group gives a Brunnian link, as removing anyothercomponent must also unlink the remainingnelements. Milnor showed that the group elements that do correspond to Brunnian links are related to thegraded Lie algebraof thelower central seriesof the free group, which can be interpreted as "relations" in thefree Lie algebra.

In 2021, two special satellite operations were investigated for Brunnian links in 3-sphere, called "satellite-sum" and "satellite-tie", both of which can be used to construct infinitely many distinct Brunnian links from almost every Brunnian link.A geometric classification theorem for Brunnian links was given.More interestingly, a canonical geometric decomposition in terms of satellite-sum and satellite-tie, which is simpler than JSJ-decomposition, for Brunnian links, was developed. The building blocks of Brunnian links therein turn out to be Hopf -links, hyperbolic Brunnian links, and hyperbolic Brunnian links in unlink-complements, the last of which can be further reduced into a Brunnian link in 3-sphere.

Massey products

Main article:Massey product

Brunnian links can be understood inalgebraic topologyviaMassey products:a Massey product is ann-fold product which is only defined if all (n− 1)-fold products of its terms vanish. This corresponds to the Brunnian property of all (n− 1)-component sublinks being unlinked, but the overalln-component link being non-trivially linked.

Brunnian braids

See also:Closed braid

The standard braid is Brunnian: if one removes the black strand, the blue strand is always on top of the red strand, and they are thus not braided around each other; likewise for removing other strands.

A Brunnianbraidis a braid that becomes trivial upon removal of any one of its strings. Brunnian braids form asubgroupof thebraid group.Brunnian braids over the 2-spherethat are not Brunnian over the 2-diskgive rise to non-trivial elements in the homotopy groups of the 2-sphere. For example, the "standard" braid corresponding to the Borromean rings gives rise to theHopf fibrationS³→S²,and iteration of this (as in everyday braiding) is likewise Brunnian.

Real-world examples

Rainbow loom bracelet showing Brunnian chains

Manydisentanglement puzzlesand somemechanical puzzlesare variants of Brunnian Links, with the goal being to free a single piece only partially linked to the rest, thus dismantling the structure.

Brunnian chains are also used to create wearable and decorative items out of elastic bands using devices such as theRainbow LoomorWonder Loom.

Further reading

• Berrick, A. Jon; Cohen, Frederick R.; Wong, Yan Loi; Wu, Jie (2006),"Configurations, braids, and homotopy groups",Journal of the American Mathematical Society,19(2): 265–326,doi:10.1090/S0894-0347-05-00507-2,MR2188127.
• Hermann Brunn, "Über Verkettung", J. Münch. Ber, XXII. 77–99 (1892).JFM24.0507.01(in German)
• Milnor, John(March 1954), "Link Groups",Annals of Mathematics,59(2), Annals of Mathematics: 177–195,doi:10.2307/1969685,JSTOR1969685
• Rolfsen, Dale (1976),Knots and Links,Mathematics Lecture Series, vol. 7,Berkeley, California:Publish or Perish,ISBN0-914098-16-0,MR0515288

External links

• "Are Borromean Links so Rare?", by Slavik Jablan(also available in its original form as published in the journalFormahere (PDF file)Archived2021-02-28 at theWayback Machine).
• "Brunnian_link",The Knot Atlas.