Catenary

This article is about the mathematical curve. For other uses, seeCatenary (disambiguation).

"Chainette" redirects here. For the wine grape also known as Chainette, seeCinsaut.

Achainhanging from points forms a catenary.

Freely-hangingoverhead power linesalso form a catenary (most prominently visible with high-voltage lines, and with some imperfection near to theinsulators).

The silk on aspider's webforming multipleelasticcatenaries.

Inphysicsandgeometry,acatenary(US:/ˈkætənɛri/KAT-ən-err-ee,UK:/kəˈtiːnəri/kə-TEE-nər-ee) is thecurvethat an idealized hangingchainorcableassumes under its ownweightwhen supported only at its ends in a uniform gravitational field.

The catenary curve has a U-like shape, superficially similar in appearance to aparabola,which it is not.

The curve appears in the design of certain types ofarchesand as a cross section of thecatenoid—the shape assumed by a soap film bounded by two parallel circular rings.

The catenary is also called thealysoid,chainette,or, particularly in the materials sciences, an example of afunicular.Rope staticsdescribes catenaries in a classic statics problem involving a hanging rope.

Mathematically, the catenary curve is thegraphof thehyperbolic cosinefunction. Thesurface of revolutionof the catenary curve, thecatenoid,is aminimal surface,specifically aminimal surface of revolution.A hanging chain will assume a shape of least potential energy which is a catenary.Galileo Galileiin 1638 discussed the catenary in the bookTwo New Sciencesrecognizing that it was different from aparabola.The mathematical properties of the catenary curve were studied byRobert Hookein the 1670s, and its equation was derived byLeibniz,HuygensandJohann Bernoulliin 1691.

Catenaries and related curves are used in architecture and engineering (e.g., in the design of bridges andarchesso that forces do not result in bending moments). In the offshore oil and gas industry, "catenary" refers to asteel catenary riser,a pipeline suspended between a production platform and the seabed that adopts an approximate catenary shape. In the rail industry it refers to theoverhead wiringthat transfers power to trains. (This often supports a contact wire, in which case it does not follow a true catenary curve.)

In optics and electromagnetics, the hyperbolic cosine and sine functions are basic solutions to Maxwell's equations.The symmetric modes consisting of twoevanescent waveswould form a catenary shape.

History

Antoni Gaudí's catenary model atCasa Milà

The word "catenary" is derived from the Latin wordcatēna,which means "chain".The English word" catenary "is usually attributed toThomas Jefferson, who wrote in a letter toThomas Paineon the construction of an arch for a bridge:

I have lately received from Italy a treatise on theequilibriumof arches, by the Abbé Mascheroni. It appears to be a very scientifical work. I have not yet had time to engage in it; but I find that the conclusions of his demonstrations are, that every part of the catenary is in perfect equilibrium.

It is often saidthatGalileothought the curve of a hanging chain was parabolic. However, in hisTwo New Sciences(1638), Galileo wrote that a hanging cord is only an approximate parabola, correctly observing that this approximation improves in accuracy as the curvature gets smaller and is almost exact when the elevation is less than 45°.The fact that the curve followed by a chain is not a parabola was proven byJoachim Jungius(1587–1657); this result was published posthumously in 1669.

The application of the catenary to the construction of arches is attributed toRobert Hooke,whose "true mathematical and mechanical form" in the context of the rebuilding ofSt Paul's Cathedralalluded to a catenary.Some much older arches approximate catenaries, an example of which is the Arch ofTaq-i KisrainCtesiphon.

Analogy between an arch and a hanging chain and comparison to the dome ofSaint Peter's Basilicain Rome (Giovanni Poleni,1748)

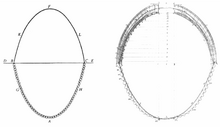
In 1671, Hooke announced to theRoyal Societythat he had solved the problem of the optimal shape of an arch, and in 1675 published an encrypted solution as a Latinanagramin an appendix to hisDescription of Helioscopes,where he wrote that he had found "a true mathematical and mechanical form of all manner of Arches for Building." He did not publish the solution to this anagramin his lifetime, but in 1705 his executor provided it asut pendet continuum flexile, sic stabit contiguum rigidum inversum,meaning "As hangs a flexible cable so, inverted, stand the touching pieces of an arch."

In 1691,Gottfried Leibniz,Christiaan Huygens,andJohann Bernoulliderived theequationin response to a challenge byJakob Bernoulli;their solutions were published in theActa Eruditorumfor June 1691.David Gregorywrote a treatise on the catenary in 1697in which he provided an incorrect derivation of the correct differential equation.

Eulerproved in 1744 that the catenary is the curve which, when rotated about thex-axis, gives the surface of minimumsurface area(thecatenoid) for the given bounding circles.Nicolas Fussgave equations describing the equilibrium of a chain under anyforcein 1796.

Inverted catenary arch

Catenary archesare often used in the construction ofkilns.To create the desired curve, the shape of a hanging chain of the desired dimensions is transferred to a form which is then used as a guide for the placement of bricks or other building material.

TheGateway ArchinSt. Louis, Missouri,United States is sometimes said to be an (inverted) catenary, but this is incorrect.It is close to a more general curve called a flattened catenary, with equationy=A cosh(Bx),which is a catenary ifAB= 1.While a catenary is the ideal shape for a freestanding arch of constant thickness, the Gateway Arch is narrower near the top. According to the U.S.National Historic Landmarknomination for the arch, it is a "weighted catenary"instead. Its shape corresponds to the shape that a weighted chain, having lighter links in the middle, would form.

• 
  Catenaryarches under the roof ofGaudí'sCasa Milà,Barcelona,Spain.
• 
  TheSheffield Winter Gardenis enclosed by a series ofcatenary arches.
• 
  TheGateway Arch(St. Louis, Missouri) is a flattened catenary.
• 
  Catenary arch kiln under construction over temporary form

Catenary bridges

Simple suspension bridgesare essentially thickened cables, and follow a catenary curve.

Stressed ribbon bridges,like theLeonel Viera BridgeinMaldonado, Uruguay,also follow a catenary curve, with cables embedded in a rigid deck.

In free-hanging chains, the force exerted is uniform with respect to length of the chain, and so the chain follows the catenary curve.The same is true of asimple suspension bridgeor "catenary bridge," where the roadway follows the cable.

Astressed ribbon bridgeis a more sophisticated structure with the same catenary shape.

However, in asuspension bridgewith a suspended roadway, the chains or cables support the weight of the bridge, and so do not hang freely. In most cases the roadway is flat, so when the weight of the cable is negligible compared with the weight being supported, the force exerted is uniform with respect to horizontal distance, and the result is aparabola,as discussed below (although the term "catenary" is often still used, in an informal sense). If the cable is heavy then the resulting curve is between a catenary and a parabola.

Comparison of acatenary arch(black dotted curve) and aparabolic arch(red solid curve) with the same span and sag. The catenary represents the profile of a simple suspension bridge, or the cable of a suspended-deck suspension bridge on which its deck and hangers have negligible weight compared to its cable. The parabola represents the profile of the cable of a suspended-deck suspension bridge on which its cable and hangers have negligible weight compared to its deck. The profile of the cable of a real suspension bridge with the same span and sag lies between the two curves. The catenary and parabola equations are respectively,$y={\text{cosh }}x$and$y=x^{2}[({\text{cosh }}1)-1]+1$

Anchoring of marine objects

A heavyanchorchain forms a catenary, with a low angle of pull on the anchor.

The catenary produced by gravity provides an advantage to heavyanchor rodes.An anchor rode (or anchor line) usually consists of chain or cable or both. Anchor rodes are used by ships, oil rigs, docks,floating wind turbines,and other marine equipment which must be anchored to the seabed.

When the rope is slack, the catenary curve presents a lower angle of pull on theanchoror mooring device than would be the case if it were nearly straight. This enhances the performance of the anchor and raises the level of force it will resist before dragging. To maintain the catenary shape in the presence of wind, a heavy chain is needed, so that only larger ships in deeper water can rely on this effect. Smaller boats also rely on catenary to maintain maximum holding power.

Cable ferriesandchain boatspresent a special case of marine vehicles moving although moored by the two catenaries each of one or more cables (wire ropes or chains) passing through the vehicle and moved along by motorized sheaves. The catenaries can be evaluated graphically.

Mathematical description

Equation

Catenaries for different values ofa

The equation of a catenary inCartesian coordinateshas the form

$$y=a\cosh \left({\frac {x}{a}}\right)={\frac {a}{2}}\left(e^{\frac {x}{a}}+e^{-{\frac {x}{a}}}\right),$$ wherecoshis thehyperbolic cosine function,and whereais the distance of the lowest point above the x axis.All catenary curves aresimilarto each other, since changing the parameterais equivalent to auniform scalingof the curve.

TheWhewell equationfor the catenary is $$\tan \varphi ={\frac {s}{a}},$$ where$\varphi$is thetangential angleandsthearc length.

Differentiating gives $${\frac {d\varphi }{ds}}={\frac {\cos ^{2}\varphi }{a}},$$ and eliminating$\varphi$gives theCesàro equation $$\kappa ={\frac {a}{s^{2}+a^{2}}},$$ where$\kappa$is thecurvature.

Theradius of curvatureis then $$\rho =a\sec ^{2}\varphi,$$ which is the length of thenormalbetween the curve and thex-axis.

Relation to other curves

When aparabolais rolled along a straight line, theroulettecurve traced by itsfocusis a catenary.Theenvelopeof thedirectrixof the parabola is also a catenary.Theinvolutefrom the vertex, that is the roulette traced by a point starting at the vertex when a line is rolled on a catenary, is thetractrix.

Another roulette, formed by rolling a line on a catenary, is another line. This implies thatsquare wheelscan roll perfectly smoothly on a road made of a series of bumps in the shape of an inverted catenary curve. The wheels can be anyregular polygonexcept a triangle, but the catenary must have parameters corresponding to the shape and dimensions of the wheels.

Geometrical properties

Over any horizontal interval, the ratio of the area under the catenary to its length equalsa,independent of the interval selected. The catenary is the only plane curve other than a horizontal line with this property. Also, the geometric centroid of the area under a stretch of catenary is the midpoint of the perpendicular segment connecting the centroid of the curve itself and thex-axis.

Science

A movingchargein a uniformelectric fieldtravels along a catenary (which tends to aparabolaif the charge velocity is much less than thespeed of lightc).

Thesurface of revolutionwith fixed radii at either end that has minimum surface area is a catenary revolved about thex-axis.

Analysis

Model of chains and arches

In themathematical modelthe chain (or cord, cable, rope, string, etc.) is idealized by assuming that it is so thin that it can be regarded as acurveand that it is so flexible any force oftensionexerted by the chain is parallel to the chain.The analysis of the curve for an optimal arch is similar except that the forces of tension become forces ofcompressionand everything is inverted. An underlying principle is that the chain may be considered a rigid body once it has attained equilibrium.Equations which define the shape of the curve and the tension of the chain at each point may be derived by a careful inspection of the various forces acting on a segment using the fact that these forces must be in balance if the chain is instatic equilibrium.

Let the path followed by the chain be givenparametricallybyr= (x,y) = (x(s),y(s))wheresrepresentsarc lengthandris theposition vector.This is thenatural parameterizationand has the property that

$${\frac {d\mathbf {r} }{ds}}=\mathbf {u}$$

whereuis aunit tangent vector.

Diagram of forces acting on a segment of a catenary fromctor.The forces are the tensionT₀atc,the tensionTatr,and the weight of the chain(0, −ws).Since the chain is at rest the sum of these forces must be zero.

Adifferential equationfor the curve may be derived as follows.Letcbe the lowest point on the chain, called the vertex of the catenary.The slope⁠dy/dx⁠of the curve is zero atcsince it is a minimum point. Assumeris to the right ofcsince the other case is implied by symmetry. The forces acting on the section of the chain fromctorare the tension of the chain atc,the tension of the chain atr,and the weight of the chain. The tension atcis tangent to the curve atcand is therefore horizontal without any vertical component and it pulls the section to the left so it may be written(−T₀,0)whereT₀is the magnitude of the force. The tension atris parallel to the curve atrand pulls the section to the right. The tension atrcan be split into two components so it may be writtenTu= (Tcosφ,Tsinφ),whereTis the magnitude of the force andφis the angle between the curve atrand thex-axis (seetangential angle). Finally, the weight of the chain is represented by(0, −ws)wherewis the weight per unit length andsis the length of the segment of chain betweencandr.

The chain is in equilibrium so the sum of three forces is0,therefore

$$T\cos \varphi =T_{0}$$ and $$T\sin \varphi =ws\,,$$

and dividing these gives

$${\frac {dy}{dx}}=\tan \varphi ={\frac {ws}{T_{0}}}\,.$$

It is convenient to write

$$a={\frac {T_{0}}{w}}$$

which is the length of chain whose weight is equal in magnitude to the tension atc.Then

$${\frac {dy}{dx}}={\frac {s}{a}}$$

is an equation defining the curve.

The horizontal component of the tension,Tcosφ=T₀is constant and the vertical component of the tension,Tsinφ=wsis proportional to the length of chain betweenrand the vertex.

Derivation of equations for the curve

The differential equation$dy/dx=s/a$,given above, can be solved to produce equations for the curve. We will solve the equation using the boundary condition that the vertex is positioned at$s_{0}=0$and$(x,y)=(x_{0},y_{0})$.

First, invoke the formula for arc length to get $${\frac {ds}{dx}}={\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}={\sqrt {1+\left({\frac {s}{a}}\right)^{2}}}\,,$$ thenseparate variables to obtain $${\frac {ds}{\sqrt {1+(s/a)^{2}}}}=dx\,.$$

A reasonably straightforward approach to integrate this is to use hyperbolic substitution, which gives $$a\sinh ^{-1}{\frac {s}{a}}+x_{0}=x$$ (where$x_{0}$is aconstant of integration), and hence $${\frac {s}{a}}=\sinh {\frac {x-x_{0}}{a}}\,.$$

But${\textstyle s/a=dy/dx}$,so $${\frac {dy}{dx}}=\sinh {\frac {x-x_{0}}{a}}\,,$$ whichintegrates as $$y=a\cosh {\frac {x-x_{0}}{a}}+\delta$$ (with$\delta =y_{0}-a$being the constant of integration satisfying the boundary condition).

Since the primary interest here is simply the shape of the curve, the placement of the coordinate axes are arbitrary; so make the convenient choice of${\textstyle x_{0}=0=\delta }$ to simplify the result to $$y=a\cosh {\frac {x}{a}}\quad \square$$

For completeness, the$y\leftrightarrow s$relation can be derived by solving each of the$x\leftrightarrow y$and$x\leftrightarrow s$relations for$x/a$,giving: $$\cosh ^{-1}{\frac {y-\delta }{a}}={\frac {x-x_{0}}{a}}=\sinh ^{-1}{\frac {s}{a}}\,,$$ so $$y-\delta =a\cosh \left(\sinh ^{-1}{\frac {s}{a}}\right)\,,$$ whichcan be rewrittenas $$y-\delta =a{\sqrt {1+\left({\frac {s}{a}}\right)^{2}}}={\sqrt {a^{2}+s^{2}}}\,.$$

Alternative derivation

The differential equation can be solved using a different approach.From

$$s=a\tan \varphi$$

it follows that

$${\frac {dx}{d\varphi }}={\frac {dx}{ds}}{\frac {ds}{d\varphi }}=\cos \varphi \cdot a\sec ^{2}\varphi =a\sec \varphi$$ and $${\frac {dy}{d\varphi }}={\frac {dy}{ds}}{\frac {ds}{d\varphi }}=\sin \varphi \cdot a\sec ^{2}\varphi =a\tan \varphi \sec \varphi \,.$$

Integrating gives,

$$x=a\ln(\sec \varphi +\tan \varphi )+\ Alpha$$ and $$y=a\sec \varphi +\beta \,.$$

As before, thexandy-axes can be shifted soαandβcan be taken to be 0. Then

$$\sec \varphi +\tan \varphi =e^{\frac {x}{a}}\,,$$ and taking the reciprocal of both sides $$\sec \varphi -\tan \varphi =e^{-{\frac {x}{a}}}\,.$$

Adding and subtracting the last two equations then gives the solution $$y=a\sec \varphi =a\cosh \left({\frac {x}{a}}\right)\,,$$ and $$s=a\tan \varphi =a\sinh \left({\frac {x}{a}}\right)\,.$$

Determining parameters

Three catenaries through the same two points, depending on the horizontal forceT_H.

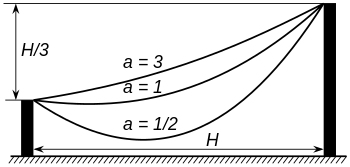
In general the parameterais the position of the axis. The equation can be determined in this case as follows:

Relabel if necessary so thatP₁is to the left ofP₂and letHbe the horizontal andvbe the vertical distance fromP₁toP₂.Translatethe axes so that the vertex of the catenary lies on they-axis and its heightais adjusted so the catenary satisfies the standard equation of the curve

$$y=a\cosh \left({\frac {x}{a}}\right)$$

and let the coordinates ofP₁andP₂be(x₁,y₁)and(x₂,y₂)respectively. The curve passes through these points, so the difference of height is

$$v=a\cosh \left({\frac {x_{2}}{a}}\right)-a\cosh \left({\frac {x_{1}}{a}}\right)\,.$$

and the length of the curve fromP₁toP₂is

$$L=a\sinh \left({\frac {x_{2}}{a}}\right)-a\sinh \left({\frac {x_{1}}{a}}\right)\,.$$

WhenL²−v²is expanded using these expressions the result is

$$L^{2}-v^{2}=2a^{2}\left(\cosh \left({\frac {x_{2}-x_{1}}{a}}\right)-1\right)=4a^{2}\sinh ^{2}\left({\frac {H}{2a}}\right)\,,$$ so $${\frac {1}{H}}{\sqrt {L^{2}-v^{2}}}={\frac {2a}{H}}\sinh \left({\frac {H}{2a}}\right)\,.$$

This is a transcendental equation inaand must be solvednumerically.Since$\sinh(x)/x$is strictly monotonic on$x>0$,there is at most one solution witha> 0and so there is at most one position of equilibrium.

However, if both ends of the curve (P₁andP₂) are at the same level (y₁=y₂), it can be shown that $$a={\frac {{\frac {1}{4}}L^{2}-h^{2}}{2h}}\,$$ where L is the total length of the curve betweenP₁andP₂andhis the sag (vertical distance betweenP₁,P₂and the vertex of the curve).

It can also be shown that $$L=2a\sinh {\frac {H}{2a}}\,$$ and $$H=2a\operatorname {arcosh} {\frac {h+a}{a}}\,$$ where H is the horizontal distance betweenP₁andP₂which are located at the same level (H=x₂−x₁).

The horizontal traction force atP₁andP₂isT₀=wa,wherewis the weight per unit length of the chain or cable.

Tension relations

There is a simple relationship between the tension in the cable at a point and itsx- and/ory- coordinate. Begin by combining the squares of the vector components of the tension: $$(T\cos \varphi )^{2}+(T\sin \varphi )^{2}=T_{0}^{2}+(ws)^{2}$$ which (recalling that$T_{0}=wa$) can be rewritten as $${\begin{aligned}T^{2}(\cos ^{2}\varphi +\sin ^{2}\varphi )&=(wa)^{2}+(ws)^{2}\\[6pt]T^{2}&=w^{2}(a^{2}+s^{2})\\[6pt]T&=w{\sqrt {a^{2}+s^{2}}}\,.\end{aligned}}$$ But,as shown above, $y={\sqrt {a^{2}+s^{2}}}$(assuming that$y_{0}=a$), so we get the simple relations $$T=wy=wa\cosh {\frac {x}{a}}\,.$$

Variational formulation

Consider a chain of length$L$suspended from two points of equal height and at distance$D$.The curve has to minimize its potential energy $$U=\int _{0}^{D}wy{\sqrt {1+y'^{2}}}dx$$ (wherewis the weight per unit length) and is subject to the constraint $$\int _{0}^{D}{\sqrt {1+y'^{2}}}dx=L\,.$$

The modifiedLagrangianis therefore $${\mathcal {L}}=(wy-\lambda ){\sqrt {1+y'^{2}}}$$ where$\lambda$is theLagrange multiplierto be determined. As the independent variable$x$does not appear in the Lagrangian, we can use theBeltrami identity $${\mathcal {L}}-y'{\frac {\partial {\mathcal {L}}}{\partial y'}}=C$$ where$C$is an integration constant, in order to obtain a first integral $${\frac {(wy-\lambda )}{\sqrt {1+y'^{2}}}}=-C$$

This is an ordinary first order differential equation that can be solved by the method ofseparation of variables.Its solution is the usual hyperbolic cosine where the parameters are obtained from the constraints.

Generalizations with vertical force

Nonuniform chains

If the density of the chain is variable then the analysis above can be adapted to produce equations for the curve given the density, or given the curve to find the density.

Letwdenote the weight per unit length of the chain, then the weight of the chain has magnitude

$$\int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,,$$

where the limits of integration arecandr.Balancing forces as in the uniform chain produces

$$T\cos \varphi =T_{0}$$ and $$T\sin \varphi =\int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,,$$ and therefore $${\frac {dy}{dx}}=\tan \varphi ={\frac {1}{T_{0}}}\int _{\mathbf {c} }^{\mathbf {r} }w\,ds\,.$$

Differentiation then gives

$$w=T_{0}{\frac {d}{ds}}{\frac {dy}{dx}}={\frac {T_{0}{\dfrac {d^{2}y}{dx^{2}}}}{\sqrt {1+\left({\dfrac {dy}{dx}}\right)^{2}}}}\,.$$

In terms ofφand the radius of curvatureρthis becomes

$$w={\frac {T_{0}}{\rho \cos ^{2}\varphi }}\,.$$

Suspension bridge curve

Golden Gate Bridge.Mostsuspension bridgecables follow a parabolic, not a catenary curve, because the roadway is much heavier than the cable.

A similar analysis can be done to find the curve followed by the cable supporting asuspension bridgewith a horizontal roadway.If the weight of the roadway per unit length iswand the weight of the cable and the wire supporting the bridge is negligible in comparison, then the weight on the cable (see the figure inCatenary#Model of chains and arches) fromctoriswxwherexis the horizontal distance betweencandr.Proceeding as before gives the differential equation

$${\frac {dy}{dx}}=\tan \varphi ={\frac {w}{T_{0}}}x\,.$$

This is solved by simple integration to get

$$y={\frac {w}{2T_{0}}}x^{2}+\beta$$

and so the cable follows a parabola. If the weight of the cable and supporting wires is not negligible then the analysis is more complex.

Catenary of equal strength

In a catenary of equal strength, the cable is strengthened according to the magnitude of the tension at each point, so its resistance to breaking is constant along its length. Assuming that the strength of the cable is proportional to its density per unit length, the weight,w,per unit length of the chain can be written⁠T/c⁠,wherecis constant, and the analysis for nonuniform chains can be applied.

In this case the equations for tension are

$${\begin{aligned}T\cos \varphi &=T_{0}\,,\\T\sin \varphi &={\frac {1}{c}}\int T\,ds\,.\end{aligned}}$$

Combining gives

$$c\tan \varphi =\int \sec \varphi \,ds$$

and by differentiation

$$c=\rho \cos \varphi$$

whereρis the radius of curvature.

The solution to this is

$$y=c\ln \left(\sec \left({\frac {x}{c}}\right)\right)\,.$$

In this case, the curve has vertical asymptotes and this limits the span toπc.Other relations are

$$x=c\varphi \,,\quad s=\ln \left(\tan \left({\frac {\pi +2\varphi }{4}}\right)\right)\,.$$

The curve was studied 1826 byDavies Gilbertand, apparently independently, byGaspard-Gustave Coriolisin 1836.

Recently, it was shown that this type of catenary could act as a building block ofelectromagnetic metasurfaceand was known as "catenary of equal phase gradient".

Elastic catenary

In anelasticcatenary, the chain is replaced by aspringwhich can stretch in response to tension. The spring is assumed to stretch in accordance withHooke's Law.Specifically, ifpis the natural length of a section of spring, then the length of the spring with tensionTapplied has length

$$s=\left(1+{\frac {T}{E}}\right)p\,,$$

whereEis a constant equal tokp,wherekis thestiffnessof the spring.In the catenary the value ofTis variable, but ratio remains valid at a local level, so $${\frac {ds}{dp}}=1+{\frac {T}{E}}\,.$$ The curve followed by an elastic spring can now be derived following a similar method as for the inelastic spring.

The equations for tension of the spring are

$$T\cos \varphi =T_{0}\,,$$ and $$T\sin \varphi =w_{0}p\,,$$

from which

$${\frac {dy}{dx}}=\tan \varphi ={\frac {w_{0}p}{T_{0}}}\,,\quad T={\sqrt {T_{0}^{2}+w_{0}^{2}p^{2}}}\,,$$

wherepis the natural length of the segment fromctorandw₀is the weight per unit length of the spring with no tension. Write $$a={\frac {T_{0}}{w_{0}}}$$ so $${\frac {dy}{dx}}=\tan \varphi ={\frac {p}{a}}\quad {\text{and}}\quad T={\frac {T_{0}}{a}}{\sqrt {a^{2}+p^{2}}}\,.$$

Then $${\begin{aligned}{\frac {dx}{ds}}&=\cos \varphi ={\frac {T_{0}}{T}}\\[6pt]{\frac {dy}{ds}}&=\sin \varphi ={\frac {w_{0}p}{T}}\,,\end{aligned}}$$ from which $${\begin{alignedat}{3}{\frac {dx}{dp}}&={\frac {T_{0}}{T}}{\frac {ds}{dp}}&&=T_{0}\left({\frac {1}{T}}+{\frac {1}{E}}\right)&&={\frac {a}{\sqrt {a^{2}+p^{2}}}}+{\frac {T_{0}}{E}}\\[6pt]{\frac {dy}{dp}}&={\frac {w_{0}p}{T}}{\frac {ds}{dp}}&&={\frac {T_{0}p}{a}}\left({\frac {1}{T}}+{\frac {1}{E}}\right)&&={\frac {p}{\sqrt {a^{2}+p^{2}}}}+{\frac {T_{0}p}{Ea}}\,.\end{alignedat}}$$

Integrating gives the parametric equations

$${\begin{aligned}x&=a\operatorname {arsinh} \left({\frac {p}{a}}\right)+{\frac {T_{0}}{E}}p+\ Alpha \,,\\[6pt]y&={\sqrt {a^{2}+p^{2}}}+{\frac {T_{0}}{2Ea}}p^{2}+\beta \,.\end{aligned}}$$

Again, thexandy-axes can be shifted soαandβcan be taken to be 0. So

$${\begin{aligned}x&=a\operatorname {arsinh} \left({\frac {p}{a}}\right)+{\frac {T_{0}}{E}}p\,,\\[6pt]y&={\sqrt {a^{2}+p^{2}}}+{\frac {T_{0}}{2Ea}}p^{2}\end{aligned}}$$

are parametric equations for the curve. At the rigidlimitwhereEis large, the shape of the curve reduces to that of a non-elastic chain.

Other generalizations

Chain under a general force

With no assumptions being made regarding the forceGacting on the chain, the following analysis can be made.

First, letT=T(s)be the force of tension as a function ofs.The chain is flexible so it can only exert a force parallel to itself. Since tension is defined as the force that the chain exerts on itself,Tmust be parallel to the chain. In other words,

$$\mathbf {T} =T\mathbf {u} \,,$$

whereTis the magnitude ofTanduis the unit tangent vector.

Second, letG=G(s)be the external force per unit length acting on a small segment of a chain as a function ofs.The forces acting on the segment of the chain betweensands+ Δsare the force of tensionT(s+ Δs)at one end of the segment, the nearly opposite force−T(s)at the other end, and the external force acting on the segment which is approximatelyGΔs.These forces must balance so

$$\mathbf {T} (s+\Delta s)-\mathbf {T} (s)+\mathbf {G} \Delta s\approx \mathbf {0} \,.$$

Divide byΔsand take the limit asΔs→ 0to obtain

$${\frac {d\mathbf {T} }{ds}}+\mathbf {G} =\mathbf {0} \,.$$

These equations can be used as the starting point in the analysis of a flexible chain acting under any external force. In the case of the standard catenary,G= (0, −w)where the chain has weightwper unit length.

See also

• Catenary arch
• Chain fountainor self-siphoning beads
• Overhead catenary– power lines suspended over rail or tram vehicles
• Roulette (curve)– an elliptic/hyperbolic catenary
• Troposkein– the shape of a spun rope
• Weighted catenary

Bibliography

• Lockwood, E.H. (1961)."Chapter 13: The Tractrix and Catenary".A Book of Curves.Cambridge.
• Salmon, George (1879).Higher Plane Curves.Hodges, Foster and Figgis. pp.287–289.
• Routh, Edward John(1891)."Chapter X: On Strings".A Treatise on Analytical Statics.University Press.
• Maurer, Edward Rose (1914)."Art. 26 Catenary Cable".Technical Mechanics.J. Wiley & Sons.
• Lamb, Sir Horace (1897)."Art. 134 Transcendental Curves; Catenary, Tractrix".An Elementary Course of Infinitesimal Calculus.University Press.
• Todhunter, Isaac(1858)."XI Flexible Strings. Inextensible, XII Flexible Strings. Extensible".A Treatise on Analytical Statics.Macmillan.
• Whewell, William(1833)."Chapter V: The Equilibrium of a Flexible Body".Analytical Statics.J. & J.J. Deighton. p. 65.
• Weisstein, Eric W."Catenary".MathWorld.

Further reading

• Swetz, Frank (1995).Learn from the Masters.MAA. pp. 128–9.ISBN978-0-88385-703-8.
• Venturoli, Giuseppe (1822)."Chapter XXIII: On the Catenary".Elements of the Theory of Mechanics.Trans. Daniel Cresswell. J. Nicholson & Son.

External links

• O'Connor, John J.;Robertson, Edmund F.,"Catenary",MacTutor History of Mathematics Archive,University of St Andrews
• CatenaryatPlanetMath.
• Catenary curve calculator
• CatenaryatThe Geometry Center
• "Catenary" at Visual Dictionary of Special Plane Curves
• The Catenary - Chains, Arches, and Soap Films.
• Cable Sag Error Calculator– Calculates the deviation from a straight line of a catenary curve and provides derivation of the calculator and references.
• Dynamic as well as static cetenary curve equations derived– The equations governing the shape (static case) as well as dynamics (dynamic case) of a centenary is derived. Solution to the equations discussed.
• The straight line, the catenary, the brachistochrone, the circle, and FermatUnified approach to some geodesics.
• Ira Freeman "A General Form of the Suspension Bridge Catenary"Bulletin of the AMS