Cylinder

Cylinder
Cylinder
	A circular right cylinder of heighthand diameterd=2r
Type	Smooth surface; Algebraic surface
Euler char.	2
Symmetry group	O(2)×O(1)
Surface area	2πr(r + h)
Volume	πr2h

Acylinder(fromAncient Greekκύλινδρος(kúlindros)'roller, tumbler')^[1]has traditionally been athree-dimensional solid,one of the most basic ofcurvilineargeometricshapes.Inelementary geometry,it is considered aprismwith acircleas its base.

A cylinder may also be defined as aninfinitecurvilinearsurfacein various modern branches of geometry andtopology.The shift in the basic meaning—solid versus surface (as in a solidballversusspheresurface)—has created some ambiguity with terminology. The two concepts may be distinguished by referring tosolid cylindersandcylindrical surfaces.In the literature the unadorned term cylinder could refer to either of these or to an even more specialized object, theright circular cylinder.

Types[edit]

The definitions and results in this section are taken from the 1913 textPlane and Solid GeometrybyGeorge A. Wentworthand David Eugene Smith (Wentworth & Smith 1913).

Acylindrical surfaceis asurfaceconsisting of all the points on all the lines which areparallelto a given line and which pass through a fixedplane curvein a plane not parallel to the given line. Any line in this family of parallel lines is called anelementof the cylindrical surface. From akinematicspoint of view, given a plane curve, called thedirectrix,a cylindrical surface is that surface traced out by a line, called thegeneratrix,not in the plane of the directrix, moving parallel to itself and always passing through the directrix. Any particular position of the generatrix is an element of the cylindrical surface.

A right and an oblique circular cylinder

Asolidbounded by a cylindrical surface and twoparallel planesis called a (solid)cylinder.The line segments determined by an element of the cylindrical surface between the two parallel planes is called anelement of the cylinder.All the elements of a cylinder have equal lengths. The region bounded by the cylindrical surface in either of the parallel planes is called abaseof the cylinder. The two bases of a cylinder arecongruentfigures. If the elements of the cylinder are perpendicular to the planes containing the bases, the cylinder is aright cylinder,otherwise it is called anoblique cylinder.If the bases aredisks(regions whose boundary is acircle) the cylinder is called acircular cylinder.In some elementary treatments, a cylinder always means a circular cylinder.^[2]

Theheight(or altitude) of a cylinder is theperpendiculardistance between its bases.

The cylinder obtained by rotating aline segmentabout a fixed line that it is parallel to is acylinder of revolution.A cylinder of revolution is a right circular cylinder. The height of a cylinder of revolution is the length of the generating line segment. The line that the segment is revolved about is called theaxisof the cylinder and it passes through the centers of the two bases.

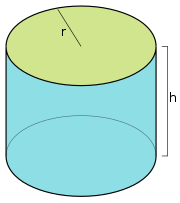
Right circular cylinders[edit]

The bare termcylinderoften refers to a solid cylinder with circular ends perpendicular to the axis, that is, a right circular cylinder, as shown in the figure. The cylindrical surface without the ends is called anopen cylinder.The formulae for thesurface areaand thevolumeof a right circular cylinder have been known from early antiquity.

A right circular cylinder can also be thought of as thesolid of revolutiongenerated by rotating a rectangle about one of its sides. These cylinders are used in an integration technique (the "disk method" ) for obtaining volumes of solids of revolution.^[3]

A tall and thinneedle cylinderhas a height much greater than its diameter, whereas a short and widedisk cylinderhas a diameter much greater than its height.

Properties[edit]

Cylindric sections[edit]

A cylindric section is the intersection of a cylinder's surface with aplane.They are, in general, curves and are special types ofplane sections.The cylindric section by a plane that contains two elements of a cylinder is aparallelogram.^[4]Such a cylindric section of a right cylinder is arectangle.^[4]

A cylindric section in which the intersecting plane intersects and is perpendicular to all the elements of the cylinder is called aright section.^[5]If a right section of a cylinder is a circle then the cylinder is a circular cylinder. In more generality, if a right section of a cylinder is aconic section(parabola, ellipse, hyperbola) then the solid cylinder is said to be parabolic, elliptic and hyperbolic, respectively.

For a right circular cylinder, there are several ways in which planes can meet a cylinder. First, planes that intersect a base in at most one point. A plane is tangent to the cylinder if it meets the cylinder in a single element. The right sections are circles and all other planes intersect the cylindrical surface in anellipse.^[6]If a plane intersects a base of the cylinder in exactly two points then the line segment joining these points is part of the cylindric section. If such a plane contains two elements, it has a rectangle as a cylindric section, otherwise the sides of the cylindric section are portions of an ellipse. Finally, if a plane contains more than two points of a base, it contains the entire base and the cylindric section is a circle.

In the case of a right circular cylinder with a cylindric section that is an ellipse, theeccentricity $e$ of the cylindric section andsemi-major axis $a$ of the cylindric section depend on the radius of the cylinder $r$ and the angle $α$ between the secant plane and cylinder axis, in the following way: ${\begin{aligned}e&=\cos \ Alpha,\\[1ex]a&={\frac {r}{\sin \ Alpha }}.\end{aligned}}$

Volume[edit]

If the base of a circular cylinder has aradius $r$ and the cylinder has height $h$ ,then itsvolumeis given by $V=\pi r^{2}h$

This formula holds whether or not the cylinder is a right cylinder.^[7]

This formula may be established by usingCavalieri's principle.

In more generality, by the same principle, the volume of any cylinder is the product of the area of a base and the height. For example, an elliptic cylinder with a base havingsemi-major axis $a$ ,semi-minor axis $b$ and height $h$ has a volume $V = Ah$ ,where $A$ is the area of the base ellipse (= $π ab$ ). This result for right elliptic cylinders can also be obtained by integration, where the axis of the cylinder is taken as the positive $x$ -axis and $A (x) = A$ the area of each elliptic cross-section, thus: $V=\int _{0}^{h}A(x)dx=\int _{0}^{h}\pi abdx=\pi ab\int _{0}^{h}dx=\pi abh.$

Usingcylindrical coordinates,the volume of a right circular cylinder can be calculated by integration ${\begin{aligned}V&=\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz\\[5mu]&=\pi \,r^{2}\,h.\end{aligned}}$

Surface area[edit]

Having radius $r$ and altitude (height) $h$ ,thesurface areaof a right circular cylinder, oriented so that its axis is vertical, consists of three parts:

the area of the top base: $π r 2$
the area of the bottom base: $π r 2$
the area of the side: $2π rh$

The area of the top and bottom bases is the same, and is called thebase area, $B$ .The area of the side is known as thelateral area, $L$ .

Anopen cylinderdoes not include either top or bottom elements, and therefore has surface area (lateral area) $L=2\pi rh$

The surface area of the solid right circular cylinder is made up the sum of all three components: top, bottom and side. Its surface area is therefore $A=L+2B=2\pi rh+2\pi r^{2}=2\pi r(h+r)=\pi d(r+h)$ where $d = 2 r$ is thediameterof the circular top or bottom.

For a given volume, the right circular cylinder with the smallest surface area has $h = 2 r$ .Equivalently, for a given surface area, the right circular cylinder with the largest volume has $h = 2 r$ ,that is, the cylinder fits snugly in a cube of side length = altitude ( = diameter of base circle).^[8]

The lateral area, $L$ ,of a circular cylinder, which need not be a right cylinder, is more generally given by $L=e\times p,$ where $e$ is the length of an element and $p$ is the perimeter of a right section of the cylinder.^[9]This produces the previous formula for lateral area when the cylinder is a right circular cylinder.

Right circular hollow cylinder (cylindrical shell)[edit]

Aright circular hollow cylinder(orcylindrical shell) is a three-dimensional region bounded by two right circular cylinders having the same axis and two parallelannularbases perpendicular to the cylinders' common axis, as in the diagram.

Let the height be $h$ ,internal radius $r$ ,and external radius $R$ .The volume is given by $V=\pi \left(R^{2}-r^{2}\right)h=2\pi \left({\frac {R+r}{2}}\right)h(R-r).$ Thus, the volume of a cylindrical shell equals2 $π$ × average radius × altitude × thickness.^[10]

The surface area, including the top and bottom, is given by $A=2\pi \left(R+r\right)h+2\pi \left(R^{2}-r^{2}\right).$ Cylindrical shells are used in a common integration technique for finding volumes of solids of revolution.^[11]

On the Sphere and Cylinder[edit]

In the treatise by this name, writtenc. 225 BCE,Archimedesobtained the result of which he was most proud, namely obtaining the formulas for the volume and surface area of asphereby exploiting the relationship between a sphere and itscircumscribed right circular cylinderof the same height anddiameter.The sphere has a volumetwo-thirdsthat of the circumscribed cylinder and a surface areatwo-thirdsthat of the cylinder (including the bases). Since the values for the cylinder were already known, he obtained, for the first time, the corresponding values for the sphere. The volume of a sphere of radius $r$ is $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠4/3⁠πr3=⁠2/3⁠(2πr3)$ .The surface area of this sphere is $4 π r 2 = ⁠ 2 / 3 ⁠ (6 π r 2)$ .A sculpted sphere and cylinder were placed on the tomb of Archimedes at his request.

Cylindrical surfaces[edit]

In some areas of geometry and topology the termcylinderrefers to what has been called acylindrical surface.A cylinder is defined as a surface consisting of all the points on all the lines which are parallel to a given line and which pass through a fixed plane curve in a plane not parallel to the given line.^[12]Such cylinders have, at times, been referred to asgeneralized cylinders.Through each point of a generalized cylinder there passes a unique line that is contained in the cylinder.^[13]Thus, this definition may be rephrased to say that a cylinder is anyruled surfacespanned by a one-parameter family of parallel lines.

A cylinder having a right section that is anellipse,parabola,orhyperbolais called anelliptic cylinder,parabolic cylinderandhyperbolic cylinder,respectively. These are degeneratequadric surfaces.^[14]

When the principal axes of a quadric are aligned with the reference frame (always possible for a quadric), a general equation of the quadric in three dimensions is given by $f(x,y,z)=Ax^{2}+By^{2}+Cz^{2}+Dx+Ey+Gz+H=0,$ with the coefficients beingreal numbersand not all of $A$ , $B$ and $C$ being 0. If at least one variable does not appear in the equation, then the quadric is degenerate. If one variable is missing, we may assume by an appropriaterotation of axesthat the variable $z$ does not appear and the general equation of this type of degenerate quadric can be written as^[15] $A\left(x+{\frac {D}{2A}}\right)^{2}+B\left(y+{\frac {E}{2B}}\right)^{2}=\rho,$ where $\rho =-H+{\frac {D^{2}}{4A}}+{\frac {E^{2}}{4B}}.$

Elliptic cylinder[edit]

If $AB > 0$ this is the equation of anelliptic cylinder.^[15]Further simplification can be obtained bytranslation of axesand scalar multiplication. If $\rho$ has the same sign as the coefficients $A$ and $B$ ,then the equation of an elliptic cylinder may be rewritten inCartesian coordinatesas: $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.$ This equation of an elliptic cylinder is a generalization of the equation of the ordinary,circular cylinder( $a = b$ ). Elliptic cylinders are also known ascylindroids,but that name is ambiguous, as it can also refer to thePlücker conoid.

If $\rho$ has a different sign than the coefficients, we obtain theimaginary elliptic cylinders: $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1,$ which have no real points on them. ( $\rho =0$ gives a single real point.)

Hyperbolic cylinder[edit]

If $A$ and $B$ have different signs and $\rho \neq 0$ ,we obtain thehyperbolic cylinders,whose equations may be rewritten as: $\left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1.$

Parabolic cylinder[edit]

Finally, if $AB = 0$ assume,without loss of generality,that $B = 0$ and $A = 1$ to obtain theparabolic cylinderswith equations that can be written as:^[16] $x^{2}+2ay=0.$

Projective geometry[edit]

Inprojective geometry,a cylinder is simply aconewhoseapex(vertex) lies on theplane at infinity.If the cone is a quadratic cone, the plane at infinity (which passes through the vertex) can intersect the cone at two real lines, a single real line (actually a coincident pair of lines), or only at the vertex. These cases give rise to the hyperbolic, parabolic or elliptic cylinders respectively.^[17]

This concept is useful when consideringdegenerate conics,which may include the cylindrical conics.

Prisms[edit]

Tycho Brahe Planetariumbuilding, Copenhagen, is an example of a truncated cylinder

Asolid circular cylindercan be seen as the limiting case of a $n$ -gonalprism where $n$ approachesinfinity.The connection is very strong and many older texts treatprismsand cylinders simultaneously. Formulas for surface area and volume are derived from the corresponding formulas for prisms by using inscribed and circumscribed prisms and then letting the number of sides of the prism increase without bound.^[18]One reason for the early emphasis (and sometimes exclusive treatment) on circular cylinders is that a circular base is the only type of geometric figure for which this technique works with the use of only elementary considerations (no appeal to calculus or more advanced mathematics). Terminology about prisms and cylinders is identical. Thus, for example, since atruncated prismis a prism whose bases do not lie in parallel planes, a solid cylinder whose bases do not lie in parallel planes would be called atruncated cylinder.

From a polyhedral viewpoint, a cylinder can also be seen as adualof abiconeas an infinite-sidedbipyramid.

Family ofuniformn-gonalprisms v t e
Prism name	Digonal prism	(Trigonal) Triangular prism	(Tetragonal) Square prism	Pentagonal prism	Hexagonal prism	Heptagonal prism	Octagonal prism	Enneagonal prism	Decagonal prism	Hendecagonal prism	Dodecagonal prism	...	Apeirogonal prism
Polyhedron image												...
Spherical tiling image												Plane tiling image
Vertex config.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
Coxeter diagram												...

Notes[edit]

^κύλινδρος Archived2013-07-30 at theWayback Machine,Henry George Liddell, Robert Scott,A Greek-English Lexicon,on Perseus
^Jacobs, Harold R. (1974),Geometry,W. H. Freeman and Co., p. 607,ISBN 0-7167-0456-0
^Swokowski 1983,p. 283.
^^a ^bWentworth & Smith 1913,p. 354.
^Wentworth & Smith 1913,p. 357.
^"Cylindric section",MathWorld
^Wentworth & Smith 1913,p. 359.
^Lax, Peter D.;Terrell, Maria Shea (2013),Calculus With Applications,Springer, p. 178,ISBN 9781461479468.
^Wentworth & Smith 1913,p. 358.
^Swokowski 1983,p. 292.
^Swokowski 1983,p. 291.
^Albert 2016,p. 43.
^Albert 2016,p. 49.
^Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1999),Geometry,Cambridge University Press, p. 34,ISBN 978-0-521-59787-6
^^a ^bAlbert 2016,p. 74.
^Albert 2016,p. 75.
^Pedoe, Dan (1988) [1970],Geometry a Comprehensive Course,Dover, p. 398,ISBN 0-486-65812-0
^Slaught, H.E.;Lennes, N.J. (1919),Solid Geometry with Problems and Applications(PDF)(Rev. ed.), Allyn and Bacon, pp. 79–81

References[edit]

Albert, Abraham Adrian (2016) [1949],Solid Analytic Geometry,Dover,ISBN 978-0-486-81026-3
Swokowski, Earl W. (1983),Calculus with Analytic Geometry(Alternate ed.), Prindle, Weber & Schmidt,ISBN 0-87150-341-7
Wentworth, George; Smith, David Eugene (1913),Plane and Solid Geometry,Ginn and Co.

External links[edit]

[1] κύλινδρος Archived2013-07-30 at theWayback Machine,Henry George Liddell, Robert Scott,A Greek-English Lexicon,on Perseus

[2] Jacobs, Harold R. (1974),Geometry,W. H. Freeman and Co., p. 607,ISBN 0-7167-0456-0

[FOOTNOTESwokowski1983283-3] Swokowski 1983,p. 283.

[FOOTNOTEWentworthSmith1913354-4] Wentworth & Smith 1913,p. 354.

[FOOTNOTEWentworthSmith1913357-5] Wentworth & Smith 1913,p. 357.

[6] "Cylindric section",MathWorld

[FOOTNOTEWentworthSmith1913359-7] Wentworth & Smith 1913,p. 359.

[8] Lax, Peter D.;Terrell, Maria Shea (2013),Calculus With Applications,Springer, p. 178,ISBN 9781461479468.

[FOOTNOTEWentworthSmith1913358-9] Wentworth & Smith 1913,p. 358.

[FOOTNOTESwokowski1983292-10] Swokowski 1983,p. 292.

[FOOTNOTESwokowski1983291-11] Swokowski 1983,p. 291.

[FOOTNOTEAlbert201643-12] Albert 2016,p. 43.

[FOOTNOTEAlbert201649-13] Albert 2016,p. 49.

[14] Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1999),Geometry,Cambridge University Press, p. 34,ISBN 978-0-521-59787-6

[FOOTNOTEAlbert201674-15] Albert 2016,p. 74.

[FOOTNOTEAlbert201675-16] Albert 2016,p. 75.

[17] Pedoe, Dan (1988) [1970],Geometry a Comprehensive Course,Dover, p. 398,ISBN 0-486-65812-0

[18] Slaught, H.E.;Lennes, N.J. (1919),Solid Geometry with Problems and Applications(PDF)(Rev. ed.), Allyn and Bacon, pp. 79–81

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]