Derangement

For the psychological condition, seepsychosis.

Number of possible permutations and derangements ofnelements.n!(nfactorial) is the number ofn-permutations;!n(nsubfactorial) is the number of derangements –n-permutations where all of thenelements change their initial places.

Table of values
$n$	Permutations,$n!$	Derangements,${\displaystyle!n}$	${\frac {!n}{n!}}$
0	1=1×100	1=1×100	= 1
1	1=1×100	0	= 0
2	2=2×100	1=1×100	= 0.5
3	6=6×100	2=2×100	≈0.33333 33333
4	24=2.4×101	9=9×100	= 0.375
5	120=1.20×102	44=4.4×101	≈0.36666 66667
6	720=7.20×102	265=2.65×102	≈0.36805 55556
7	5,040=5.04×103	1,854≈1.85×103	≈0.36785,71429
8	40,320≈4.03×104	14,833≈1.48×104	≈0.36788 19444
9	362,880≈3.63×105	133,496≈1.33×105	≈0.36787 91887
10	3,628,800≈3.63×106	1,334,961≈1.33×106	≈0.36787 94643
11	39,916,800≈3.99×107	14,684,570≈1.47×107	≈0.36787 94392
12	479,001,600≈4.79×108	176,214,841≈1.76×108	≈0.36787 94413
13	6,227,020,800≈6.23×109	2,290,792,932≈2.29×109	≈0.36787 94412
14	87,178,291,200≈8.72×1010	32,071,101,049≈3.21×1010	≈0.36787 94412
15	1,307,674,368,000≈1.31×1012	481,066,515,734≈4.81×1011	≈0.36787 94412
16	20,922,789,888,000≈2.09×1013	7,697,064,251,745≈7.70×1012	≈0.36787 94412
17	355,687,428,096,000≈3.56×1014	130,850,092,279,664≈1.31×1014	≈0.36787 94412
18	6,402,373,705,728,000≈6.40×1015	2,355,301,661,033,953≈2.36×1015	≈0.36787 94412
19	121,645,100,408,832,000≈1.22×1017	44,750,731,559,645,106≈4.48×1016	≈0.36787 94412
20	2,432,902,008,176,640,000≈2.43×1018	895,014,631,192,902,121≈8.95×1017	≈0.36787 94412
21	51,090,942,171,709,440,000≈5.11×1019	18,795,307,255,050,944,540≈1.88×1019	≈0.36787 94412
22	1,124,000,727,777,607,680,000≈1.12×1021	413,496,759,611,120,779,881≈4.13×1020	≈0.36787 94412
23	25,852,016,738,884,976,640,000≈2.59×1022	9,510,425,471,055,777,937,262≈9.51×1021	≈0.36787 94412
24	620,448,401,733,239,439,360,000≈6.20×1023	228,250,211,305,338,670,494,289≈2.28×1023	≈0.36787 94412
25	15,511,210,043,330,985,984,000,000≈1.55×1025	5,706,255,282,633,466,762,357,224≈5.71×1024	≈0.36787 94412
26	403,291,461,126,605,635,584,000,000≈4.03×1026	148,362,637,348,470,135,821,287,825≈1.48×1026	≈0.36787 94412
27	10,888,869,450,418,352,160,768,000,000≈1.09×1028	4,005,791,208,408,693,667,174,771,274≈4.01×1027	≈0.36787 94412
28	304,888,344,611,713,860,501,504,000,000≈3.05×1029	112,162,153,835,443,422,680,893,595,673≈1.12×1029	≈0.36787 94412
29	8,841,761,993,739,701,954,543,616,000,000≈8.84×1030	3,252,702,461,227,859,257,745,914,274,516≈3.25×1030	≈0.36787 94412
30	265,252,859,812,191,058,636,308,480,000,000≈2.65×1032	97,581,073,836,835,777,732,377,428,235,481≈9.76×1031	≈0.36787 94412

Incombinatorialmathematics,aderangementis apermutationof the elements of asetin which no element appears in its original position. In other words, a derangement is a permutation that has nofixed points.

The number of derangements of a set of sizenis known as thesubfactorialofnor then-thderangement numberorn-thde Montmort number(afterPierre Remond de Montmort). Notations for subfactorials in common use include!n,D_n,d_n,orn¡.

Forn> 0, the subfactorial!nequals the nearest integer ton!/e,wheren!denotes thefactorialofnandeisEuler's number.

The problem of counting derangements was first considered byPierre Raymond de Montmortin hisEssay d'analyse sur les jeux de hazard.in 1708; he solved it in 1713, as didNicholas Bernoulliat about the same time.

Example

The 9 derangements (from 24 permutations) are highlighted.

Suppose that a professor gave a test to 4 students – A, B, C, and D – and wants to let them grade each other's tests. Of course, no student should grade their own test. How many ways could the professor hand the tests back to the students for grading, such that no student received their own test back? Out of24 possible permutations(4!) for handing back the tests,

ABCD,	ABDC,	ACBD,	ACDB,	ADBC,	ADCB,
BACD,	BADC,	BCAD,	BCDA,	BDAC,	BDCA,
CABD,	CADB,	CBAD,	CBDA,	CDAB,	CDBA,
DABC,	DACB,	DBAC,	DBCA,	DCAB,	DCBA.

there are only 9 derangements (shown in blue italics above). In every other permutation of this 4-member set, at least one student gets their own test back (shown in bold red).

Another version of the problem arises when we ask for the number of waysnletters, each addressed to a different person, can be placed innpre-addressed envelopes so that no letter appears in the correctly addressed envelope.

Counting derangements

Counting derangements of a set amounts to thehat-check problem,in which one considers the number of ways in whichnhats (call themh₁throughh_n) can be returned tonpeople (P₁throughP_n) such that no hat makes it back to its owner.

Each person may receive any of then− 1 hats that is not their own. Call the hat which the personP₁receivesh_iand considerh_i's owner:P_ireceives eitherP₁'s hat,h₁,or some other. Accordingly, the problem splits into two possible cases:

1. P_ireceives a hat other thanh₁.This case is equivalent to solving the problem withn− 1 people andn− 1 hats because for each of then− 1 people besidesP₁there is exactly one hat from among the remainingn− 1 hats that they may not receive (for anyP_jbesidesP_i,the unreceivable hat ish_j,while forP_iit ish₁). Another way to see this is to renameh₁toh_i,where the derangement is more explicit: for anyjfrom 2 ton,P_jcannot receiveh_j.
2. P_ireceivesh₁.In this case the problem reduces ton− 2 people andn− 2 hats, becauseP₁receivedh_i's hat andP_ireceivedh₁'s hat, effectively putting both out of further consideration.

For each of then− 1 hats thatP₁may receive, the number of ways thatP₂,...,P_nmay all receive hats is the sum of the counts for the two cases.

This gives us the solution to the hat-check problem: stated algebraically, the number!nof derangements of ann-element set is

${\displaystyle!n=(n-1)\cdot ({!(n-1)}+{!(n-2)})}$for$n\geq 2$,

where${\displaystyle!0=1}$and${\displaystyle!1=0}$.

The number of derangements of small lengths is given in the table below.

The number of derangements of ann-element set (sequenceA000166in theOEIS) for smalln

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13
!n	1	0	1	2	9	44	265	1,854	14,833	133,496	1,334,961	14,684,570	176,214,841	2,290,792,932

There are various other expressions for!n,equivalent to the formula given above. These include

${\displaystyle!n=n!\sum _{i=0}^{n}{\frac {(-1)^{i}}{i!}}}$for$n\geq 0$

and

${\displaystyle!n=\left[{\frac {n!}{e}}\right]=\left\lfloor {\frac {n!}{e}}+{\frac {1}{2}}\right\rfloor }$for$n\geq 1,$

where$\left[x\right]$is thenearest integer functionand$\left\lfloor x\right\rfloor$is thefloor function.

Other related formulas include $${\displaystyle!n=\left\lfloor {\frac {n!+1}{e}}\right\rfloor,\quad \ n\geq 1,}$$ $${\displaystyle!n=\left\lfloor \left(e+e^{-1}\right)n!\right\rfloor -\lfloor en!\rfloor,\quad n\geq 2,}$$ and $${\displaystyle!n=n!-\sum _{i=1}^{n}{n \choose i}\cdot {!(n-i)},\quad \ n\geq 1.}$$

The following recurrence also holds: $${\displaystyle!n={\begin{cases}1&{\text{if }}n=0,\\n\cdot \left(!(n-1)\right)+(-1)^{n}&{\text{if }}n>0.\end{cases}}}$$

Derivation by inclusion–exclusion principle

One may derive a non-recursive formula for the number of derangements of ann-set, as well. For$1\leq k\leq n$we define$S_{k}$to be the set of permutations ofnobjects that fix the$k$-th object. Any intersection of a collection ofiof these sets fixes a particular set ofiobjects and therefore contains$(n-i)!$permutations. There are${\textstyle {n \choose i}}$such collections, so theinclusion–exclusion principleyields $${\begin{aligned}|S_{1}\cup \dotsm \cup S_{n}|&=\sum _{i}\left|S_{i}\right|-\sum _{i<j}\left|S_{i}\cap S_{j}\right|+\sum _{i<j<k}\left|S_{i}\cap S_{j}\cap S_{k}\right|+\cdots +(-1)^{n+1}\left|S_{1}\cap \dotsm \cap S_{n}\right|\\&={n \choose 1}(n-1)!-{n \choose 2}(n-2)!+{n \choose 3}(n-3)!-\cdots +(-1)^{n+1}{n \choose n}0!\\&=\sum _{i=1}^{n}(-1)^{i+1}{n \choose i}(n-i)!\\&=n!\ \sum _{i=1}^{n}{(-1)^{i+1} \over i!},\end{aligned}}$$ and since a derangement is a permutation that leaves none of thenobjects fixed, this implies $${\displaystyle!n=n!-\left|S_{1}\cup \dotsm \cup S_{n}\right|=n!\sum _{i=0}^{n}{\frac {(-1)^{i}}{i!}}.}$$

On the other hand,$n!=\sum _{i=0}^{n}{\binom {n}{i}}!i$since we can choose n - i elements to be in their own place and derange the other i elements in just!i ways, by definition.

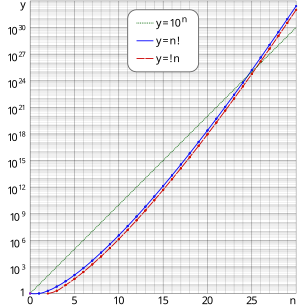
Growth of number of derangements asnapproaches ∞

From $${\displaystyle!n=n!\sum _{i=0}^{n}{\frac {(-1)^{i}}{i!}}}$$ and $$e^{x}=\sum _{i=0}^{\infty }{x^{i} \over i!}$$ by substituting$\textstyle x=-1$one immediately obtains that $$\lim _{n\to \infty }{!n \over n!}=\lim _{n\to \infty }\sum _{i=0}^{n}{\frac {(-1)^{i}}{i!}}=e^{-1}\approx 0.367879\ldots.$$ This is the limit of theprobabilitythat a randomly selected permutation of a large number of objects is a derangement. The probability converges to this limit extremely quickly asnincreases, which is why!nis the nearest integer ton!/e.The abovesemi-loggraph shows that the derangement graph lags the permutation graph by an almost constant value.

More information about this calculation and the above limit may be found in the article on the statistics of random permutations.

Asymptotic expansion in terms of Bell numbers

An asymptotic expansion for the number ofderangementsin terms ofBell numbersis as follows: $${\displaystyle!n={\frac {n!}{e}}+\sum _{k=1}^{m}\left(-1\right)^{n+k-1}{\frac {B_{k}}{n^{k}}}+O\left({\frac {1}{n^{m+1}}}\right),}$$ where$m$is any fixed positive integer, and$B_{k}$denotes the$k$-thBell number.Moreover, the constant implied by thebig O-term does not exceed$B_{m+1}$.

Generalizations

Theproblème des rencontresasks how many permutations of a size-nset have exactlykfixed points.

Derangements are an example of the wider field of constrained permutations. For example, theménage problemasks ifnopposite-sex couples are seated man-woman-man-woman-... around a table, how many ways can they be seated so that nobody is seated next to his or her partner?

More formally, given setsAandS,and some setsUandVofsurjectionsA→S,we often wish to know the number of pairs of functions (f,g) such thatfis inUandgis inV,and for allainA,f(a) ≠g(a); in other words, where for eachfandg,there exists a derangement φ ofSsuch thatf(a) = φ(g(a)).

Another generalization is the following problem:

How many anagrams with no fixed letters of a given word are there?

For instance, for a word made of only two different letters, saynletters A andmletters B, the answer is, of course, 1 or 0 according to whethern=mor not, for the only way to form an anagram without fixed letters is to exchange all theAwithB,which is possible if and only ifn=m.In the general case, for a word withn₁lettersX₁,n₂lettersX₂,...,n_rlettersX_r,it turns out (after a proper use of theinclusion-exclusionformula) that the answer has the form $$\int _{0}^{\infty }P_{n_{1}}(x)P_{n_{2}}(x)\cdots P_{n_{r}}(x)e^{-x}\,dx,$$ for a certain sequence of polynomialsP_n,whereP_nhas degreen.But the above answer for the caser= 2 gives an orthogonality relation, whence theP_n's are theLaguerre polynomials(up toa sign that is easily decided).

$\int _{0}^{\infty }(t-1)^{z}e^{-t}dt$in the complex plane

In particular, for the classical derangements, one has that $${\displaystyle!n={\frac {\Gamma (n+1,-1)}{e}}=\int _{0}^{\infty }(x-1)^{n}e^{-x}dx}$$ where$\Gamma (s,x)$is theupper incomplete gamma function.

Computational complexity

It isNP-completeto determine whether a givenpermutation group(described by a given set of permutations that generate it) contains any derangements.

External links

• Baez, John(2003)."Let's get deranged!"(PDF).
• Bogart, Kenneth P.; Doyle, Peter G. (1985)."Non-sexist solution of the ménage problem".
• Weisstein, Eric W."Derangement".MathWorld–A Wolfram Web Resource.