Unit vector

Not to be confused withVector of ones.

Inmathematics,aunit vectorin anormed vector spaceis avector(often aspatial vector) oflength1. A unit vector is often denoted by a lowercase letter with acircumflex,or "hat", as in${\hat {\mathbf {v} }}$(pronounced "v-hat" ).

The termdirection vector,commonly denoted asd,is used to describe a unit vector being used to representspatial directionandrelative direction.2D spatial directions are numerically equivalent to points on theunit circle and spatial directions in 3D are equivalent to a point on theunit sphere.

Examples of two 2D direction vectors

Examples of two 3D direction vectors

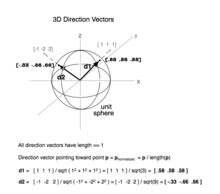
Thenormalized vector ûof a non-zero vectoruis the unit vector in the direction ofu,i.e.,

$\mathbf {\hat {u}} ={\frac {\mathbf {u} }{\|\mathbf {u} \|}}$

where ‖u‖ is thenorm(or length) ofu.The termnormalized vectoris sometimes used as a synonym forunit vector.

Unit vectors are often chosen to form thebasisof a vector space, and every vector in the space may be written as alinear combinationform of unit vectors.

Orthogonal coordinates

Cartesian coordinates

Main article:Standard basis

Unit vectors may be used to represent the axes of aCartesian coordinate system.For instance, the standard unit vectors in the direction of thex,y,andzaxes of a three dimensional Cartesian coordinate system are

$\mathbf {\hat {x}} ={\begin{bmatrix}1\\0\\0\end{bmatrix}},\,\,\mathbf {\hat {y}} ={\begin{bmatrix}0\\1\\0\end{bmatrix}},\,\,\mathbf {\hat {z}} ={\begin{bmatrix}0\\0\\1\end{bmatrix}}$

They form a set of mutuallyorthogonalunit vectors, typically referred to as astandard basisinlinear algebra.

They are often denoted using common vector notation (e.g.,xor${\vec {x}}$) rather than standard unit vector notation (e.g.,x̂). In most contexts it can be assumed thatx,y,andz,(or${\vec {x}},$${\vec {y}},$and${\vec {z}}$) are versors of a 3-D Cartesian coordinate system. The notations (î,ĵ,k̂), (x̂₁,x̂₂,x̂₃), (ê_x,ê_y,ê_z), or (ê₁,ê₂,ê₃), with or withouthat,are also used,particularly in contexts wherei,j,kmight lead to confusion with another quantity (for instance withindexsymbols such asi,j,k,which are used to identify an element of a set or array or sequence of variables).

When a unit vector in space is expressed inCartesian notationas a linear combination ofx,y,z,its three scalar components can be referred to asdirection cosines.The value of each component is equal to the cosine of the angle formed by the unit vector with the respective basis vector. This is one of the methods used to describe theorientation(angular position) of a straight line, segment of straight line, oriented axis, or segment of oriented axis (vector).

Cylindrical coordinates

See also:Jacobian matrix

The threeorthogonalunit vectors appropriate to cylindrical symmetry are:

• ${\boldsymbol {\hat {\rho }}}$(also designated$\mathbf {\hat {e}}$or${\boldsymbol {\hat {s}}}$), representing the direction along which the distance of the point from the axis of symmetry is measured;
• ${\boldsymbol {\hat {\varphi }}}$,representing the direction of the motion that would be observed if the point were rotating counterclockwise about thesymmetry axis;
• $\mathbf {\hat {z}}$,representing the direction of the symmetry axis;

They are related to the Cartesian basis${\hat {x}}$,${\hat {y}}$,${\hat {z}}$by:

${\boldsymbol {\hat {\rho }}}=\cos(\varphi )\mathbf {\hat {x}} +\sin(\varphi )\mathbf {\hat {y}}$

${\boldsymbol {\hat {\varphi }}}=-\sin(\varphi )\mathbf {\hat {x}} +\cos(\varphi )\mathbf {\hat {y}}$

$\mathbf {\hat {z}} =\mathbf {\hat {z}}.$

The vectors${\boldsymbol {\hat {\rho }}}$and${\boldsymbol {\hat {\varphi }}}$are functions of$\varphi,$and arenotconstant in direction. When differentiating or integrating in cylindrical coordinates, these unit vectors themselves must also be operated on. The derivatives with respect to$\varphi$are:

${\frac {\partial {\boldsymbol {\hat {\rho }}}}{\partial \varphi }}=-\sin \varphi \mathbf {\hat {x}} +\cos \varphi \mathbf {\hat {y}} ={\boldsymbol {\hat {\varphi }}}$

${\frac {\partial {\boldsymbol {\hat {\varphi }}}}{\partial \varphi }}=-\cos \varphi \mathbf {\hat {x}} -\sin \varphi \mathbf {\hat {y}} =-{\boldsymbol {\hat {\rho }}}$

${\frac {\partial \mathbf {\hat {z}} }{\partial \varphi }}=\mathbf {0}.$

Spherical coordinates

The unit vectors appropriate to spherical symmetry are:$\mathbf {\hat {r}}$,the direction in which the radial distance from the origin increases;${\boldsymbol {\hat {\varphi }}}$,the direction in which the angle in thex-yplane counterclockwise from the positivex-axis is increasing; and${\boldsymbol {\hat {\theta }}}$,the direction in which the angle from the positivezaxis is increasing. To minimize redundancy of representations, the polar angle$\theta$is usually taken to lie between zero and 180 degrees. It is especially important to note the context of any ordered triplet written inspherical coordinates,as the roles of${\boldsymbol {\hat {\varphi }}}$and${\boldsymbol {\hat {\theta }}}$are often reversed. Here, the American "physics" conventionis used. This leaves theazimuthal angle$\varphi$defined the same as in cylindrical coordinates. TheCartesianrelations are:

$\mathbf {\hat {r}} =\sin \theta \cos \varphi \mathbf {\hat {x}} +\sin \theta \sin \varphi \mathbf {\hat {y}} +\cos \theta \mathbf {\hat {z}}$

${\boldsymbol {\hat {\theta }}}=\cos \theta \cos \varphi \mathbf {\hat {x}} +\cos \theta \sin \varphi \mathbf {\hat {y}} -\sin \theta \mathbf {\hat {z}}$

${\boldsymbol {\hat {\varphi }}}=-\sin \varphi \mathbf {\hat {x}} +\cos \varphi \mathbf {\hat {y}}$

The spherical unit vectors depend on both$\varphi$and$\theta$,and hence there are 5 possible non-zero derivatives. For a more complete description, seeJacobian matrix and determinant.The non-zero derivatives are:

${\frac {\partial \mathbf {\hat {r}} }{\partial \varphi }}=-\sin \theta \sin \varphi \mathbf {\hat {x}} +\sin \theta \cos \varphi \mathbf {\hat {y}} =\sin \theta {\boldsymbol {\hat {\varphi }}}$

${\frac {\partial \mathbf {\hat {r}} }{\partial \theta }}=\cos \theta \cos \varphi \mathbf {\hat {x}} +\cos \theta \sin \varphi \mathbf {\hat {y}} -\sin \theta \mathbf {\hat {z}} ={\boldsymbol {\hat {\theta }}}$

${\frac {\partial {\boldsymbol {\hat {\theta }}}}{\partial \varphi }}=-\cos \theta \sin \varphi \mathbf {\hat {x}} +\cos \theta \cos \varphi \mathbf {\hat {y}} =\cos \theta {\boldsymbol {\hat {\varphi }}}$

${\frac {\partial {\boldsymbol {\hat {\theta }}}}{\partial \theta }}=-\sin \theta \cos \varphi \mathbf {\hat {x}} -\sin \theta \sin \varphi \mathbf {\hat {y}} -\cos \theta \mathbf {\hat {z}} =-\mathbf {\hat {r}}$

${\frac {\partial {\boldsymbol {\hat {\varphi }}}}{\partial \varphi }}=-\cos \varphi \mathbf {\hat {x}} -\sin \varphi \mathbf {\hat {y}} =-\sin \theta \mathbf {\hat {r}} -\cos \theta {\boldsymbol {\hat {\theta }}}$

General unit vectors

Main article:Orthogonal coordinates

Common themes of unit vectors occur throughoutphysicsandgeometry:

Unit vector	Nomenclature	Diagram
Tangent vector to a curve/flux line	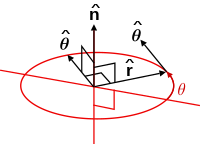$\mathbf {\hat {t}}$	A normal vector$\mathbf {\hat {n}}$to the plane containing and defined by the radial position vector$r\mathbf {\hat {r}}$and angular tangential direction of rotation$\theta {\boldsymbol {\hat {\theta }}}$is necessary so that the vector equations of angular motion hold.
Normal to a surface tangent plane/plane containing radial position component and angular tangential component	$\mathbf {\hat {n}}$ In terms ofpolar coordinates; $\mathbf {\hat {n}} =\mathbf {\hat {r}} \times {\boldsymbol {\hat {\theta }}}$
Binormal vector to tangent and normal	$\mathbf {\hat {b}} =\mathbf {\hat {t}} \times \mathbf {\hat {n}}$
Parallel to some axis/line	$\mathbf {\hat {e}} _{\parallel }$	One unit vector$\mathbf {\hat {e}} _{\parallel }$aligned parallel to a principal direction (red line), and a perpendicular unit vector$\mathbf {\hat {e}} _{\bot }$is in any radial direction relative to the principal line.
Perpendicular to some axis/line in some radial direction	$\mathbf {\hat {e}} _{\bot }$
Possible angular deviation relative to some axis/line	$\mathbf {\hat {e}} _{\angle }$	Unit vector at acute deviation angleφ(including 0 orπ/2 rad) relative to a principal direction.

Curvilinear coordinates

In general, a coordinate system may be uniquely specified using a number oflinearly independentunit vectors$\mathbf {\hat {e}} _{n}$(the actual number being equal to the degrees of freedom of the space). For ordinary 3-space, these vectors may be denoted$\mathbf {\hat {e}} _{1},\mathbf {\hat {e}} _{2},\mathbf {\hat {e}} _{3}$.It is nearly always convenient to define the system to be orthonormal andright-handed:

$\mathbf {\hat {e}} _{i}\cdot \mathbf {\hat {e}} _{j}=\delta _{ij}$

$\mathbf {\hat {e}} _{i}\cdot (\mathbf {\hat {e}} _{j}\times \mathbf {\hat {e}} _{k})=\varepsilon _{ijk}$

where$\delta _{ij}$is theKronecker delta(which is 1 fori=j,and 0 otherwise) and$\varepsilon _{ijk}$is theLevi-Civita symbol(which is 1 for permutations ordered asijk,and −1 for permutations ordered askji).

Right versor

A unit vector in$\mathbb {R} ^{3}$was called aright versorbyW. R. Hamilton,as he developed hisquaternions$\mathbb {H} \subset \mathbb {R} ^{4}$.In fact, he was the originator of the termvector,as every quaternion$q=s+v$has a scalar partsand a vector partv.Ifvis a unit vector in$\mathbb {R} ^{3}$,then the square ofvin quaternions is –1. Thus byEuler's formula,$\exp(\theta v)=\cos \theta +v\sin \theta$is aversorin the3-sphere.Whenθis aright angle,the versor is a right versor: its scalar part is zero and its vector partvis a unit vector in$\mathbb {R} ^{3}$.

Thus the right versors extend the notion ofimaginary unitsfound in thecomplex plane,where the right versors now range over the2-sphere$\mathbb {S} ^{2}\subset \mathbb {R} ^{3}\subset \mathbb {H}$rather than the pair {i, –i} in the complex plane.

By extension, aright quaternionis a real multiple of a right versor.

See also

• Cartesian coordinate system
• Coordinate system
• Curvilinear coordinates
• Four-velocity
• Jacobian matrix and determinant
• Normal vector
• Polar coordinate system
• Standard basis
• Unit interval
• Unitsquare,cube,circle,sphere,andhyperbola
• Vector notation
• Vector of ones
• Unit matrix

References

• G. B. Arfken & H. J. Weber (2000).Mathematical Methods for Physicists(5th ed.). Academic Press.ISBN0-12-059825-6.
• Spiegel, Murray R. (1998).Schaum's Outlines: Mathematical Handbook of Formulas and Tables(2nd ed.). McGraw-Hill.ISBN0-07-038203-4.
• Griffiths, David J. (1998).Introduction to Electrodynamics(3rd ed.). Prentice Hall.ISBN0-13-805326-X.