Multiplication
This articleneeds additional citations forverification.(April 2012) |
| Arithmetic operations | ||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||





Multiplication(often denoted by thecross symbol×,by the mid-linedot operator⋅,byjuxtaposition,or, oncomputers,by anasterisk*) is one of the fourelementarymathematical operationsofarithmetic,with the other ones beingaddition,subtraction,anddivision.The result of a multiplication operation is called aproduct.
The multiplication ofwhole numbersmay be thought of asrepeated addition;that is, the multiplication of two numbers is equivalent to adding as many copies of one of them, themultiplicand,as the quantity of the other one, themultiplier;both numbers can be referred to asfactors.
For example, 4 multiplied by 3, often written asand spoken as "3 times 4", can be calculated by adding 3 copies of 4 together:
Here, 3 (themultiplier) and 4 (themultiplicand) are thefactors,and 12 is theproduct.
One of the mainpropertiesof multiplication is thecommutative property,which states in this case that adding 3 copies of 4 gives the same result as adding 4 copies of 3:
Thus, the designation of multiplier and multiplicand does not affect the result of the multiplication.[1]
Systematic generalizations of this basic definition define the multiplication of integers (including negative numbers), rational numbers (fractions), and real numbers.
Multiplication can also be visualized ascountingobjects arranged in arectangle(for whole numbers) or as finding theareaof a rectangle whose sides have some givenlengths.The area of a rectangle does not depend on which side is measured first—a consequence of the commutative property.
The product of two measurements (orphysical quantities) is a new type of measurement, usually with aderivedunit.For example, multiplying the lengths (in meters or feet) of the two sides of a rectangle gives its area (in square meters or square feet). Such a product is the subject ofdimensional analysis.
The inverse operation of multiplication isdivision.For example, since 4 multiplied by 3 equals 12, 12 divided by 3 equals 4. Indeed, multiplication by 3, followed by division by 3, yields the original number. The division of a number other than 0 by itself equals 1.
Several mathematical concepts expand upon the fundamental idea of multiplication. The product of a sequence,vector multiplication,complex numbers,andmatricesare all examples where this can be seen. These more advanced constructs tend to affect the basic properties in their own ways, such as becoming noncommutative in matrices and some forms of vector multiplication or changing thesignof complex numbers.
Notation[edit]
| × ⋅ | |
|---|---|
Multiplication signs | |
| InUnicode | U+00D7×MULTIPLICATION SIGN(×) U+22C5⋅DOT OPERATOR(⋅) |
| Different from | |
| Different from | U+00B7·MIDDLE DOT U+002E.FULL STOP |
Inarithmetic,multiplication is often written using themultiplication sign(either×or) between the terms (that is, ininfix notation).[2]For example,
- ( "two times threeequalssix ")
There are othermathematical notationsfor multiplication:
- To reduce confusion between the multiplication sign × and the common variablex,multiplication is also denoted by dot signs,[3]usually a middle-position dot (rarelyperiod):.
- The middle dot notation ordot operator,encoded in Unicode asU+22C5⋅DOT OPERATOR,is now standard in the United States and other countries where the period is used as adecimal point.When the dot operator character is not accessible, theinterpunct(·) is used. In other countries that use acommaas a decimal mark, either the period or a middle dot is used for multiplication.[citation needed]
- Historically, in the United Kingdom and Ireland, the middle dot was sometimes used for the decimal to prevent it from disappearing in the ruled line, and the period/full stop was used for multiplication. However, since theMinistry of Technologyruled to use the period as the decimal point in 1968,[4]and theInternational System of Units(SI) standard has since been widely adopted, this usage is now found only in the more traditional journals such asThe Lancet.[5]
- Inalgebra,multiplication involvingvariablesis often written as ajuxtaposition(e.g.,fortimesorfor five times), also calledimplied multiplication.[6]The notation can also be used for quantities that are surrounded byparentheses(e.g.,,orfor five times two). This implicit usage of multiplication can cause ambiguity when the concatenated variables happen to match the name of another variable, when a variable name in front of a parenthesis can be confused with a function name, or in the correct determination of theorder of operations.[7][8]
- Invector multiplication,there is a distinction between the cross and the dot symbols. The cross symbol generally denotes the taking across productof twovectors,yielding a vector as its result, while the dot denotes taking thedot productof two vectors, resulting in ascalar.
Incomputer programming,theasterisk(as in5*2) is still the most common notation. This is due to the fact that most computers historically were limited to smallcharacter sets(such asASCIIandEBCDIC) that lacked a multiplication sign (such as⋅or×), while the asterisk appeared on every keyboard.[citation needed]This usage originated in theFORTRANprogramming language.[9]
The numbers to be multiplied are generally called the "factors" (as infactorization). The number to be multiplied is the "multiplicand", and the number by which it is multiplied is the "multiplier". Usually, the multiplier is placed first, and the multiplicand is placed second;[1]however, sometimes the first factor is the multiplicand and the second the multiplier.[10] Also, as the result of multiplication does not depend on the order of the factors, the distinction between "multiplicand" and "multiplier" is useful only at a very elementary level and in somemultiplication algorithms,such as thelong multiplication.Therefore, in some sources, the term "multiplicand" is regarded as a synonym for "factor".[11] In algebra, a number that is the multiplier of a variable or expression (e.g., the 3 in) is called acoefficient.
The result of a multiplication is called aproduct.When one factor is an integer, the product is amultipleof the other or of the product of the others. Thus,is a multiple of,as is.A product of integers is a multiple of each factor; for example, 15 is the product of 3 and 5 and is both a multiple of 3 and a multiple of 5.
Definitions[edit]
This sectionneeds attention from an expert in Mathematics.The specific problem is:defining multiplication is not straightforward and different proposals have been made over the centuries, with competing ideas (e.g. recursive vs. non-recursive definitions).See thetalk pagefor details.(September 2023) |
The product of two numbers or the multiplication between two numbers can be defined for common special cases: natural numbers, integers, rational numbers, real numbers, complex numbers, and quaternions.
Product of two natural numbers[edit]
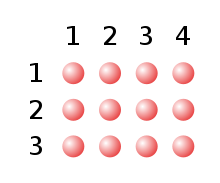
The product of two natural numbersis defined as:
Product of two integers[edit]
An integer can be either zero, a nonzero natural number, or minus a nonzero natural number. The product of zero and another integer is always zero. The product of two nonzero integers is determined by the product of theirpositive amounts,combined with the sign derived from the following rule:
(This rule is a consequence of thedistributivityof multiplication over addition, and is not anadditional rule.)
In words:
- A positive number multiplied by a positive number is positive (product of natural numbers),
- A positive number multiplied by a negative number is negative,
- A negative number multiplied by a positive number is negative,
- A negative number multiplied by a negative number is positive.
Product of two fractions[edit]
Two fractions can be multiplied by multiplying their numerators and denominators:
- which is defined when.
Product of two real numbers[edit]
There are several equivalent ways to define formally the real numbers; seeConstruction of the real numbers.The definition of multiplication is a part of all these definitions.
A fundamental aspect of these definitions is that every real number can be approximated to any accuracy byrational numbers.A standard way for expressing this is that every real number is theleast upper boundof a set of rational numbers. In particular, every positive real number is the least upper bound of thetruncationsof its infinitedecimal representation;for example,is the least upper bound of
A fundamental property of real numbers is that rational approximations are compatible witharithmetic operations,and, in particular, with multiplication. This means that, ifaandbare positive real numbers such thatandthenIn particular, the product of two positive real numbers is the least upper bound of the term-by-term products of thesequencesof their decimal representations.
As changing the signs transforms least upper bounds into greatest lower bounds, the simplest way to deal with a multiplication involving one or two negative numbers, is to use the rule of signs described above in§ Product of two integers.The construction of the real numbers throughCauchy sequencesis often preferred in order to avoid consideration of the four possible sign configurations.
Product of two complex numbers[edit]
Two complex numbers can be multiplied by the distributive law and the fact that,as follows:

Geometric meaning of complex multiplication can be understood rewriting complex numbers inpolar coordinates:
Furthermore,
from which one obtains
The geometric meaning is that the magnitudes are multiplied and the arguments are added.
Product of two quaternions[edit]
The product of twoquaternionscan be found in the article onquaternions.Note, in this case, thatandare in general different.
Computation[edit]

Many common methods for multiplying numbers using pencil and paper require amultiplication tableof memorized or consulted products of small numbers (typically any two numbers from 0 to 9). However, one method, thepeasant multiplicationalgorithm, does not. The example below illustrates "long multiplication" (the "standard algorithm", "grade-school multiplication" ):
23958233 × 5830 ——————————————— 00000000 ( = 23,958,233 × 0) 71874699 ( = 23,958,233 × 30) 191665864 ( = 23,958,233 × 800) + 119791165 ( = 23,958,233 × 5,000) ——————————————— 139676498390 ( = 139,676,498,390 )
In some countries such asGermany,the above multiplication is depicted similarly but with the original product kept horizontal and computation starting with the first digit of the multiplier:[12]
23958233 · 5830 ——————————————— 119791165 191665864 71874699 00000000 ——————————————— 139676498390
Multiplying numbers to more than a couple of decimal places by hand is tedious and error-prone.Common logarithmswere invented to simplify such calculations, since adding logarithms is equivalent to multiplying. Theslide ruleallowed numbers to be quickly multiplied to about three places of accuracy. Beginning in the early 20th century, mechanicalcalculators,such as theMarchant,automated multiplication of up to 10-digit numbers. Modern electroniccomputersand calculators have greatly reduced the need for multiplication by hand.
Historical algorithms[edit]
Methods of multiplication were documented in the writings ofancient Egyptian,Greek, Indian,[citation needed]andChinesecivilizations.
TheIshango bone,dated to about 18,000 to 20,000 BC, may hint at a knowledge of multiplication in theUpper Paleolithicera inCentral Africa,but this is speculative.[13][verification needed]
Egyptians[edit]
The Egyptian method of multiplication of integers and fractions, which is documented in theRhind Mathematical Papyrus,was by successive additions and doubling. For instance, to find the product of 13 and 21 one had to double 21 three times, obtaining2 × 21 = 42,4 × 21 = 2 × 42 = 84,8 × 21 = 2 × 84 = 168.The full product could then be found by adding the appropriate terms found in the doubling sequence:[14]
- 13 × 21 = (1 + 4 + 8) × 21 = (1 × 21) + (4 × 21) + (8 × 21) = 21 + 84 + 168 = 273.
Babylonians[edit]
TheBabyloniansused asexagesimalpositional number system,analogous to the modern-daydecimal system.Thus, Babylonian multiplication was very similar to modern decimal multiplication. Because of the relative difficulty of remembering60 × 60different products, Babylonian mathematicians employedmultiplication tables.These tables consisted of a list of the first twenty multiples of a certainprincipal numbern:n,2n,..., 20n;followed by the multiples of 10n:30n40n,and 50n.Then to compute any sexagesimal product, say 53n,one only needed to add 50nand 3ncomputed from the table.[citation needed]
Chinese[edit]

In the mathematical textZhoubi Suanjing,dated prior to 300 BC, and theNine Chapters on the Mathematical Art,multiplication calculations were written out in words, although the early Chinese mathematicians employedRod calculusinvolving place value addition, subtraction, multiplication, and division. The Chinese were already using adecimal multiplication tableby the end of theWarring Statesperiod.[15]
Modern methods[edit]

The modern method of multiplication based on theHindu–Arabic numeral systemwas first described byBrahmagupta.Brahmagupta gave rules for addition, subtraction, multiplication, and division.Henry Burchard Fine,then a professor of mathematics atPrinceton University,wrote the following:
- The Indians are the inventors not only of the positional decimal system itself, but of most of the processes involved in elementary reckoning with the system. Addition and subtraction they performed quite as they are performed nowadays; multiplication they effected in many ways, ours among them, but division they did cumbrously.[16]
These place value decimal arithmetic algorithms were introduced to Arab countries byAl Khwarizmiin the early 9th century and popularized in the Western world byFibonacciin the 13th century.[17]
Grid method[edit]
Grid method multiplication,or the box method, is used in primary schools in England and Wales and in some areas[which?]of the United States to help teach an understanding of how multiple digit multiplication works. An example of multiplying 34 by 13 would be to lay the numbers out in a grid as follows:
× 30 4 10 300 40 3 90 12
and then add the entries.
Computer algorithms[edit]
The classical method of multiplying twon-digit numbers requiresn2digit multiplications.Multiplication algorithmshave been designed that reduce the computation time considerably when multiplying large numbers. Methods based on thediscrete Fourier transformreduce thecomputational complexitytoO(nlognlog logn).In 2016, the factorlog lognwas replaced by a function that increases much slower, though still not constant.[18]In March 2019, David Harvey and Joris van der Hoeven submitted a paper presenting an integer multiplication algorithm with a complexity of[19]The algorithm, also based on the fast Fourier transform, is conjectured to be asymptotically optimal.[20]The algorithm is not practically useful, as it only becomes faster for multiplying extremely large numbers (having more than2172912bits).[21]
Products of measurements[edit]
One can only meaningfully add or subtract quantities of the same type, but quantities of different types can be multiplied or divided without problems. For example, four bags with three marbles each can be thought of as:[1]
- [4 bags] × [3 marbles per bag] = 12 marbles.
When two measurements are multiplied together, the product is of a type depending on the types of measurements. The general theory is given bydimensional analysis.This analysis is routinely applied in physics, but it also has applications in finance and other applied fields.
A common example in physics is the fact that multiplyingspeedbytimegivesdistance.For example:
- 50 kilometers per hour × 3 hours = 150 kilometers.
In this case, the hour units cancel out, leaving the product with only kilometer units.
Other examples of multiplication involving units include:
- 2.5 meters × 4.5 meters = 11.25 square meters
- 11 meters/seconds × 9 seconds = 99 meters
- 4.5 residents per house × 20 houses = 90 residents
Product of a sequence[edit]
Capital pi notation[edit]
The product of a sequence of factors can be written with the product symbol,which derives from the capital letter Π (pi) in theGreek Alpha bet(much like the same way thesummation symbolis derived from the Greek letter Σ (sigma)).[22][23]The meaning of this notation is given by
which results in
In such a notation, thevariableirepresents a varyinginteger,called the multiplication index, that runs from the lower value1indicated in the subscript to the upper value4given by the superscript. The product is obtained by multiplying together all factors obtained by substituting the multiplication index for an integer between the lower and the upper values (the bounds included) in the expression that follows the product operator.
More generally, the notation is defined as
wheremandnare integers or expressions that evaluate to integers. In the case wherem=n,the value of the product is the same as that of the single factorxm;ifm>n,the product is anempty productwhose value is 1—regardless of the expression for the factors.
Properties of capital pi notation[edit]
By definition,
If all factors are identical, a product ofnfactors is equivalent toexponentiation:
Associativityandcommutativityof multiplication imply
- and
ifais a non-negative integer, or if allare positivereal numbers,and
if allare non-negative integers, or ifxis a positive real number.
Infinite products[edit]
One may also consider products of infinitely many terms; these are calledinfinite products.Notationally, this consists in replacingnabove by theinfinity symbol∞. The product of such an infinite sequence is defined as thelimitof the product of the firstnterms, asngrows without bound. That is,
One can similarly replacemwith negative infinity, and define:
provided both limits exist.[citation needed]
Exponentiation[edit]
When multiplication is repeated, the resulting operation is known asexponentiation.For instance, the product of three factors of two (2×2×2) is "two raised to the third power", and is denoted by 23,a two with asuperscriptthree. In this example, the number two is thebase,and three is theexponent.[24]In general, the exponent (or superscript) indicates how many times the base appears in the expression, so that the expression
indicates thatncopies of the baseaare to be multiplied together. This notation can be used whenever multiplication is known to bepower associative.
Properties[edit]
Extension of this pattern into other quadrants gives the reason why a negative number times a negative number yields a positive number.
Note also how multiplication by zero causes a reduction in dimensionality, as does multiplication by asingular matrixwhere thedeterminantis 0. In this process, information is lost and cannot be regained.
Forrealandcomplexnumbers, which includes, for example,natural numbers,integers,andfractions,multiplication has certain properties:
- Commutative property
- The order in which two numbers are multiplied does not matter:[25][26]
- Associative property
- Expressions solely involving multiplication or addition are invariant with respect to theorder of operations:[25][26]
- Distributive property
- Holds with respect to multiplication over addition. This identity is of prime importance in simplifying algebraic expressions:[25][26]
- Identity element
- The multiplicative identity is 1; anything multiplied by 1 is itself. This feature of 1 is known as theidentity property:[25][26]
- Property of 0
- Any number multiplied by 0 is 0. This is known as thezero propertyof multiplication:[25]
- Negation
- −1 times any number is equal to theadditive inverseof that number:
- ,where
- −1 times −1 is 1:
- Inverse element
- Every numberx,except 0,has amultiplicative inverse,,such that.[27]
- Orderpreservation
- Multiplication by a positive number preserves theorder:
- Fora> 0,ifb>c,thenab>ac.
- Multiplication by a negative number reverses the order:
- Fora< 0,ifb>c,thenab<ac.
- Thecomplex numbersdo not have an ordering that is compatible with both addition and multiplication.[28]
Other mathematical systems that include a multiplication operation may not have all these properties. For example, multiplication is not, in general, commutative formatricesandquaternions.[25]
Axioms[edit]
In the bookArithmetices principia, nova methodo exposita,Giuseppe Peanoproposed axioms for arithmetic based on his axioms for natural numbers. Peano arithmetic has two axioms for multiplication:
HereS(y) represents thesuccessorofy;i.e., the natural number that followsy.The various properties like associativity can be proved from these and the other axioms of Peano arithmetic, includinginduction.For instance,S(0), denoted by 1, is a multiplicative identity because
The axioms forintegerstypically define them as equivalence classes of ordered pairs of natural numbers. The model is based on treating (x,y) as equivalent tox−ywhenxandyare treated as integers. Thus both (0,1) and (1,2) are equivalent to −1. The multiplication axiom for integers defined this way is
The rule that −1 × −1 = 1 can then be deduced from
Multiplication is extended in a similar way torational numbersand then toreal numbers.[citation needed]
Multiplication with set theory[edit]
The product of non-negative integers can be defined with set theory usingcardinal numbersor thePeano axioms.Seebelowhow to extend this to multiplying arbitrary integers, and then arbitrary rational numbers. The product of real numbers is defined in terms of products of rational numbers; seeconstruction of the real numbers.[29]
Multiplication in group theory[edit]
There are many sets that, under the operation of multiplication, satisfy the axioms that definegroupstructure. These axioms are closure, associativity, and the inclusion of an identity element and inverses.
A simple example is the set of non-zerorational numbers.Here identity 1 is had, as opposed to groups under addition where the identity is typically 0. Note that with the rationals, zero must be excluded because, under multiplication, it does not have an inverse: there is no rational number that can be multiplied by zero to result in 1. In this example, anabelian groupis had, but that is not always the case.
To see this, consider the set of invertible square matrices of a given dimension over a givenfield.Here, it is straightforward to verify closure, associativity, and inclusion of identity (theidentity matrix) and inverses. However, matrix multiplication is not commutative, which shows that this group is non-abelian.
Another fact worth noticing is that the integers under multiplication do not form a group—even if zero is excluded. This is easily seen by the nonexistence of an inverse for all elements other than 1 and −1.
Multiplication in group theory is typically notated either by a dot or by juxtaposition (the omission of an operation symbol between elements). So multiplying elementaby elementbcould be notated asaborab.When referring to a group via the indication of the set and operation, the dot is used. For example, our first example could be indicated by.[30]
Multiplication of different kinds of numbers[edit]
Numbers cancount(3 apples),order(the 3rd apple), ormeasure(3.5 feet high); as the history of mathematics has progressed from counting on our fingers to modelling quantum mechanics, multiplication has been generalized to more complicated and abstract types of numbers, and to things that are not numbers (such asmatrices) or do not look much like numbers (such asquaternions).
- Integers
- is the sum ofNcopies ofMwhenNandMare positive whole numbers. This gives the number of things in an arrayNwide andMhigh. Generalization to negative numbers can be done by
- and
- The same sign rules apply to rational and real numbers.
- Rational numbers
- Generalization to fractionsis by multiplying the numerators and denominators, respectively:.This gives the area of a rectanglehigh andwide, and is the same as the number of things in an array when the rational numbers happen to be whole numbers.[25]
- Real numbers
- Real numbers and their productscan be defined in terms of sequences of rational numbers.
- Complex numbers
- Considering complex numbersandas ordered pairs of real numbersand,the productis.This is the same as for realswhen theimaginary partsandare zero.
- Further generalizations
- SeeMultiplication in group theory,above, andmultiplicative group,which for example includes matrix multiplication. A very general, and abstract, concept of multiplication is as the "multiplicatively denoted" (second) binary operation in aring.An example of a ring that is not any of the above number systems is apolynomial ring(polynomials can be added and multiplied, but polynomials are not numbers in any usual sense).
- Division
- Often division,,is the same as multiplication by an inverse,.Multiplication for some types of "numbers" may have corresponding division, without inverses; in anintegral domainxmay have no inverse ""butmay be defined. In adivision ringthere are inverses, butmay be ambiguous in non-commutative rings sinceneed not be the same as.[citation needed]
See also[edit]
- Dimensional analysis
- Multiplication algorithm
- Karatsuba algorithm,for large numbers
- Toom–Cook multiplication,for very large numbers
- Schönhage–Strassen algorithm,for huge numbers
- Multiplication table
- Binary multiplier,how computers multiply
- Multiplicative inverse,reciprocal
- Factorial
- Genaille–Lucas rulers
- Lunar arithmetic
- Napier's bones
- Peasant multiplication
- Product (mathematics),for generalizations
- Slide rule
References[edit]
- ^abcDevlin, Keith(January 2011)."What Exactly is Multiplication?".Mathematical Association of America.Archivedfrom the original on 2017-05-27.Retrieved2017-05-14.
With multiplication you have a multiplicand (written second) multiplied by a multiplier (written first)
- ^Khan Academy (2015-08-14),Intro to multiplication | Multiplication and division | Arithmetic | Khan Academy,archivedfrom the original on 2017-03-24,retrieved2017-03-07
- ^Khan Academy (2012-09-06),Why aren't we using the multiplication sign? | Introduction to algebra | Algebra I | Khan Academy,archivedfrom the original on 2017-03-27,retrieved2017-03-07
- ^"Victory on Points".Nature.218(5137): 111. 1968.Bibcode:1968Natur.218S.111..doi:10.1038/218111c0.
- ^"The Lancet – Formatting guidelines for electronic submission of manuscripts"(PDF).Retrieved2017-04-25.
- ^Announcing the TI Programmable 88!(PDF).Texas Instruments.1982.Archived(PDF)from the original on 2017-08-03.Retrieved2017-08-03.
Now, implied multiplication is recognized by theAOSand the square root, logarithmic, and trigonometric functions can be followed by their arguments as when working with pencil and paper.
(NB. The TI-88 only existed as a prototype and was never released to the public.) - ^Peterson, Dave (2019-10-14)."Order of Operations: Implicit Multiplication?".Algebra / PEMDAS. The Math Doctors.Archivedfrom the original on 2023-09-24.Retrieved2023-09-25.
- ^Peterson, Dave (2023-08-18)."Implied Multiplication 1: Not as Bad as You Think".Algebra / Ambiguity, PEMDAS. The Math Doctors.Archivedfrom the original on 2023-09-24.Retrieved2023-09-25;Peterson, Dave (2023-08-25)."Implied Multiplication 2: Is There a Standard?".Algebra, Arithmetic / Ambiguity, PEMDAS. The Math Doctors.Archivedfrom the original on 2023-09-24.Retrieved2023-09-25;Peterson, Dave (2023-09-01)."Implied Multiplication 3: You Can't Prove It".Algebra / PEMDAS. The Math Doctors.Archivedfrom the original on 2023-09-24.Retrieved2023-09-25.
- ^Fuller, William R. (1977).FORTRAN Programming: A Supplement for Calculus Courses.Universitext. Springer. p. 10.doi:10.1007/978-1-4612-9938-7.ISBN978-0-387-90283-8.
- ^Ramone, Crewton."Multiplicand and Multiplier".Crewton Ramone's House of Math.Archivedfrom the original on 2015-10-26.Retrieved2015-11-10..
- ^Litvin, Chester (2012).Advance Brain Stimulation by Psychoconduction.Trafford. pp. 2–3, 5–6.ISBN978-1-4669-0152-0– viaGoogle Book Search.
- ^"Multiplication".mathematische-basteleien.de.Retrieved2022-03-15.
- ^Pletser, Vladimir (2012-04-04). "Does the Ishango Bone Indicate Knowledge of the Base 12? An Interpretation of a Prehistoric Discovery, the First Mathematical Tool of Humankind".arXiv:1204.1019[math.HO].
- ^"Peasant Multiplication".cut-the-knot.org.Retrieved2021-12-29.
- ^Qiu, Jane(2014-01-07)."Ancient times table hidden in Chinese bamboo strips".Nature.doi:10.1038/nature.2014.14482.S2CID130132289.Archivedfrom the original on 2014-01-22.Retrieved2014-01-22.
- ^Fine, Henry B.(1907).The Number System of Algebra – Treated Theoretically and Historically(PDF)(2nd ed.). p. 90.
- ^Bernhard, Adrienne."How modern mathematics emerged from a lost Islamic library".bbc.Retrieved2022-04-22.
- ^Harvey, David; van der Hoeven, Joris; Lecerf, Grégoire (2016). "Even faster integer multiplication".Journal of Complexity.36:1–30.arXiv:1407.3360.doi:10.1016/j.jco.2016.03.001.ISSN0885-064X.S2CID205861906.
- ^David Harvey, Joris Van Der Hoeven (2019).Integer multiplication in time O(n log n)Archived2019-04-08 at theWayback Machine
- ^Hartnett, Kevin (2019-04-11)."Mathematicians Discover the Perfect Way to Multiply".Quanta Magazine.Retrieved2020-01-25.
- ^Klarreich, Erica."Multiplication Hits the Speed Limit".cacm.acm.org.Archivedfrom the original on 2020-10-31.Retrieved2020-01-25.
- ^Weisstein, Eric W."Product".mathworld.wolfram.Retrieved2020-08-16.
- ^"Summation and Product Notation".math.illinoisstate.edu.Retrieved2020-08-16.
- ^Weisstein, Eric W."Exponentiation".mathworld.wolfram.Retrieved2021-12-29.
- ^abcdefghi"Multiplication".Encyclopedia of Mathematics.Retrieved2021-12-29.
- ^abcdBiggs, Norman L. (2002).Discrete Mathematics.Oxford University Press. p. 25.ISBN978-0-19-871369-2.
- ^Weisstein, Eric W."Multiplicative Inverse".Wolfram MathWorld.Retrieved2022-04-19.
- ^Angell, David."ORDERING COMPLEX NUMBERS... NOT*"(PDF).UNSW Sydney, School of Mathematics and Statistics.Retrieved2021-12-29.
- ^"10.2: Building the Real Numbers".Mathematics LibreTexts.2018-04-11.Retrieved2023-06-23.
- ^Burns, Gerald (1977).Introduction to group theory with applications.New York: Academic Press.ISBN9780121457501.
Further reading[edit]
- Boyer, Carl B.(revised byMerzbach, Uta C.) (1991).History of Mathematics.John Wiley and Sons, Inc.ISBN978-0-471-54397-8.
{{cite book}}:CS1 maint: multiple names: authors list (link)







![{\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\frac {\scriptstyle {\text{dividend}}}{\scriptstyle {\text{divisor}}}}\\[1ex]\scriptstyle {\frac {\scriptstyle {\text{numerator}}}{\scriptstyle {\text{denominator}}}}\end{matrix}}\right\}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d5d22ff59234f0d437be740306e8dd905991e1e)



![{\displaystyle \scriptstyle {\sqrt[{\text{degree}}]{\scriptstyle {\text{radicand}}}}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5582d567e7e7fbcdb728291770905e09beb0ea18)
































































































