E6(mathematics)

Inmathematics,E₆is the name of some closely relatedLie groups,linearalgebraic groupsor theirLie algebras${\mathfrak {e}}_{6}$,all of which have dimension 78; the same notation E₆is used for the correspondingroot lattice,which hasrank6. The designation E₆comes from the Cartan–Killing classification of the complexsimple Lie algebras(seeÉlie Cartan § Work). This classifies Lie algebras into four infinite series labeled A_n,B_n,C_n,D_n,andfive exceptional caseslabeled E₆,E₇,E₈,F₄,andG₂.The E₆algebra is thus one of the five exceptional cases.

The fundamental group of the complex form, compact real form, or any algebraic version of E₆is thecyclic groupZ/3Z,and itsouter automorphism groupis the cyclic groupZ/2Z.Itsfundamental representationis 27-dimensional (complex), and a basis is given by the27 lines on a cubic surface.Thedual representation,which is inequivalent, is also 27-dimensional.

Inparticle physics,E₆plays a role in somegrand unified theories.

Real and complex forms

There is a unique complex Lie algebra of type E₆,corresponding to a complex group of complex dimension 78. The complex adjoint Lie group E₆ofcomplex dimension78 can be considered as a simple real Lie group of real dimension 156. This has fundamental groupZ/3Z,has maximalcompactsubgroup the compact form (see below) of E₆,and has an outer automorphism group non-cyclic of order 4 generated by complex conjugation and by the outer automorphism which already exists as a complex automorphism.

As well as the complex Lie group of type E₆,there are five real forms of the Lie algebra, and correspondingly five real forms of the group with trivial center (all of which have an algebraic double cover, and three of which have further non-algebraic covers, giving further real forms), all of real dimension 78, as follows:

• The compact form (which is usually the one meant if no other information is given), which has fundamental groupZ/3Zand outer automorphism groupZ/2Z.
• The split form, EI (or E₆₍₆₎), which has maximal compact subgroup Sp(4)/(±1), fundamental group of order 2 and outer automorphism group of order 2.
• The quasi-split form EII (or E₆₍₂₎), which has maximal compact subgroup SU(2) × SU(6)/(center), fundamental group cyclic of order 6 and outer automorphism group of order 2.
• EIII (or E_6(-14)), which has maximal compact subgroup SO(2) × Spin(10)/(center), fundamental groupZand trivial outer automorphism group.
• EIV (or E_6(-26)), which has maximal compact subgroup F₄,trivial fundamental group cyclic and outer automorphism group of order 2.

The EIV form of E₆is the group of collineations (line-preserving transformations) of theoctonionic projective planeOP².It is also the group of determinant-preserving linear transformations of the exceptionalJordan algebra.The exceptional Jordan algebra is 27-dimensional, which explains why the compact real form of E₆has a 27-dimensional complex representation. The compact real form of E₆is theisometry groupof a 32-dimensionalRiemannian manifoldknown as the 'bioctonionic projective plane'; similar constructions for E₇and E₈are known as theRosenfeld projective planes,and are part of theFreudenthal magic square.

E₆as an algebraic group

By means of aChevalley basisfor the Lie algebra, one can define E₆as a linear algebraic group over the integers and, consequently, over any commutative ring and in particular over any field: this defines the so-called split (sometimes also known as "untwisted" ) adjoint form of E₆.Over an algebraically closed field, this and its triple cover are the only forms; however, over other fields, there are often many other forms, or "twists" of E₆,which are classified in the general framework ofGalois cohomology(over aperfect fieldk) by the setH¹(k,Aut(E₆)) which, because the Dynkin diagram of E₆(seebelow) has automorphism groupZ/2Z,maps toH¹(k,Z/2Z) = Hom (Gal(k),Z/2Z) with kernelH¹(k,E_6,ad).

Over the field of real numbers, the real component of the identity of these algebraically twisted forms of E₆coincide with the three real Lie groups mentionedabove,but with a subtlety concerning the fundamental group: all adjoint forms of E₆have fundamental groupZ/3Zin the sense of algebraic geometry, with Galois action as on the third roots of unity; this means that they admit exactly one triple cover (which may be trivial on the real points); the further non-compact real Lie group forms of E₆are therefore not algebraic and admit no faithful finite-dimensional representations. The compact real form of E₆as well as the noncompact forms EI=E₆₍₆₎and EIV=E_6(-26)are said to beinneror of type¹E₆meaning that their class lies inH¹(k,E_6,ad) or that complex conjugation induces the trivial automorphism on the Dynkin diagram, whereas the other two real forms are said to beouteror of type²E₆.

Over finite fields, theLang–Steinberg theoremimplies thatH¹(k,E₆) = 0, meaning that E₆has exactly one twisted form, known as²E₆:seebelow.

Automorphisms of an Albert Algebra

Similar to how the algebraic group G₂is the automorphism group of theoctonionsand the algebraic group F₄is the automorphism group of anAlbert algebra,an exceptionalJordan algebra,the algebraic group E₆is the group of linear automorphisms of an Albert algebra that preserve a certain cubic form, called the "determinant".

Algebra

Dynkin diagram

TheDynkin diagramfor E₆is given by,which may also be drawn as.

Roots of E₆

The 72 vertices of the1₂₂polytope represent the root vectors of the E₆,as shown in thisCoxeter planeprojection. Orange vertices are doubled in this projection.
Coxeter–Dynkin diagram:

Although theyspana six-dimensional space, it is much more symmetrical to consider them asvectorsin a six-dimensional subspace of a nine-dimensional space. Then one can take the roots to be

(1,−1,0;0,0,0;0,0,0), (−1,1,0;0,0,0;0,0,0),

(−1,0,1;0,0,0;0,0,0), (1,0,−1;0,0,0;0,0,0),

(0,1,−1;0,0,0;0,0,0), (0,−1,1;0,0,0;0,0,0),

(0,0,0;1,−1,0;0,0,0), (0,0,0;−1,1,0;0,0,0),

(0,0,0;−1,0,1;0,0,0), (0,0,0;1,0,−1;0,0,0),

(0,0,0;0,1,−1;0,0,0), (0,0,0;0,−1,1;0,0,0),

(0,0,0;0,0,0;1,−1,0), (0,0,0;0,0,0;−1,1,0),

(0,0,0;0,0,0;−1,0,1), (0,0,0;0,0,0;1,0,−1),

(0,0,0;0,0,0;0,1,−1), (0,0,0;0,0,0;0,−1,1),

plus all 27 combinations of$(\mathbf {3};\mathbf {3};\mathbf {3} )$where$\mathbf {3}$is one of$\left({\frac {2}{3}},-{\frac {1}{3}},-{\frac {1}{3}}\right),\ \left(-{\frac {1}{3}},{\frac {2}{3}},-{\frac {1}{3}}\right),\ \left(-{\frac {1}{3}},-{\frac {1}{3}},{\frac {2}{3}}\right),$ plus all 27 combinations of$({\bar {\mathbf {3} }};{\bar {\mathbf {3} }};{\bar {\mathbf {3} }})$where${\bar {\mathbf {3} }}$is one of$\left(-{\frac {2}{3}},{\frac {1}{3}},{\frac {1}{3}}\right),\ \left({\frac {1}{3}},-{\frac {2}{3}},{\frac {1}{3}}\right),\ \left({\frac {1}{3}},{\frac {1}{3}},-{\frac {2}{3}}\right).$

Simple roots

One possible selection for the simple roots of E₆is:

(0,0,0;0,0,0;0,1,−1)

(0,0,0;0,0,0;1,−1,0)

(0,0,0;0,1,−1;0,0,0)

(0,0,0;1,−1,0;0,0,0)

(0,1,−1;0,0,0;0,0,0)

$\left({\frac {1}{3}},-{\frac {2}{3}},{\frac {1}{3}};-{\frac {2}{3}},{\frac {1}{3}},{\frac {1}{3}};-{\frac {2}{3}},{\frac {1}{3}},{\frac {1}{3}}\right)$

Graph of E₆as a subgroup of E₈projected into the Coxeter plane

Hasse diagramof E₆root posetwith edge labels identifying added simple root position

E₆roots derived from the roots of E₈

E₆is the subset of E₈where a consistent set of three coordinates are equal (e.g. first or last). This facilitates explicit definitions of E₇and E₆as:

E₇= {α∈Z⁷∪ (Z+⁠1/2⁠)⁷:Σα_i²+α₁²= 2, Σα_i+α₁∈ 2Z},

E₆= {α∈Z⁶∪ (Z+⁠1/2⁠)⁶:Σα_i²+ 2α₁²= 2, Σα_i+ 2α₁∈ 2Z}

The following 72 E₆roots are derived in this manner from the split realeven E₈roots.Notice the last 3 dimensions being the same as required:

An alternative description

An alternative (6-dimensional) description of the root system, which is useful in considering E₆× SU(3) as asubgroup ofE₈,is the following:

All$4\times {\begin{pmatrix}5\\2\end{pmatrix}}$permutations of

$(\pm 1,\pm 1,0,0,0,0)$preserving the zero at the last entry,

and all of the following roots with an odd number of plus signs

$\left(\pm {1 \over 2},\pm {1 \over 2},\pm {1 \over 2},\pm {1 \over 2},\pm {1 \over 2},\pm {{\sqrt {3}} \over 2}\right).$

Thus the 78 generators consist of the following subalgebras:

A 45-dimensional SO(10) subalgebra, including the above$4\times {\begin{pmatrix}5\\2\end{pmatrix}}$generators plus the fiveCartan generatorscorresponding to the first five entries.

Two 16-dimensional subalgebras that transform as aWeyl spinorof$\operatorname {spin} (10)$and its complex conjugate. These have a non-zero last entry.

1 generator which is their chirality generator, and is the sixthCartan generator.

One choice ofsimple rootsfor E₆is given by the rows of the following matrix, indexed in the order:

$\left[{\begin{smallmatrix}1&-1&0&0&0&0\\0&1&-1&0&0&0\\0&0&1&-1&0&0\\0&0&0&1&1&0\\-{\frac {1}{2}}&-{\frac {1}{2}}&-{\frac {1}{2}}&-{\frac {1}{2}}&-{\frac {1}{2}}&{\frac {\sqrt {3}}{2}}\\0&0&0&1&-1&0\\\end{smallmatrix}}\right]$

Weyl group

TheWeyl groupof E₆is of order 51840: it is theautomorphismgroup of the uniquesimple groupof order 25920 (which can be described as any of: PSU₄(2), PSΩ₆⁻(2), PSp₄(3) or PSΩ₅(3)).

Cartan matrix

$\left[{\begin{smallmatrix}2&-1&0&0&0&0\\-1&2&-1&0&0&0\\0&-1&2&-1&0&-1\\0&0&-1&2&-1&0\\0&0&0&-1&2&0\\0&0&-1&0&0&2\end{smallmatrix}}\right]$

Important subalgebras and representations

Embeddings of the maximal subgroups of E₆up to dimension 78 with associated projection matrix.

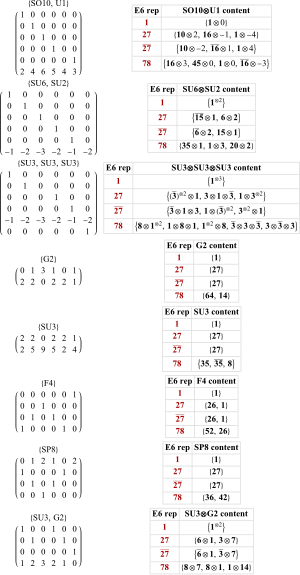
The Lie algebra E₆has an F₄subalgebra, which is the fixed subalgebra of an outer automorphism, and an SU(3) × SU(3) × SU(3) subalgebra. Other maximal subalgebras which have an importance in physics (see below) and can be read off the Dynkin diagram, are the algebras of SO(10) × U(1) and SU(6) × SU(2).

In addition to the 78-dimensional adjoint representation, there are two dual27-dimensional "vector" representations.

The characters of finite dimensional representations of the real and complex Lie algebras and Lie groups are all given by theWeyl character formula.The dimensions of the smallest irreducible representations are (sequenceA121737in theOEIS):

1,27 (twice),78,351 (four times),650,1728 (twice),2430,2925,3003 (twice),5824 (twice),7371 (twice), 7722 (twice), 17550 (twice), 19305 (four times), 34398 (twice),34749,43758,46332 (twice), 51975 (twice), 54054 (twice), 61425 (twice),70070,78975 (twice),85293,100386 (twice),105600,112320 (twice),146432 (twice),252252 (twice),314496 (twice), 359424 (four times),371800 (twice),386100 (twice), 393822 (twice), 412776 (twice),442442 (twice)...

The underlined terms in the sequence above are the dimensions of those irreducible representations possessed by the adjoint form of E₆(equivalently, those whose weights belong to the root lattice of E₆), whereas the full sequence gives the dimensions of the irreducible representations of the simply connected form of E₆.

The symmetry of the Dynkin diagram of E₆explains why many dimensions occur twice, the corresponding representations being related by the non-trivial outer automorphism; however, there are sometimes even more representations than this, such as four of dimension 351, two of which are fundamental and two of which are not.

Thefundamental representationshave dimensions 27, 351, 2925, 351, 27 and 78 (corresponding to the six nodes in theDynkin diagramin the order chosen for theCartan matrixabove, i.e., the nodes are read in the five-node chain first, with the last node being connected to the middle one).

The embeddings of the maximal subgroups of E₆up to dimension 78 are shown to the right.

E6 polytope

TheE₆polytopeis theconvex hullof the roots of E₆.It therefore exists in 6 dimensions; itssymmetry groupcontains theCoxeter groupfor E₆as anindex2 subgroup.

Chevalley and Steinberg groups of type E₆and²E₆

Main article:²E₆

The groups of typeE₆over arbitrary fields (in particular finite fields) were introduced by Dickson (1901,1908).

The points over afinite fieldwithqelements of the (split) algebraic group E₆(seeabove), whether of the adjoint (centerless) or simply connected form (its algebraic universal cover), give a finiteChevalley group.This is closely connected to the group written E₆(q), however there is ambiguity in this notation, which can stand for several things:

• the finite group consisting of the points overF_qof the simply connected form of E₆(for clarity, this can be written E_6,sc(q) or more rarely${\tilde {E}}_{6}(q)$and is known as the "universal" Chevalley group of type E₆overF_q),
• (rarely) the finite group consisting of the points overF_qof the adjoint form of E₆(for clarity, this can be written E_6,ad(q), and is known as the "adjoint" Chevalley group of type E₆overF_q), or
• the finite group which is the image of the natural map from the former to the latter: this is what will be denoted by E₆(q) in the following, as is most common in texts dealing with finite groups.

From the finite group perspective, the relation between these three groups, which is quite analogous to that between SL(n,q), PGL(n,q) and PSL(n,q), can be summarized as follows: E₆(q) is simple for anyq,E_6,sc(q) is itsSchur cover,and E_6,ad(q) lies in its automorphism group; furthermore, whenq−1 is not divisible by 3, all three coincide, and otherwise (whenqis congruent to 1 mod 3), the Schur multiplier of E₆(q) is 3 and E₆(q) is of index 3 in E_6,ad(q), which explains why E_6,sc(q) and E_6,ad(q) are often written as 3·E₆(q) and E₆(q)·3. From the algebraic group perspective, it is less common for E₆(q) to refer to the finite simple group, because the latter is not in a natural way the set of points of an algebraic group overF_qunlike E_6,sc(q) and E_6,ad(q).

Beyond this "split" (or "untwisted" ) form of E₆,there is also one other form of E₆over the finite fieldF_q,known as²E₆,which is obtained by twisting by the non-trivial automorphism of the Dynkin diagram of E₆.Concretely,²E₆(q), which is known as a Steinberg group, can be seen as the subgroup of E₆(q²) fixed by the composition of the non-trivial diagram automorphism and the non-trivial field automorphism ofF_q².Twisting does not change the fact that the algebraic fundamental group of²E_6,adisZ/3Z,but it does change thoseqfor which the covering of²E_6,adby²E_6,scis non-trivial on theF_q-points. Precisely:²E_6,sc(q) is a covering of²E₆(q), and²E_6,ad(q) lies in its automorphism group; whenq+1 is not divisible by 3, all three coincide, and otherwise (whenqis congruent to 2 mod 3), the degree of²E_6,sc(q) over²E₆(q) is 3 and²E₆(q) is of index 3 in²E_6,ad(q), which explains why²E_6,sc(q) and²E_6,ad(q) are often written as 3·²E₆(q) and²E₆(q)·3.

Two notational issues should be raised concerning the groups²E₆(q). One is that this is sometimes written²E₆(q²), a notation which has the advantage of transposing more easily to the Suzuki and Ree groups, but the disadvantage of deviating from the notation for theF_q-points of an algebraic group. Another is that whereas²E_6,sc(q) and²E_6,ad(q) are theF_q-points of an algebraic group, the group in question also depends onq(e.g., the points overF_q²of the same group are the untwisted E_6,sc(q²) and E_6,ad(q²)).

The groups E₆(q) and²E₆(q) are simple for anyq,and constitute two of the infinite families in theclassification of finite simple groups.Their order is given by the following formula (sequenceA008872in theOEIS):

$|E_{6}(q)|={\frac {1}{\mathrm {gcd} (3,q-1)}}q^{36}(q^{12}-1)(q^{9}-1)(q^{8}-1)(q^{6}-1)(q^{5}-1)(q^{2}-1)$

$|{}^{2}\!E_{6}(q)|={\frac {1}{\mathrm {gcd} (3,q+1)}}q^{36}(q^{12}-1)(q^{9}+1)(q^{8}-1)(q^{6}-1)(q^{5}+1)(q^{2}-1)$

(sequenceA008916in theOEIS). The order of E_6,sc(q) or E_6,ad(q) (both are equal) can be obtained by removing the dividing factor gcd(3,q−1) from the first formula (sequenceA008871in theOEIS), and the order of²E_6,sc(q) or²E_6,ad(q) (both are equal) can be obtained by removing the dividing factor gcd(3,q+1) from the second (sequenceA008915in theOEIS).

The Schur multiplier of E₆(q) is always gcd(3,q−1) (i.e., E_6,sc(q) is its Schur cover). The Schur multiplier of²E₆(q) is gcd(3,q+1) (i.e.,²E_6,sc(q) is its Schur cover) outside of the exceptional caseq=2 where it is 2²·3 (i.e., there is an additional 2²-fold cover). The outer automorphism group of E₆(q) is the product of the diagonal automorphism groupZ/gcd(3,q−1)Z(given by the action of E_6,ad(q)), the groupZ/2Zof diagram automorphisms, and the group of field automorphisms (i.e., cyclic of orderfifq=p^fwherepis prime). The outer automorphism group of²E₆(q) is the product of the diagonal automorphism groupZ/gcd(3,q+1)Z(given by the action of²E_6,ad(q)) and the group of field automorphisms (i.e., cyclic of orderfifq=p^fwherepis prime).

Importance in physics

The pattern ofweak isospin,W,weaker isospin,W′,strongg3andg8,and baryon minus lepton,B,charges for particles in theSO(10)Grand Unified Theory,rotated to show the embedding inE₆.

N= 8supergravityin five dimensions, which is adimensional reductionfromeleven-dimensional supergravity,admits anE₆bosonic global symmetry and anSp(8)bosoniclocal symmetry.The fermions are in representations ofSp(8),the gauge fields are in a representation ofE₆,and the scalars are in a representation of both (Gravitons aresingletswith respect to both). Physical states are in representations of the cosetE₆/Sp(8).

Ingrand unification theories,E₆appears as a possible gauge group which, after itsbreaking,gives rise tothe SU(3) × SU(2) × U(1)gauge groupof thestandard model.One way of achieving this is through breaking toSO(10)× U(1).The adjoint78representation breaks, as explained above, into an adjoint45,spinor16and16as well as a singlet of theSO(10)subalgebra. Including theU(1)charge we have

$78\rightarrow 45_{0}\oplus 16_{-3}\oplus {\overline {16}}_{3}+1_{0}.$

Where the subscript denotes theU(1)charge.

Likewise, the fundamental representation27and its conjugate27break into a scalar1,a vector10and a spinor, either16or16:

$27\rightarrow 1_{4}\oplus 10_{-2}\oplus 16_{1},$

${\bar {27}}\rightarrow 1_{-4}\oplus 10_{2}\oplus {\overline {16}}_{-1}.$

Thus, one can get the Standard Model's elementary fermions and Higgs boson.

See also

• En (Lie algebra)
• ADE classification
• Freudenthal magic square

References

• Adams, J. Frank (1996),Lectures on exceptional Lie groups,Chicago Lectures in Mathematics,University of Chicago Press,ISBN978-0-226-00526-3,MR1428422.
• Baez, John(2002)."The Octonions, Section 4.4: E₆".Bull. Amer. Math. Soc.39(2): 145–205.arXiv:math/0105155.doi:10.1090/S0273-0979-01-00934-X.ISSN0273-0979.S2CID586512.Online HTML version at[1].
• Cremmer, E.; J. Scherk; J. H. Schwarz (1979). "Spontaneously Broken N=8 Supergravity".Phys. Lett. B.84(1): 83–86.Bibcode:1979PhLB...84...83C.doi:10.1016/0370-2693(79)90654-3.Online scanned version at[2].
• Dickson, Leonard Eugene(1901),"A class of groups in an arbitrary realm connected with the configuration of the 27 lines on a cubic surface",The Quarterly Journal of Pure and Applied Mathematics,33:145–173, reprinted in volume V of his collected works
• Dickson, Leonard Eugene(1908),"A class of groups in an arbitrary realm connected with the configuration of the 27 lines on a cubic surface (second paper)",The Quarterly Journal of Pure and Applied Mathematics,39:205–209,ISBN9780828403061,reprinted in volume VI of his collected works
• Ichiro, Yokota (2009). "Exceptional Lie groups".arXiv:0902.0431[math.DG].