Riemann sphere

The Riemann sphere can be visualized as the complex number plane wrapped around a sphere (by some form ofstereographic projection– details are given below).

Stereographic projectionofcomplex numbers$A$and$B$onto the points$\ Alpha$and$\beta$of theRiemann sphere- connect$P(\infty )$with A or B by a line and determine the intersection with the sphere.

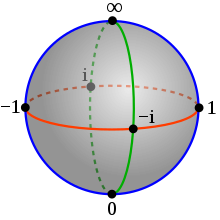
Inmathematics,theRiemann sphere,named afterBernhard Riemann, is amodelof theextended complex plane(also called theclosed complex plane): thecomplex planeplus onepoint at infinity.This extended plane represents theextended complex numbers,that is, thecomplex numbersplus a value$\infty$forinfinity.With the Riemann model, the point$\infty$is near to very large numbers, just as the point$0$is near to very small numbers.

The extended complex numbers are useful incomplex analysisbecause they allow fordivision by zeroin some circumstances, in a way that makes expressions such as$1/0=\infty$well-behaved.For example, anyrational functionon the complex plane can be extended to aholomorphic functionon the Riemann sphere, with thepolesof the rational function mapping to infinity. More generally, anymeromorphic functioncan be thought of as a holomorphic function whosecodomainis the Riemann sphere.

Ingeometry,the Riemann sphere is the prototypical example of aRiemann surface,and is one of the simplestcomplex manifolds.Inprojective geometry,the sphere is an example of acomplex projective spaceand can be thought of as thecomplexprojective line$\mathbf {P} ^{1}(\mathbf {C} )$,theprojective spaceof allcomplex linesin$\mathbf {C} ^{2}$.As with anycompactRiemann surface, the sphere may also be viewed as a projectivealgebraic curve,making it a fundamental example inalgebraic geometry.It also finds utility in other disciplines that depend on analysis and geometry, such as theBloch sphereofquantum mechanicsand in otherbranches of physics.

Extended complex numbers

Theextended complex numbersconsist of the complex numbers$\mathbf {C}$together with$\infty$.The set of extended complex numbers may be written as$\mathbf {C} \cup \{\infty \}$,and is often denoted by adding some decoration to the letter$\mathbf {C}$,such as

${\widehat {\mathbf {C} }},\quad {\overline {\mathbf {C} }},\quad {\text{or}}\quad \mathbf {C} _{\infty }.$

The notation$\mathbf {C} ^{*}$has also seen use, but as this notation is also used for the punctured plane$\mathbf {C} \setminus \{0\}$,it can lead to ambiguity.

Geometrically, the set of extended complex numbers is referred to as theRiemann sphere(orextended complex plane).

Arithmetic operations

Additionof complex numbers may be extended by defining, for$z\in \mathbf {C}$,

$z+\infty =\infty$

for any complex number$z$,andmultiplicationmay be defined by

$z\times \infty =\infty$

for all nonzero complex numbers$z$,with$\infty \times \infty =\infty$.Note that$\infty -\infty$and$0\times \infty$are leftundefined.Unlike the complex numbers, the extended complex numbers do not form afield,since$\infty$does not have anadditivenormultiplicative inverse.Nonetheless, it is customary to definedivisionon$\mathbf {C} \cup \{\infty \}$by

${\frac {z}{0}}=\infty \quad {\text{and}}\quad {\frac {z}{\infty }}=0$

for all nonzero complex numbers$z$with$\infty /0=\infty$and$0/\infty =0$.The quotients$0/0$and$\infty /\infty$are left undefined.

Rational functions

Anyrational function$f(z)=g(z)/h(z)$(in other words,$f(z)$is the ratio of polynomial functions$g(z)$and$h(z)$of$z$with complex coefficients, such that$g(z)$and$h(z)$have no common factor) can be extended to acontinuous functionon the Riemann sphere. Specifically, if$z_{0}$is a complex number such that the denominator$h(z_{0})$is zero but the numerator$g(z_{0})$is nonzero, then$f(z_{0})$can be defined as$\infty$.Moreover,$f(\infty )$can be defined as thelimitof$f(z)$as$z\to \infty$,which may be finite or infinite.

The set of complex rational functions—whose mathematical symbol is$\mathbf {C} (z)$—form all possibleholomorphic functionsfrom the Riemann sphere to itself, when it is viewed as aRiemann surface,except for the constant function taking the value$\infty$everywhere. The functions of$\mathbf {C} (z)$form an algebraic field, known asthe field of rational functions on the sphere.

For example, given the function

$f(z)={\frac {6z^{2}+1}{2z^{2}-50}}$

we may define$f(\pm 5)=\infty$,since the denominator is zero at$\pm 5$,and$f(\infty )=3$since$f(z)\to 3$as$z\to \infty$.Using these definitions,$f$becomes a continuous function from the Riemann sphere to itself.

As a complex manifold

As a one-dimensionalcomplex manifold,the Riemann sphere can be described by twocharts,both with domain equal to the complex number plane$\mathbf {C}$.Let$\zeta$be a complex number in one copy of$\mathbf {C}$,and let$\xi$be a complex number in another copy of$\mathbf {C}$.Identify each nonzero complex number$\zeta$of the first$\mathbf {C}$with the nonzero complex number$1/\xi$of the second$\mathbf {C}$.Then the map

$f(z)={\frac {1}{z}}$

is called thetransition mapbetween the two copies of$\mathbf {C}$—the so-called charts—glueing them together. Since the transition maps areholomorphic,they define a complex manifold, called theRiemann sphere.As a complex manifold of 1 complex dimension (i.e. 2 real dimensions), this is also called aRiemann surface.

Intuitively, the transition maps indicate how to glue two planes together to form the Riemann sphere. The planes are glued in an "inside-out" manner, so that they overlap almost everywhere, with each plane contributing just one point (its origin) missing from the other plane. In other words, (almost) every point in the Riemann sphere has both a$\zeta$value and a$\xi$value, and the two values are related by$\zeta =1/\xi$.The point where$\xi =0$should then have$\zeta$-value "$1/0$";in this sense, the origin of the$\xi$-chart plays the role of$\infty$in the$\zeta$-chart. Symmetrically, the origin of the$\zeta$-chart plays the role of$\infty$in the$\xi$-chart.

Topologically,the resulting space is theone-point compactificationof a plane into the sphere. However, the Riemann sphere is not merely a topological sphere. It is a sphere with a well-definedcomplex structure,so that around every point on the sphere there is a neighborhood that can bebiholomorphicallyidentified with$\mathbf {C}$.

On the other hand, theuniformization theorem,a central result in the classification of Riemann surfaces, states that everysimply-connectedRiemann surface is biholomorphic to the complex plane, thehyperbolic plane,or the Riemann sphere. Of these, the Riemann sphere is the only one that is aclosed surface(acompactsurface withoutboundary). Hence the two-dimensional sphere admits a unique complex structure turning it into a one-dimensional complex manifold.

As the complex projective line

The Riemann sphere can also be defined as thecomplex projective line.The points of the complex projective line can be defined asequivalence classesofnon-null vectorsin the complex vector space$\mathbf {C} ^{2}$:two non-null vectors$(w,z)$and$(u,v)$are equivalent iff$(w,z)=(\lambda u,\lambda v)$for some non-zero coefficient$\lambda \in \mathbf {C}$.

In this case, the equivalence class is written$[w,z]$usingprojective coordinates.Given any point$[w,z]$in the complex projective line, one of$w$and$z$must be non-zero, say$w\neq 0$.Then by the notion of equivalence,$[w,z]=\left[1,z/w\right]$,which is in a chart for the Riemann sphere manifold.

This treatment of the Riemann sphere connects most readily to projective geometry. For example, any line (or smooth conic) in thecomplex projective planeis biholomorphic to the complex projective line. It is also convenient for studying the sphere'sautomorphisms,later in this article.

As a sphere

Stereographic projection of a complex numberAonto a point α of the Riemann sphere.

The Riemann sphere can be visualized as the unit sphere$x^{2}+y^{2}+z^{2}=1$in the three-dimensional real space$\mathbf {R} ^{3}$.To this end, consider thestereographic projectionfrom the unit sphere minus the point$(0,0,1)$onto the plane$z=0,$which we identify with the complex plane by$\zeta =x+iy$.InCartesian coordinates$(x,y,z)$andspherical coordinates$(\theta,\varphi )$on the sphere (with$\theta$thezenithand$\varphi$theazimuth), the projection is

$\zeta ={\frac {x+iy}{1-z}}={\cot }{\bigl (}{\tfrac {1}{2}}\theta {\bigr )}\,e^{i\varphi }.$

Similarly, stereographic projection from$(0,0,-1)$onto the plane$z=0,$identified with another copy of the complex plane by$\xi =x-iy,$is written

$\xi ={\frac {x-iy}{1+z}}={\tan }{\bigl (}{\tfrac {1}{2}}\theta {\bigr )}\,e^{-i\varphi }.$

The inverses of these two stereographic projections are maps from the complex plane to the sphere. The first inverse covers the sphere except the point$(0,0,1)$,and the second covers the sphere except the point$(0,0,-1)$.The two complex planes, that are the domains of these maps, are identified differently with the plane$z=0$,because anorientation-reversal is necessary to maintain consistent orientation on the sphere.

The transition maps between$\zeta$-coordinates and$\xi$-coordinates are obtained by composing one projection with the inverse of the other. They turn out to be$\zeta =1/\xi$and$\xi =1/\zeta$,as described above. Thus the unit sphere isdiffeomorphicto the Riemann sphere.

Under this diffeomorphism, the unit circle in the$\zeta$-chart, the unit circle in the$\xi$-chart, and the equator of the unit sphere are all identified. The unit disk$|\zeta |<1$is identified with the southern hemisphere$z<0$,while the unit disk$|\xi |<1$is identified with the northern hemisphere$z>0$.

Metric

A Riemann surface does not come equipped with any particularRiemannian metric.The Riemann surface's conformal structure does, however, determine a class of metrics: all those whose subordinate conformal structure is the given one. In more detail: The complex structure of the Riemann surface does uniquely determine a metric up toconformal equivalence.(Two metrics are said to be conformally equivalent if they differ by multiplication by a positivesmooth function.) Conversely, any metric on anoriented surfaceuniquely determines a complex structure, which depends on the metric only up to conformal equivalence. Complex structures on an oriented surface are therefore in one-to-one correspondence with conformal classes of metrics on that surface.

Within a given conformal class, one can use conformal symmetry to find a representative metric with convenient properties. In particular, there is always a complete metric withconstant curvaturein any given conformal class.

In the case of the Riemann sphere, theGauss–Bonnet theoremimplies that a constant-curvature metric must have positivecurvature$K$.It follows that the metric must beisometricto the sphere of radius$1/{\sqrt {K}}$in$\mathbf {R} ^{3}$via stereographic projection. In the$\zeta$-chart on the Riemann sphere, the metric with$K=1$is given by

$ds^{2}=\left({\frac {2}{1+|\zeta |^{2}}}\right)^{2}\,|d\zeta |^{2}={\frac {4}{\left(1+\zeta {\overline {\zeta }}\right)^{2}}}\,d\zeta \,d{\overline {\zeta }}.$

In real coordinates$\zeta =u+iv$,the formula is

$ds^{2}={\frac {4}{\left(1+u^{2}+v^{2}\right)^{2}}}\left(du^{2}+dv^{2}\right).$

Up to a constant factor, this metric agrees with the standardFubini–Study metricon complex projective space (of which the Riemann sphere is an example).

Up to scaling, this is theonlymetric on the sphere whose group of orientation-preserving isometries is 3-dimensional (and none is more than 3-dimensional); that group is called${\mbox{SO}}(3)$.In this sense, this is by far the most symmetric metric on the sphere. (The group of all isometries, known as${\mbox{O}}(3)$,is also 3-dimensional, but unlike${\mbox{SO}}(3)$is not a connected space.)

Conversely, let$S$denote the sphere (as an abstractsmoothortopological manifold). By the uniformization theorem there exists a unique complex structure on$S$up to conformal equivalence. It follows that any metric on$S$is conformally equivalent to theround metric.All such metrics determine the same conformal geometry. The round metric is therefore not intrinsic to the Riemann sphere, since "roundness" is not an invariant of conformal geometry. The Riemann sphere is only aconformal manifold,not aRiemannian manifold.However, if one needs to do Riemannian geometry on the Riemann sphere, the round metric is a natural choice (with any fixed radius, though radius$1$is the simplest and most common choice). That is because only a round metric on the Riemann sphere has its isometry group be a 3-dimensional group. (Namely, the group known as${\mbox{SO}}(3)$,a continuous ( "Lie" ) group that is topologically the 3-dimensionalprojective space$\mathbf {P} ^{3}$.)

Automorphisms

AMöbius transformationacting on the sphere, and on the plane bystereographic projection.

Main article:Möbius transformation

The study of any mathematical object is aided by an understanding of itsgroupof automorphisms, meaning the maps from the object to itself that preserve the essential structure of the object. In the case of the Riemann sphere, an automorphism is an invertible conformal map (i.e. biholomorphic map) from the Riemann sphere to itself. It turns out that the only such maps are theMöbius transformations.These are functions of the form

$f(\zeta )={\frac {a\zeta +b}{c\zeta +d}},$

where$a$,$b$,$c$,and$d$are complex numbers such that$ad-bc\neq 0$.Examples of Möbius transformations includedilations,rotations,translations,and complex inversion. In fact, any Möbius transformation can be written as a composition of these.

The Möbius transformations arehomographieson the complex projective line. Inprojective coordinates,the transformationfcan be written

$[\zeta,\ 1]{\begin{pmatrix}a&c\\b&d\end{pmatrix}}\ =\ [a\zeta +b,\ c\zeta +d]\ =\ \left[{\tfrac {a\zeta +b}{c\zeta +d}},\ 1\right]\ =\ [f(\zeta ),\ 1].$

Thus the Möbius transformations can be described as two-by-two complex matrices with nonzerodeterminant.Since they act on projective coordinates, two matrices yield the same Möbius transformation if and only if they differ by a nonzero factor. Thegroupof Möbius transformations is theprojective linear group${\mbox{PGL}}(2,\mathbf {C} )$.

If one endows the Riemann sphere with theFubini–Study metric,then not all Möbius transformations are isometries; for example, the dilations and translations are not. The isometries form a proper subgroup of${\mbox{PGL}}(2,\mathbf {C} )$,namely${\mbox{PSU}}(2)$.This subgroup is isomorphic to therotation group${\mbox{SO}}(3)$,which is the group of symmetries of the unit sphere in$\mathbf {R} ^{3}$(which, when restricted to the sphere, become the isometries of the sphere).

Applications

In complex analysis, a meromorphic function on the complex plane (or on any Riemann surface, for that matter) is a ratio$f/g$of two holomorphic functions$f$and$g$.As a map to the complex numbers, it is undefined wherever$g$is zero. However, it induces a holomorphic map$(f,g)$to the complex projective line that is well-defined even where$g=0$.This construction is helpful in the study of holomorphic and meromorphic functions. For example, on a compact Riemann surface there are no non-constant holomorphic maps to the complex numbers, but holomorphic maps to the complex projective line are abundant.

The Riemann sphere has many uses in physics. In quantum mechanics, points on the complex projective line are natural values forphotonpolarizationstates,spinstates ofmassiveparticlesof spin$1/2$,and 2-state particles in general (see alsoQuantum bitandBloch sphere). The Riemann sphere has been suggested as arelativisticmodel for thecelestial sphere.Instring theory,theworldsheetsof strings are Riemann surfaces, and the Riemann sphere, being the simplest Riemann surface, plays a significant role. It is also important intwistor theory.

See also

• Conformal geometry
• Cross-ratio
• Dessin d'enfant
• Directed infinity
• Hopf bundle
• Möbius plane
• Parallel (operator) § Properties
• Projectively extended real line
• Smith chart
• Wheel theory

References

• Brown, James & Churchill, Ruel (1989).Complex Variables and Applications.New York: McGraw-Hill.ISBN0-07-010905-2.
• Goldman, William Mark (1999).Complex Hyperbolic Geometry.Oxford: New York: Oxford University Press.ISBN0-19-853793-X.
• Griffiths, Phillip & Harris, Joseph (1978).Principles of Algebraic Geometry.John Wiley & Sons.ISBN0-471-32792-1.
• Penrose, Roger (2007).The Road to Reality.London: National Geographic Books.ISBN978-0-679-77631-4.
• Riemann, Bernhard (1857)."Theorie der Abel'schen Functionen"[Theory of Abelian functions].Journal für die reine und angewandte Mathematik(in German).54:115–155.
• Rudin, Walter (1987).Real and Complex Analysis.New York: McGraw–Hill.ISBN0-07-100276-6.

External links

• "Riemann sphere",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• Moebius Transformations Revealed,byDouglas N. Arnoldand Jonathan Rogness (a video by two University of Minnesota professors explaining and illustrating Möbius transformations using stereographic projection from a sphere)