Exterior algebra

"Wedge product" redirects here. For the operation on topological spaces, seeWedge sum.

Orientation defined by an ordered set of vectors.

Reversed orientation corresponds to negating the exterior product.

Geometric interpretation of gradenelements in a real exterior algebra forn= 0(signed point), 1 (directed line segment, or vector), 2 (oriented plane element), 3 (oriented volume). The exterior product ofnvectors can be visualized as anyn-dimensional shape (e.g.n-parallelotope,n-ellipsoid); with magnitude (hypervolume), andorientationdefined by that of its(n− 1)-dimensional boundary and on which side the interior is.

In mathematics, theexterior algebraorGrassmann algebraof avector space$V$is anassociative algebrathat contains$V,$which has a product, calledexterior productorwedge productand denoted with$\wedge$,such that$v\wedge v=0$for every vector$v$in$V.$The exterior algebra is named afterHermann Grassmann,and the names of the product come from the "wedge" symbol$\wedge$and the fact that the product of two elements of$V$is "outside"$V.$

The wedge product of$k$vectors$v_{1}\wedge v_{2}\wedge \dots \wedge v_{k}$is called abladeofdegree$k$or$k$-blade.The wedge product was introduced originally as an algebraic construction used ingeometryto studyareas,volumes,and their higher-dimensional analogues: Themagnitudeof a2-blade$v\wedge w$is the area of theparallelogramdefined by$v$and$w,$and, more generally, the magnitude of a$k$-blade is the (hyper)volume of theparallelotopedefined by the constituent vectors. Thealternating propertythat$v\wedge v=0$implies a skew-symmetric property that$v\wedge w=-w\wedge v,$and more generally any blade flips sign whenever two of its constituent vectors are exchanged, corresponding to a parallelotope of opposite orientation.

The full exterior algebra contains objects that are not themselves blades, butlinear combinationsof blades; a sum of blades of homogeneous degree$k$is called ak-vector,while a more general sum of blades of arbitrary degree is called amultivector.Thelinear spanof the$k$-blades is called the$k$-th exterior powerof$V.$The exterior algebra is thedirect sumof the$k$-th exterior powers of$V,$and this makes the exterior algebra agraded algebra.

The exterior algebra isuniversalin the sense that every equation that relates elements of$V$in the exterior algebra is also valid in every associative algebra that contains$V$and in which the square of every element of$V$is zero.

The definition of the exterior algebra can be extended for spaces built from vector spaces, such asvector fieldsandfunctionswhosedomainis a vector space. Moreover, the field ofscalarsmay be any field (however for fields ofcharacteristictwo, the above condition$v\wedge v=0$must be replaced with$v\wedge w+w\wedge v=0,$which is equivalent in other characteristics). More generally, the exterior algebra can be defined formodulesover acommutative ring.In particular, the algebra ofdifferential formsin$k$variables is an exterior algebra over the ring of thesmooth functionsin$k$variables.

Motivating examples

Areas in the plane

The area of a parallelogram in terms of the determinant of the matrix of coordinates of two of its vertices.

The two-dimensionalEuclidean vector space$\mathbf {R} ^{2}$is arealvector space equipped with abasisconsisting of a pair of orthogonalunit vectors

${\mathbf {e} }_{1}={\begin{bmatrix}1\\0\end{bmatrix}},\quad {\mathbf {e} }_{2}={\begin{bmatrix}0\\1\end{bmatrix}}.$

Suppose that

$\mathbf {v} ={\begin{bmatrix}a\\b\end{bmatrix}}=a\mathbf {e} _{1}+b\mathbf {e} _{2},\quad \mathbf {w} ={\begin{bmatrix}c\\d\end{bmatrix}}=c\mathbf {e} _{1}+d\mathbf {e} _{2}$

are a pair of given vectors in⁠$\mathbf {R} ^{2}$⁠,written in components. There is a unique parallelogram having$\mathbf {v}$and$\mathbf {w}$as two of its sides. Theareaof this parallelogram is given by the standarddeterminantformula:

${\text{Area}}={\Bigl |}\det {\begin{bmatrix}\mathbf {v} &\mathbf {w} \end{bmatrix}}{\Bigr |}={\Biggl |}\det {\begin{bmatrix}a&c\\b&d\end{bmatrix}}{\Biggr |}=\left|ad-bc\right|.$

Consider now the exterior product of$\mathbf {v}$and⁠$\mathbf {w}$⁠:

${\begin{aligned}\mathbf {v} \wedge \mathbf {w} &=(a\mathbf {e} _{1}+b\mathbf {e} _{2})\wedge (c\mathbf {e} _{1}+d\mathbf {e} _{2})\\&=ac\mathbf {e} _{1}\wedge \mathbf {e} _{1}+ad\mathbf {e} _{1}\wedge \mathbf {e} _{2}+bc\mathbf {e} _{2}\wedge \mathbf {e} _{1}+bd\mathbf {e} _{2}\wedge \mathbf {e} _{2}\\&=\left(ad-bc\right)\mathbf {e} _{1}\wedge \mathbf {e} _{2}\end{aligned}}$

where the first step uses the distributive law for theexterior product,and the last uses the fact that the exterior product is analternating map,and in particular$\mathbf {e} _{2}\wedge \mathbf {e} _{1}=-(\mathbf {e} _{1}\wedge \mathbf {e} _{2}).$(The fact that the exterior product is an alternating map also forces$\mathbf {e} _{1}\wedge \mathbf {e} _{1}=\mathbf {e} _{2}\wedge \mathbf {e} _{2}=0.$) Note that the coefficient in this last expression is precisely the determinant of the matrix[vw].The fact that this may be positive or negative has the intuitive meaning thatvandwmay be oriented in a counterclockwise or clockwise sense as the vertices of the parallelogram they define. Such an area is called thesigned areaof the parallelogram: theabsolute valueof the signed area is the ordinary area, and the sign determines its orientation.

The fact that this coefficient is the signed area is not an accident. In fact, it is relatively easy to see that the exterior product should be related to the signed area if one tries to axiomatize this area as an algebraic construct. In detail, ifA(v,w)denotes the signed area of the parallelogram of which the pair of vectorsvandwform two adjacent sides, then A must satisfy the following properties:

1. A(rv,sw) =rsA(v,w)for any real numbersrands,since rescaling either of the sides rescales the area by the same amount (and reversing the direction of one of the sides reverses the orientation of the parallelogram).
2. A(v,v) = 0,since the area of thedegenerateparallelogram determined byv(i.e., aline segment) is zero.
3. A(w,v) = −A(v,w),since interchanging the roles ofvandwreverses the orientation of the parallelogram.
4. A(v+rw,w) = A(v,w)for any real numberr,since adding a multiple ofwtovaffects neither the base nor the height of the parallelogram and consequently preserves its area.
5. A(e₁,e₂) = 1,since the area of the unit square is one.

The cross product (bluevector) in relation to the exterior product (light blueparallelogram). The length of the cross product is to the length of the parallel unit vector (red) as the size of the exterior product is to the size of the reference parallelogram (light red).

With the exception of the last property, the exterior product of two vectors satisfies the same properties as the area. In a certain sense, the exterior product generalizes the final property by allowing the area of a parallelogram to be compared to that of any chosen parallelogram in a parallel plane (here, the one with sidese₁ande₂). In other words, the exterior product provides abasis-independentformulation of area.

Cross and triple products

For vectors inR³,the exterior algebra is closely related to thecross productandtriple product.Using the standard basis{e₁,e₂,e₃},the exterior product of a pair of vectors

$\mathbf {u} =u_{1}\mathbf {e} _{1}+u_{2}\mathbf {e} _{2}+u_{3}\mathbf {e} _{3}$

and

$\mathbf {v} =v_{1}\mathbf {e} _{1}+v_{2}\mathbf {e} _{2}+v_{3}\mathbf {e} _{3}$

is

$\mathbf {u} \wedge \mathbf {v} =(u_{1}v_{2}-u_{2}v_{1})(\mathbf {e} _{1}\wedge \mathbf {e} _{2})+(u_{3}v_{1}-u_{1}v_{3})(\mathbf {e} _{3}\wedge \mathbf {e} _{1})+(u_{2}v_{3}-u_{3}v_{2})(\mathbf {e} _{2}\wedge \mathbf {e} _{3})$

where {e₁∧e₂,e₃∧e₁,e₂∧e₃} is the basis for the three-dimensional space ⋀²(R³). The coefficients above are the same as those in the usual definition of thecross productof vectors in three dimensions, the only difference being that the exterior product is not an ordinary vector, but instead is abivector.

Bringing in a third vector

$\mathbf {w} =w_{1}\mathbf {e} _{1}+w_{2}\mathbf {e} _{2}+w_{3}\mathbf {e} _{3},$

the exterior product of three vectors is

$\mathbf {u} \wedge \mathbf {v} \wedge \mathbf {w} =(u_{1}v_{2}w_{3}+u_{2}v_{3}w_{1}+u_{3}v_{1}w_{2}-u_{1}v_{3}w_{2}-u_{2}v_{1}w_{3}-u_{3}v_{2}w_{1})(\mathbf {e} _{1}\wedge \mathbf {e} _{2}\wedge \mathbf {e} _{3})$

wheree₁∧e₂∧e₃is the basis vector for the one-dimensional space ⋀³(R³). The scalar coefficient is thetriple productof the three vectors.

The cross product and triple product in three dimensions each admit both geometric and algebraic interpretations. The cross productu×vcan be interpreted as a vector which is perpendicular to bothuandvand whose magnitude is equal to the area of the parallelogram determined by the two vectors. It can also be interpreted as the vector consisting of theminorsof the matrix with columnsuandv.The triple product ofu,v,andwis geometrically a (signed) volume. Algebraically, it is the determinant of the matrix with columnsu,v,andw.The exterior product in three dimensions allows for similar interpretations. In fact, in the presence of a positively orientedorthonormal basis,the exterior product generalizes these notions to higher dimensions.

Formal definition

The exterior algebra$\bigwedge (V)$of a vector space$V$over afield$K$is defined as thequotient algebraof thetensor algebraby the two-sidedideal$I$generated by all elements of the form$x\otimes x$such that$x\in V$.Symbolically,

$\bigwedge (V):=T(V)/I.\,$

The exterior product$\wedge$of two elements of$\bigwedge (V)$is defined by

$\ Alpha \wedge \beta =\ Alpha \otimes \beta {\pmod {I}}.$

Algebraic properties

Alternating product

The exterior product is by constructionalternatingon elements of⁠$V$⁠,which means that$x\wedge x=0$for all$x\in V,$by the above construction. It follows that the product is alsoanticommutativeon elements of⁠$V$⁠,for supposing that⁠$x,y\in V$⁠,

$0=(x+y)\wedge (x+y)=x\wedge x+x\wedge y+y\wedge x+y\wedge y=x\wedge y+y\wedge x$

hence

$x\wedge y=-(y\wedge x).$

More generally, if$\sigma$is apermutationof the integers⁠$[1,\dots,k]$⁠,and⁠$x_{1}$⁠,⁠$x_{2}$⁠,...,⁠$x_{k}$⁠are elements of⁠$V$⁠,it follows that

$x_{\sigma (1)}\wedge x_{\sigma (2)}\wedge \cdots \wedge x_{\sigma (k)}=\operatorname {sgn}(\sigma )x_{1}\wedge x_{2}\wedge \cdots \wedge x_{k},$

where$\operatorname {sgn}(\sigma )$is thesignature of the permutation⁠$\sigma$⁠.

In particular, if$x_{i}=x_{j}$for some⁠$i\neq j$⁠,then the following generalization of the alternating property also holds:

$x_{1}\wedge x_{2}\wedge \cdots \wedge x_{k}=0.$

Together with the distributive property of the exterior product, one further generalization is that a necessary and sufficient condition for$\{x_{1},x_{2},\dots,x_{k}\}$to be a linearly dependent set of vectors is that

$x_{1}\wedge x_{2}\wedge \cdots \wedge x_{k}=0.$

Exterior power

Thekthexterior powerof⁠$V$⁠,denoted⁠${\textstyle \bigwedge }^{\!k}(V)$⁠,is thevector subspaceof⁠${\textstyle \bigwedge }(V)$⁠spannedby elements of the form

$x_{1}\wedge x_{2}\wedge \cdots \wedge x_{k},\quad x_{i}\in V,i=1,2,\dots,k.$

If⁠$\ Alpha \in {\textstyle \bigwedge }^{\!k}(V)$⁠,then$\ Alpha$is said to be ak-vector.If, furthermore,$\ Alpha$can be expressed as an exterior product of$k$elements of⁠$V$⁠,then$\ Alpha$is said to bedecomposable(orsimple,by some authors; or ablade,by others). Although decomposable⁠$k$⁠-vectors span⁠${\textstyle \bigwedge }^{\!k}(V)$⁠,not every element of${\textstyle \bigwedge }^{\!k}(V)$is decomposable. For example, given⁠$\mathbf {R} ^{4}$⁠with a basis⁠$\{e_{1},e_{2},e_{3},e_{4}\}$⁠,the following 2-vector is not decomposable:

$\ Alpha =e_{1}\wedge e_{2}+e_{3}\wedge e_{4}.$

Basis and dimension

If thedimensionof$V$is$n$and$\{e_{1},\dots,e_{n}\}$is abasisfor$V$,then the set

$\{\,e_{i_{1}}\wedge e_{i_{2}}\wedge \cdots \wedge e_{i_{k}}~{\big |}~~1\leq i_{1}<i_{2}<\cdots <i_{k}\leq n\,\}$

is a basis for⁠${\textstyle \bigwedge }^{\!k}(V)$⁠.The reason is the following: given any exterior product of the form

$v_{1}\wedge \cdots \wedge v_{k},$

every vector$v_{j}$can be written as alinear combinationof the basis vectors⁠$e_{i}$⁠;using the bilinearity of the exterior product, this can be expanded to a linear combination of exterior products of those basis vectors. Any exterior product in which the same basis vector appears more than once is zero; any exterior product in which the basis vectors do not appear in the proper order can be reordered, changing the sign whenever two basis vectors change places. In general, the resulting coefficients of the basisk-vectors can be computed as theminorsof thematrixthat describes the vectors$v_{j}$in terms of the basis⁠$e_{i}$⁠.

By counting the basis elements, the dimension of${\textstyle \bigwedge }^{\!k}(V)$is equal to abinomial coefficient:

$\dim {\textstyle \bigwedge }^{\!k}(V)={\binom {n}{k}},$

where⁠$n$⁠is the dimension of thevectors,and⁠$k$⁠is the number of vectors in the product. The binomial coefficient produces the correct result, even for exceptional cases; in particular,${\textstyle \bigwedge }^{\!k}(V)=\{0\}$for⁠$k>n$⁠.

Any element of the exterior algebra can be written as a sum ofk-vectors.Hence, as a vector space the exterior algebra is adirect sum

${\textstyle \bigwedge }(V)={\textstyle \bigwedge }^{\!0}(V)\oplus {\textstyle \bigwedge }^{\!1}(V)\oplus {\textstyle \bigwedge }^{\!2}(V)\oplus \cdots \oplus {\textstyle \bigwedge }^{\!n}(V)$

(where, by convention,⁠${\textstyle \bigwedge }^{\!0}(V)=K$⁠,thefieldunderlying⁠$V$⁠,and⁠${\textstyle \bigwedge }^{\!1}(V)=V$⁠), and therefore its dimension is equal to the sum of the binomial coefficients, which is⁠$2^{n}$⁠.

Rank of ak-vector

If⁠$\ Alpha \in {\textstyle \bigwedge }^{\!k}(V)$⁠,then it is possible to express$\ Alpha$as a linear combination of decomposablek-vectors:

$\ Alpha =\ Alpha ^{(1)}+\ Alpha ^{(2)}+\cdots +\ Alpha ^{(s)}$

where each$\ Alpha ^{(i)}$is decomposable, say

$\ Alpha ^{(i)}=\ Alpha _{1}^{(i)}\wedge \cdots \wedge \ Alpha _{k}^{(i)},\quad i=1,2,\ldots,s.$

Therankof thek-vector$\ Alpha$is the minimal number of decomposablek-vectors in such an expansion of⁠$\ Alpha$⁠.This is similar to the notion oftensor rank.

Rank is particularly important in the study of 2-vectors (Sternberg 1964,§III.6) (Bryant et al. 1991). The rank of a 2-vector$\ Alpha$can be identified with half therank of the matrixof coefficients of$\ Alpha$in a basis. Thus if$e_{i}$is a basis for⁠$V$⁠,then$\ Alpha$can be expressed uniquely as

$\ Alpha =\sum _{i,j}a_{ij}e_{i}\wedge e_{j}$

where$a_{ij}=-a_{ji}$(the matrix of coefficients isskew-symmetric). The rank of the matrix$a_{ij}$is therefore even, and is twice the rank of the form$\ Alpha$.

In characteristic 0, the 2-vector$\ Alpha$has rank$p$if and only if

${\underset {p}{\underbrace {\ Alpha \wedge \cdots \wedge \ Alpha } }}\neq 0\$and$\ {\underset {p+1}{\underbrace {\ Alpha \wedge \cdots \wedge \ Alpha } }}=0.$

Graded structure

The exterior product of ak-vector with ap-vector is a$(k+p)$-vector, once again invoking bilinearity. As a consequence, the direct sum decomposition of the preceding section

${\textstyle \bigwedge }(V)={\textstyle \bigwedge }^{\!0}(V)\oplus {\textstyle \bigwedge }^{\!1}(V)\oplus {\textstyle \bigwedge }^{\!2}(V)\oplus \cdots \oplus {\textstyle \bigwedge }^{\!n}(V)$

gives the exterior algebra the additional structure of agraded algebra,that is

${\textstyle \bigwedge }^{\!k}(V)\wedge {\textstyle \bigwedge }^{\!p}(V)\subset {\textstyle \bigwedge }^{\!k+p}(V).$

Moreover, ifKis the base field, we have

${\textstyle \bigwedge }^{\!0}(V)=K$and${\textstyle \bigwedge }^{\!1}(V)=V.$

The exterior product is graded anticommutative, meaning that if$\ Alpha \in {\textstyle \bigwedge }^{\!k}(V)$and⁠$\beta \in {\textstyle \bigwedge }^{\!p}(V)$⁠,then

$\ Alpha \wedge \beta =(-1)^{kp}\beta \wedge \ Alpha.$

In addition to studying the graded structure on the exterior algebra,Bourbaki (1989)studies additional graded structures on exterior algebras, such as those on the exterior algebra of agraded module(a module that already carries its own gradation).

Universal property

LetVbe a vector space over the fieldK.Informally, multiplication in${\textstyle \bigwedge }(V)$is performed by manipulating symbols and imposing adistributive law,anassociative law,and using the identity$v\wedge v=0$forv∈V.Formally,${\textstyle \bigwedge }(V)$is the "most general" algebra in which these rules hold for the multiplication, in the sense that any unital associativeK-algebra containingVwith alternating multiplication onVmust contain a homomorphic image of⁠${\textstyle \bigwedge }(V)$⁠.In other words, the exterior algebra has the followinguniversal property:

Given any unital associativeK-algebraAand anyK-linear map$j:V\to A$such that$j(v)j(v)=0$for everyvinV,then there existsprecisely oneunitalalgebra homomorphism$f:{\textstyle \bigwedge }(V)\to A$such thatj(v) =f(i(v))for allvinV(hereiis the natural inclusion ofVin⁠${\textstyle \bigwedge }(V)$⁠,see above).

Universal property of the exterior algebra

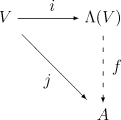
To construct the most general algebra that containsVand whose multiplication is alternating onV,it is natural to start with the most general associative algebra that containsV,thetensor algebraT(V),and then enforce the alternating property by taking a suitablequotient.We thus take the two-sidedidealIinT(V)generated by all elements of the formv⊗vforvinV,and define${\textstyle \bigwedge }(V)$as the quotient

${\textstyle \bigwedge }(V)=T(V)\,/\,I$

(and use∧as the symbol for multiplication in⁠${\textstyle \bigwedge }(V)$⁠). It is then straightforward to show that${\textstyle \bigwedge }(V)$containsVand satisfies the above universal property.

As a consequence of this construction, the operation of assigning to a vector spaceVits exterior algebra${\textstyle \bigwedge }(V)$is afunctorfrom thecategoryof vector spaces to the category of algebras.

Rather than defining${\textstyle \bigwedge }(V)$first and then identifying the exterior powers${\textstyle \bigwedge }^{\!k}(V)$as certain subspaces, one may alternatively define the spaces${\textstyle \bigwedge }^{\!k}(V)$first and then combine them to form the algebra⁠${\textstyle \bigwedge }(V)$⁠.This approach is often used in differential geometry and is described in the next section.

Generalizations

Given acommutative ring$R$and an$R$-module⁠$M$⁠,we can define the exterior algebra${\textstyle \bigwedge }(M)$just as above, as a suitable quotient of the tensor algebra⁠$\mathrm {T} (M)$⁠.It will satisfy the analogous universal property. Many of the properties of${\textstyle \bigwedge }(M)$also require that$M$be aprojective module.Where finite dimensionality is used, the properties further require that$M$befinitely generatedand projective. Generalizations to the most common situations can be found inBourbaki (1989).

Exterior algebras ofvector bundlesare frequently considered in geometry and topology. There are no essential differences between the algebraic properties of the exterior algebra of finite-dimensional vector bundles and those of the exterior algebra of finitely generated projective modules, by theSerre–Swan theorem.More general exterior algebras can be defined forsheavesof modules.

Alternating tensor algebra

For a field of characteristic not 2,the exterior algebra of a vector space$V$over$K$can be canonically identified with the vector subspace of$\mathrm {T} (V)$that consists ofantisymmetric tensors.For characteristic 0 (or higher than⁠$\dim V$⁠), the vector space of$k$-linear antisymmetric tensors is transversal to the ideal⁠$I$⁠,hence, a good choice to represent the quotient. But for nonzero characteristic, the vector space of⁠$K$⁠-linear antisymmetric tensors could be not transversal to the ideal (actually, for⁠$k\geq \operatorname {char} K$⁠,the vector space of$K$-linear antisymmetric tensors is contained in$I$); nevertheless, transversal or not, a product can be defined on this space such that the resulting algebra is isomorphic to the exterior algebra: in the first case the natural choice for the product is just the quotient product (using the available projection), in the second case, this product must be slightly modified as given below (along Arnold setting), but such that the algebra stays isomorphic with the exterior algebra, i.e. the quotient of$\mathrm {T} (V)$by the ideal$I$generated by elements of the form⁠$x\otimes x$⁠.Of course, for characteristic⁠$0$⁠(or higher than the dimension of the vector space), one or the other definition of the product could be used, as the two algebras are isomorphic (see V. I. Arnold or Kobayashi-Nomizu).

Let$\mathrm {T} ^{r}(V)$be the space of homogeneous tensors of degree$r$.This is spanned by decomposable tensors

$v_{1}\otimes \cdots \otimes v_{r},\quad v_{i}\in V.$

Theantisymmetrization(or sometimes theskew-symmetrization) of a decomposable tensor is defined by

$\operatorname {{\mathcal {A}}^{(r)}} (v_{1}\otimes \cdots \otimes v_{r})=\sum _{\sigma \in {\mathfrak {S}}_{r}}\operatorname {sgn} (\sigma )v_{\sigma (1)}\otimes \cdots \otimes v_{\sigma (r)}$

and, when$r!\neq 0$(for nonzero characteristic field$r!$might be 0):

$\operatorname {Alt} ^{(r)}(v_{1}\otimes \cdots \otimes v_{r})={\frac {1}{r!}}\operatorname {{\mathcal {A}}^{(r)}} (v_{1}\otimes \cdots \otimes v_{r})$

where the sum is taken over thesymmetric groupof permutations on the symbols⁠$\{1,\dots,r\}$⁠.This extends by linearity and homogeneity to an operation, also denoted by${\mathcal {A}}$and${\rm {Alt}}$,on the full tensor algebra⁠$\mathrm {T} (V)$⁠.

Note that

$\operatorname {{\mathcal {A}}^{(r)}} \operatorname {{\mathcal {A}}^{(r)}} =r!\operatorname {{\mathcal {A}}^{(r)}}.$

Such that, when defined,$\operatorname {Alt} ^{(r)}$is the projection for the exterior (quotient) algebra onto the r-homogeneous alternating tensor subspace. On the other hand, the image${\mathcal {A}}(\mathrm {T} (V))$is always thealternating tensor graded subspace(not yet an algebra, as product is not yet defined), denoted⁠$A(V)$⁠.This is a vector subspace of⁠$\mathrm {T} (V)$⁠,and it inherits the structure of a graded vector space from that on⁠$\mathrm {T} (V)$⁠.Moreover, the kernel of${\mathcal {A}}^{(r)}$is precisely⁠$I^{(r)}$⁠,the homogeneous subset of the ideal⁠$I$⁠,or the kernel of${\mathcal {A}}$is⁠$I$⁠.When$\operatorname {Alt}$is defined,$A(V)$carries an associative graded product${\widehat {\otimes }}$defined by (the same as the wedge product)

$t\wedge s=t~{\widehat {\otimes }}~s=\operatorname {Alt} (t\otimes s).$

Assuming$K$has characteristic 0, as$A(V)$is a supplement of$I$in⁠$\mathrm {T} (V)$⁠,with the above given product, there is a canonical isomorphism

$A(V)\cong {\textstyle \bigwedge }(V).$

When the characteristic of the field is nonzero,${\mathcal {A}}$will do what${\rm {Alt}}$did before, but the product cannot be defined as above. In such a case, isomorphism$A(V)\cong {\textstyle \bigwedge }(V)$still holds, in spite of$A(V)$not being a supplement of the ideal⁠$I$⁠,but then, the product should be modified as given below (${\dot {\wedge }}$product, Arnold setting).

Finally, we always get⁠$A(V)$⁠isomorphic with⁠${\textstyle \bigwedge }(V)$⁠,but the product could (or should) be chosen in two ways (or only one). Actually, the product could be chosen in many ways, rescaling it on homogeneous spaces as$c(r+p)/c(r)c(p)$for an arbitrary sequence$c(r)$in the field, as long as the division makes sense (this is such that the redefined product is also associative, i.e. defines an algebra on⁠$A(V)$⁠). Also note, the interior product definition should be changed accordingly, in order to keep its skew derivation property.

Index notation

Suppose thatVhas finite dimensionn,and that a basise₁,...,e_nofVis given. Then any alternating tensort∈ A^r(V) ⊂T^r(V)can be written inindex notationwith theEinstein summation conventionas

$t=t^{i_{1}i_{2}\cdots i_{r}}\,{\mathbf {e} }_{i_{1}}\otimes {\mathbf {e} }_{i_{2}}\otimes \cdots \otimes {\mathbf {e} }_{i_{r}},$

wheret^{i₁⋅⋅⋅i_r}iscompletely antisymmetricin its indices.

The exterior product of two alternating tensorstandsof ranksrandpis given by

$t~{\widehat {\otimes }}~s={\frac {1}{(r+p)!}}\sum _{\sigma \in {\mathfrak {S}}_{r+p}}\operatorname {sgn} (\sigma )t^{i_{\sigma (1)}\cdots i_{\sigma (r)}}s^{i_{\sigma (r+1)}\cdots i_{\sigma (r+p)}}{\mathbf {e} }_{i_{1}}\otimes {\mathbf {e} }_{i_{2}}\otimes \cdots \otimes {\mathbf {e} }_{i_{r+p}}.$

The components of this tensor are precisely the skew part of the components of the tensor products⊗t,denoted by square brackets on the indices:

$(t~{\widehat {\otimes }}~s)^{i_{1}\cdots i_{r+p}}=t^{[i_{1}\cdots i_{r}}s^{i_{r+1}\cdots i_{r+p}]}.$

Theinterior productmay also be described in index notation as follows. Let$t=t^{i_{0}i_{1}\cdots i_{r-1}}$be an antisymmetric tensor of rank⁠$r$⁠.Then, forα∈V^∗,⁠$\iota _{\ Alpha }t$⁠is an alternating tensor of rank⁠$r-1$⁠,given by

$(\iota _{\ Alpha }t)^{i_{1}\cdots i_{r-1}}=r\sum _{j=0}^{n}\ Alpha _{j}t^{ji_{1}\cdots i_{r-1}}.$

wherenis the dimension ofV.

Duality

Alternating operators

Given two vector spacesVandXand a natural numberk,analternating operatorfromV^ktoXis amultilinear map

$f:V^{k}\to X$

such that wheneverv₁,...,v_karelinearly dependentvectors inV,then

$f(v_{1},\ldots,v_{k})=0.$

The map

$w:V^{k}\to {\textstyle \bigwedge }^{\!k}(V),$

which associates to$k$vectors from$V$their exterior product, i.e. their corresponding$k$-vector, is also alternating. In fact, this map is the "most general" alternating operator defined on$V^{k};$given any other alternating operator$f:V^{k}\rightarrow X,$there exists a uniquelinear map$\phi:{\textstyle \bigwedge }^{\!k}(V)\rightarrow X$with$f=\phi \circ w.$Thisuniversal propertycharacterizes the space${\textstyle \bigwedge }^{\!k}(V)$and can serve as its definition.

Alternating multilinear forms

See also:Alternating multilinear map

Geometric interpretation for theexterior productofn1-forms(ε,η,ω) to obtain ann-form ( "mesh" ofcoordinate surfaces,here planes),forn= 1, 2, 3.The "circulations" showorientation.

The above discussion specializes to the case when⁠$X=K$⁠,the base field. In this case an alternating multilinear function

$f:V^{k}\to K$

is called analternating multilinear form.The set of allalternatingmultilinear formsis a vector space, as the sum of two such maps, or the product of such a map with a scalar, is again alternating. By the universal property of the exterior power, the space of alternating forms of degree$k$on$V$isnaturallyisomorphic with thedual vector space⁠${\bigl (}{\textstyle \bigwedge }^{\!k}(V){\bigr )}^{*}$⁠.If$V$is finite-dimensional, then the latter isnaturally isomorphicto⁠${\textstyle \bigwedge }^{\!k}\left(V^{*}\right)$⁠.In particular, if$V$is$n$-dimensional, the dimension of the space of alternating maps from$V^{k}$to$K$is thebinomial coefficient⁠$\textstyle {\binom {n}{k}}$⁠.

Under such identification, the exterior product takes a concrete form: it produces a new anti-symmetric map from two given ones. Supposeω:V^k→Kandη:V^m→Kare two anti-symmetric maps. As in the case oftensor productsof multilinear maps, the number of variables of their exterior product is the sum of the numbers of their variables. Depending on the choice of identification of elements of exterior power with multilinear forms, the exterior product is defined as

$\ Omega \wedge \eta =\operatorname {Alt} (\ Omega \otimes \eta )$

or as

$\ Omega {\dot {\wedge }}\eta ={\frac {(k+m)!}{k!\,m!}}\operatorname {Alt} (\ Omega \otimes \eta ),$

where, if the characteristic of the base field$K$is 0, the alternation Alt of a multilinear map is defined to be the average of the sign-adjusted values over all thepermutationsof its variables:

$\operatorname {Alt} (\ Omega )(x_{1},\ldots,x_{k})={\frac {1}{k!}}\sum _{\sigma \in S_{k}}\operatorname {sgn} (\sigma )\,\ Omega (x_{\sigma (1)},\ldots,x_{\sigma (k)}).$

When thefield$K$hasfinite characteristic,an equivalent version of the second expression without any factorials or any constants is well-defined:

${\ Omega {\dot {\wedge }}\eta (x_{1},\ldots,x_{k+m})}=\sum _{\sigma \in \mathrm {Sh} _{k,m}}\operatorname {sgn} (\sigma )\,\ Omega (x_{\sigma (1)},\ldots,x_{\sigma (k)})\,\eta (x_{\sigma (k+1)},\ldots,x_{\sigma (k+m)}),$

where hereSh_k,m⊂S_k+mis the subset of(k,m)shuffles:permutationsσof the set{1, 2,...,k+m}such thatσ(1) <σ(2) < ⋯ <σ(k),andσ(k+ 1) <σ(k+ 2) <... <σ(k+m).As this might look very specific and fine tuned, an equivalent raw version is to sum in the above formula over permutations in left cosets ofS_k+m/ (S_k×S_m).

Interior product

See also:Interior product

Suppose that$V$is finite-dimensional. If$V^{*}$denotes thedual spaceto the vector space⁠$V$⁠,then for each⁠$\ Alpha \in V^{*}$⁠,it is possible to define anantiderivationon the algebra⁠${\textstyle \bigwedge }(V)$⁠,

$\iota _{\ Alpha }:{\textstyle \bigwedge }^{\!k}(V)\rightarrow {\textstyle \bigwedge }^{\!k-1}(V).$

This derivation is called theinterior productwith⁠$\ Alpha$⁠,or sometimes theinsertion operator,orcontractionby⁠$\ Alpha$⁠.

Suppose that⁠$w\in {\textstyle \bigwedge }^{\!k}(V)$⁠.Then$w$is a multilinear mapping of$V^{*}$to⁠$K$⁠,so it is defined by its values on thek-foldCartesian product⁠$V^{*}\times V^{*}\times \dots \times V^{*}$⁠.Ifu₁,u₂,...,u_k−1are$k-1$elements of⁠$V^{*}$⁠,then define

$(\iota _{\ Alpha }w)(u_{1},u_{2},\ldots,u_{k-1})=w(\ Alpha,u_{1},u_{2},\ldots,u_{k-1}).$

Additionally, let$\iota _{\ Alpha }f=0$whenever$f$is a pure scalar (i.e., belonging to⁠${\textstyle \bigwedge }^{\!0}(V)$⁠).

Axiomatic characterization and properties

The interior product satisfies the following properties:

1. For each⁠$k$⁠and each⁠$\ Alpha \in V^{*}$⁠(where by convention$\Lambda ^{-1}(V)=\{0\}$),

   $\iota _{\ Alpha }:{\textstyle \bigwedge }^{\!k}(V)\rightarrow {\textstyle \bigwedge }^{\!k-1}(V).$

2. If$v$is an element of$V$(⁠$={\textstyle \bigwedge }^{\!1}(V)$⁠), then⁠$\iota _{\ Alpha }v=\ Alpha (v)$⁠is the dual pairing between elements of$V$and elements of⁠$V^{*}$⁠.
3. For each⁠$\ Alpha \in V^{*}$⁠,$\iota _{\ Alpha }$is agraded derivationof degree −1:

   $\iota _{\ Alpha }(a\wedge b)=(\iota _{\ Alpha }a)\wedge b+(-1)^{\deg a}a\wedge (\iota _{\ Alpha }b).$

These three properties are sufficient to characterize the interior product as well as define it in the general infinite-dimensional case.

Further properties of the interior product include:

• $\iota _{\ Alpha }\circ \iota _{\ Alpha }=0.$
• $\iota _{\ Alpha }\circ \iota _{\beta }=-\iota _{\beta }\circ \iota _{\ Alpha }.$

Hodge duality

Main article:Hodge star operator

Suppose that$V$has finite dimension⁠$n$⁠.Then the interior product induces a canonical isomorphism of vector spaces

${\textstyle \bigwedge }^{\!k}(V^{*})\otimes {\textstyle \bigwedge }^{\!n}(V)\to {\textstyle \bigwedge }^{\!n-k}(V)$

by the recursive definition

$\iota _{\ Alpha \wedge \beta }=\iota _{\beta }\circ \iota _{\ Alpha }.$

In the geometrical setting, a non-zero element of the top exterior power${\textstyle \bigwedge }^{\!n}(V)$(which is a one-dimensional vector space) is sometimes called avolume form(ororientation form,although this term may sometimes lead to ambiguity). The name orientation form comes from the fact that a choice of preferred top element determines an orientation of the whole exterior algebra, since it is tantamount to fi xing an ordered basis of the vector space. Relative to the preferred volume form⁠$\sigma$⁠,the isomorphism is given explicitly by

${\textstyle \bigwedge }^{\!k}(V^{*})\to {\textstyle \bigwedge }^{\!n-k}(V):\ Alpha \mapsto \iota _{\ Alpha }\sigma.$

If, in addition to a volume form, the vector spaceVis equipped with aninner productidentifying$V$with⁠$V^{*}$⁠,then the resulting isomorphism is called theHodge star operator,which maps an element to itsHodge dual:

$\star:{\textstyle \bigwedge }^{\!k}(V)\rightarrow {\textstyle \bigwedge }^{\!n-k}(V).$

The composition of$\star$with itself maps${\textstyle \bigwedge }^{\!k}(V)\to {\textstyle \bigwedge }^{\!k}(V)$and is always a scalar multiple of the identity map. In most applications, the volume form is compatible with the inner product in the sense that it is an exterior product of anorthonormal basisof⁠$V$⁠.In this case,

$\star \circ \star:{\textstyle \bigwedge }^{\!k}(V)\to {\textstyle \bigwedge }^{\!k}(V)=(-1)^{k(n-k)+q}\mathrm {id}$

where id is the identity mapping, and the inner product hasmetric signature(p,q)—ppluses andqminuses.

Inner product

For⁠$V$⁠a finite-dimensional space, aninner product(or apseudo-Euclideaninner product) on⁠$V$⁠defines an isomorphism of$V$with⁠$V^{*}$⁠,and so also an isomorphism of${\textstyle \bigwedge }^{\!k}(V)$with⁠${\bigl (}{\textstyle \bigwedge }^{\!k}V{\bigr )}^{*}$⁠.The pairing between these two spaces also takes the form of an inner product. On decomposable⁠$k$⁠-vectors,

$\left\langle v_{1}\wedge \cdots \wedge v_{k},w_{1}\wedge \cdots \wedge w_{k}\right\rangle =\det {\bigl (}\langle v_{i},w_{j}\rangle {\bigr )},$

the determinant of the matrix of inner products. In the special casev_i=w_i,the inner product is the square norm of thek-vector, given by the determinant of theGramian matrix(⟨v_i,v_j⟩).This is then extended bilinearly (or sesquilinearly in the complex case) to a non-degenerate inner product on${\textstyle \bigwedge }^{\!k}(V).$Ife_i,i= 1, 2,...,n,form anorthonormal basisof⁠$V$⁠,then the vectors of the form

$e_{i_{1}}\wedge \cdots \wedge e_{i_{k}},\quad i_{1}<\cdots <i_{k},$

constitute an orthonormal basis for⁠${\textstyle \bigwedge }^{\!k}(V)$⁠,a statement equivalent to theCauchy–Binet formula.

With respect to the inner product, exterior multiplication and the interior product are mutually adjoint. Specifically, for⁠$\mathbf {v} \in {\textstyle \bigwedge }^{\!k-1}(V)$⁠,⁠$\mathbf {w} \in {\textstyle \bigwedge }^{\!k}(V)$⁠,and⁠$x\in V$⁠,

$\langle x\wedge \mathbf {v},\mathbf {w} \rangle =\langle \mathbf {v},\iota _{x^{\flat }}\mathbf {w} \rangle$

wherex^♭∈V^∗is themusical isomorphism,the linear functional defined by

$x^{\flat }(y)=\langle x,y\rangle$

for all⁠$y\in V$⁠.This property completely characterizes the inner product on the exterior algebra.

Indeed, more generally for⁠$\mathbf {v} \in {\textstyle \bigwedge }^{\!k-l}(V)$⁠,⁠$\mathbf {w} \in {\textstyle \bigwedge }^{\!k}(V)$⁠,and⁠$\mathbf {x} \in {\textstyle \bigwedge }^{\!l}(V)$⁠,iteration of the above adjoint properties gives

$\langle \mathbf {x} \wedge \mathbf {v},\mathbf {w} \rangle =\langle \mathbf {v},\iota _{\mathbf {x} ^{\flat }}\mathbf {w} \rangle$

where now$\mathbf {x} ^{\flat }\in {\textstyle \bigwedge }^{\!l}\left(V^{*}\right)\simeq {\bigl (}{\textstyle \bigwedge }^{\!l}(V){\bigr )}^{*}$is the dual⁠$l$⁠-vector defined by

$\mathbf {x} ^{\flat }(\mathbf {y} )=\langle \mathbf {x},\mathbf {y} \rangle$

for all⁠$\mathbf {y} \in {\textstyle \bigwedge }^{\!l}(V)$⁠.

Bialgebra structure

There is a correspondence between the graded dual of the graded algebra${\textstyle \bigwedge }(V)$and alternating multilinear forms on⁠$V$⁠.The exterior algebra (as well as thesymmetric algebra) inherits a bialgebra structure, and, indeed, aHopf algebrastructure, from thetensor algebra.See the article ontensor algebrasfor a detailed treatment of the topic.

The exterior product of multilinear forms defined above is dual to acoproductdefined on⁠${\textstyle \bigwedge }(V)$⁠,giving the structure of acoalgebra.Thecoproductis a linear function⁠$\Delta:{\textstyle \bigwedge }(V)\to {\textstyle \bigwedge }(V)\otimes {\textstyle \bigwedge }(V)$⁠,which is given by

$\Delta (v)=1\otimes v+v\otimes 1$

on elements⁠$v\in V$⁠.The symbol$1$stands for the unit element of the field⁠$K$⁠.Recall that⁠$K\simeq {\textstyle \bigwedge }^{\!0}(V)\subseteq {\textstyle \bigwedge }(V)$⁠,so that the above really does lie in⁠${\textstyle \bigwedge }(V)\otimes {\textstyle \bigwedge }(V)$⁠.This definition of the coproduct is lifted to the full space${\textstyle \bigwedge }(V)$by (linear) homomorphism. The correct form of this homomorphism is not what one might naively write, but has to be the one carefully defined in thecoalgebraarticle. In this case, one obtains

$\Delta (v\wedge w)=1\otimes (v\wedge w)+v\otimes w-w\otimes v+(v\wedge w)\otimes 1.$

Expanding this out in detail, one obtains the following expression on decomposable elements:

$\Delta (x_{1}\wedge \cdots \wedge x_{k})=\sum _{p=0}^{k}\;\sum _{\sigma \in Sh(p,k-p)}\;\operatorname {sgn} (\sigma )(x_{\sigma (1)}\wedge \cdots \wedge x_{\sigma (p)})\otimes (x_{\sigma (p+1)}\wedge \cdots \wedge x_{\sigma (k)}).$

where the second summation is taken over all(p,k−p)-shuffles.By convention, one takes that Sh(k,0) and Sh(0,k) equals {id: {1,...,k} → {1,...,k}}. It is also convenient to take the pure wedge products$v_{\sigma (1)}\wedge \dots \wedge v_{\sigma (p)}$and$v_{\sigma (p+1)}\wedge \dots \wedge v_{\sigma (k)}$ to equal 1 forp= 0 andp=k,respectively (the empty product in${\textstyle \bigwedge }(V)$). The shuffle follows directly from the first axiom of a co-algebra: the relative order of the elements$x_{k}$ispreservedin the riffle shuffle: the riffle shuffle merely splits the ordered sequence into two ordered sequences, one on the left, and one on the right.

Observe that the coproduct preserves the grading of the algebra. Extending to the full space${\textstyle {\textstyle \bigwedge }(V),}$one has

$\Delta:{\textstyle \bigwedge }^{k}(V)\to \bigoplus _{p=0}^{k}{\textstyle \bigwedge }^{p}(V)\otimes {\textstyle \bigwedge }^{k-p}(V)$

The tensor symbol ⊗ used in this section should be understood with some caution: it isnotthe same tensor symbol as the one being used in the definition of the alternating product. Intuitively, it is perhaps easiest to think it as just another, but different, tensor product: it is still (bi-)linear, as tensor products should be, but it is the product that is appropriate for the definition of a bialgebra, that is, for creating the object⁠${\textstyle \bigwedge }(V)\otimes {\textstyle \bigwedge }(V)$⁠.Any lingering doubt can be shaken by pondering the equalities(1 ⊗v) ∧ (1 ⊗w) = 1 ⊗ (v∧w)and(v⊗ 1) ∧ (1 ⊗w) =v⊗w,which follow from the definition of the coalgebra, as opposed to naive manipulations involving the tensor and wedge symbols. This distinction is developed in greater detail in the article ontensor algebras.Here, there is much less of a problem, in that the alternating product$\wedge$clearly corresponds to multiplication in the exterior algebra, leaving the symbol$\otimes$free for use in the definition of the bialgebra. In practice, this presents no particular problem, as long as one avoids the fatal trap of replacing alternating sums of$\otimes$by the wedge symbol, with one exception. One can construct an alternating product from⁠$\otimes$⁠,with the understanding that it works in a different space. Immediately below, an example is given: the alternating product for thedual spacecan be given in terms of the coproduct. The construction of the bialgebra here parallels the construction in thetensor algebraarticle almost exactly, except for the need to correctly track the alternating signs for the exterior algebra.

In terms of the coproduct, the exterior product on the dual space is just the graded dual of the coproduct:

$(\ Alpha \wedge \beta )(x_{1}\wedge \cdots \wedge x_{k})=(\ Alpha \otimes \beta )\left(\Delta (x_{1}\wedge \cdots \wedge x_{k})\right)$

where the tensor product on the right-hand side is of multilinear linear maps (extended by zero on elements of incompatible homogeneous degree: more precisely,α∧β=ε∘ (α⊗β) ∘ Δ,where$\varepsilon$is the counit, as defined presently).

Thecounitis the homomorphism$\varepsilon:{\textstyle \bigwedge }(V)\to K$that returns the 0-graded component of its argument. The coproduct and counit, along with the exterior product, define the structure of abialgebraon the exterior algebra.

With anantipodedefined on homogeneous elements by⁠$S(x)=(-1)^{\binom {{\text{deg}}\,x\,+1}{2}}x$⁠,the exterior algebra is furthermore aHopf algebra.

Functoriality

Suppose that$V$and$W$are a pair of vector spaces and$f:V\to W$is alinear map.Then, by the universal property, there exists a unique homomorphism of graded algebras

${\textstyle \bigwedge }(f):{\textstyle \bigwedge }(V)\rightarrow {\textstyle \bigwedge }(W)$

such that

${\textstyle \bigwedge }(f)\left|_{{\textstyle \bigwedge }^{\!1}(V)}\right.=f:V={\textstyle \bigwedge }^{\!1}(V)\rightarrow W={\textstyle \bigwedge }^{\!1}(W).$

In particular,${\textstyle \bigwedge }(f)$preserves homogeneous degree. Thek-graded components of${\textstyle \bigwedge \left(f\right)}$are given on decomposable elements by

${\textstyle \bigwedge }(f)(x_{1}\wedge \cdots \wedge x_{k})=f(x_{1})\wedge \cdots \wedge f(x_{k}).$

Let

${\textstyle \bigwedge }^{\!k}(f)={\textstyle \bigwedge }(f)\left|_{{\textstyle \bigwedge }^{\!k}(V)}\right.:{\textstyle \bigwedge }^{\!k}(V)\rightarrow {\textstyle \bigwedge }^{\!k}(W).$

The components of the transformation⁠${\textstyle \bigwedge }^{\!k}(f)$⁠relative to a basis of$V$and$W$is the matrix of$k\times k$minors of⁠$f$⁠.In particular, if$V=W$and$V$is of finite dimension⁠$n$⁠,then${\textstyle \bigwedge }^{\!n}(f)$is a mapping of a one-dimensional vector space${\textstyle \bigwedge }^{\!n}(V)$to itself, and is therefore given by a scalar: thedeterminantof⁠$f$⁠.

Exactness

If$0\to U\to V\to W\to 0$is ashort exact sequenceof vector spaces, then

$0\to {\textstyle \bigwedge }^{\!1}(U)\wedge {\textstyle \bigwedge }(V)\to {\textstyle \bigwedge }(V)\to {\textstyle \bigwedge }(W)\to 0$

is an exact sequence of graded vector spaces,as is

$0\to {\textstyle \bigwedge }(U)\to {\textstyle \bigwedge }(V).$

Direct sums

In particular, the exterior algebra of a direct sum is isomorphic to the tensor product of the exterior algebras:

${\textstyle \bigwedge }(V\oplus W)\cong {\textstyle \bigwedge }(V)\otimes {\textstyle \bigwedge }(W).$

This is a graded isomorphism; i.e.,

${\textstyle \bigwedge }^{\!k}(V\oplus W)\cong \bigoplus _{p+q=k}{\textstyle \bigwedge }^{\!p}(V)\otimes {\textstyle \bigwedge }^{\!q}(W).$

In greater generality, for a short exact sequence of vector spaces${\textstyle 0\to U\mathrel {\overset {f}{\to }} V\mathrel {\overset {g}{\to }} W\to 0,}$there is a naturalfiltration

$0=F^{0}\subseteq F^{1}\subseteq \cdots \subseteq F^{k}\subseteq F^{k+1}={\textstyle \bigwedge }^{\!k}(V)$

where$F^{p}$for$p\geq 1$is spanned by elements of the form$u_{1}\wedge \ldots \wedge u_{k+1-p}\wedge v_{1}\wedge \ldots v_{p-1}$for$u_{i}\in U$and$v_{i}\in V.$ The corresponding quotients admit a natural isomorphism

$F^{p+1}/F^{p}\cong {\textstyle \bigwedge }^{\!k-p}(U)\otimes {\textstyle \bigwedge }^{\!p}(W)$given by$u_{1}\wedge \ldots \wedge u_{k-p}\wedge v_{1}\wedge \ldots \wedge v_{p}\mapsto u_{1}\wedge \ldots \wedge u_{k-p}\otimes g(v_{1})\wedge \ldots \wedge g(v_{p}).$

In particular, ifUis 1-dimensional then

$0\to U\otimes {\textstyle \bigwedge }^{\!k-1}(W)\to {\textstyle \bigwedge }^{\!k}(V)\to {\textstyle \bigwedge }^{\!k}(W)\to 0$

is exact, and ifWis 1-dimensional then

$0\to {\textstyle \bigwedge }^{k}(U)\to {\textstyle \bigwedge }^{\!k}(V)\to {\textstyle \bigwedge }^{\!k-1}(U)\otimes W\to 0$

is exact.

Applications

Oriented volume in affine space

The natural setting for (oriented)$k$-dimensional volume and exterior algebra isaffine space.This is also the intimate connection between exterior algebra anddifferential forms,as to integrate we need a 'differential' object to measure infinitesimal volume. If$\mathbb {A}$is an affine space over the vector space⁠$V$⁠,and a (simplex) collection of ordered$k+1$points$A_{0},A_{1},...,A_{k}$,we can define its oriented$k$-dimensional volume as the exterior product of vectors$A_{0}A_{1}\wedge A_{0}A_{2}\wedge \cdots \wedge A_{0}A_{k}={}$$(-1)^{j}A_{j}A_{0}\wedge A_{j}A_{1}\wedge A_{j}A_{2}\wedge \cdots \wedge A_{j}A_{k}$(using concatenation$PQ$to mean thedisplacement vectorfrom point$P$to$Q$); if the order of the points is changed, the oriented volume changes by a sign, according to the parity of the permutation. In⁠$n$⁠-dimensional space, the volume of any$n$-dimensional simplex is a scalar multiple of any other.

The sum of the$(k-1)$-dimensional oriented areas of the boundary simplexes of a⁠$k$⁠-dimensional simplex is zero, as for the sum of vectors around a triangle or the oriented triangles bounding the tetrahedron in the previous section.

The vector space structure on${\textstyle \bigwedge }(V)$generalises addition of vectors in⁠$V$⁠:we have$(u_{1}+u_{2})\wedge v=u_{1}\wedge v+u_{2}\wedge v$and similarly ak-blade$v_{1}\wedge \dots \wedge v_{k}$is linear in each factor.

Linear algebra

In applications tolinear algebra,the exterior product provides an abstract algebraic manner for describing thedeterminantand theminorsof amatrix.For instance, it is well known that the determinant of a square matrix is equal to the volume of the parallelotope whose sides are the columns of the matrix (with a sign to track orientation). This suggests that the determinant can bedefinedin terms of the exterior product of the column vectors. Likewise, thek×kminors of a matrix can be defined by looking at the exterior products of column vectors chosenkat a time. These ideas can be extended not just to matrices but tolinear transformationsas well: the determinant of a linear transformation is the factor by which it scales the oriented volume of any given reference parallelotope. So the determinant of a linear transformation can be defined in terms of what the transformation does to the top exterior power. The action of a transformation on the lesser exterior powers gives abasis-independent way to talk about the minors of the transformation.

Physics

Main article:Electromagnetic tensor

In physics, many quantities are naturally represented by alternating operators. For example, if the motion of a charged particle is described by velocity and acceleration vectors in four-dimensional spacetime, then normalization of the velocity vector requires that the electromagnetic force must be an alternating operator on the velocity. Its six degrees of freedom are identified with the electric and magnetic fields.

Electromagnetic field

InEinstein's theories of relativity,theelectromagnetic fieldis generally given as adifferential 2-form$F=dA$in4-spaceor as the equivalentalternating tensor field$F_{ij}=A_{[i,j]}=A_{[i;j]},$theelectromagnetic tensor.Then$dF=ddA=0$or the equivalent Bianchi identity$F_{[ij,k]}=F_{[ij;k]}=0.$ None of this requires a metric.

Adding theLorentz metricand anorientationprovides theHodge star operator$\star$and thus makes it possible to define$J={\star }d{\star }F$or the equivalent tensordivergence$J^{i}=F_{,j}^{ij}=F_{;j}^{ij}$where$F^{ij}=g^{ik}g^{jl}F_{kl}.$

Linear geometry

The decomposablek-vectors have geometric interpretations: the bivector$u\wedge v$represents the plane spanned by the vectors, "weighted" with a number, given by the area of the orientedparallelogramwith sides$u$and⁠$v$⁠.Analogously, the 3-vector$u\wedge v\wedge w$represents the spanned 3-space weighted by the volume of the orientedparallelepipedwith edges⁠$u$⁠,⁠$v$⁠,and⁠$w$⁠.

Projective geometry

Decomposablek-vectors in${\textstyle \bigwedge }^{\!k}(V)$correspond to weightedk-dimensionallinear subspacesof⁠$V$⁠.In particular, theGrassmannianofk-dimensional subspaces of⁠$V$⁠,denoted⁠$\operatorname {Gr} _{k}(V)$⁠,can be naturally identified with analgebraic subvarietyof theprojective space${\textstyle \mathbf {P} {\bigl (}{\textstyle \bigwedge }^{\!k}(V){\bigr )}}$.This is called thePlücker embedding,and the image of the embedding can be characterized by thePlücker relations.

Differential geometry

The exterior algebra has notable applications indifferential geometry,where it is used to definedifferential forms.Differential forms are mathematical objects that evaluate the length of vectors, areas of parallelograms, and volumes ofhigher-dimensional bodies,so they can beintegratedover curves, surfaces and higher dimensionalmanifoldsin a way that generalizes theline integralsandsurface integralsfrom calculus. Adifferential format a point of adifferentiable manifoldis an alternating multilinear form on thetangent spaceat the point. Equivalently, a differential form of degreekis alinear functionalon thekth exterior power of the tangent space. As a consequence, the exterior product of multilinear forms defines a natural exterior product for differential forms. Differential forms play a major role in diverse areas of differential geometry.

Analternate approachdefines differential forms in terms ofgerms of functions.

In particular, theexterior derivativegives the exterior algebra of differential forms on a manifold the structure of adifferential graded algebra.The exterior derivative commutes withpullbackalong smooth mappings between manifolds, and it is therefore anaturaldifferential operator.The exterior algebra of differential forms, equipped with the exterior derivative, is acochain complexwhose cohomology is called thede Rham cohomologyof the underlying manifold and plays a vital role in thealgebraic topologyof differentiable manifolds.

Representation theory

Inrepresentation theory,the exterior algebra is one of the two fundamentalSchur functorson the category of vector spaces, the other being thesymmetric algebra.Together, these constructions are used to generate theirreducible representationsof thegeneral linear group(seeFundamental representation).

Superspace

The exterior algebra over the complex numbers is the archetypal example of asuperalgebra,which plays a fundamental role in physical theories pertaining tofermionsandsupersymmetry.A single element of the exterior algebra is called asupernumberorGrassmann number.The exterior algebra itself is then just a one-dimensionalsuperspace:it is just the set of all of the points in the exterior algebra. The topology on this space is essentially theweak topology,theopen setsbeing thecylinder sets.Ann-dimensional superspace is just the⁠$n$⁠-fold product of exterior algebras.

Lie algebra homology

Let$L$be a Lie algebra over a field⁠$K$⁠,then it is possible to define the structure of achain complexon the exterior algebra of⁠$L$⁠.This is a⁠$K$⁠-linear mapping

$\partial:{\textstyle \bigwedge }^{\!p+1}(L)\to {\textstyle \bigwedge }^{\!p}(L)$

defined on decomposable elements by

$\partial (x_{1}\wedge \cdots \wedge x_{p+1})={\frac {1}{p+1}}\sum _{j<\ell }(-1)^{j+\ell +1}[x_{j},x_{\ell }]\wedge x_{1}\wedge \cdots \wedge {\hat {x}}_{j}\wedge \cdots \wedge {\hat {x}}_{\ell }\wedge \cdots \wedge x_{p+1}.$

TheJacobi identityholds if and only if⁠${1}$⁠,and so this is a necessary and sufficient condition for an anticommutative nonassociative algebra$L$to be a Lie algebra. Moreover, in that case${\textstyle {\textstyle \bigwedge }(L)}$is achain complexwith boundary operator⁠$\partial$⁠.Thehomologyassociated to this complex is theLie algebra homology.

Homological algebra

The exterior algebra is the main ingredient in the construction of theKoszul complex,a fundamental object inhomological algebra.

History

The exterior algebra was first introduced byHermann Grassmannin 1844 under the blanket term ofAusdehnungslehre,orTheory of Extension. This referred more generally to an algebraic (or axiomatic) theory of extended quantities and was one of the early precursors to the modern notion of avector space.Saint-Venantalso published similar ideas of exterior calculus for which he claimed priority over Grassmann.

The algebra itself was built from a set of rules, or axioms, capturing the formal aspects of Cayley and Sylvester's theory of multivectors. It was thus acalculus,much like thepropositional calculus,except focused exclusively on the task of formal reasoning in geometrical terms. In particular, this new development allowed for anaxiomaticcharacterization of dimension, a property that had previously only been examined from the coordinate point of view.

The import of this new theory of vectors andmultivectorswas lost to mid-19th-century mathematicians, until being thoroughly vetted byGiuseppe Peanoin 1888. Peano's work also remained somewhat obscure until the turn of the century, when the subject was unified by members of the French geometry school (notablyHenri Poincaré,Élie Cartan,andGaston Darboux) who applied Grassmann's ideas to the calculus ofdifferential forms.

A short while later,Alfred North Whitehead,borrowing from the ideas of Peano and Grassmann, introduced hisuniversal algebra.This then paved the way for the 20th-century developments ofabstract algebraby placing the axiomatic notion of an algebraic system on a firm logical footing.

See also

• Alternating algebra
• Exterior calculus identities
• Clifford algebra,a generalization of exterior algebra to a nonzeroquadratic form
• Geometric algebra
• Koszul complex
• Multilinear algebra
• Symmetric algebra,the symmetric analog
• Tensor algebra
• Weyl algebra,aquantum deformationof the symmetric algebra by asymplectic form

References

Mathematical references

• Bishop, R.;Goldberg, S.I. (1980),Tensor analysis on manifolds,Dover,ISBN0-486-64039-6

  Includes a treatment of alternating tensors and alternating forms, as well as a detailed discussion of Hodge duality from the perspective adopted in this article.

• Bourbaki, Nicolas(1989),Elements of mathematics, Algebra I,Springer-Verlag,ISBN3-540-64243-9

  This is themain mathematical referencefor the article. It introduces the exterior algebra of a module over a commutative ring (although this article specializes primarily to the case when the ring is a field), including a discussion of the universal property, functoriality, duality, and the bialgebra structure. See §III.7 and §III.11.

• Bryant, R.L.;Chern, S.S.;Gardner, R.B.; Goldschmidt, H.L.;Griffiths, P.A.(1991),Exterior differential systems,Springer-Verlag

  This book contains applications of exterior algebras to problems inpartial differential equations.Rank and related concepts are developed in the early chapters.

• Mac Lane, S.;Birkhoff, G.(1999),Algebra,AMS Chelsea,ISBN0-8218-1646-2

  Chapter XVI sections 6–10 give a more elementary account of the exterior algebra, including duality, determinants and minors, and alternating forms.

• Sternberg, Shlomo(1964),Lectures on Differential Geometry,Prentice Hall

  Contains a classical treatment of the exterior algebra as alternating tensors, and applications to differential geometry.

Historical references

• Bourbaki (1989,Historical note on chapters II and III)
• Clifford, W.(1878), "Applications of Grassmann's Extensive Algebra",American Journal of Mathematics,1(4), The Johns Hopkins University Press: 350–358,doi:10.2307/2369379,JSTOR2369379
• Forder, H.G.(1941),The Calculus of Extension,Internet Archive
• Grassmann, Hermann(1844),Die Lineale Ausdehnungslehre – Ein neuer Zweig der Mathematik(in German)(The Linear Extension Theory – A new Branch of Mathematics)alternative reference
• Kannenberg, Lloyd (2000),Extension Theory (translation of Grassmann'sAusdehnungslehre),American Mathematical Society,ISBN0-8218-2031-1
• Peano, Giuseppe(1888),Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva;Kannenberg, Lloyd (1999),Geometric calculus: According to the Ausdehnungslehre of H. Grassmann,Birkhäuser,ISBN978-0-8176-4126-9.
• Whitehead, Alfred North(1898),"A Treatise on Universal Algebra, with Applications",Nature,58(1504), Cambridge: 385,Bibcode:1898Natur..58..385G,doi:10.1038/058385a0,S2CID3985954

Other references and further reading

• Browne, J.M. (2007),Grassmann algebra – Exploring applications of Extended Vector Algebra with Mathematica,archived fromthe originalon 2009-02-19,retrieved2007-05-09

  An introduction to the exterior algebra, andgeometric algebra,with a focus on applications. Also includes a history section and bibliography.

• Spivak, Michael(1965),Calculus on manifolds,Addison-Wesley,ISBN978-0-8053-9021-6

  Includes applications of the exterior algebra to differential forms, specifically focused onintegrationandStokes's theorem.The notation${\textstyle {\textstyle \bigwedge }^{\!k}V}$in this text is used to mean the space of alternatingk-forms onV;i.e., for Spivak${\textstyle {\textstyle \bigwedge }^{\!k}V}$is what this article would call${\textstyle {\textstyle \bigwedge }^{\!k}V^{*}.}$Spivak discusses this in Addendum 4.

• Strang, G.(1993),Introduction to linear algebra,Wellesley-Cambridge Press,ISBN978-0-9614088-5-5

  Includes an elementary treatment of the axiomatization of determinants as signed areas, volumes, and higher-dimensional volumes.

• Onishchik, A.L. (2001) [1994],"Exterior algebra",Encyclopedia of Mathematics,EMS Press
• Wendell, Fleming (2012) [1977],"7. Exterior algebra and differential calculus",Functions of Several Variables(2nd ed.), Springer, pp. 275–320,ISBN978-1-4684-9461-7

  This textbook inmultivariate calculusintroduces the exterior algebra of differential forms adroitly into the calculus sequence for colleges.

• Shafarevich, I.R.;Remizov, A.O. (2012).Linear Algebra and Geometry.Springer.ISBN978-3-642-30993-9.

  Chapter 10: The Exterior Product and Exterior Algebras

• "The Grassmann method in projective geometry"A compilation of English translations of three notes by Cesare Burali-Forti on the application of exterior algebra to projective geometry
• C. Burali-Forti, "Introduction to Differential Geometry, following the method of H. Grassmann"An English translation of an early book on the geometric applications of exterior algebras
• "Mechanics, according to the principles of the theory of extension"An English translation of one Grassmann's papers on the applications of exterior algebra