Four-dimensional space

The 4D equivalent of acubeis known as atesseract,seen rotating here in four-dimensional space, yet projected into two dimensions for display.

Four-dimensional space(4D) is the mathematical extension of the concept ofthree-dimensional space(3D). Three-dimensional space is the simplest possible abstraction of the observation that one needs only three numbers, calleddimensions,to describe thesizesorlocationsof objects in the everyday world. For example, thevolumeof a rectangular box is found by measuring and multiplying its length, width, and height (often labeledx,y,andz). This concept of ordinary space is calledEuclidean spacebecause it corresponds toEuclid's geometry,which was originally abstracted from the spatial experiences of everyday life.

The idea of adding a fourth dimension appears inJean le Rond d'Alembert's "Dimensions", published in 1754,but the mathematics of more than three dimensions onlyemerged in the 19th century.The general concept ofEuclidean spacewith any number of dimensions was fully developed by the Swiss mathematicianLudwig Schläflibefore 1853. Schläfli's work received little attention during his lifetime and was published only posthumously, in 1901,but meanwhile the fourth Euclidean dimension was rediscovered by others. In 1880Charles Howard Hintonpopularized it in an essay, "What is the Fourth Dimension?",in which he explained the concept of a"four-dimensional cube"with a step-by-step generalization of the properties of lines, squares, and cubes. The simplest form of Hinton's method is to draw two ordinary 3D cubes in 2D space, one encompassing the other, separated by an" unseen "distance, and then draw lines between their equivalent vertices. This can be seen in the accompanying animation whenever it shows a smaller inner cube inside a larger outer cube. The eight lines connecting the vertices of the two cubes in this case represent asingle directionin the "unseen" fourth dimension.

Higher-dimensional spaces (greater than three) have since become one of the foundations for formally expressing modern mathematics and physics. Large parts of these topics could not exist in their current forms without using such spaces.Einstein'stheory of relativityis formulated in 4D space, although not in a Euclidean 4D space. Einstein's concept ofspacetimehas aMinkowski structurebased on anon-Euclidean geometrywith three spatial dimensions and one temporal dimension, rather than the four symmetric spatial dimensions ofSchläfli's Euclidean 4D space.

Single locations in Euclidean 4D space can be given asvectorsor4-tuples,i.e., as ordered lists of numbers such as(x,y,z,w).It is only when such locations are linked together into more complicated shapes that the full richness and geometric complexity of higher-dimensional spaces emerge. A hint of that complexity can be seen in the accompanying 2D animation of one of the simplest possibleregular 4D objects,thetesseract,which isanalogousto the 3Dcube.

History

Lagrangewrote in hisMécanique analytique(published 1788, based on work done around 1755) thatmechanicscan be viewed as operating in a four-dimensional space— three dimensions of space, and one of time.As early as 1827,Möbiusrealized that a fourthspatialdimension would allow a three-dimensional form to be rotated onto its mirror-image.The general concept ofEuclidean spacewith any number of dimensions was fully developed by the Swiss mathematicianLudwig Schläfliin the mid-19th century, at a time whenCayley,GrassmanandMöbiuswere the only other people who had ever conceived the possibility of geometry in more than three dimensions.By 1853 Schläfli had discovered all the regularpolytopesthat exist in higher dimensions, including thefour-dimensional analogsof thePlatonic solids.

An arithmetic of four spatial dimensions, calledquaternions,was defined byWilliam Rowan Hamiltonin 1843. Thisassociative algebrawas the source of the science ofvector analysisin three dimensions as recounted byMichael J. CroweinA History of Vector Analysis.Soon after,tessarinesandcoquaternionswere introduced as other four-dimensionalalgebras overR.In 1886,Victor Schlegeldescribedhis method of visualizingfour-dimensional objectswithSchlegel diagrams.

One of the first popular expositors of the fourth dimension wasCharles Howard Hinton,starting in 1880 with his essayWhat is the Fourth Dimension?,published in theDublin Universitymagazine.He coined the termstesseract,anaandkatain his bookA New Era of Thoughtand introduced a method for visualizing the fourth dimension using cubes in the bookFourth Dimension.Hinton's ideas inspired a fantasy about a "Church of the Fourth Dimension" featured byMartin Gardnerin his January 1962 "Mathematical Games column"inScientific American.

Higher dimensional non-Euclidean spaces were put on a firm footing byBernhard Riemann's 1854thesis,Über die Hypothesen welche der Geometrie zu Grunde liegen,in which he considered a "point" to be any sequence of coordinates(x₁,...,x_n).In 1908,Hermann Minkowskipresented a paperconsolidating the role of time as the fourth dimension ofspacetime,the basis forEinstein'stheories ofspecialandgeneral relativity.But the geometry of spacetime, beingnon-Euclidean,is profoundly different from that explored by Schläfli and popularised by Hinton. The study ofMinkowski spacerequired Riemann's mathematics which is quite different from that of four-dimensional Euclidean space, and so developed along quite different lines. This separation was less clear in the popular imagination, with works of fiction and philosophy blurring the distinction, so in 1973H. S. M. Coxeterfelt compelled to write:

Little, if anything, is gained by representing the fourth Euclidean dimension astime.In fact, this idea, so attractively developed byH. G. Wells inThe Time Machine,has led such authors asJohn William Dunne (An Experiment with Time)into a serious misconception of the theory of Relativity. Minkowski's geometry of space-time isnotEuclidean, and consequently has no connection with the present investigation.

— H. S. M. Coxeter,Regular Polytopes

Vectors

Mathematically, a four-dimensional space is aspacethat needs four parameters to specify apointin it. For example, a general point might have positionvectora,equal to

$\mathbf {a} ={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\\a_{4}\end{pmatrix}}.$

This can be written in terms of the fourstandard basisvectors(e₁,e₂,e₃,e₄),given by

$\mathbf {e} _{1}={\begin{pmatrix}1\\0\\0\\0\end{pmatrix}};\mathbf {e} _{2}={\begin{pmatrix}0\\1\\0\\0\end{pmatrix}};\mathbf {e} _{3}={\begin{pmatrix}0\\0\\1\\0\end{pmatrix}};\mathbf {e} _{4}={\begin{pmatrix}0\\0\\0\\1\end{pmatrix}},$

so the general vectorais

$\mathbf {a} =a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+a_{3}\mathbf {e} _{3}+a_{4}\mathbf {e} _{4}.$

Vectors add, subtract and scale as in three dimensions.

Thedot productof Euclidean three-dimensional space generalizes to four dimensions as

$\mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}+a_{4}b_{4}.$

It can be used to calculate thenormorlengthof a vector,

$\left|\mathbf {a} \right|={\sqrt {\mathbf {a} \cdot \mathbf {a} }}={\sqrt {a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2}}},$

and calculate or define theanglebetween two non-zero vectors as

$\theta =\arccos {\frac {\mathbf {a} \cdot \mathbf {b} }{\left|\mathbf {a} \right|\left|\mathbf {b} \right|}}.$

Minkowski spacetime is four-dimensional space with geometry defined by a non-degeneratepairingdifferent from the dot product:

$\mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}-a_{4}b_{4}.$

As an example, the distance squared between the points(0,0,0,0)and(1,1,1,0)is 3 in both the Euclidean and Minkowskian 4-spaces, while the distance squared between(0,0,0,0)and(1,1,1,1)is 4 in Euclidean space and 2 in Minkowski space; increasingb₄decreases the metric distance. This leads to many of the well-known apparent "paradoxes" of relativity.

Thecross productis not defined in four dimensions. Instead, theexterior productis used for some applications, and is defined as follows:

${\begin{aligned}\mathbf {a} \wedge \mathbf {b} =(a_{1}b_{2}-a_{2}b_{1})\mathbf {e} _{12}+(a_{1}b_{3}-a_{3}b_{1})\mathbf {e} _{13}+(a_{1}b_{4}-a_{4}b_{1})\mathbf {e} _{14}+(a_{2}b_{3}-a_{3}b_{2})\mathbf {e} _{23}\\+(a_{2}b_{4}-a_{4}b_{2})\mathbf {e} _{24}+(a_{3}b_{4}-a_{4}b_{3})\mathbf {e} _{34}.\end{aligned}}$

This isbivectorvalued, with bivectors in four dimensions forming asix-dimensionallinear space with basis(e₁₂,e₁₃,e₁₄,e₂₃,e₂₄,e₃₄).They can be used to generate rotations in four dimensions.

Orthogonality and vocabulary

In the familiar three-dimensional space of daily life, there are threecoordinate axes—usually labeledx,y,andz—with each axisorthogonal(i.e. perpendicular) to the other two. The six cardinal directions in this space can be calledup,down,east,west,north,andsouth.Positions along these axes can be calledaltitude,longitude,andlatitude.Lengths measured along these axes can be calledheight,width,anddepth.

Comparatively, four-dimensional space has an extra coordinate axis, orthogonal to the other three, which is usually labeledw.To describe the two additional cardinal directions,Charles Howard Hintoncoined the termsanaandkata,from the Greek words meaning "up toward" and "down from", respectively.

As mentioned above, Hermann Minkowski exploited the idea of four dimensions to discuss cosmology including the finitevelocity of light.In appending a time dimension to three-dimensional space, he specified an alternative perpendicularity,hyperbolic orthogonality.This notion provides his four-dimensional space with a modifiedsimultaneityappropriate to electromagnetic relations in his cosmos. Minkowski's world overcame problems associated with the traditionalabsolute space and timecosmology previously used in a universe of three space dimensions and one time dimension.

Geometry

See also:Rotations in 4-dimensional Euclidean space

The geometry of four-dimensional space is much more complex than that of three-dimensional space, due to the extra degree of freedom.

Just as in three dimensions there arepolyhedramade of two dimensionalpolygons,in four dimensions there are polychora made of polyhedra. In three dimensions, there are 5 regular polyhedra known as thePlatonic solids.In four dimensions, there are 6convex regular 4-polytopes,the analogs of the Platonic solids. Rela xing the conditions for regularity generates a further 58 convexuniform 4-polytopes,analogous to the 13 semi-regularArchimedean solidsin three dimensions. Rela xing the conditions for convexity generates a further 10 nonconvex regular 4-polytopes.

Regular polytopes in four dimensions
(Displayed as orthogonal projections in eachCoxeter planeof symmetry)

A4,[3,3,3]	B4,[4,3,3]		F4,[3,4,3]	H4,[5,3,3]
5-cell {3,3,3}	tesseract {4,3,3}	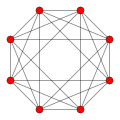16-cell {3,3,4}	24-cell {3,4,3}	600-cell {3,3,5}	120-cell {5,3,3}

In three dimensions, a circle may beextrudedto form acylinder.In four dimensions, there are several different cylinder-like objects. A sphere may be extruded to obtain a spherical cylinder (a cylinder with spherical "caps", known as aspherinder), and a cylinder may be extruded to obtain a cylindrical prism (a cubinder).TheCartesian productof two circles may be taken to obtain aduocylinder.All three can "roll" in four-dimensional space, each with its properties.

In three dimensions, curves can formknotsbut surfaces cannot (unless they are self-intersecting). In four dimensions, however, knots made using curves can be trivially untied by displacing them in the fourth direction—but 2D surfaces can form non-trivial, non-self-intersecting knots in 4D space.Because these surfaces are two-dimensional, they can form much more complex knots than strings in 3D space can. TheKlein bottleis an example of such a knotted surface.Another such surface is thereal projective plane.

Hypersphere

Stereographic projectionof aClifford torus:the set of points(cos(a), sin(a), cos(b), sin(b)),which is a subset of the3-sphere.

Main article:Hypersphere

The set of points inEuclidean 4-spacehaving the same distanceRfrom a fixed pointP₀forms ahypersurfaceknown as a3-sphere.The hyper-volume of the enclosed space is:

$\mathbf {V} ={\begin{matrix}{\frac {1}{2}}\end{matrix}}\pi ^{2}R^{4}$

This is part of theFriedmann–Lemaître–Robertson–Walker metricinGeneral relativitywhereRis substituted by functionR(t)withtmeaning the cosmological age of the universe. Growing or shrinkingRwith time means expanding or collapsing universe, depending on the mass density inside.

Four-dimensional perception in humans

Research usingvirtual realityfinds that humans, despite living in a three-dimensional world, can, without special practice, make spatial judgments about line segments embedded in four-dimensional space, based on their length (one-dimensional) and the angle (two-dimensional) between them.The researchers noted that "the participants in our study had minimal practice in these tasks, and it remains an open question whether it is possible to obtain more sustainable, definitive, and richer 4D representations with increased perceptual experience in 4D virtual environments".In another study,the ability of humans to orient themselves in 2D, 3D, and 4D mazes has been tested. Each maze consisted of four path segments of random length and connected with orthogonal random bends, but without branches or loops (i.e. actuallylabyrinths). The graphical interface was based on John McIntosh's free 4D Maze game.The participating persons had to navigate through the path and finally estimate the linear direction back to the starting point. The researchers found that some of the participants were able to mentally integrate their path after some practice in 4D (the lower-dimensional cases were for comparison and for the participants to learn the method).

However, a 2020 review underlined how these studies are composed of a small subject sample and mainly of college students. It also pointed out other issues that future research has to resolve: elimination ofartifacts(these could be caused, for example, by strategies to resolve the required task that don't use 4D representation/4D reasoning and feedback given by researchers to speed up the adaptation process) and analysis on inter-subject variability (if 4D perception is possible, its acquisition could be limited to a subset of humans, to a specificcritical period,or to people's attention or motivation). Furthermore, it is undetermined if there is a more appropriate way to project the 4-dimension (because there are no restrictions on how the 4-dimension can be projected). Researchers also hypothesized that human acquisition of 4D perception could result in the activation of brain visual areas andentorhinal cortex.If so they suggest that it could be used as a strong indicator of 4D space perception acquisition. Authors also suggested using a variety of differentneural network architectures(with differenta prioriassumptions) to understand which ones are or are not able to learn.

Dimensional analogy

A net of a tesseract

To understand the nature of four-dimensional space, a device calleddimensional analogyis commonly employed. Dimensional analogy is the study of how (n− 1) dimensions relate tondimensions, and then inferring howndimensions would relate to (n+ 1) dimensions.

The dimensional analogy was used byEdwin Abbott Abbottin the bookFlatland,which narrates a story about a square that lives in a two-dimensional world, like the surface of a piece of paper. From the perspective of this square, a three-dimensional being has seemingly god-like powers, such as ability to remove objects from a safe without breaking it open (by moving them across the third dimension), to see everything that from the two-dimensional perspective is enclosed behind walls, and to remain completely invisible by standing a few inches away in the third dimension.

By applying dimensional analogy, one can infer that a four-dimensional being would be capable of similar feats from the three-dimensional perspective.Rudy Ruckerillustrates this in his novelSpaceland,in which the protagonist encounters four-dimensional beings who demonstrate such powers.

Cross-sections

As a three-dimensional object passes through a two-dimensional plane, two-dimensional beings in this plane would only observe across-sectionof the three-dimensional object within this plane. For example, if a sphere passed through a sheet of paper, beings in the paper would see first a single point. A circle gradually grows larger, until it reaches the diameter of the sphere, and then gets smaller again, until it shrinks to a point and disappears. The 2D beings would not see a circle in the same way as three-dimensional beings do; rather, they only see aone-dimensionalprojection of the circle on their 1D "retina". Similarly, if a four-dimensional object passed through a three-dimensional (hyper) surface, one could observe a three-dimensional cross-section of the four-dimensional object. For example, ahyperspherewould appear first as a point, then as a growing sphere (until it reaches the "hyperdiameter" of the hypersphere), with the sphere then shrinking to a single point and then disappearing.This means of visualizing aspects of the fourth dimension was used in the novelFlatlandand also in several works ofCharles Howard Hinton.And, in the same way, three-dimensional beings (such as humans with a 2D retina) can see all the sides and the insides of a 2D shape simultaneously, a 4D being could see all faces and the inside of a 3D shape at once with their 3D retina.

Projections

A useful application of dimensional analogy in visualizing higher dimensions is inprojection.A projection is a way of representing ann-dimensional object inn− 1dimensions. For instance, computer screens are two-dimensional, and all the photographs of three-dimensional people, places, and things are represented in two dimensions by projecting the objects onto a flat surface. By doing this, the dimension orthogonal to the screen (depth) is removed and replaced with indirect information. Theretinaof theeyeis also a two-dimensionalarrayofreceptorsbut thebraincan perceive the nature of three-dimensional objects by inference from indirect information (such as shading,foreshortening,binocular vision,etc.).Artistsoften useperspectiveto give an illusion of three-dimensional depth to two-dimensional pictures. Theshadow,cast by a fictitious grid model of a rotating tesseract on a plane surface, as shown in the figures, is also the result of projections.

Similarly, objects in the fourth dimension can be mathematically projected to the familiar three dimensions, where they can be more conveniently examined. In this case, the 'retina' of the four-dimensional eye is a three-dimensional array of receptors. A hypothetical being with such an eye would perceive the nature of four-dimensional objects by inferring four-dimensional depth from indirect information in the three-dimensional images in its retina.

The perspective projection of three-dimensional objects into the retina of the eye introduces artifacts such as foreshortening, which the brain interprets as depth in the third dimension. In the same way, perspective projection from four dimensions produces similar foreshortening effects. By applying dimensional analogy, one may infer four-dimensional "depth" from these effects.

As an illustration of this principle, the following sequence of images compares various views of the three-dimensionalcubewith analogous projections of the four-dimensional tesseract into three-dimensional space.

Cube	Tesseract	Description
		The image on the left is a cube viewed face-on. The analogous viewpoint of the tesseract in 4 dimensions is thecell-first perspective projection,shown on the right. One may draw an analogy between the two: just as the cube projects to a square, the tesseract projects to a cube. Note that the other 5 faces of the cube are not seen here. They areobscuredby the visible face. Similarly, the other 7 cells of the tesseract are not seen here because they are obscured by the visible cell.
		The image on the left shows the same cube viewed edge-on. The analogous viewpoint of a tesseract is theface-first perspective projection,shown on the right. Just as the edge-first projection of the cube consists of twotrapezoids,the face-first projection of the tesseract consists of twofrustums. The nearest edge of the cube in this viewpoint is the one lying between the red and green faces. Likewise, the nearest face of the tesseract is the one lying between the red and green cells.
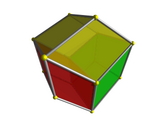
		On the left is the cube viewed corner-first. This is analogous to theedge-first perspective projectionof the tesseract, shown on the right. Just as the cube's vertex-first projection consists of 3deltoidssurrounding a vertex, the tesseract's edge-first projection consists of 3hexahedralvolumes surrounding an edge. Just as the nearest vertex of the cube is the one where the three faces meet, the nearest edge of the tesseract is the one in the center of the projection volume, where the three cells meet.
		A different analogy may be drawn between the edge-first projection of the tesseract and the edge-first projection of the cube. The cube's edge-first projection has two trapezoids surrounding an edge, while the tesseract hasthreehexahedral volumes surrounding an edge.
		On the left is the cube viewed corner-first. Thevertex-first perspective projectionof the tesseract is shown on the right. The cube's vertex-first projection has three tetragons surrounding a vertex, but the tesseract's vertex-first projection hasfourhexahedral volumes surrounding a vertex. Just as the nearest corner of the cube is the one lying at the center of the image, so the nearest vertex of the tesseract lies not on the boundary of the projected volume, but at its centerinside,where all four cells meet. Only three of the cube's six faces can be seen here, because the other three faces liebehindthese three faces, on the opposite side of the cube. Similarly, only four of the tesseract's eight cells can be seen here; the remaining four liebehindthese four in the fourth direction, on the far side of the tesseract.

Shadows

A concept closely related to projection is the casting of shadows.

If a light is shone on a three-dimensional object, a two-dimensional shadow is cast. By dimensional analogy, light shone on a two-dimensional object in a two-dimensional world would cast a one-dimensional shadow, and light on a one-dimensional object in a one-dimensional world would cast a zero-dimensional shadow, that is, a point of non-light. Going the other way, one may infer that light shining on a four-dimensional object in a four-dimensional world would cast a three-dimensional shadow.

If the wireframe of a cube is lit from above, the resulting shadow on a flat two-dimensional surface is a square within a square with the corresponding corners connected. Similarly, if the wireframe of a tesseract were lit from "above" (in the fourth dimension), its shadow would be that of a three-dimensional cube within another three-dimensional cube suspended in midair (a "flat" surface from a four-dimensional perspective). (Note that, technically, the visual representation shown here is a two-dimensional image of the three-dimensional shadow of the four-dimensional wireframe figure.)

Bounding regions

The dimensional analogy also helps in inferring basic properties of objects in higher dimensions, such as thebounding region.For example, two-dimensional objects are bounded by one-dimensional boundaries: a square is bounded by four edges. Three-dimensional objects are bounded by two-dimensional surfaces: a cube is bounded by 6 square faces.

By applying dimensional analogy, one may infer that a four-dimensional cube, known as atesseract,is bounded by three-dimensional volumes. And indeed, this is the case: mathematics shows that the tesseract is bounded by 8 cubes. Knowing this is key to understanding how to interpret a three-dimensional projection of the tesseract. The boundaries of the tesseract project tovolumesin the image, not merely two-dimensional surfaces.

Hypervolume

The4-volumeorhypervolumein 4D can be calculated in closed form for simple geometrical figures, such as the tesseract (s⁴,for side lengths) and the4-ball($\pi ^{2}r^{4}/2$for radiusr).

Reasoning by analogy from familiar lower dimensions can be an excellent intuitive guide, but care must be exercised not to accept results that are not more rigorously tested. For example, consider the formulas for the area enclosed by a circle in two dimensions ($A=\pi r^{2}$) and the volume enclosed by a sphere in three dimensions (${\textstyle V={\frac {4}{3}}\pi r^{3}}$). One might guess that the volume enclosed by the sphere in four-dimensional space is a rational multiple of$\pi r^{4}$,but the correct volume is${\frac {\pi ^{2}}{2}}r^{4}$.Thevolume of ann-ballin an arbitrary dimensionnis computable from arecurrence relationconnecting dimensionnto dimensionn- 2.

In culture

In art

This section is an excerpt fromFourth dimension in art.[edit]

An illustration from Jouffret'sTraité élémentaire de géométrie à quatre dimensions.The book, which influenced Picasso, was given to him by Princet.

New possibilities opened up by the concept of four-dimensional space (and difficulties involved in trying to visualize it) helped inspire many modern artists in the first half of the twentieth century. EarlyCubists,Surrealists,Futurists,andabstractartists took ideas fromhigher-dimensionalmathematics and used them to radically advance their work.

In literature

Main article:Fourth dimension in literature

Science fictiontexts often mention the concept of "dimension" when referring toparallel or alternate universesor other imaginedplanes of existence.This usage is derived from the idea that to travel to parallel/alternate universes/planes of existence one must travel in a direction/dimension besides the standard ones. In effect, the other universes/planes are just a small distance away from our own, but the distance is in a fourth (or higher) spatial (or non-spatial) dimension, not the standard ones.

One of the most heralded science fiction stories regarding true geometric dimensionality, and often recommended as a starting point for those just starting to investigate such matters, is the 1884 novellaFlatlandby Edwin A. Abbott. Isaac Asimov, in his foreword to the Signet Classics 1984 edition, describedFlatlandas "The best introduction one can find into the manner of perceiving dimensions."

The idea of other dimensions was incorporated into many early science fiction stories, appearing prominently, for example, inMiles J. Breuer'sThe Appendix and the Spectacles(1928) andMurray Leinster'sThe Fifth-Dimension Catapult(1931); and appeared irregularly in science fiction by the 1940s. Classic stories involving other dimensions includeRobert A. Heinlein's—And He Built a Crooked House(1941), in which a California architect designs a house based on a three-dimensional projection of a tesseract;Alan E. Nourse'sTiger by the TailandThe Universe Between(both 1951); andThe Ifth of Oofth(1957) byWalter Tevis.Another reference isMadeleine L'Engle's novelA Wrinkle In Time(1962), which uses the fifth dimension as a way of "tesseracting the universe" or "folding" space to move across it quickly. The fourth and fifth dimensions are also key components of the bookThe Boy Who Reversed HimselfbyWilliam Sleator.

In philosophy

Immanuel Kantwrote in 1783: "That everywhere space (which is not itself the boundary of another space) has three dimensions and that space, in general, cannot have more dimensions is based on the proposition that not more than three lines can intersect at right angles in one point. This proposition cannot at all be shown from concepts, but rests immediately on intuition and indeed on pure intuitiona prioribecause it is apodictically (demonstrably) certain. "

"Space has Four Dimensions" is a short story published in 1846 by German philosopher andexperimental psychologistGustav Fechnerunder thepseudonym"Dr. Mises". The protagonist in the tale is a shadow who is aware of and able to communicate with other shadows, but who is trapped on a two-dimensional surface. According to Fechner, this "shadow-man" would conceive of the third dimension as being one of time.The story bears a strong similarity to the "Allegory of the Cave"presented inPlato'sThe Republic(c.380 BC).

Simon Newcomb wrote an article for theBulletin of the American Mathematical Societyin 1898 entitled "The Philosophy of Hyperspace".Linda Dalrymple Hendersoncoined the term "hyperspace philosophy", used to describe writing that uses higher dimensions to exploremetaphysicalthemes, in her 1983 thesis about the fourth dimension in early-twentieth-century art.Examples of "hyperspace philosophers" includeCharles Howard Hinton,the first writer, in 1888, to use the word "tesseract";and the RussianesotericistP. D. Ouspensky.

See also

• 4-polytope
• 4-manifold
• ExoticR⁴
• Four-dimensionalism
• List of four-dimensional games
• Time in physics
• Spacetime

References

• Schläfli, Ludwig (1901) [1852], Graf, J. H. (ed.),Theorie der vielfachen Kontinuität,Republished by Cornell University Library historical math monographs 2010 (in German), Zürich, Basel: Georg & Co.,ISBN978-1-4297-0481-6
• Coxeter, H.S.M.(1973) [1948].Regular Polytopes(3rd ed.). New York: Dover.

Further reading

• Archibald, R. C(1914)."Time as a Fourth Dimension"(PDF).Bulletin of the American Mathematical Society:409–412.
• Andrew Forsyth(1930)Geometry of Four Dimensions,link fromInternet Archive.
• Gamow, George(1988).One Two Three... Infinity: Facts and Speculations of Science(3rd ed.). Courier Dover Publications. p. 68.ISBN978-0-486-25664-1.Extract of page 68
• E. H. Neville(1921)The Fourth Dimension,Cambridge University Press,link fromUniversity of MichiganHistorical Math Collection.

External links

• "Dimensions" videos, showing several different ways to visualize four-dimensional objects
• Science Newsarticle summarizing the "Dimensions" videos, with clipsArchived2012-09-29 at theWayback Machine
• Flatland: a Romance of Many Dimensions(second edition)
• Frame-by-frame animations of 4D - 3D analogies