Hash table
| Hash table | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | Unorderedassociative array | |||||||||||||||||||||||
| Invented | 1953 | |||||||||||||||||||||||
| ||||||||||||||||||||||||
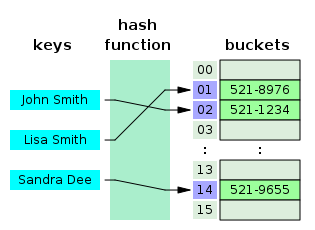
Incomputing,ahash tableis adata structurethat implements anassociative array,also called adictionaryor simplymap;an associative array is anabstract data typethat mapskeystovalues.[2]A hash table uses ahash functionto compute anindex,also called ahash code,into an array ofbucketsorslots,from which the desired value can be found. During lookup, the key is hashed and the resulting hash indicates where the corresponding value is stored. A map implemented by a hash table is called ahash map.
Most hash table designs employ animperfect hash function.Hash collisions,where the hash function generates the same index for more than one key, therefore typically must be accommodated in some way.
In a well-dimensioned hash table, the average time complexity for each lookup is independent of the number of elements stored in the table. Many hash table designs also allow arbitrary insertions and deletions ofkey–value pairs,atamortizedconstant average cost per operation.[3][4][5]
Hashing is an example of aspace-time tradeoff.Ifmemoryis infinite, the entire key can be used directly as an index to locate its value with a single memory access. On the other hand, if infinite time is available, values can be stored without regard for their keys, and abinary searchorlinear searchcan be used to retrieve the element.[6]: 458
In many situations, hash tables turn out to be on average more efficient thansearch treesor any othertablelookup structure. For this reason, they are widely used in many kinds of computersoftware,particularly forassociative arrays,database inde xing,caches,andsets.
History
[edit]The idea of hashing arose independently in different places. In January 1953,Hans Peter Luhnwrote an internalIBMmemorandum that used hashing with chaining. The first example ofopen addressingwas proposed by A. D. Linh, building on Luhn's memorandum.[4]: 547 Around the same time,Gene Amdahl,Elaine M. McGraw,Nathaniel Rochester,andArthur SamuelofIBM Researchimplemented hashing for theIBM 701assembler.[7]: 124 Open addressing with linear probing is credited to Amdahl, althoughAndrey Ershovindependently had the same idea.[7]: 124–125 The term "open addressing" was coined byW. Wesley Petersonin his article which discusses the problem of search in large files.[8]: 15
The firstpublishedwork on hashing with chaining is credited toArnold Dumey,who discussed the idea of using remainder modulo a prime as a hash function.[8]: 15 The word "hashing" was first published in an article by Robert Morris.[7]: 126 Atheoretical analysisof linear probing was submitted originally by Konheim and Weiss.[8]: 15
Overview
[edit]Anassociative arraystores asetof (key, value) pairs and allows insertion, deletion, and lookup (search), with the constraint ofunique keys.In the hash table implementation of associative arrays, an arrayof lengthis partially filled withelements, where.A valuegets stored at an index location,whereis a hash function, and.[8]: 2 Under reasonable assumptions, hash tables have bettertime complexitybounds on search, delete, and insert operations in comparison toself-balancing binary search trees.[8]: 1
Hash tables are also commonly used to implement sets, by omitting the stored value for each key and merely tracking whether the key is present.[8]: 1
Load factor
[edit]Aload factoris a critical statistic of a hash table, and is defined as follows:[1] where
- is the number of entries occupied in the hash table.
- is the number of buckets.
The performance of the hash table deteriorates in relation to the load factor.[8]: 2
The software typically ensures that the load factorremains below a certain constant,.This helps maintain good performance. Therefore, a common approach is to resize or "rehash" the hash table whenever the load factorreaches.Similarly the table may also be resized if the load factor drops below.[9]
Load factor for separate chaining
[edit]With separate chaining hash tables, each slot of the bucket array stores a pointer to a list or array of data.[10]
Separate chaining hash tables suffer gradually declining performance as the load factor grows, and no fixed point beyond which resizing is absolutely needed.[9]
With separate chaining, the value ofthat gives best performance is typically between 1 and 3.[9]
Load factor for open addressing
[edit]With open addressing, each slot of the bucket array holds exactly one item. Therefore an open-addressed hash table cannot have a load factor greater than 1.[10]
The performance of open addressing becomes very bad when the load factor approaches 1.[9]
Therefore a hash table that uses open addressingmustbe resized orrehashedif the load factorapproaches 1.[9]
With open addressing, acceptable figures of max load factorshould range around 0.6 to 0.75.[11][12]: 110
Hash function
[edit]Ahash functionmaps the universeof keys to indices or slots within the table, that is,for.The conventional implementations of hash functions are based on theinteger universe assumptionthat all elements of the table stem from the universe,where thebit lengthofis confined within theword sizeof acomputer architecture.[8]: 2
A hash functionis said to beperfectfor a given setif it isinjectiveon,that is, if each elementmaps to a different value in.[13][14]A perfect hash function can be created if all the keys are known ahead of time.[13]
Integer universe assumption
[edit]The schemes of hashing used ininteger universe assumptioninclude hashing by division, hashing by multiplication,universal hashing,dynamic perfect hashing,andstatic perfect hashing.[8]: 2 However, hashing by division is the commonly used scheme.[15]: 264 [12]: 110
Hashing by division
[edit]The scheme in hashing by division is as follows:[8]: 2 whereis the hash value ofandis the size of the table.
Hashing by multiplication
[edit]The scheme in hashing by multiplication is as follows:[8]: 2–3 Whereis a non-integerreal-valued constantandis the size of the table. An advantage of the hashing by multiplication is that theis not critical.[8]: 2–3 Although any valueproduces a hash function,Donald Knuthsuggests using thegolden ratio.[8]: 3
Choosing a hash function
[edit]Uniform distributionof the hash values is a fundamental requirement of a hash function. A non-uniform distribution increases the number of collisions and the cost of resolving them. Uniformity is sometimes difficult to ensure by design, but may be evaluated empirically using statistical tests, e.g., aPearson's chi-squared testfor discrete uniform distributions.[16][17]
The distribution needs to be uniform only for table sizes that occur in the application. In particular, if one uses dynamic resizing with exact doubling and halving of the table size, then the hash function needs to be uniform only when the size is apower of two.Here the index can be computed as some range of bits of the hash function. On the other hand, some hashing algorithms prefer to have the size be aprime number.[18]
Foropen addressingschemes, the hash function should also avoidclustering,the mapping of two or more keys to consecutive slots. Such clustering may cause the lookup cost to skyrocket, even if the load factor is low and collisions are infrequent. The popular multiplicative hash is claimed to have particularly poor clustering behavior.[18][4]
K-independent hashingoffers a way to prove a certain hash function does not have bad keysets for a given type of hashtable. A number of K-independence results are known for collision resolution schemes such as linear probing and cuckoo hashing. Since K-independence can prove a hash function works, one can then focus on finding the fastest possible such hash function.[19]
Collision resolution
[edit]A search algorithm that uses hashing consists of two parts. The first part is computing ahash functionwhich transforms the search key into anarray index.The ideal case is such that no two search keys hashes to the same array index. However, this is not always the case and is impossible to guarantee for unseen given data.[20]: 515 Hence the second part of the algorithm is collision resolution. The two common methods for collision resolution are separate chaining and open addressing.[6]: 458
Separate chaining
[edit]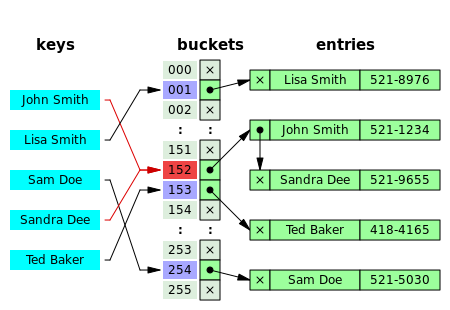

In separate chaining, the process involves building alinked listwithkey–value pairfor each search array index. The collided items are chained together through a single linked list, which can be traversed to access the item with a unique search key.[6]: 464 Collision resolution through chaining with linked list is a common method of implementation of hash tables. Letandbe the hash table and the node respectively, the operation involves as follows:[15]: 258
Chained-Hash-Insert(T,k) insertxat the head of linked listT[h(k)] Chained-Hash-Search(T,k) search for an element with keykin linked listT[h(k)] Chained-Hash-Delete(T,k) deletexfrom the linked listT[h(k)]
If the element is comparable eithernumericallyorlexically,and inserted into the list by maintaining thetotal order,it results in faster termination of the unsuccessful searches.[20]: 520–521
Other data structures for separate chaining
[edit]If the keys areordered,it could be efficient to use "self-organizing"concepts such as using aself-balancing binary search tree,through which thetheoretical worst casecould be brought down to,although it introduces additional complexities.[20]: 521
Indynamic perfect hashing,two-level hash tables are used to reduce the look-up complexity to be a guaranteedin the worst case. In this technique, the buckets ofentries are organized asperfect hash tableswithslots providing constant worst-case lookup time, and low amortized time for insertion.[21]A study shows array-based separate chaining to be 97% more performant when compared to the standard linked list method under heavy load.[22]: 99
Techniques such as usingfusion treefor each buckets also result in constant time for all operations with high probability.[23]
Caching and locality of reference
[edit]The linked list of separate chaining implementation may not becache-consciousdue tospatial locality—locality of reference—when the nodes of the linked list are scattered across memory, thus the list traversal during insert and search may entailCPU cacheinefficiencies.[22]: 91
Incache-conscious variantsof collision resolution through separate chaining, adynamic arrayfound to be morecache-friendlyis used in the place where a linked list or self-balancing binary search trees is usually deployed, since thecontiguous allocationpattern of the array could be exploited byhardware-cache prefetchers—such astranslation lookaside buffer—resulting in reduced access time and memory consumption.[24][25][26]
Open addressing
[edit]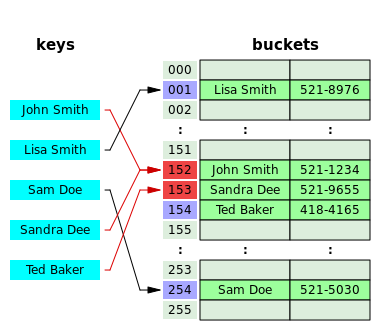

Open addressingis another collision resolution technique in which every entry record is stored in the bucket array itself, and the hash resolution is performed throughprobing.When a new entry has to be inserted, the buckets are examined, starting with the hashed-to slot and proceeding in someprobe sequence,until an unoccupied slot is found. When searching for an entry, the buckets are scanned in the same sequence, until either the target record is found, or an unused array slot is found, which indicates an unsuccessful search.[27]
Well-known probe sequences include:
- Linear probing,in which the interval between probes is fixed (usually 1).[28]
- Quadratic probing,in which the interval between probes is increased by adding the successive outputs of a quadratic polynomial to the value given by the original hash computation.[29]: 272
- Double hashing,in which the interval between probes is computed by a secondary hash function.[29]: 272–273
The performance of open addressing may be slower compared to separate chaining since the probe sequence increases when the load factorapproaches 1.[9][22]: 93 The probing results in aninfinite loopif the load factor reaches 1, in the case of a completely filled table.[6]: 471 Theaverage costof linear probing depends on the hash function's ability todistributethe elementsuniformlythroughout the table to avoidclustering,since formation of clusters would result in increased search time.[6]: 472
Caching and locality of reference
[edit]Since the slots are located in successive locations, linear probing could lead to better utilization ofCPU cachedue tolocality of referencesresulting in reducedmemory latency.[28]
Other collision resolution techniques based on open addressing
[edit]Coalesced hashing
[edit]Coalesced hashingis a hybrid of both separate chaining and open addressing in which the buckets or nodes link within the table.[30]: 6–8 The algorithm is ideally suited forfixed memory allocation.[30]: 4 The collision in coalesced hashing is resolved by identifying the largest-indexed empty slot on the hash table, then the colliding value is inserted into that slot. The bucket is also linked to the inserted node's slot which contains its colliding hash address.[30]: 8
Cuckoo hashing
[edit]Cuckoo hashingis a form of open addressing collision resolution technique which guaranteesworst-case lookup complexity and constant amortized time for insertions. The collision is resolved through maintaining two hash tables, each having its own hashing function, and collided slot gets replaced with the given item, and the preoccupied element of the slot gets displaced into the other hash table. The process continues until every key has its own spot in the empty buckets of the tables; if the procedure enters intoinfinite loop—which is identified through maintaining a threshold loop counter—both hash tables get rehashed with newer hash functions and the procedure continues.[31]: 124–125
Hopscotch hashing
[edit]Hopscotch hashingis an open addressing based algorithm which combines the elements ofcuckoo hashing,linear probingand chaining through the notion of aneighbourhoodof buckets—the subsequent buckets around any given occupied bucket, also called a "virtual" bucket.[32]: 351–352 The algorithm is designed to deliver better performance when the load factor of the hash table grows beyond 90%; it also provides high throughput inconcurrent settings,thus well suited for implementing resizableconcurrent hash table.[32]: 350 The neighbourhood characteristic of hopscotch hashing guarantees a property that, the cost of finding the desired item from any given buckets within the neighbourhood is very close to the cost of finding it in the bucket itself; the algorithm attempts to be an item into its neighbourhood—with a possible cost involved in displacing other items.[32]: 352
Each bucket within the hash table includes an additional "hop-information" —anH-bitbit arrayfor indicating therelative distanceof the item which was originally hashed into the current virtual bucket withinH-1 entries.[32]: 352 Letandbe the key to be inserted and bucket to which the key is hashed into respectively; several cases are involved in the insertion procedure such that the neighbourhood property of the algorithm is vowed:[32]: 352–353 ifis empty, the element is inserted, and the leftmost bit of bitmap issetto 1; if not empty, linear probing is used for finding an empty slot in the table, the bitmap of the bucket gets updated followed by the insertion; if the empty slot is not within the range of theneighbourhood,i.e.H-1, subsequent swap and hop-info bit array manipulation of each bucket is performed in accordance with its neighbourhoodinvariant properties.[32]: 353
Robin Hood hashing
[edit]Robin Hood hashing is an open addressing based collision resolution algorithm; the collisions are resolved through favouring the displacement of the element that is farthest—or longestprobe sequence length(PSL)—from its "home location" i.e. the bucket to which the item was hashed into.[33]: 12 Although Robin Hood hashing does not change thetheoretical search cost,it significantly affects thevarianceof thedistributionof the items on the buckets,[34]: 2 i.e. dealing withclusterformation in the hash table.[35]Each node within the hash table that uses Robin Hood hashing should be augmented to store an extra PSL value.[36]Letbe the key to be inserted,be the (incremental) PSL length of,be the hash table andbe the index, the insertion procedure is as follows:[33]: 12–13 [37]: 5
- If:the iteration goes into the next bucket without attempting an external probe.
- If:insert the iteminto the bucket;swapwith—let it be;continue the probe from thest bucket to insert;repeat the procedure until every element is inserted.
Dynamic resizing
[edit]Repeated insertions cause the number of entries in a hash table to grow, which consequently increases the load factor; to maintain the amortizedperformance of the lookup and insertion operations, a hash table is dynamically resized and the items of the tables arerehashedinto the buckets of the new hash table,[9]since the items cannot be copied over as varying table sizes results in different hash value due tomodulo operation.[38]If a hash table becomes "too empty" after deleting some elements, resizing may be performed to avoid excessivememory usage.[39]
Resizing by moving all entries
[edit]Generally, a new hash table with a size double that of the original hash table getsallocatedprivately and every item in the original hash table gets moved to the newly allocated one by computing the hash values of the items followed by the insertion operation. Rehashing is simple, but computationally expensive.[40]: 478–479
Alternatives to all-at-once rehashing
[edit]Some hash table implementations, notably inreal-time systems,cannot pay the price of enlarging the hash table all at once, because it may interrupt time-critical operations. If one cannot avoid dynamic resizing, a solution is to perform the resizing gradually to avoid storage blip—typically at 50% of new table's size—during rehashing and to avoidmemory fragmentationthat triggersheap compactiondue to deallocation of largememory blockscaused by the old hash table.[41]: 2–3 In such case, the rehashing operation is done incrementally through extending prior memory block allocated for the old hash table such that the buckets of the hash table remain unaltered. A common approach for amortized rehashing involves maintaining two hash functionsand.The process of rehashing a bucket's items in accordance with the new hash function is termed ascleaning,which is implemented throughcommand patternby encapsulating the operations such as,andthrough awrappersuch that each element in the bucket gets rehashed and its procedure involve as follows:[41]: 3
- Cleanbucket.
- Cleanbucket.
- Thecommandgets executed.
Linear hashing
[edit]Linear hashingis an implementation of the hash table which enables dynamic growths or shrinks of the table one bucket at a time.[42]
Performance
[edit]The performance of a hash table is dependent on the hash function's ability in generatingquasi-random numbers() for entries in the hash table where,anddenotes the key, number of buckets and the hash function such that.If the hash function generates the samefor distinct keys (), this results incollision,which is dealt with in a variety of ways. The constant time complexity () of the operation in a hash table is presupposed on the condition that the hash function doesn't generate colliding indices; thus, the performance of the hash table isdirectly proportionalto the chosen hash function's ability todispersethe indices.[43]: 1 However, construction of such a hash function ispractically infeasible,that being so, implementations depend oncase-specificcollision resolution techniquesin achieving higher performance.[43]: 2
Applications
[edit]Associative arrays
[edit]Hash tables are commonly used to implement many types of in-memory tables. They are used to implementassociative arrays.[29]
Database inde xing
[edit]Hash tables may also be used asdisk-based data structures anddatabase indices(such as indbm) althoughB-treesare more popular in these applications.[44]
Caches
[edit]Hash tables can be used to implementcaches,auxiliary data tables that are used to speed up the access to data that is primarily stored in slower media. In this application, hash collisions can be handled by discarding one of the two colliding entries—usually erasing the old item that is currently stored in the table and overwriting it with the new item, so every item in the table has a unique hash value.[45][46]
Sets
[edit]Hash tables can be used in the implementation ofset data structure,which can store unique values without any particular order; set is typically used in testing the membership of a value in the collection, rather than element retrieval.[47]
Transposition table
[edit]Atransposition tableto a complex Hash Table which stores information about each section that has been searched.[48]
Implementations
[edit]Many programming languages provide hash table functionality, either as built-in associative arrays or asstandard librarymodules.
InJavaScript,an "object" is a mutable collection of key-value pairs (called "properties" ), where each key is either a string or a guaranteed-unique "symbol"; any other value, when used as a key, is firstcoercedto a string. Aside from the seven "primitive" data types, every value in JavaScript is an object.[49]ECMAScript 2015 also added theMapdata structure, which accepts arbitrary values as keys.[50]
C++11includesunordered_mapin its standard library for storing keys and values ofarbitrary types.[51]
Go's built-inmapimplements a hash table in the form of atype.[52]
Javaprogramming language includes theHashSet,HashMap,LinkedHashSet,andLinkedHashMapgenericcollections.[53]
Python's built-indictimplements a hash table in the form of atype.[54]
Ruby's built-inHashuses the open addressing model from Ruby 2.4 onwards.[55]
Rustprogramming language includesHashMap,HashSetas part of the Rust Standard Library.[56]
The.NETstandard library includesHashSetandDictionary,[57][58]so it can be used from languages such asC#andVB.NET.[59]
See also
[edit]References
[edit]- ^ab Cormen, Thomas H.;Leiserson, Charles E.;Rivest, Ronald L.;Stein, Clifford(2009).Introduction to Algorithms(3rd ed.). Massachusetts Institute of Technology. pp. 253–280.ISBN978-0-262-03384-8.
- ^Mehlhorn, Kurt;Sanders, Peter(2008)."Hash Tables and Associative Arrays"(PDF).Algorithms and Data Structures.Springer. pp. 81–98.doi:10.1007/978-3-540-77978-0_4.ISBN978-3-540-77977-3.
- ^Leiserson, Charles E.(Fall 2005)."Lecture 13: Amortized Algorithms, Table Doubling, Potential Method".course MIT 6.046J/18.410J Introduction to Algorithms.Archivedfrom the original on August 7, 2009.
- ^abcKnuth, Donald(1998).The Art of Computer Programming.Vol. 3:Sorting and Searching(2nd ed.). Addison-Wesley. pp. 513–558.ISBN978-0-201-89685-5.
- ^Cormen, Thomas H.;Leiserson, Charles E.;Rivest, Ronald L.;Stein, Clifford(2001). "Chapter 11: Hash Tables".Introduction to Algorithms(2nd ed.). MIT Press and McGraw-Hill. pp.221–252.ISBN978-0-262-53196-2.
- ^abcdeSedgewick, Robert;Wayne, Kevin (2011).Algorithms.Vol. 1 (4 ed.). Addison-Wesley Professional – viaPrinceton University,Department of Computer Science.
- ^abcKonheim, Alan G. (2010).Hashing in Computer Science.doi:10.1002/9780470630617.ISBN978-0-470-34473-6.
- ^abcdefghijklmMehta, Dinesh P.; Mehta, Dinesh P.; Sahni, Sartaj, eds. (2004).Handbook of Data Structures and Applications.doi:10.1201/9781420035179.ISBN978-0-429-14701-2.
- ^abcdefgMayers, Andrew (2008)."CS 312: Hash tables and amortized analysis".Cornell University,Department of Computer Science.Archivedfrom the original on April 26, 2021.RetrievedOctober 26,2021– via cs.cornell.edu.
- ^ab James S. Plank and Brad Vander Zanden. "CS140 Lecture notes -- Hashing".
- ^Maurer, W. D.; Lewis, T. G. (March 1975). "Hash Table Methods".ACM Computing Surveys.7(1): 5–19.doi:10.1145/356643.356645.S2CID17874775.
- ^abOwolabi, Olumide (February 2003). "Empirical studies of some hashing functions".Information and Software Technology.45(2): 109–112.doi:10.1016/S0950-5849(02)00174-X.
- ^abLu, Yi; Prabhakar, Balaji; Bonomi, Flavio (2006).Perfect Hashing for Network Applications.2006 IEEE International Symposium on Information Theory. pp. 2774–2778.doi:10.1109/ISIT.2006.261567.ISBN1-4244-0505-X.S2CID1494710.
- ^Belazzougui, Djamal; Botelho, Fabiano C.; Dietzfelbinger, Martin (2009)."Hash, displace, and compress"(PDF).Algorithms—ESA 2009: 17th Annual European Symposium, Copenhagen, Denmark, September 7–9, 2009, Proceedings.Lecture Notes in Computer Science.Vol. 5757. Berlin: Springer. pp. 682–693.CiteSeerX10.1.1.568.130.doi:10.1007/978-3-642-04128-0_61.MR2557794.
- ^abCormen, Thomas H.;Leiserson, Charles E.;Rivest, Ronald L.;Stein, Clifford(2001). "Chapter 11: Hash Tables".Introduction to Algorithms(2nd ed.).Massachusetts Institute of Technology.ISBN978-0-262-53196-2.
- ^Pearson, Karl(1900)."On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling".Philosophical Magazine.Series 5.50(302): 157–175.doi:10.1080/14786440009463897.
- ^Plackett, Robin(1983). "Karl Pearson and the Chi-Squared Test".International Statistical Review.51(1): 59–72.doi:10.2307/1402731.JSTOR1402731.
- ^abWang, Thomas (March 1997)."Prime Double Hash Table".Archived fromthe originalon September 3, 1999.RetrievedMay 10,2015.
- ^Wegman, Mark N.; Carter, J.Lawrence (June 1981)."New hash functions and their use in authentication and set equality".Journal of Computer and System Sciences.22(3): 265–279.doi:10.1016/0022-0000(81)90033-7.
- ^abcDonald E. Knuth(April 24, 1998).The Art of Computer Programming: Volume 3: Sorting and Searching.Addison-Wesley Professional.ISBN978-0-201-89685-5.
- ^Demaine, Erik; Lind, Jeff (Spring 2003)."Lecture 2"(PDF).6.897: Advanced Data Structures. MIT Computer Science and Artificial Intelligence Laboratory.Archived(PDF)from the original on June 15, 2010.RetrievedJune 30,2008.
- ^abcCulpepper, J. Shane; Moffat, Alistair (2005). "Enhanced Byte Codes with Restricted Prefix Properties".String Processing and Information Retrieval.Lecture Notes in Computer Science. Vol. 3772. pp. 1–12.doi:10.1007/11575832_1.ISBN978-3-540-29740-6.
- ^Willard, Dan E.(2000). "Examining computational geometry, van Emde Boas trees, and hashing from the perspective of the fusion tree".SIAM Journal on Computing.29(3): 1030–1049.doi:10.1137/S0097539797322425.MR1740562..
- ^Askitis, Nikolas; Sinha, Ranjan (October 2010). "Engineering scalable, cache and space efficient tries for strings".The VLDB Journal.19(5): 633–660.doi:10.1007/s00778-010-0183-9.
- ^Askitis, Nikolas; Zobel, Justin (October 2005). "Cache-conscious Collision Resolution in String Hash Tables".Proceedings of the 12th International Conference, String Processing and Information Retrieval (SPIRE 2005).Vol. 3772/2005. pp. 91–102.doi:10.1007/11575832_11.ISBN978-3-540-29740-6.
- ^Askitis, Nikolas (2009)."Fast and Compact Hash Tables for Integer Keys"(PDF).Proceedings of the 32nd Australasian Computer Science Conference (ACSC 2009).Vol. 91. pp. 113–122.ISBN978-1-920682-72-9.Archived fromthe original(PDF)on February 16, 2011.RetrievedJune 13,2010.
- ^Tenenbaum, Aaron M.; Langsam, Yedidyah; Augenstein, Moshe J. (1990).Data Structures Using C.Prentice Hall. pp. 456–461, p. 472.ISBN978-0-13-199746-2.
- ^abPagh, Rasmus;Rodler, Flemming Friche (2001). "Cuckoo Hashing".Algorithms — ESA 2001.Lecture Notes in Computer Science. Vol. 2161. pp. 121–133.CiteSeerX10.1.1.25.4189.doi:10.1007/3-540-44676-1_10.ISBN978-3-540-42493-2.
- ^abcCormen, Thomas H.;Leiserson, Charles E.;Rivest, Ronald L.;Stein, Clifford(2001), "11 Hash Tables",Introduction to Algorithms(2nd ed.),MIT PressandMcGraw-Hill,pp. 221–252,ISBN0-262-03293-7.
- ^abcVitter, Jeffery S.; Chen, Wen-Chin (1987).The design and analysis of coalesced hashing.New York, United States:Oxford University Press.ISBN978-0-19-504182-8– viaArchive.org.
- ^Pagh, Rasmus;Rodler, Flemming Friche (2001). "Cuckoo Hashing".Algorithms — ESA 2001.Lecture Notes in Computer Science. Vol. 2161. pp. 121–133.CiteSeerX10.1.1.25.4189.doi:10.1007/3-540-44676-1_10.ISBN978-3-540-42493-2.
- ^abcdefHerlihy, Maurice; Shavit, Nir; Tzafrir, Moran (2008). "Hopscotch Hashing".Distributed Computing.Lecture Notes in Computer Science. Vol. 5218. pp. 350–364.doi:10.1007/978-3-540-87779-0_24.ISBN978-3-540-87778-3.
- ^abCelis, Pedro (1986).Robin Hood Hashing(PDF).Ontario, Canada:University of Waterloo,Dept. of Computer Science.ISBN978-0-315-29700-5.OCLC14083698.Archived(PDF)from the original on November 1, 2021.RetrievedNovember 2,2021.
- ^Poblete, P. V.; Viola, A. (July 2019). "Analysis of Robin Hood and Other Hashing Algorithms Under the Random Probing Model, With and Without Deletions".Combinatorics, Probability and Computing.28(4): 600–617.doi:10.1017/S0963548318000408.S2CID125374363.
- ^Clarkson, Michael (2014)."Lecture 13: Hash tables".Cornell University,Department of Computer Science.Archivedfrom the original on October 7, 2021.RetrievedNovember 1,2021– via cs.cornell.edu.
- ^Gries, David (2017)."JavaHyperText and Data Structure: Robin Hood Hashing"(PDF).Cornell University,Department of Computer Science.Archived(PDF)from the original on April 26, 2021.RetrievedNovember 2,2021– via cs.cornell.edu.
- ^Celis, Pedro (March 28, 1988).External Robin Hood Hashing(PDF)(Technical report). Bloomington, Indiana:Indiana University,Department of Computer Science. 246.Archived(PDF)from the original on November 3, 2021.RetrievedNovember 2,2021.
- ^Goddard, Wayne (2021)."Chapter C5: Hash Tables"(PDF).Clemson University.pp. 15–16.RetrievedDecember 4,2023.
- ^Devadas, Srini; Demaine, Erik (February 25, 2011)."Intro to Algorithms: Resizing Hash Tables"(PDF).Massachusetts Institute of Technology,Department of Computer Science.Archived(PDF)from the original on May 7, 2021.RetrievedNovember 9,2021– viaMIT OpenCourseWare.
- ^Thareja, Reema (2014). "Hashing and Collision".Data Structures Using C.Oxford University Press. pp. 464–488.ISBN978-0-19-809930-7.
- ^abFriedman, Scott; Krishnan, Anand; Leidefrost, Nicholas (March 18, 2003)."Hash Tables for Embedded and Real-time systems"(PDF).All Computer Science and Engineering Research.Washington University in St. Louis.doi:10.7936/K7WD3XXV.Archived(PDF)from the original on June 9, 2021.RetrievedNovember 9,2021– viaNorthwestern University,Department of Computer Science.
- ^Litwin, Witold (1980)."Linear hashing: A new tool for file and table addressing"(PDF).Proc. 6th Conference on Very Large Databases.Carnegie Mellon University.pp. 212–223.Archived(PDF)from the original on May 6, 2021.RetrievedNovember 10,2021– via cs.cmu.edu.
- ^abDijk, Tom Van (2010)."Analysing and Improving Hash Table Performance"(PDF).Netherlands:University of Twente.Archived(PDF)from the original on November 6, 2021.RetrievedDecember 31,2021.
- ^Lech Banachowski."Indexes and external sorting".pl:Polsko-Japońska Akademia Technik Komputerowych.Archived fromthe originalon March 26, 2022.RetrievedMarch 26,2022.
- ^Zhong, Liang; Zheng, Xueqian; Liu, Yong; Wang, Mengting; Cao, Yang (February 2020). "Cache hit ratio maximization in device-to-device communications overlaying cellular networks".China Communications.17(2): 232–238.doi:10.23919/jcc.2020.02.018.S2CID212649328.
- ^Bottommley, James (January 1, 2004)."Understanding Caching".Linux Journal.Archivedfrom the original on December 4, 2020.RetrievedApril 16,2022.
- ^Jill Seaman (2014)."Set & Hash Tables"(PDF).Texas State University.Archived from the original on April 1, 2022.RetrievedMarch 26,2022.
{{cite web}}:CS1 maint: bot: original URL status unknown (link) - ^"Transposition Table - Chessprogramming wiki".chessprogramming.org.Archivedfrom the original on February 14, 2021.RetrievedMay 1,2020.
- ^"JavaScript data types and data structures - JavaScript | MDN".developer.mozilla.org.RetrievedJuly 24,2022.
- ^"Map - JavaScript | MDN".developer.mozilla.org.June 20, 2023.RetrievedJuly 15,2023.
- ^"Programming language C++ - Technical Specification"(PDF).International Organization for Standardization.pp. 812–813. Archived fromthe original(PDF)on January 21, 2022.RetrievedFebruary 8,2022.
- ^"The Go Programming Language Specification".go.dev.RetrievedJanuary 1,2023.
- ^"Lesson: Implementations (The Java™ Tutorials > Collections)".docs.oracle.Archivedfrom the original on January 18, 2017.RetrievedApril 27,2018.
- ^Zhang, Juan; Jia, Yunwei (2020)."Redis rehash optimization based on machine learning".Journal of Physics: Conference Series.1453(1): 3.Bibcode:2020JPhCS1453a2048Z.doi:10.1088/1742-6596/1453/1/012048.S2CID215943738.
- ^Jonan Scheffler (December 25, 2016)."Ruby 2.4 Released: Faster Hashes, Unified Integers and Better Rounding".heroku.Archivedfrom the original on July 3, 2019.RetrievedJuly 3,2019.
- ^"doc.rust-lang.org".Archivedfrom the original on December 8, 2022.RetrievedDecember 14,2022.
- ^"HashSet Class (System.Collections.Generic)".learn.microsoft.RetrievedJuly 1,2023.
- ^dotnet-bot."Dictionary Class (System.Collections.Generic)".learn.microsoft.RetrievedJanuary 16,2024.
- ^"VB.NET HashSet Example".Dot Net Perls.
Further reading
[edit]- Tamassia, Roberto; Goodrich, Michael T. (2006). "Chapter Nine: Maps and Dictionaries".Data structures and algorithms in Java: [updated for Java 5.0](4th ed.). Hoboken, NJ: Wiley. pp.369–418.ISBN978-0-471-73884-8.
- McKenzie, B. J.; Harries, R.; Bell, T. (February 1990). "Selecting a hashing algorithm".Software: Practice and Experience.20(2): 209–224.doi:10.1002/spe.4380200207.hdl:10092/9691.S2CID12854386.
External links
[edit]- NISTentry onhash tables
- Open Data Structures – Chapter 5 – Hash Tables,Pat Morin
- MIT's Introduction to Algorithms: Hashing 1MIT OCW lecture Video
- MIT's Introduction to Algorithms: Hashing 2MIT OCW lecture Video






![{\displaystyle A[h(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac75d530b12267b829df7cff8b2ff01a24e61ab0)


























![{\displaystyle x.psl\ \leq \ T[j].psl}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0813eb6a21c2c8a817aa86085d3cf9417f01e8fb)
![{\displaystyle x.psl\ >\ T[j].psl}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d06f4753fda641edd5afb066239100a667124f39)
![{\displaystyle T[j]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb1f9ca1ed801caf88d5004aa3685644667099b6)








![{\displaystyle \mathrm {Table} [h_{\text{old}}(\mathrm {key} )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afcb195bb40a51be98c16b6d9b930061f3c11682)
![{\displaystyle \mathrm {Table} [h_{\text{new}}(\mathrm {key} )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8097baf3c9220a1be057b3c86395debce381845)



