Injective object

Inmathematics,especially in the field ofcategory theory,the concept ofinjective objectis a generalization of the concept ofinjective module.This concept is important incohomology,inhomotopy theoryand in the theory ofmodel categories.The dual notion is that of aprojective object.

Definition

An object`Q`is injective if, given a monomorphism`f`:`X`→`Y`,any`g`:`X`→`Q`can be extended to`Y`.

Anobject $Q$ in acategory $\mathbf {C}$ is said to beinjectiveif for everymonomorphism $f:X\to Y$ and everymorphism $g:X\to Q$ there exists a morphism $h:Y\to Q$ extending $g$ to $Y$ ,i.e. such that $h\circ f=g$ .^[1]

That is, every morphism $X\to Q$ factors through every monomorphism $X\hookrightarrow Y$ .

The morphism $h$ in the above definition is not required to be uniquely determined by $f$ and $g$ .

In alocally smallcategory, it is equivalent to require that thehom functor $\operatorname {Hom} _{\mathbf {C} }(-,Q)$ carries monomorphisms in $\mathbf {C}$ tosurjectiveset maps.

In Abelian categories

The notion of injectivity was first formulated forabelian categories,and this is still one of its primary areas of application. When $\mathbf {C}$ is an abelian category, an objectQof $\mathbf {C}$ is injectiveif and only ifitshom functorHom_C(–,Q) isexact.

If $0\to Q\to U\to V\to 0$ is anexact sequencein $\mathbf {C}$ such thatQis injective, then thesequence splits.

Enough injectives and injective hulls

The category $\mathbf {C}$ is said tohave enough injectivesif for every objectXof $\mathbf {C}$ ,there exists a monomorphism fromXto an injective object.

A monomorphismgin $\mathbf {C}$ is called anessential monomorphismif for any morphismf,the compositefgis a monomorphism only iffis a monomorphism.

Ifgis an essential monomorphism with domainXand an injective codomainG,thenGis called aninjective hullofX.The injective hull is then uniquely determined byXup toa non-canonical isomorphism.^[1]

Examples

In the category ofabelian groupsandgroup homomorphisms,Ab,an injective object is necessarily adivisible group.Assuming the axiom of choice, the notions are equivalent.
In the category of (left)modulesandmodule homomorphisms,R-Mod,an injective object is aninjective module.R-Modhasinjective hulls(as a consequence,R-Modhas enough injectives).
In thecategory of metric spaces,Met,an injective object is aninjective metric space,and the injective hull of a metric space is itstight span.
In the category ofT₀spacesandcontinuous mappings,an injective object is always aScott topologyon acontinuous lattice,and therefore it is alwayssoberandlocally compact.

Uses

If an abelian category has enough injectives, we can forminjective resolutions,i.e. for a given objectXwe can form a long exact sequence

0\to X\to Q^{0}\to Q^{1}\to Q^{2}\to \cdots

and one can then define thederived functorsof a given functorFby applyingFto this sequence and computing the homology of the resulting (not necessarily exact) sequence. This approach is used to defineExt,andTorfunctors and also the variouscohomologytheories ingroup theory,algebraic topologyandalgebraic geometry.The categories being used are typicallyfunctor categoriesor categories ofsheaves ofO_Xmodulesover someringed space(X,O_X) or, more generally, anyGrothendieck category.

Generalization

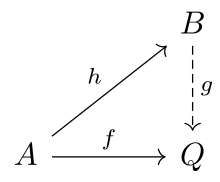
Let $\mathbf {C}$ be a category and let ${\mathcal {H}}$ be aclassof morphisms of $\mathbf {C}$ .

An object $Q$ of $\mathbf {C}$ is said to be ${\mathcal {H}}$ -injectiveif for every morphism $f:A\to Q$ and every morphism $h:A\to B$ in ${\mathcal {H}}$ there exists a morphism $g:B\to Q$ with $g\circ h=f$ .

If ${\mathcal {H}}$ is the class ofmonomorphisms,we are back to the injective objects that were treated above.

The category $\mathbf {C}$ is said tohave enough ${\mathcal {H}}$ -injectivesif for every objectXof $\mathbf {C}$ ,there exists an ${\mathcal {H}}$ -morphism fromXto an ${\mathcal {H}}$ -injective object.

A ${\mathcal {H}}$ -morphismgin $\mathbf {C}$ is called ${\mathcal {H}}$ -essentialif for any morphismf,the compositefgis in ${\mathcal {H}}$ only iffis in ${\mathcal {H}}$ .

Ifgis a ${\mathcal {H}}$ -essential morphism with domainXand an ${\mathcal {H}}$ -injective codomainG,thenGis called an ${\mathcal {H}}$ -injective hullofX.^[1]

Examples of $H$ -injective objects

In the category ofsimplicial sets,the injective objects with respect to the class ${\mathcal {H}}$ of anodyne extensions areKan complexes.
In the category ofpartially ordered setsandmonotone maps,thecomplete latticesform the injective objects for the class ${\mathcal {H}}$ oforder-embeddings,and theDedekind–MacNeille completionof a partially ordered set is its ${\mathcal {H}}$ -injective hull.

Notes

^^a ^b ^cAdamek, Jiri; Herrlich, Horst; Strecker, George (1990). "Sec. 9. Injective objects and essential embeddings".Abstract and Concrete Categories: The Joy of Cats(PDF).Reprints in Theory and Applications of Categories, No. 17 (2006) pp. 1-507. orig. John Wiley. pp. 147–155.

References

Jiri Adamek, Horst Herrlich, George Strecker. Abstract and concrete categories: The joy of cats, Chapter 9, Injective Objects and Essential Embeddings,Republished in Reprints and Applications of Categories, No. 17 (2006) pp. 1-507,Wiley (1990).
J. Rosicky, Injectivity and accessible categories
F. Cagliari and S. Montovani, T₀-reflection and injective hulls of fibre spaces

[:0-1] Adamek, Jiri; Herrlich, Horst; Strecker, George (1990). "Sec. 9. Injective objects and essential embeddings".Abstract and Concrete Categories: The Joy of Cats(PDF).Reprints in Theory and Applications of Categories, No. 17 (2006) pp. 1-507. orig. John Wiley. pp. 147–155.

[1]