Klein bottle

A two-dimensional representation of the Klein bottleimmersedin three-dimensional space

Inmathematics,theKlein bottle(/ˈklaɪn/) is an example of anon-orientablesurface;that is, informally, a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down. More formally, the Klein bottle is atwo-dimensionalmanifoldon which one cannot define anormal vectorat each point that variescontinuouslyover the whole manifold. Other related non-orientable surfaces include theMöbius stripand thereal projective plane.While a Möbius strip is a surface with aboundary,a Klein bottle has no boundary. For comparison, asphereis an orientable surface with no boundary.

The Klein bottle was first described in 1882 by the mathematicianFelix Klein.

Construction

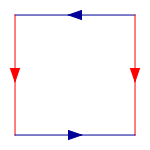
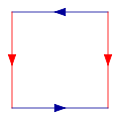
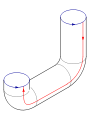
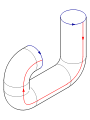
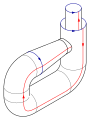
The following square is afundamental polygonof the Klein bottle. The idea is to 'glue' together the corresponding red and blue edges with the arrows matching, as in the diagrams below. Note that this is an "abstract" gluing in the sense that trying to realize this in three dimensions results in a self-intersecting Klein bottle.

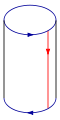
To construct the Klein bottle, glue the red arrows of the square together (left and right sides), resulting in a cylinder. To glue the ends of the cylinder together so that the arrows on the circles match, one would pass one end through the side of the cylinder. This creates a curve of self-intersection; this is thus animmersionof the Klein bottle in thethree-dimensional space.

• 
• 
• 
• 
• 
• 

This immersion is useful for visualizing many properties of the Klein bottle. For example, the Klein bottle has noboundary,where the surface stops abruptly, and it isnon-orientable,as reflected in the one-sidedness of the immersion.

Immersed Klein bottles in theScience Museum in London

A hand-blown Klein Bottle

The common physical model of a Klein bottle is a similar construction. TheScience Museum in Londonhas a collection of hand-blown glass Klein bottles on display, exhibiting many variations on this topological theme. The bottles date from 1995 and were made for the museum by Alan Bennett.

The Klein bottle, proper, does not self-intersect. Nonetheless, there is a way to visualize the Klein bottle as being contained in four dimensions. By adding a fourth dimension to the three-dimensional space, the self-intersection can be eliminated. Gently push a piece of the tube containing the intersection along the fourth dimension, out of the original three-dimensional space. A useful analogy is to consider a self-intersecting curve on the plane; self-intersections can be eliminated by lifting one strand off the plane.

Time evolutionof a Klein figure inxyzt-space

Suppose for clarification that we adopt time as that fourth dimension. Consider how the figure could be constructed inxyzt-space. The accompanying illustration ( "Time evolution..." ) shows one useful evolution of the figure. Att= 0the wall sprouts from a bud somewhere near the "intersection" point. After the figure has grown for a while, the earliest section of the wall begins to recede, disappearing like theCheshire Catbut leaving its ever-expanding smile behind. By the time the growth front gets to where the bud had been, there is nothing there to intersect and the growth completes without piercing existing structure. The 4-figure as defined cannot exist in 3-space but is easily understood in 4-space.

More formally, the Klein bottle is thequotient spacedescribed as thesquare[0,1] × [0,1] with sides identified by the relations(0,y) ~ (1,y)for0 ≤y≤ 1and(x,0) ~ (1 −x,1)for0 ≤x≤ 1.

Properties

Like theMöbius strip,the Klein bottle is a two-dimensionalmanifoldwhich is notorientable.Unlike the Möbius strip, it is aclosedmanifold, meaning it is acompactmanifold without boundary. While the Möbius strip can be embedded in three-dimensionalEuclidean spaceR³,the Klein bottle cannot. It can be embedded inR⁴,however.

Continuing this sequence, for example creating a 3-manifold which cannot be embedded inR⁴but can be inR⁵,is possible; in this case, connecting two ends of aspherinderto each other in the same manner as the two ends of a cylinder for a Klein bottle, creates a figure, referred to as a "spherinder Klein bottle", that cannot fully be embedded inR⁴.

The Klein bottle can be seen as afiber bundleover thecircleS¹,with fibreS¹,as follows: one takes the square (modulo the edge identifying equivalence relation) from above to beE,the total space, while the base spaceBis given by the unit interval iny,modulo1~0.The projection π:E→Bis then given byπ([x,y]) = [y].

The Klein bottle can be constructed (in a four dimensional space, because in three dimensional space it cannot be done without allowing the surface to intersect itself) by joining the edges of two Möbius strips, as described in the followinglimerickbyLeo Moser:

A mathematician namedKlein
Thought the Möbius band was divine.
Said he: "If you glue
The edges of two,
You'll get a weird bottle like mine. "

The initial construction of the Klein bottle by identifying opposite edges of a square shows that the Klein bottle can be given aCW complexstructure with one 0-cellP,two 1-cellsC₁,C₂and one 2-cellD.ItsEuler characteristicis therefore1 − 2 + 1 = 0.The boundary homomorphism is given by∂D= 2C₁and∂C₁= ∂C₂= 0,yielding thehomology groupsof the Klein bottleKto beH₀(K,Z) =Z,H₁(K,Z) =Z×(Z/2Z)andH_n(K,Z) = 0forn> 1.

There is a 2-1covering mapfrom thetorusto the Klein bottle, because two copies of thefundamental regionof the Klein bottle, one being placed next to the mirror image of the other, yield a fundamental region of the torus. Theuniversal coverof both the torus and the Klein bottle is the planeR².

Thefundamental groupof the Klein bottle can be determined as thegroup of deck transformationsof the universal cover and has thepresentation⟨a,b|ab=b⁻¹a⟩.It follows that it is isomorphic to$\mathbb {Z} \rtimes \mathbb {Z}$,the only nontrivial semidirect product of the additive group of integers$\mathbb {Z}$with itself.

A 6-colored Klein bottle, the only exception to the Heawood conjecture

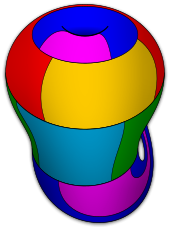
Six colors suffice to color any map on the surface of a Klein bottle; this is the only exception to theHeawood conjecture,a generalization of thefour color theorem,which would require seven.

A Klein bottle is homeomorphic to theconnected sumof twoprojective planes.It is also homeomorphic to a sphere plus twocross-caps.

When embedded in Euclidean space, the Klein bottle is one-sided. However, there are other topological 3-spaces, and in some of the non-orientable examples a Klein bottle can be embedded such that it is two-sided, though due to the nature of the space it remains non-orientable.

Dissection

Dissecting the Klein bottle results in Möbius strips.

Dissecting a Klein bottle into halves along itsplane of symmetryresults in two mirror imageMöbius strips,i.e. one with a left-handed half-twist and the other with a right-handed half-twist (one of these is pictured on the right). Remember that the intersection pictured is not really there.

Simple-closed curves

One description of the types of simple-closed curves that may appear on the surface of the Klein bottle is given by the use of the first homology group of the Klein bottle calculated with integer coefficients. This group is isomorphic toZ×Z₂.Up to reversal of orientation, the only homology classes which contain simple-closed curves are as follows: (0,0), (1,0), (1,1), (2,0), (0,1). Up to reversal of the orientation of a simple closed curve, if it lies within one of the two cross-caps that make up the Klein bottle, then it is in homology class (1,0) or (1,1); if it cuts the Klein bottle into two Möbius strips, then it is in homology class (2,0); if it cuts the Klein bottle into an annulus, then it is in homology class (0,1); and if bounds a disk, then it is in homology class (0,0).

Parametrization

The "figure 8" immersion of the Klein bottle.

Klein bagel cross section, showing a figure eight curve (thelemniscate of Gerono).

The figure 8 immersion

To make the "figure 8" or "bagel"immersionof the Klein bottle, one can start with aMöbius stripand curl it to bring the edge to the midline; since there is only one edge, it will meet itself there, passing through the midline. It has a particularly simple parametrization as a "figure-8" torus with a half-twist:

${\begin{aligned}x&=\left(r+\cos {\frac {\theta }{2}}\sin v-\sin {\frac {\theta }{2}}\sin 2v\right)\cos \theta \\y&=\left(r+\cos {\frac {\theta }{2}}\sin v-\sin {\frac {\theta }{2}}\sin 2v\right)\sin \theta \\z&=\sin {\frac {\theta }{2}}\sin v+\cos {\frac {\theta }{2}}\sin 2v\end{aligned}}$

for 0 ≤θ< 2π, 0 ≤v< 2π andr> 2.

In this immersion, the self-intersection circle (where sin(v) is zero) is a geometriccirclein thexyplane. The positive constantris the radius of this circle. The parameterθgives the angle in thexyplane as well as the rotation of the figure 8, andvspecifies the position around the 8-shaped cross section. With the above parametrization the cross section is a 2:1Lissajous curve.

4-D non-intersecting

A non-intersecting 4-D parametrization can be modeled after that of theflat torus:

${\begin{aligned}x&=R\left(\cos {\frac {\theta }{2}}\cos v-\sin {\frac {\theta }{2}}\sin 2v\right)\\y&=R\left(\sin {\frac {\theta }{2}}\cos v+\cos {\frac {\theta }{2}}\sin 2v\right)\\z&=P\cos \theta \left(1+\varepsilon \sin v\right)\\w&=P\sin \theta \left(1+{\varepsilon }\sin v\right)\end{aligned}}$

whereRandPare constants that determine aspect ratio,θandvare similar to as defined above.vdetermines the position around the figure-8 as well as the position in the x-y plane.θdetermines the rotational angle of the figure-8 as well and the position around the z-w plane.εis any small constant andεsinvis a smallvdependent bump inz-wspace to avoid self intersection. Thevbump causes the self intersecting 2-D/planar figure-8 to spread out into a 3-D stylized "potato chip" or saddle shape in the x-y-w and x-y-z space viewed edge on. Whenε=0the self intersection is a circle in the z-w plane <0, 0, cosθ,sinθ>.

3D pinched torus / 4D Möbius tube

The pinched torus immersion of the Klein bottle.

The pinched torus is perhaps the simplest parametrization of the klein bottle in both three and four dimensions. It's a torus that, in three dimensions, flattens and passes through itself on one side. Unfortunately, in three dimensions this parametrization has twopinch points,which makes it undesirable for some applications. In four dimensions thezamplitude rotates into thewamplitude and there are no self intersections or pinch points.

${\begin{aligned}x(\theta,\varphi )&=(R+r\cos \theta )\cos {\varphi }\\y(\theta,\varphi )&=(R+r\cos \theta )\sin {\varphi }\\z(\theta,\varphi )&=r\sin \theta \cos \left({\frac {\varphi }{2}}\right)\\w(\theta,\varphi )&=r\sin \theta \sin \left({\frac {\varphi }{2}}\right)\end{aligned}}$

One can view this as a tube or cylinder that wraps around, as in a torus, but its circular cross section flips over in four dimensions, presenting its "backside" as it reconnects, just as a Möbius strip cross section rotates before it reconnects. The 3D orthogonal projection of this is the pinched torus shown above. Just as a Möbius strip is a subset of a solid torus, the Möbius tube is a subset of a toroidally closedspherinder(solidspheritorus).

Bottle shape

The parametrization of the 3-dimensional immersion of the bottle itself is much more complicated.

Klein Bottle with slight transparency

${\begin{aligned}x(u,v)=-&{\frac {2}{15}}\cos u\left(3\cos {v}-30\sin {u}+90\cos ^{4}{u}\sin {u}\right.-\\&\left.60\cos ^{6}{u}\sin {u}+5\cos {u}\cos {v}\sin {u}\right)\\[3pt]y(u,v)=-&{\frac {1}{15}}\sin u\left(3\cos {v}-3\cos ^{2}{u}\cos {v}-48\cos ^{4}{u}\cos {v}+48\cos ^{6}{u}\cos {v}\right.-\\&60\sin {u}+5\cos {u}\cos {v}\sin {u}-5\cos ^{3}{u}\cos {v}\sin {u}-\\&\left.80\cos ^{5}{u}\cos {v}\sin {u}+80\cos ^{7}{u}\cos {v}\sin {u}\right)\\[3pt]z(u,v)=&{\frac {2}{15}}\left(3+5\cos {u}\sin {u}\right)\sin {v}\end{aligned}}$

for 0 ≤u< π and 0 ≤v< 2π.

Homotopy classes

Regular 3D immersions of the Klein bottle fall into threeregular homotopyclasses. The three are represented by:

• the "traditional" Klein bottle;
• the left-handed figure-8 Klein bottle;
• the right-handed figure-8 Klein bottle.

The traditional Klein bottle immersion isachiral.The figure-8 immersion is chiral. (The pinched torus immersion above is not regular, as it has pinch points, so it is not relevant to this section.)

If the traditional Klein bottle is cut in its plane of symmetry it breaks into two Möbius strips of opposite chirality. A figure-8 Klein bottle can be cut into two Möbius strips of thesamechirality, and cannot be regularly deformed into its mirror image.

Generalizations

The generalization of the Klein bottle to highergenusis given in the article on thefundamental polygon.

In another order of ideas, constructing3-manifolds,it is known that asolid Klein bottleishomeomorphicto theCartesian productof aMöbius stripand a closed interval. Thesolid Klein bottleis the non-orientable version of thesolid torus,equivalent to$D^{2}\times S^{1}.$

Klein surface

AKlein surfaceis, as forRiemann surfaces,a surface with an atlas allowing thetransition mapsto be composed usingcomplex conjugation.One can obtain the so-calleddianalytic structureof the space and has only one side.

See also

• Algebraic topology
• Alice universe
• Bavard's Klein bottle systolic inequality
• Boy's surface

References

Sources

• This article incorporates material from Klein bottle onPlanetMath,which is licensed under theCreative Commons Attribution/Share-Alike License.
• Weisstein, Eric W."Klein Bottle".MathWorld.
• Alling, Norman; Greenleaf, Newcomb (1969)."Klein surfaces and real algebraic function fields".Bulletin of the American Mathematical Society.75(4): 627–888.doi:10.1090/S0002-9904-1969-12332-3.MR0251213.PEeuclid.bams/1183530665.(A classical on the theory of Klein surfaces)
• Stillwell, John(1993).Classical Topology and Combinatorial Group Theory(2nd ed.).Springer-Verlag.ISBN0-387-97970-0.

External links

• Imaging Maths - The Klein Bottle
• The biggest Klein bottle in all the world
• Klein Bottle animation: produced for a topology seminar at the Leibniz University Hannover.
• Klein Bottle animation from 2010 including a car ride through the bottle and the original description by Felix Klein: produced at the Free University Berlin.
• Klein Bottle,XScreenSaver"hack". A screensaver forX 11andOS Xfeaturing an animated Klein Bottle.