Taylor series

As the degree of the Taylor polynomial rises, it approaches the correct function. This image showssinxand its Taylor approximations by polynomials of degree1,3,5,7,9,11,and13atx= 0.

Inmathematics,theTaylor seriesorTaylor expansionof afunctionis aninfinite sumof terms that are expressed in terms of the function'sderivativesat a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named afterBrook Taylor,who introduced them in 1715. A Taylor series is also called aMaclaurin serieswhen 0 is the point where the derivatives are considered, afterColin Maclaurin,who made extensive use of this special case of Taylor series in the 18th century.

Thepartial sumformed by the firstn+ 1terms of a Taylor series is apolynomialof degreenthat is called thenthTaylor polynomialof the function. Taylor polynomials are approximations of a function, which become generally more accurate asnincreases.Taylor's theoremgives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function isconvergent,its sum is thelimitof theinfinite sequenceof the Taylor polynomials. A function may differ from the sum of its Taylor series, even if its Taylor series is convergent. A function isanalyticat a pointxif it is equal to the sum of its Taylor series in someopen interval(oropen diskin thecomplex plane) containingx.This implies that the function is analytic at every point of the interval (or disk).

Definition

The Taylor series of arealorcomplex-valued functionf (x),that isinfinitely differentiableat arealorcomplex numbera,is thepower series $$f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f'''(a)}{3!}}(x-a)^{3}+\cdots =\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}.$$ Here,n!denotes thefactorialofn.The functionf⁽ⁿ⁾(a)denotes thenthderivativeoffevaluated at the pointa.The derivative of order zero offis defined to befitself and(x−a)⁰and0!are both defined to be 1.This series can be written by usingsigma notation,as in the right side formula.Witha= 0,the Maclaurin series takes the form: $$f(0)+{\frac {f'(0)}{1!}}x+{\frac {f''(0)}{2!}}x^{2}+{\frac {f'''(0)}{3!}}x^{3}+\cdots =\sum _{n=0}^{\infty }{\frac {f^{(n)}(0)}{n!}}x^{n}.$$

Examples

The Taylor series of anypolynomialis the polynomial itself.

The Maclaurin series of⁠1/1 −x⁠is thegeometric series

$$1+x+x^{2}+x^{3}+\cdots.$$

So, by substitutingxfor1 −x,the Taylor series of⁠1/x⁠ata= 1is

$$1-(x-1)+(x-1)^{2}-(x-1)^{3}+\cdots.$$

By integrating the above Maclaurin series, we find the Maclaurin series ofln(1 −x),wherelndenotes thenatural logarithm:

$$-x-{\tfrac {1}{2}}x^{2}-{\tfrac {1}{3}}x^{3}-{\tfrac {1}{4}}x^{4}-\cdots.$$

The corresponding Taylor series oflnxata= 1is

$$(x-1)-{\tfrac {1}{2}}(x-1)^{2}+{\tfrac {1}{3}}(x-1)^{3}-{\tfrac {1}{4}}(x-1)^{4}+\cdots,$$

and more generally, the corresponding Taylor series oflnxat an arbitrary nonzero pointais:

$$\ln a+{\frac {1}{a}}(x-a)-{\frac {1}{a^{2}}}{\frac {\left(x-a\right)^{2}}{2}}+\cdots.$$

The Maclaurin series of theexponential functione^xis

$${\begin{aligned}\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}&={\frac {x^{0}}{0!}}+{\frac {x^{1}}{1!}}+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+{\frac {x^{5}}{5!}}+\cdots \\&=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+{\frac {x^{4}}{24}}+{\frac {x^{5}}{120}}+\cdots.\end{aligned}}$$

The above expansion holds because the derivative ofe^xwith respect toxis alsoe^x,ande⁰equals 1. This leaves the terms(x− 0)ⁿin the numerator andn!in the denominator of each term in the infinite sum.

History

Theancient Greek philosopherZeno of Eleaconsidered the problem of summing an infinite series to achieve a finite result, but rejected it as an impossibility;the result wasZeno's paradox.Later,Aristotleproposed a philosophical resolution of the paradox, but the mathematical content was apparently unresolved until taken up byArchimedes,as it had been prior to Aristotle by the Presocratic AtomistDemocritus.It was through Archimedes'smethod of exhaustionthat an infinite number of progressive subdivisions could be performed to achieve a finite result.Liu Huiindependently employed a similar method a few centuries later.

In the 14th century, the earliest examples of specific Taylor series (but not the general method) were given by Indian mathematicianMadhava of Sangamagrama.Though no record of his work survives, writings of his followers in theKerala school of astronomy and mathematicssuggest that he found the Taylor series for thetrigonometric functionsofsine,cosine,andarctangent(seeMadhava series). During the following two centuries his followers developed further series expansions and rational approximations.

In late 1670,James Gregorywas shown in a letter fromJohn Collinsseveral Maclaurin series(${\textstyle \sin x,}$${\textstyle \cos x,}$${\textstyle \arcsin x,}$and${\textstyle x\cot x}$)derived byIsaac Newton,and told that Newton had developed a general method for expanding functions in series. Newton had in fact used a cumbersome method involving long division of series and term-by-term integration, but Gregory did not know it and set out to discover a general method for himself. In early 1671 Gregory discovered something like the general Maclaurin series and sent a letter to Collins including series for${\textstyle \arctan x,}$${\textstyle \tan x,}$${\textstyle \sec x,}$${\textstyle \ln \,\sec x}$(the integral of$\tan$),${\textstyle \ln \,\tan {\tfrac {1}{2}}{{\bigl (}{\tfrac {1}{2}}\pi +x{\bigr )}}}$(theintegral ofsec,the inverseGudermannian function),${\textstyle \operatorname {arcsec} {\bigl (}{\sqrt {2}}e^{x}{\bigr )},}$and${\textstyle 2\arctan e^{x}-{\tfrac {1}{2}}\pi }$(the Gudermannian function). However, thinking that he had merely redeveloped a method by Newton, Gregory never described how he obtained these series, and it can only be inferred that he understood the general method by examining scratch work he had scribbled on the back of another letter from 1671.

In 1691–1692, Isaac Newton wrote down an explicit statement of the Taylor and Maclaurin series in an unpublished version of his workDe Quadratura Curvarum.However, this work was never completed and the relevant sections were omitted from the portions published in 1704 under the titleTractatus de Quadratura Curvarum.

It was not until 1715 that a general method for constructing these series for all functions for which they exist was finally published byBrook Taylor,after whom the series are now named.

The Maclaurin series was named afterColin Maclaurin,a Scottish mathematician, who published the special case of the Taylor result in the mid-18th century.

Analytic functions

Main article:Analytic function

The functione^(−1/x2)is not analytic atx= 0:the Taylor series is identically 0, although the function is not.

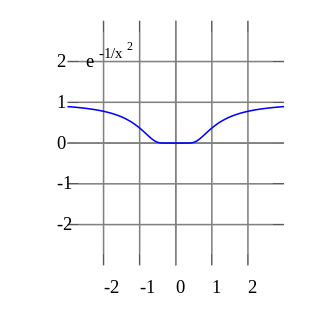
Iff (x)is given by a convergent power series in an open disk centred atbin the complex plane (or an interval in the real line), it is said to beanalyticin this region. Thus forxin this region,fis given by a convergent power series

$$f(x)=\sum _{n=0}^{\infty }a_{n}(x-b)^{n}.$$

Differentiating byxthe above formulantimes, then settingx=bgives:

$${\frac {f^{(n)}(b)}{n!}}=a_{n}$$

and so the power series expansion agrees with the Taylor series. Thus a function is analytic in an open disk centered atbif and only if its Taylor series converges to the value of the function at each point of the disk.

Iff (x)is equal to the sum of its Taylor series for allxin the complex plane, it is calledentire.The polynomials,exponential functione^x,and thetrigonometric functionssine and cosine, are examples of entire functions. Examples of functions that are not entire include thesquare root,thelogarithm,thetrigonometric functiontangent, and its inverse,arctan.For these functions the Taylor series do notconvergeifxis far fromb.That is, the Taylor seriesdivergesatxif the distance betweenxandbis larger than theradius of convergence.The Taylor series can be used to calculate the value of an entire function at every point, if the value of the function, and of all of its derivatives, are known at a single point.

Uses of the Taylor series for analytic functions include:

1. The partial sums (theTaylor polynomials) of the series can be used as approximations of the function. These approximations are good if sufficiently many terms are included.
2. Differentiation and integration of power series can be performed term by term and is hence particularly easy.
3. Ananalytic functionis uniquely extended to aholomorphic functionon an open disk in thecomplex plane.This makes the machinery ofcomplex analysisavailable.
4. The (truncated) series can be used to compute function values numerically, (often by recasting the polynomial into theChebyshev formand evaluating it with theClenshaw algorithm).
5. Algebraic operations can be done readily on the power series representation; for instance,Euler's formulafollows from Taylor series expansions for trigonometric and exponential functions. This result is of fundamental importance in such fields asharmonic analysis.
6. Approximations using the first few terms of a Taylor series can make otherwise unsolvable problems possible for a restricted domain; this approach is often used in physics.

Approximation error and convergence

Main article:Taylor's theorem

The sine function (blue) is closely approximated by its Taylor polynomial of degree 7 (pink) for a full period centered at the origin.

The Taylor polynomials forln(1 +x)only provide accurate approximations in the range−1 <x≤ 1.Forx> 1,Taylor polynomials of higher degree provide worse approximations.

The Taylor approximations forln(1 +x)(black). Forx> 1,the approximations diverge.

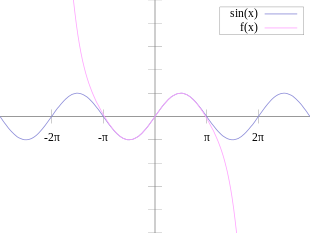
Pictured is an accurate approximation ofsinxaround the pointx= 0.The pink curve is a polynomial of degree seven:

$$\sin {x}\approx x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}.\!$$

The error in this approximation is no more than|x|⁹ / 9!.For a full cycle centered at the origin (−π <x< π) the error is less than 0.08215. In particular, for−1 <x< 1,the error is less than 0.000003.

In contrast, also shown is a picture of the natural logarithm functionln(1 +x)and some of its Taylor polynomials arounda= 0.These approximations converge to the function only in the region−1 <x≤ 1;outside of this region the higher-degree Taylor polynomials areworseapproximations for the function.

Theerrorincurred in approximating a function by itsnth-degree Taylor polynomial is called theremainderorresidualand is denoted by the functionR_n(x).Taylor's theorem can be used to obtain a bound on thesize of the remainder.

In general, Taylor series need not beconvergentat all. In fact, the set of functions with a convergent Taylor series is ameager setin theFréchet spaceofsmooth functions.Even if the Taylor series of a functionfdoes converge, its limit need not be equal to the value of the functionf (x).For example, the function

$$f(x)={\begin{cases}e^{-1/x^{2}}&{\text{if }}x\neq 0\\[3mu]0&{\text{if }}x=0\end{cases}}$$

isinfinitely differentiableatx= 0,and has all derivatives zero there. Consequently, the Taylor series off (x)aboutx= 0is identically zero. However,f (x)is not the zero function, so does not equal its Taylor series around the origin. Thus,f (x)is an example of anon-analytic smooth function.

Inreal analysis,this example shows that there areinfinitely differentiable functionsf (x)whose Taylor series arenotequal tof (x)even if they converge. By contrast, theholomorphic functionsstudied incomplex analysisalways possess a convergent Taylor series, and even the Taylor series ofmeromorphic functions,which might have singularities, never converge to a value different from the function itself. The complex functione^−1/z2,however, does not approach 0 whenzapproaches 0 along the imaginary axis, so it is notcontinuousin the complex plane and its Taylor series is undefined at 0.

More generally, every sequence of real or complex numbers can appear ascoefficientsin the Taylor series of an infinitely differentiable function defined on the real line, a consequence ofBorel's lemma.As a result, theradius of convergenceof a Taylor series can be zero. There are even infinitely differentiable functions defined on the real line whose Taylor series have a radius of convergence 0 everywhere.

A function cannot be written as a Taylor series centred at asingularity;in these cases, one can often still achieve a series expansion if one allows also negative powers of the variablex;seeLaurent series.For example,f (x) =e^−1/x2can be written as a Laurent series.

Generalization

The generalization of the Taylor series does converge to the value of the function itself for anyboundedcontinuous functionon(0,∞),and this can be done by using the calculus offinite differences.Specifically, the following theorem, due toEinar Hille,that for anyt> 0,

$$\lim _{h\to 0^{+}}\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}{\frac {\Delta _{h}^{n}f(a)}{h^{n}}}=f(a+t).$$

HereΔⁿ
_his thenth finite difference operator with step sizeh.The series is precisely the Taylor series, except that divided differences appear in place of differentiation: the series is formally similar to theNewton series.When the functionfis analytic ata,the terms in the series converge to the terms of the Taylor series, and in this sense generalizes the usual Taylor series.

In general, for any infinite sequencea_i,the following power series identity holds:

$$\sum _{n=0}^{\infty }{\frac {u^{n}}{n!}}\Delta ^{n}a_{i}=e^{-u}\sum _{j=0}^{\infty }{\frac {u^{j}}{j!}}a_{i+j}.$$

So in particular,

$$f(a+t)=\lim _{h\to 0^{+}}e^{-t/h}\sum _{j=0}^{\infty }f(a+jh){\frac {(t/h)^{j}}{j!}}.$$

The series on the right is theexpected valueoff (a+X),whereXis aPoisson-distributedrandom variablethat takes the valuejhwith probabilitye^−t/h·⁠(t/h)^j/j!⁠.Hence,

$$f(a+t)=\lim _{h\to 0^{+}}\int _{-\infty }^{\infty }f(a+x)dP_{t/h,h}(x).$$

Thelaw of large numbersimplies that the identity holds.

List of Maclaurin series of some common functions

See also:List of mathematical series

Several important Maclaurin series expansions follow. All these expansions are valid for complex argumentsx.

Exponential function

Theexponential functione^x(in blue), and the sum of the firstn+ 1terms of its Taylor series at 0 (in red).

Theexponential function$e^{x}$(with basee) has Maclaurin series

$$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots.$$ It converges for allx.

The exponentialgenerating functionof theBell numbersis the exponential function of the predecessor of the exponential function:

$$\exp(\exp {x}-1)=\sum _{n=0}^{\infty }{\frac {B_{n}}{n!}}x^{n}$$

Natural logarithm

Thenatural logarithm(with basee) has Maclaurin series

$${\begin{aligned}\ln(1-x)&=-\sum _{n=1}^{\infty }{\frac {x^{n}}{n}}=-x-{\frac {x^{2}}{2}}-{\frac {x^{3}}{3}}-\cdots,\\\ln(1+x)&=\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {x^{n}}{n}}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots.\end{aligned}}$$

The last series is known asMercator series,named afterNicholas Mercator(since it was published in his 1668 treatiseLogarithmotechnia).Both of these series converge for$|x|<1$.(In addition, the series forln(1 −x)converges forx= −1,and the series forln(1 +x)converges forx= 1.)

Geometric series

Thegeometric seriesand its derivatives have Maclaurin series

$${\begin{aligned}{\frac {1}{1-x}}&=\sum _{n=0}^{\infty }x^{n}\\{\frac {1}{(1-x)^{2}}}&=\sum _{n=1}^{\infty }nx^{n-1}\\{\frac {1}{(1-x)^{3}}}&=\sum _{n=2}^{\infty }{\frac {(n-1)n}{2}}x^{n-2}.\end{aligned}}$$

All are convergent for$|x|<1$.These are special cases of thebinomial seriesgiven in the next section.

Binomial series

Thebinomial seriesis the power series

$$(1+x)^{\ Alpha }=\sum _{n=0}^{\infty }{\binom {\ Alpha }{n}}x^{n}$$

whose coefficients are the generalizedbinomial coefficients

$${\binom {\ Alpha }{n}}=\prod _{k=1}^{n}{\frac {\ Alpha -k+1}{k}}={\frac {\ Alpha (\ Alpha -1)\cdots (\ Alpha -n+1)}{n!}}.$$

(Ifn= 0,this product is anempty productand has value 1.) It converges for$|x|<1$for any real or complex numberα.

Whenα= −1,this is essentially the infinite geometric series mentioned in the previous section. The special casesα=⁠1/2⁠andα= −⁠1/2⁠give thesquare rootfunction and itsinverse:

$${\begin{aligned}(1+x)^{\frac {1}{2}}&=1+{\frac {1}{2}}x-{\frac {1}{8}}x^{2}+{\frac {1}{16}}x^{3}-{\frac {5}{128}}x^{4}+{\frac {7}{256}}x^{5}-\cdots &=\sum _{n=0}^{\infty }{\frac {(-1)^{n-1}(2n)!}{4^{n}(n!)^{2}(2n-1)}}x^{n},\\(1+x)^{-{\frac {1}{2}}}&=1-{\frac {1}{2}}x+{\frac {3}{8}}x^{2}-{\frac {5}{16}}x^{3}+{\frac {35}{128}}x^{4}-{\frac {63}{256}}x^{5}+\cdots &=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}}}x^{n}.\end{aligned}}$$

When only thelinear termis retained, this simplifies to thebinomial approximation.

Trigonometric functions

The usualtrigonometric functionsand their inverses have the following Maclaurin series:

$${\begin{aligned}\sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}&&=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots &&{\text{for all }}x\\[6pt]\cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}&&=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots &&{\text{for all }}x\\[6pt]\tan x&=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}\left(1-4^{n}\right)}{(2n)!}}x^{2n-1}&&=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\sec x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}E_{2n}}{(2n)!}}x^{2n}&&=1+{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\arcsin x&=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x+{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}+\cdots &&{\text{for }}|x|\leq 1\\[6pt]\arccos x&={\frac {\pi }{2}}-\arcsin x\\&={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&={\frac {\pi }{2}}-x-{\frac {x^{3}}{6}}-{\frac {3x^{5}}{40}}-\cdots &&{\text{for }}|x|\leq 1\\[6pt]\arctan x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}&&=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm i\end{aligned}}$$

All angles are expressed inradians.The numbersB_kappearing in the expansions oftanxare theBernoulli numbers.TheE_kin the expansion ofsecxareEuler numbers.

Hyperbolic functions

Thehyperbolic functionshave Maclaurin series closely related to the series for the corresponding trigonometric functions:

$${\begin{aligned}\sinh x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}&&=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+\cdots &&{\text{for all }}x\\[6pt]\cosh x&=\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}&&=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+\cdots &&{\text{for all }}x\\[6pt]\tanh x&=\sum _{n=1}^{\infty }{\frac {B_{2n}4^{n}\left(4^{n}-1\right)}{(2n)!}}x^{2n-1}&&=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots &&{\text{for }}|x|<{\frac {\pi }{2}}\\[6pt]\operatorname {arsinh} x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}&&=x-{\frac {x^{3}}{6}}+{\frac {3x^{5}}{40}}-\cdots &&{\text{for }}|x|\leq 1\\[6pt]\operatorname {artanh} x&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}}&&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+\cdots &&{\text{for }}|x|\leq 1,\ x\neq \pm 1\end{aligned}}$$

The numbersB_kappearing in the series fortanhxare theBernoulli numbers.

Polylogarithmic functions

Thepolylogarithmshave these defining identities:

$${\begin{aligned}{\text{Li}}_{2}(x)&=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}x^{n}\\{\text{Li}}_{3}(x)&=\sum _{n=1}^{\infty }{\frac {1}{n^{3}}}x^{n}\end{aligned}}$$

TheLegendre chi functionsare defined as follows:

$${\begin{aligned}\chi _{2}(x)&=\sum _{n=0}^{\infty }{\frac {1}{(2n+1)^{2}}}x^{2n+1}\\\chi _{3}(x)&=\sum _{n=0}^{\infty }{\frac {1}{(2n+1)^{3}}}x^{2n+1}\end{aligned}}$$

And the formulas presented below are calledinverse tangent integrals:

$${\begin{aligned}{\text{Ti}}_{2}(x)&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)^{2}}}x^{2n+1}\\{\text{Ti}}_{3}(x)&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)^{3}}}x^{2n+1}\end{aligned}}$$

Instatistical thermodynamicsthese formulas are of great importance.

Elliptic functions

The completeelliptic integralsof first kind K and of second kind E can be defined as follows:

$${\begin{aligned}{\frac {2}{\pi }}K(x)&=\sum _{n=0}^{\infty }{\frac {[(2n)!]^{2}}{16^{n}(n!)^{4}}}x^{2n}\\{\frac {2}{\pi }}E(x)&=\sum _{n=0}^{\infty }{\frac {[(2n)!]^{2}}{(1-2n)16^{n}(n!)^{4}}}x^{2n}\end{aligned}}$$

TheJacobi theta functionsdescribe the world of the elliptic modular functions and they have these Taylor series:

$${\begin{aligned}\vartheta _{00}(x)&=1+2\sum _{n=1}^{\infty }x^{n^{2}}\\\vartheta _{01}(x)&=1+2\sum _{n=1}^{\infty }(-1)^{n}x^{n^{2}}\end{aligned}}$$

The regularpartition number sequenceP(n) has this generating function:

$$\vartheta _{00}(x)^{-1/6}\vartheta _{01}(x)^{-2/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{-1/24}=\sum _{n=0}^{\infty }P(n)x^{n}=\prod _{k=1}^{\infty }{\frac {1}{1-x^{k}}}$$

The strict partition number sequence Q(n) has that generating function:

$$\vartheta _{00}(x)^{1/6}\vartheta _{01}(x)^{-1/3}{\biggl [}{\frac {\vartheta _{00}(x)^{4}-\vartheta _{01}(x)^{4}}{16\,x}}{\biggr ]}^{1/24}=\sum _{n=0}^{\infty }Q(n)x^{n}=\prod _{k=1}^{\infty }{\frac {1}{1-x^{2k-1}}}$$

Calculation of Taylor series

Several methods exist for the calculation of Taylor series of a large number of functions. One can attempt to use the definition of the Taylor series, though this often requires generalizing the form of the coefficients according to a readily apparent pattern. Alternatively, one can use manipulations such as substitution, multiplication or division, addition or subtraction of standard Taylor series to construct the Taylor series of a function, by virtue of Taylor series being power series. In some cases, one can also derive the Taylor series by repeatedly applyingintegration by parts.Particularly convenient is the use ofcomputer algebra systemsto calculate Taylor series.

First example

In order to compute the 7th degree Maclaurin polynomial for the function

$$f(x)=\ln(\cos x),\quad x\in {\bigl (}{-{\tfrac {\pi }{2}}},{\tfrac {\pi }{2}}{\bigr )},$$

one may first rewrite the function as

$$f(x)={\ln }{\bigl (}1+(\cos x-1){\bigr )},$$

the composition of two functions$x\mapsto \ln(1+x)$and$x\mapsto \cos x-1.$The Taylor series for the natural logarithm is (usingbig O notation)

$$\ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}+O{\left(x^{4}\right)}$$

and for the cosine function

$$\cos x-1=-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-{\frac {x^{6}}{720}}+O{\left(x^{8}\right)}.$$

The first several terms from the second series can be substituted into each term of the first series. Because the first term in the second series has degree 2, three terms of the first series suffice to give a 7th-degree polynomial:

$${\begin{aligned}f(x)&=\ln {\bigl (}1+(\cos x-1){\bigr )}\\&=(\cos x-1)-{\tfrac {1}{2}}(\cos x-1)^{2}+{\tfrac {1}{3}}(\cos x-1)^{3}+O{\left((\cos x-1)^{4}\right)}\\&=-{\frac {x^{2}}{2}}-{\frac {x^{4}}{12}}-{\frac {x^{6}}{45}}+O{\left(x^{8}\right)}.\end{aligned}}\!$$

Since the cosine is aneven function,the coefficients for all the odd powers are zero.

Second example

Suppose we want the Taylor series at 0 of the function

$$g(x)={\frac {e^{x}}{\cos x}}.\!$$

The Taylor series for the exponential function is

$$e^{x}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots,$$

and the series for cosine is

$$\cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots.$$

Assume the series for their quotient is

$${\frac {e^{x}}{\cos x}}=c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+c_{4}x^{4}+\cdots$$

Multiplying both sides by the denominator$\cos x$and then expanding it as a series yields

$${\begin{aligned}e^{x}&=\left(c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+c_{4}x^{4}+\cdots \right)\left(1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots \right)\\[5mu]&=c_{0}+c_{1}x+\left(c_{2}-{\frac {c_{0}}{2}}\right)x^{2}+\left(c_{3}-{\frac {c_{1}}{2}}\right)x^{3}+\left(c_{4}-{\frac {c_{2}}{2}}+{\frac {c_{0}}{4!}}\right)x^{4}+\cdots \end{aligned}}$$

Comparing the coefficients of$g(x)\cos x$with the coefficients of$e^{x},$

$$c_{0}=1,\ \ c_{1}=1,\ \ c_{2}-{\tfrac {1}{2}}c_{0}={\tfrac {1}{2}},\ \ c_{3}-{\tfrac {1}{2}}c_{1}={\tfrac {1}{6}},\ \ c_{4}-{\tfrac {1}{2}}c_{2}+{\tfrac {1}{24}}c_{0}={\tfrac {1}{24}},\ \ldots.$$

The coefficients$c_{i}$of the series for$g(x)$can thus be computed one at a time, amounting to long division of the series for$e^{x}$and$\cos x$:

$${\frac {e^{x}}{\cos x}}=1+x+x^{2}+{\tfrac {2}{3}}x^{3}+{\tfrac {1}{2}}x^{4}+\cdots.$$

Third example

Here we employ a method called "indirect expansion" to expand the given function. This method uses the known Taylor expansion of the exponential function. In order to expand(1 +x)e^xas a Taylor series inx,we use the known Taylor series of functione^x:

$$e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots.$$

Thus,

$${\begin{aligned}(1+x)e^{x}&=e^{x}+xe^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=0}^{\infty }{\frac {x^{n+1}}{n!}}=1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=0}^{\infty }{\frac {x^{n+1}}{n!}}\\&=1+\sum _{n=1}^{\infty }{\frac {x^{n}}{n!}}+\sum _{n=1}^{\infty }{\frac {x^{n}}{(n-1)!}}=1+\sum _{n=1}^{\infty }\left({\frac {1}{n!}}+{\frac {1}{(n-1)!}}\right)x^{n}\\&=1+\sum _{n=1}^{\infty }{\frac {n+1}{n!}}x^{n}\\&=\sum _{n=0}^{\infty }{\frac {n+1}{n!}}x^{n}.\end{aligned}}$$

Taylor series as definitions

Classically,algebraic functionsare defined by an algebraic equation, andtranscendental functions(including those discussed above) are defined by some property that holds for them, such as adifferential equation.For example, theexponential functionis the function which is equal to its own derivative everywhere, and assumes the value 1 at the origin. However, one may equally well define ananalytic functionby its Taylor series.

Taylor series are used to define functions and "operators"in diverse areas of mathematics. In particular, this is true in areas where the classical definitions of functions break down. For example, using Taylor series, one may extend analytic functions to sets of matrices and operators, such as thematrix exponentialormatrix logarithm.

In other areas, such as formal analysis, it is more convenient to work directly with thepower seriesthemselves. Thus one may define a solution of a differential equationasa power series which, one hopes to prove, is the Taylor series of the desired solution.

Taylor series in several variables

The Taylor series may also be generalized to functions of more than one variable with

$${\begin{aligned}T(x_{1},\ldots,x_{d})&=\sum _{n_{1}=0}^{\infty }\cdots \sum _{n_{d}=0}^{\infty }{\frac {(x_{1}-a_{1})^{n_{1}}\cdots (x_{d}-a_{d})^{n_{d}}}{n_{1}!\cdots n_{d}!}}\,\left({\frac {\partial ^{n_{1}+\cdots +n_{d}}f}{\partial x_{1}^{n_{1}}\cdots \partial x_{d}^{n_{d}}}}\right)(a_{1},\ldots,a_{d})\\&=f(a_{1},\ldots,a_{d})+\sum _{j=1}^{d}{\frac {\partial f(a_{1},\ldots,a_{d})}{\partial x_{j}}}(x_{j}-a_{j})+{\frac {1}{2!}}\sum _{j=1}^{d}\sum _{k=1}^{d}{\frac {\partial ^{2}f(a_{1},\ldots,a_{d})}{\partial x_{j}\partial x_{k}}}(x_{j}-a_{j})(x_{k}-a_{k})\\&\qquad \qquad +{\frac {1}{3!}}\sum _{j=1}^{d}\sum _{k=1}^{d}\sum _{l=1}^{d}{\frac {\partial ^{3}f(a_{1},\ldots,a_{d})}{\partial x_{j}\partial x_{k}\partial x_{l}}}(x_{j}-a_{j})(x_{k}-a_{k})(x_{l}-a_{l})+\cdots \end{aligned}}$$

For example, for a function$f(x,y)$that depends on two variables,xandy,the Taylor series to second order about the point(a,b)is

$$f(a,b)+(x-a)f_{x}(a,b)+(y-b)f_{y}(a,b)+{\frac {1}{2!}}{\Big (}(x-a)^{2}f_{xx}(a,b)+2(x-a)(y-b)f_{xy}(a,b)+(y-b)^{2}f_{yy}(a,b){\Big )}$$

where the subscripts denote the respectivepartial derivatives.

Second-order Taylor series in several variables

See also:Linearization § Multivariable functions

A second-order Taylor series expansion of a scalar-valued function of more than one variable can be written compactly as

$$T(\mathbf {x} )=f(\mathbf {a} )+(\mathbf {x} -\mathbf {a} )^{\mathsf {T}}Df(\mathbf {a} )+{\frac {1}{2!}}(\mathbf {x} -\mathbf {a} )^{\mathsf {T}}\left\{D^{2}f(\mathbf {a} )\right\}(\mathbf {x} -\mathbf {a} )+\cdots,$$

whereDf (a)is thegradientoffevaluated atx=aandD²f (a)is theHessian matrix.Applying themulti-index notationthe Taylor series for several variables becomes

$$T(\mathbf {x} )=\sum _{|\ Alpha |\geq 0}{\frac {(\mathbf {x} -\mathbf {a} )^{\ Alpha }}{\ Alpha!}}\left({\mathrm {\partial } ^{\ Alpha }}f\right)(\mathbf {a} ),$$

which is to be understood as a still more abbreviatedmulti-indexversion of the first equation of this paragraph, with a full analogy to the single variable case.

Example

Second-order Taylor series approximation (in orange) of a functionf (x,y) =e^xln(1 +y)around the origin.

In order to compute a second-order Taylor series expansion around point(a,b) = (0, 0)of the function $$f(x,y)=e^{x}\ln(1+y),$$

one first computes all the necessary partial derivatives:

$${\begin{aligned}f_{x}&=e^{x}\ln(1+y)\\[6pt]f_{y}&={\frac {e^{x}}{1+y}}\\[6pt]f_{xx}&=e^{x}\ln(1+y)\\[6pt]f_{yy}&=-{\frac {e^{x}}{(1+y)^{2}}}\\[6pt]f_{xy}&=f_{yx}={\frac {e^{x}}{1+y}}.\end{aligned}}$$

Evaluating these derivatives at the origin gives the Taylor coefficients

$${\begin{aligned}f_{x}(0,0)&=0\\f_{y}(0,0)&=1\\f_{xx}(0,0)&=0\\f_{yy}(0,0)&=-1\\f_{xy}(0,0)&=f_{yx}(0,0)=1.\end{aligned}}$$

Substituting these values in to the general formula

$${\begin{aligned}T(x,y)=&f(a,b)+(x-a)f_{x}(a,b)+(y-b)f_{y}(a,b)\\&{}+{\frac {1}{2!}}\left((x-a)^{2}f_{xx}(a,b)+2(x-a)(y-b)f_{xy}(a,b)+(y-b)^{2}f_{yy}(a,b)\right)+\cdots \end{aligned}}$$

produces

$${\begin{aligned}T(x,y)&=0+0(x-0)+1(y-0)+{\frac {1}{2}}{\big (}0(x-0)^{2}+2(x-0)(y-0)+(-1)(y-0)^{2}{\big )}+\cdots \\&=y+xy-{\tfrac {1}{2}}y^{2}+\cdots \end{aligned}}$$

Sinceln(1 +y)is analytic in|y| < 1,we have

$$e^{x}\ln(1+y)=y+xy-{\tfrac {1}{2}}y^{2}+\cdots,\qquad |y|<1.$$

Comparison with Fourier series

Main article:Fourier series

The trigonometricFourier seriesenables one to express aperiodic function(or a function defined on a closed interval[a,b]) as an infinite sum oftrigonometric functions(sinesandcosines). In this sense, the Fourier series is analogous to Taylor series, since the latter allows one to express a function as an infinite sum ofpowers.Nevertheless, the two series differ from each other in several relevant issues:

• The finite truncations of the Taylor series off (x)about the pointx=aare all exactly equal tofata.In contrast, the Fourier series is computed by integrating over an entire interval, so there is generally no such point where all the finite truncations of the series are exact.
• The computation of Taylor series requires the knowledge of the function on an arbitrary smallneighbourhoodof a point, whereas the computation of the Fourier series requires knowing the function on its whole domaininterval.In a certain sense one could say that the Taylor series is "local" and the Fourier series is "global".
• The Taylor series is defined for a function which has infinitely many derivatives at a single point, whereas the Fourier series is defined for anyintegrable function.In particular, the function could be nowhere differentiable. (For example,f (x)could be aWeierstrass function.)
• The convergence of both series has very different properties. Even if the Taylor series has positive convergence radius, the resulting series may not coincide with the function; but if the function is analytic then the series convergespointwiseto the function, anduniformlyon every compact subset of the convergence interval. Concerning the Fourier series, if the function issquare-integrablethen the series converges inquadratic mean,but additional requirements are needed to ensure the pointwise or uniform convergence (for instance, if the function is periodic and of class C¹then the convergence is uniform).
• Finally, in practice one wants to approximate the function with a finite number of terms, say with a Taylor polynomial or a partial sum of the trigonometric series, respectively. In the case of the Taylor series the error is very small in a neighbourhood of the point where it is computed, while it may be very large at a distant point. In the case of the Fourier series the error is distributed along the domain of the function.

See also

• Asymptotic expansion
• Newton polynomial
• Padé approximant– best approximation by a rational function
• Puiseux series– Power series with rational exponents
• Approximation theory
• Function approximation

References

• Abramowitz, Milton;Stegun, Irene A.(1970).Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables.New York:Dover Publications.Ninth printing.
• Banner, Adrian (2007).The Calculus Lifesaver: All the Tools You Need to Excel at Calculus.Princeton University Press.ISBN978-0-691-13088-0.
• Bilodeau, Gerald; Thie, Paul; Keough, G. E. (2010).An Introduction to Analysis.Jones & Bartlett Publisher.ISBN978-0-7637-7492-9.
• Boyer, C.;Merzbach, U.(1991).A History of Mathematics(2nd ed.). John Wiley and Sons.ISBN0-471-09763-2.
• Bruce, Ian (2007)."Methodus Incrementorum Directa & Inversa]".17centurymaths.
• Dani, S. G. (2012). "Ancient Indian Mathematics – A Conspectus".Resonance.17(3): 236–246.doi:10.1007/s12045-012-0022-y.S2CID120553186.
• Feigenbaum, L. (1985). "Brook Taylor and the method of increments".Archive for History of Exact Sciences.34(1–2): 1–140.doi:10.1007/bf00329903.S2CID122105736.
• Feller, William(2003) [1971].An introduction to probability theory and its applications.Vol. 2 (3rd ed.). Wiley.ISBN9789971512989.OCLC818811840.
• Greenberg, Michael (1998).Advanced Engineering Mathematics(2nd ed.). Prentice Hall.ISBN0-13-321431-1.
• Hille, Einar;Phillips, Ralph S.(1957).Functional analysis and semi-groups.AMS Colloquium Publications. Vol. 31. American Mathematical Society.
• Hofmann, Josef Ehrenfried (1939). "On the Discovery of the Logarithmic Series and Its Development in England up to Cotes".National Mathematics Magazine.14(1): 33–45.doi:10.2307/3028095.JSTOR3028095.
• Hörmander, Lars(2002) [1990]."1. Test Functions §1.1. A review of Differential Calculus".The analysis of partial differential operators.Vol. 1 (2nd ed.). Springer.doi:10.1007/978-3-642-61497-2_2.ISBN978-3-642-61497-2.
• Kline, M. (1990).Mathematical Thought from Ancient to Modern Times.New York: Oxford University Press.ISBN0-19-506135-7.
• Kolk, Johan A.C.; Duistermaat, J.J. (2010)."Taylor Expansion in Several Variables".Distributions: Theory and applications.Birkhauser.doi:10.1007/978-0-8176-4675-2_6.ISBN978-0-8176-4672-1.
• Lindberg, David (2007).The Beginnings of Western Science(2nd ed.). University of Chicago Press.ISBN978-0-226-48205-7.
• Malet, Antoni (1993). "James Gregorie on Tangents and the" Taylor "Rule for Series Expansions".Archive for History of Exact Sciences.46(2): 97–137.doi:10.1007/BF00375656.JSTOR41133959.S2CID120101519.
• Roy, Ranjan (1990)."The Discovery of the Series Formula forπby Leibniz, Gregory and Nilakantha "(PDF).Mathematics Magazine.63(5): 291–306.doi:10.1080/0025570X.1990.11977541.Archived fromthe original(PDF)on 2023-03-14.Retrieved2023-02-18.
• —— (2021) [2011].Series and Products in the Development of Mathematics.Vol. 1 (2nd ed.). Cambridge University Press.
• Rudin, Walter(1980).Real and Complex Analysis.New Delhi: McGraw-Hill.ISBN0-07-099557-5.
• Struik, D. J. (1969).A Source Book in Mathematics 1200–1800.Harvard University Press.ISBN978-0-674-82355-6.
• Taylor, Brook (1715).Methodus Incrementorum Directa et Inversa[Direct and Reverse Methods of Incrementation] (in Latin). London.
• Thomas, George B. Jr.; Finney, Ross L. (1996).Calculus and Analytic Geometry(9th ed.). Addison Wesley.ISBN0-201-53174-7.
• Turnbull, Herbert Westren, ed. (1939).James Gregory; Tercentenary Memorial Volume.G. Bell & Sons.

External links

• "Taylor series",Encyclopedia of Mathematics,EMS Press,2001 [1994]
• Weisstein, Eric W."Taylor Series".MathWorld.