Modular group

Inmathematics,themodular groupis theprojective special linear group ${\textstyle \operatorname {PSL} (2,\mathbb {Z} )}$ of2 × 2matriceswithintegercoefficients anddeterminant1. The matrices $A$ and $- A$ are identified. The modular group acts on the upper-half of thecomplex planebyfractional linear transformations,and the name "modular group" comes from the relation tomoduli spacesand not frommodular arithmetic.

Definition[edit]

Themodular group $Γ$ is thegroupoflinear fractional transformationsof theupper half of the complex plane,which have the form

z\mapsto {\frac {az+b}{cz+d}}

where $a$ , $b$ , $c$ , $d$ are integers, and $ad - bc = 1$ .The group operation isfunction composition.

This group of transformations is isomorphic to theprojective special linear group $PSL(2, Z)$ ,which is the quotient of the 2-dimensionalspecial linear group $SL(2, Z)$ over the integers by itscenter ${I,- I}$ .In other words, $PSL(2, Z)$ consists of all matrices

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}

where $a$ , $b$ , $c$ , $d$ are integers, $ad - bc = 1$ ,and pairs of matrices $A$ and $- A$ are considered to be identical. The group operation is the usualmultiplication of matrices.

Some authorsdefinethe modular group to be $PSL(2, Z)$ ,and still others define the modular group to be the larger group $SL(2, Z)$ .

Some mathematical relations require the consideration of the group $GL(2, Z)$ of matrices with determinant plus or minus one. ( $SL(2, Z)$ is a subgroup of this group.) Similarly, $PGL(2, Z)$ is the quotient group $GL(2, Z)/{I,- I}$ .A2 × 2matrix with unit determinant is asymplectic matrix,and thus $SL(2, Z) = Sp(2, Z)$ ,thesymplectic groupof2 × 2matrices.

Finding elements[edit]

To find an explicit matrix

${\begin{pmatrix}a&x\\b&y\end{pmatrix}}$

in $SL(2, Z)$ ,begin with two coprime integers $a,b$ ,and solve the determinant equation

$ay-bx=1.$

(Notice the determinant equation forces $a,b$ to be coprime since otherwise there would be a factor $c>1$ such that $ca'=a$ , $cb'=b$ ,hence

$c(a'y-b'x)=1$

would have no integer solutions.) For example, if $a=7,{\text{ }}b=6$ then the determinant equation reads

$7y-6x=1$

then taking $y=-5$ and $x=-6$ gives $-35-(-36)=1$ ,hence

${\begin{pmatrix}7&-6\\6&-5\end{pmatrix}}$

is a matrix. Then, using the projection, these matrices define elements in $PSL(2, Z)$ .

Number-theoretic properties[edit]

The unit determinant of

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}

implies that the fractions_{$.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠a/b⁠$},_{$⁠ a / c ⁠$},_{$⁠ c / d ⁠$},_{$⁠ b / d ⁠$}are all irreducible, that is having no common factors (provided the denominators are non-zero, of course). More generally, if $⁠ p / q ⁠$ is an irreducible fraction, then

{\frac {ap+bq}{cp+dq}}

is also irreducible (again, provided the denominator be non-zero). Any pair of irreducible fractions can be connected in this way; that is, for any pair $⁠ p / q ⁠$ and $⁠ r / s ⁠$ of irreducible fractions, there exist elements

{\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \operatorname {SL} (2,\mathbb {Z} )

such that

r=ap+bq\quad {\mbox{ and }}\quad s=cp+dq.

Elements of the modular group provide a symmetry on the two-dimensionallattice.Let $ω 1$ and $ω 2$ be twocomplex numberswhose ratio is not real. Then the set of points

\Lambda (\ Omega _{1},\ Omega _{2})=\{m\ Omega _{1}+n\ Omega _{2}:m,n\in \mathbb {Z} \}

is a lattice of parallelograms on the plane. A different pair of vectors $α 1$ and $α 2$ will generate exactly the same lattice if and only if

{\begin{pmatrix}\ Alpha _{1}\\\ Alpha _{2}\end{pmatrix}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}\ Omega _{1}\\\ Omega _{2}\end{pmatrix}}

for some matrix in $GL(2, Z)$ .It is for this reason thatdoubly periodic functions,such aselliptic functions,possess a modular group symmetry.

The action of the modular group on the rational numbers can most easily be understood by envisioning a square grid, with grid point $(p, q)$ corresponding to the fraction $⁠ p / q ⁠$ (seeEuclid's orchard). An irreducible fraction is one that isvisiblefrom the origin; the action of the modular group on a fraction never takes avisible(irreducible) to ahidden(reducible) one, and vice versa.

Note that any member of the modular group maps theprojectively extended real lineone-to-one to itself, and furthermore bijectively maps the projectively extended rational line (the rationals with infinity) to itself, theirrationalsto the irrationals, thetranscendental numbersto the transcendental numbers, the non-real numbers to the non-real numbers, the upper half-plane to the upper half-plane, et cetera.

If $⁠ p n -1 / q n -1 ⁠$ and $⁠ p n / q n ⁠$ are two successive convergents of acontinued fraction,then the matrix

{\begin{pmatrix}p_{n-1}&p_{n}\\q_{n-1}&q_{n}\end{pmatrix}}

belongs to $GL(2, Z)$ .In particular, if $bc - ad = 1$ for positive integers $a$ , $b$ , $c$ , $d$ with $a < b$ and $c < d$ then $⁠ a / b ⁠$ and $⁠ c / d ⁠$ will be neighbours in theFarey sequenceof order $max(b, d)$ .Important special cases of continued fraction convergents include theFibonacci numbersand solutions toPell's equation.In both cases, the numbers can be arranged to form asemigroupsubset of the modular group.

Group-theoretic properties[edit]

Presentation[edit]

The modular group can be shown to begeneratedby the two transformations

{\begin{aligned}S&:z\mapsto -{\frac {1}{z}}\\T&:z\mapsto z+1\end{aligned}}

so that every element in the modular group can be represented (in a non-unique way) by the composition of powers of $S$ and $T$ .Geometrically, $S$ represents inversion in the unit circle followed by reflection with respect to the imaginary axis, while $T$ represents a unit translation to the right.

The generators $S$ and $T$ obey the relations $S 2 = 1$ and $(ST) 3 = 1$ .It can be shown^[1]that these are a complete set of relations, so the modular group has thepresentation:

\Gamma \cong \left\langle S,T\mid S^{2}=I,\left(ST\right)^{3}=I\right\rangle

This presentation describes the modular group as the rotationaltriangle group $D(2, 3, \infty)$ (infinity as there is no relation on $T$ ), and it thus maps onto all triangle groups $(2, 3, n)$ by adding the relation $T n = 1$ ,which occurs for instance in thecongruence subgroup $Γ(n)$ .

Using the generators $S$ and $ST$ instead of $S$ and $T$ ,this shows that the modular group is isomorphic to thefree productof thecyclic groups $C 2$ and $C 3$ :

\Gamma \cong C_{2}*C_{3}

The action of $T : z \mapsto z + 1$ on $H$
The action of $S : z \mapsto - ⁠ 1 / z ⁠$ on $H$

Braid group[edit]

Thebraid group $B 3$ is the universal central extension of the modular group, with these sitting as lattices inside the (topological) universal covering group $SL 2 (R) \to PSL 2 (R)$ .Further, the modular group has a trivial center, and thus the modular group is isomorphic to thequotient groupof $B 3$ modulo itscenter;equivalently, to the group ofinner automorphismsof $B 3$ .

The braid group $B 3$ in turn is isomorphic to theknot groupof thetrefoil knot.

Quotients[edit]

The quotients by congruence subgroups are of significant interest.

Other important quotients are the $(2, 3, n)$ triangle groups, which correspond geometrically to descending to a cylinder, quotienting the $x$ coordinatemodulo $n$ ,as $T n = (z \mapsto z + n)$ . $(2, 3, 5)$ is the group oficosahedral symmetry,and the $(2, 3, 7)$ triangle group(and associated tiling) is the cover for allHurwitz surfaces.

Presenting as a matrix group[edit]

The group ${\text{SL}}_{2}(\mathbb {Z} )$ can be generated by the two matrices^[2]

S={\begin{pmatrix}0&-1\\1&0\end{pmatrix}},{\text{ }}T={\begin{pmatrix}1&1\\0&1\end{pmatrix}}

since

S^{2}=-I_{2},{\text{ }}(ST)^{3}={\begin{pmatrix}0&-1\\1&1\end{pmatrix}}^{3}=-I_{2}

The projection ${\text{SL}}_{2}(\mathbb {Z} )\to {\text{PSL}}_{2}(\mathbb {Z} )$ turns these matrices into generators of ${\text{PSL}}_{2}(\mathbb {Z} )$ ,with relations similar to the group presentation.

Relationship to hyperbolic geometry[edit]

The modular group is important because it forms asubgroupof the group ofisometriesof thehyperbolic plane.If we consider theupper half-planemodel $H$ of hyperbolic plane geometry, then the group of all orientation-preservingisometries of $H$ consists of allMöbius transformationsof the form

z\mapsto {\frac {az+b}{cz+d}}

where $a$ , $b$ , $c$ , $d$ arereal numbers.In terms ofprojective coordinates,the group $PSL(2, R)$ actson the upper half-plane $H$ by projectivity:

[z,\ 1]{\begin{pmatrix}a&c\\b&d\end{pmatrix}}\,=\,[az+b,\ cz+d]\,\thicksim \,\left[{\frac {az+b}{cz+d}},\ 1\right].

This action isfaithful.Since $PSL(2, Z)$ is a subgroup of $PSL(2, R)$ ,the modular group is a subgroup of the group of orientation-preserving isometries of $H$ .^[3]

Tessellation of the hyperbolic plane[edit]

A typical fundamental domain for the action of $Γ$ on the upper half-plane.

The modular group $Γ$ acts on ${\textstyle \mathbb {H} }$ as adiscrete subgroupof ${\textstyle \operatorname {PSL} (2,\mathbb {R} )}$ ,that is, for each $z$ in ${\textstyle \mathbb {H} }$ we can find a neighbourhood of $z$ which does not contain any other element of theorbitof $z$ .This also means that we can constructfundamental domains,which (roughly) contain exactly one representative from the orbit of every $z$ in $H$ .(Care is needed on the boundary of the domain.)

There are many ways of constructing a fundamental domain, but a common choice is the region

R=\left\{z\in \mathbb {H} \colon \left|z\right|>1,\,\left|\operatorname {Re} (z)\right|<{\tfrac {1}{2}}\right\}

bounded by the vertical lines $Re(z) = ⁠ 1 / 2 ⁠$ and $Re(z) = - ⁠ 1 / 2 ⁠$ ,and the circle $| z | = 1$ .This region is a hyperbolic triangle. It has vertices at $⁠ 1 / 2 ⁠ + i ⁠ \sqrt 3 / 2 ⁠$ and $- ⁠ 1 / 2 ⁠ + i ⁠ \sqrt 3 / 2 ⁠$ ,where the angle between its sides is $⁠ π / 3 ⁠$ ,and a third vertex at infinity, where the angle between its sides is 0.

There is a strong connection between the modular group andelliptic curves.Each point $z$ in the upper half-plane gives an elliptic curve, namely the quotient of $\mathbb {C}$ by the lattice generated by 1 and $z$ . Two points in the upper half-plane give isomorphic elliptic curves if and only if they are related by a transformation in the modular group. Thus, the quotient of the upper half-plane by the action of the modular group is the so-calledmoduli spaceof elliptic curves: a space whose points describe isomorphism classes of elliptic curves. This is often visualized as the fundamental domain described above, with some points on its boundary identified.

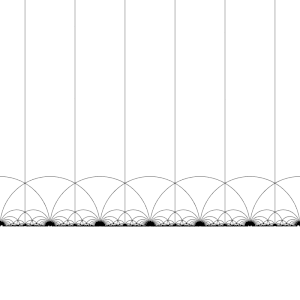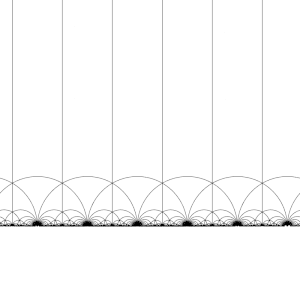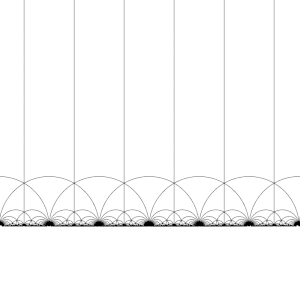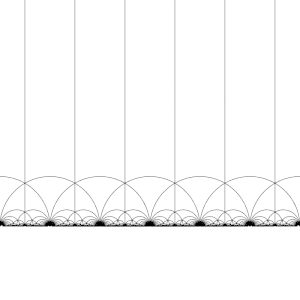
The modular group and its subgroups are also a source of interesting tilings of the hyperbolic plane. By transforming this fundamental domain in turn by each of the elements of the modular group, aregular tessellationof the hyperbolic plane by congruent hyperbolic triangles known as the V6.6.∞Infinite-order triangular tilingis created. Note that each such triangle has one vertex either at infinity or on the real axis $Im(z) = 0$ .

This tiling can be extended to thePoincaré disk,where every hyperbolic triangle has one vertex on the boundary of the disk. The tiling of the Poincaré disk is given in a natural way by the $J$ -invariant,which is invariant under the modular group, and attains every complex number once in each triangle of these regions.

This tessellation can be refined slightly, dividing each region into two halves (conventionally colored black and white), by adding an orientation-reversing map; the colors then correspond to orientation of the domain. Adding in $(x, y) \mapsto (- x, y)$ and taking the right half of the region $R$ (where $Re(z) \geq 0$ ) yields the usual tessellation. This tessellation first appears in print in (Klein & 1878/79a),^[4]where it is credited toRichard Dedekind,in reference to (Dedekind 1877).^[4]^[5]

The map of groups $(2, 3, \infty) \to (2, 3, n)$ (from modular group to triangle group) can be visualized in terms of this tiling (yielding a tiling on the modular curve), as depicted in the video at right.

Paracompact uniform tilings in [∞,3] family v t e
Symmetry:[∞,3], (*∞32)							[∞,3]⁺ (∞32)	[1⁺,∞,3] (*∞33)		[∞,3⁺] (3*∞)

		=	=	=				= or	= or	=

{∞,3}	t{∞,3}	r{∞,3}	t{3,∞}	{3,∞}	rr{∞,3}	tr{∞,3}	sr{∞,3}	h{∞,3}	h₂{∞,3}	s{3,∞}
Uniform duals


V∞³	V3.∞.∞	V(3.∞)²	V6.6.∞	V3^∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V(3.∞)³		V3.3.3.3.3.∞

Congruence subgroups[edit]

Importantsubgroupsof the modular group $Γ$ ,calledcongruence subgroups,are given by imposingcongruence relationson the associated matrices.

There is a naturalhomomorphism $SL(2, Z) \to SL(2, Z / N Z)$ given by reducing the entriesmodulo $N$ .This induces a homomorphism on the modular group $PSL(2, Z) \to PSL(2, Z / N Z)$ .Thekernelof this homomorphism is called theprincipal congruence subgroupof level $N$ ,denoted $Γ(N)$ .We have the followingshort exact sequence:

1\to \Gamma (N)\to \Gamma \to \operatorname {PSL} (2,\mathbb {Z} /N\mathbb {Z} )\to 1.

Being the kernel of a homomorphism $Γ(N)$ is anormal subgroupof the modular group $Γ$ .The group $Γ(N)$ is given as the set of all modular transformations

z\mapsto {\frac {az+b}{cz+d}}

for which $a \equiv d \equiv \pm1 (mod N)$ and $b \equiv c \equiv 0 (mod N)$ .

It is easy to show that thetraceof a matrix representing an element of $Γ(N)$ cannot be −1, 0, or 1, so these subgroups aretorsion-free groups.(There are other torsion-free subgroups.)

The principal congruence subgroup of level 2, $Γ(2)$ ,is also called themodular group $Λ$ .Since $PSL(2, Z /2 Z)$ is isomorphic to $S 3$ , $Λ$ is a subgroup ofindex6. The group $Λ$ consists of all modular transformations for which $a$ and $d$ are odd and $b$ and $c$ are even.

Another important family of congruence subgroups are themodular group $Γ 0 (N)$ defined as the set of all modular transformations for which $c \equiv 0 (mod N)$ ,or equivalently, as the subgroup whose matrices becomeupper triangularupon reduction modulo $N$ .Note that $Γ(N)$ is a subgroup of $Γ 0 (N)$ .Themodular curvesassociated with these groups are an aspect ofmonstrous moonshine– for aprime number $p$ ,the modular curve of the normalizer isgenuszero if and only if $p$ divides theorderof themonster group,or equivalently, if $p$ is asupersingular prime.

Dyadic monoid[edit]

One important subset of the modular group is thedyadic monoid,which is themonoidof all strings of the form $ST k ST m ST n ...$ for positive integers $k, m, n,...$ .This monoid occurs naturally in the study offractal curves,and describes theself-similaritysymmetries of theCantor function,Minkowski's question mark function,and theKoch snowflake,each being a special case of the generalde Rham curve.The monoid also has higher-dimensional linear representations; for example, the $N = 3$ representation can be understood to describe the self-symmetry of theblancmange curve.

Maps of the torus[edit]

The group $GL(2, Z)$ is the linear maps preserving the standard lattice $Z 2$ ,and $SL(2, Z)$ is the orientation-preserving maps preserving this lattice; they thus descend toself-homeomorphismsof thetorus(SL mapping to orientation-preserving maps), and in fact map isomorphically to the (extended)mapping class groupof the torus, meaning that every self-homeomorphism of the torus isisotopicto a map of this form. The algebraic properties of a matrix as an element of $GL(2, Z)$ correspond to the dynamics of the induced map of the torus.

Hecke groups[edit]

The modular group can be generalized to theHecke groups,named forErich Hecke,and defined as follows.^[7]

The Hecke group $H q$ with $q \geq 3$ ,is the discrete group generated by

{\begin{aligned}z&\mapsto -{\frac {1}{z}}\\z&\mapsto z+\lambda _{q},\end{aligned}}

where $λ q = 2 cos ⁠ π / q ⁠$ .For small values of $q \geq 3$ ,one has:

{\begin{aligned}\lambda _{3}&=1,\\\lambda _{4}&={\sqrt {2}},\\\lambda _{5}&={\frac {1+{\sqrt {5}}}{2}},\\\lambda _{6}&={\sqrt {3}},\\\lambda _{8}&={\sqrt {2+{\sqrt {2}}}}.\end{aligned}}

The modular group $Γ$ is isomorphic to $H 3$ and they share properties and applications – for example, just as one has thefree productofcyclic groups

\Gamma \cong C_{2}*C_{3},

more generally one has

H_{q}\cong C_{2}*C_{q},

which corresponds to thetriangle group $(2, q,\infty)$ .There is similarly a notion of principal congruence subgroups associated to principal ideals in $Z [λ]$ .

History[edit]

The modular group and its subgroups were first studied in detail byRichard Dedekindand byFelix Kleinas part of hisErlangen programmein the 1870s. However, the closely relatedelliptic functionswere studied byJoseph Louis Lagrangein 1785, and further results on elliptic functions were published byCarl Gustav Jakob JacobiandNiels Henrik Abelin 1827.

References[edit]

^Alperin, Roger C.(April 1993). " $PSL 2 (Z) = Z 2 * Z 3$ ".Amer. Math. Monthly.100(4): 385–386.doi:10.2307/2324963.JSTOR 2324963.
^Conrad, Keith."SL(2,Z)"(PDF).
^McCreary, Paul R.; Murphy, Teri Jo; Carter, Christian."The Modular Group"(PDF).The Mathematica Journal.9(3).
^^a ^bLe Bruyn, Lieven (22 April 2008),Dedekind or Klein?
^Stillwell, John (January 2001). "Modular Miracles".The American Mathematical Monthly.108(1): 70–76.doi:10.2307/2695682.ISSN 0002-9890.JSTOR 2695682.
^Westendorp, Gerard."Platonic tessellations of Riemann surfaces".xs4all.nl.
^Rosenberger, Gerhard; Fine, Benjamin; Gaglione, Anthony M.; Spellman, Dennis (2006).Combinatorial Group Theory, Discrete Groups, and Number Theory.p. 65.ISBN 9780821839850.

Apostol, Tom M. (1990).Modular Functions and Dirichlet Series in Number Theory(2nd ed.). New York: Springer. ch. 2.ISBN 0-387-97127-0.
Klein, Felix(1878–1879),"Über die Transformation der elliptischen Funktionen und die Auflösung der Gleichungen fünften Grades (On the transformation of elliptic functions and...)",Math. Annalen,14:13–75,doi:10.1007/BF02297507,S2CID 121056952,archived fromthe originalon 19 July 2011,retrieved3 June2010
Dedekind, Richard(September 1877), "Schreiben an Herrn Borchardt über die Theorie der elliptische Modul-Functionen",Crelle's Journal,83:265–292.

[1] Alperin, Roger C.(April 1993). " $PSL 2 (Z) = Z 2 * Z 3$ ".Amer. Math. Monthly.100(4): 385–386.doi:10.2307/2324963.JSTOR 2324963.

[2] Conrad, Keith."SL(2,Z)"(PDF).

[3] McCreary, Paul R.; Murphy, Teri Jo; Carter, Christian."The Modular Group"(PDF).The Mathematica Journal.9(3).

[lebruyn-4] Le Bruyn, Lieven (22 April 2008),Dedekind or Klein?

[5] Stillwell, John (January 2001). "Modular Miracles".The American Mathematical Monthly.108(1): 70–76.doi:10.2307/2695682.ISSN 0002-9890.JSTOR 2695682.

[westendorp-6] Westendorp, Gerard."Platonic tessellations of Riemann surfaces".xs4all.nl.

[7] Rosenberger, Gerhard; Fine, Benjamin; Gaglione, Anthony M.; Spellman, Dennis (2006).Combinatorial Group Theory, Discrete Groups, and Number Theory.p. 65.ISBN 9780821839850.

[1]

[2]

[3]

[4]

[5]

[6]

[7]