Multidimensional sampling

Indigital signal processing,multidimensional samplingis the process of converting a function of a multidimensional variable into a discrete collection of values of the function measured on a discrete set of points. This article presents the basic result due to Petersen and Middletonon conditions for perfectly reconstructing awavenumber-limited function from its measurements on a discretelatticeof points. This result, also known as thePetersen–Middleton theorem,is a generalization of theNyquist–Shannon sampling theoremfor sampling one-dimensionalband-limitedfunctions to higher-dimensionalEuclidean spaces.

In essence, the Petersen–Middleton theorem shows that a wavenumber-limited function can be perfectly reconstructed from its values on an infinite lattice of points, provided the lattice is fine enough. The theorem provides conditions on the lattice under which perfect reconstruction is possible.

As with the Nyquist–Shannon sampling theorem, this theorem also assumes an idealization of any real-world situation, as it only applies to functions that are sampled over an infinitude of points. Perfect reconstruction is mathematically possible for the idealized model but only an approximation for real-world functions and sampling techniques, albeit in practice often a very good one.

Preliminaries

Fig. 1: A hexagonal sampling lattice$\Lambda$and its basis vectorsv₁andv₂

Fig. 2: The reciprocal lattice$\Gamma$corresponding to the lattice$\Lambda$of Fig. 1 and its basis vectorsu₁andu₂(figure not to scale).

The concept of abandlimitedfunction in one dimension can be generalized to the notion of a wavenumber-limited function in higher dimensions. Recall that theFourier transformof an integrable function$f(\cdot )$onn-dimensional Euclidean space is defined as:

${\hat {f}}(\xi )={\mathcal {F}}(f)(\xi )=\int _{\Re ^{n}}f(x)e^{-2\pi i\langle x,\xi \rangle }\,dx$

wherexandξaren-dimensionalvectors,and$\langle x,\xi \rangle$is theinner productof the vectors. The function$f(\cdot )$is said to be wavenumber-limited to a set$\Omega$if the Fourier transform satisfies${\hat {f}}(\xi )=0$for$\xi \notin \Omega$.

Similarly, the configuration of uniformly spaced sampling points in one-dimension can be generalized to alatticein higher dimensions. A lattice is a collection of points$\Lambda \subset \Re ^{n}$of the form $\Lambda =\left\{\sum _{i=1}^{n}a_{i}v_{i}\;|\;a_{i}\in \mathbb {Z} \right\}$ where {v₁,...,v_n} is abasisfor$\Re ^{n}$.Thereciprocal lattice$\Gamma$corresponding to$\Lambda$is defined by

$\Gamma =\left\{\sum _{i=1}^{n}a_{i}u_{i}\;|\;a_{i}\in \mathbb {Z} \right\}$

where the vectors$u_{i}$are chosen to satisfy$\langle u_{i},v_{j}\rangle =\delta _{ij}$.That is, if the vectors$u_{i}$form columns of a matrix$A$and$v_{i}$the columns of a matrix$B$,then$A=B^{-T}$.An example of a sampling lattice in two dimensional space is ahexagonal latticedepicted in Figure 1. The corresponding reciprocal lattice is shown in Figure 2. The reciprocal lattice of asquare latticein two dimensions is another square lattice. In three dimensional space the reciprocal lattice of a face-centered cubic (FCC) latticeis a body centered cubic (BCC) lattice.

The theorem

Let$\Lambda$denote a lattice in$\Re ^{n}$and$\Gamma$the corresponding reciprocal lattice. The theorem of Petersen and Middletonstates that a function$f(\cdot )$that is wavenumber-limited to a set$\Omega \subset \Re ^{n}$can be exactly reconstructed from its measurements on$\Lambda$provided that the set$\Omega$does not overlap with any of its shifted versions$\Omega +x$where the shiftxis any nonzero element of the reciprocal lattice$\Gamma$.In other words,$f(\cdot )$can be exactly reconstructed from its measurements on$\Lambda$provided that$\Omega \cap \{x+y:y\in \Omega \}=\emptyset$for all$x\in \Gamma \setminus \{0\}$.

Reconstruction

Fig. 3: Support of the sampled spectrum${\hat {f}}_{s}(\cdot )$obtained by hexagonal sampling of a two-dimensional function wavenumber-limited to a circular disc. The blue circle represents the support$\Omega$of the original wavenumber-limited field, and the green circles represent the repetitions. In this example the spectral repetitions do not overlap and hence there is no aliasing. The original spectrum can be exactly recovered from the sampled spectrum.

The generalization of thePoisson summation formulato higher dimensionscan be used to show that the samples,$\{f(x):x\in \Lambda \}$,of the function$f(\cdot )$on the lattice$\Lambda$are sufficient to create aperiodic summationof the function${\hat {f}}(\cdot )$.The result is:

${\hat {f}}_{s}(\xi )\ {\stackrel {\mathrm {def} }{=}}\sum _{y\in \Gamma }{\hat {f}}\left(\xi -y\right)=\sum _{x\in \Lambda }|\Lambda |f(x)\ e^{-i2\pi \langle x,\xi \rangle },$(Eq.1)

where$|\Lambda |$represents the volume of theparallelepipedformed by the vectors {v₁,...,v_n}. This periodic function is often referred to as the sampled spectrum and can be interpreted as the analogue of thediscrete-time Fourier transform(DTFT) in higher dimensions. If the original wavenumber-limited spectrum${\hat {f}}(\cdot )$is supported on the set$\Omega$then the function${\hat {f}}_{s}(\cdot )$is supported on periodic repetitions of$\Omega$shifted by points on the reciprocal lattice$\Gamma$.If the conditions of the Petersen-Middleton theorem are met, then the function${\hat {f}}_{s}(\xi )$is equal to${\hat {f}}(\xi )$for all$\xi \in \Omega$,and hence the original field can be exactly reconstructed from the samples. In this case the reconstructed field matches the original field and can be expressed in terms of the samples as

$f(x)=\sum _{y\in \Lambda }|\Lambda |f(y){\check {\chi }}_{\Omega }(y-x)$,(Eq.2)

where${\check {\chi }}_{\Omega }(\cdot )$is the inverse Fourier transform of thecharacteristic functionof the set$\Omega$.This interpolation formula is the higher-dimensional equivalent of theWhittaker–Shannon interpolation formula.

As an example suppose that$\Omega$is a circular disc. Figure 3 illustrates the support of${\hat {f}}_{s}(\cdot )$when the conditions of the Petersen-Middleton theorem are met. We see that the spectral repetitions do not overlap and hence the original spectrum can be exactly recovered.

Implications

Aliasing

Main article:Aliasing

Fig. 4: Support of the sampled spectrum${\hat {f}}_{s}(\cdot )$obtained by hexagonal sampling of a two-dimensional function wavenumber-limited to a circular disc. In this example, the sampling lattice is not fine enough and hence the discs overlap in the sampled spectrum. Thus the spectrum within$\Omega$represented by the blue circle cannot be recovered exactly due to the overlap from the repetitions (shown in green), thus leading to aliasing.

Fig. 5: Spatial aliasing in the form of aMoiré pattern.

Fig. 6: Properly sampled image of brick wall.

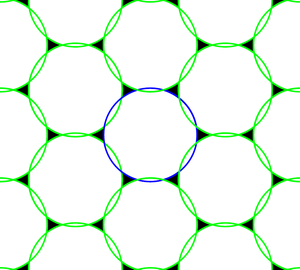
The theorem gives conditions on sampling lattices for perfect reconstruction of the sampled. If the lattices are not fine enough to satisfy the Petersen-Middleton condition, then the field cannot be reconstructed exactly from the samples in general. In this case we say that the samples may bealiased.Again, consider the example in which$\Omega$is a circular disc. If the Petersen-Middleton conditions do not hold, the support of the sampled spectrum will be as shown in Figure 4. In this case the spectral repetitions overlap leading to aliasing in the reconstruction.

A simple illustration of aliasing can be obtained by studying low-resolution images. A gray-scale image can be interpreted as a function in two-dimensional space. An example of aliasing is shown in the images of brick patterns in Figure 5. The image shows the effects of aliasing when the sampling theorem's condition is not satisfied. If the lattice of pixels is not fine enough for the scene, aliasing occurs as evidenced by the appearance of theMoiré patternin the image obtained. The image in Figure 6 is obtained when a smoothened version of the scene is sampled with the same lattice. In this case the conditions of the theorem are satisfied and no aliasing occurs.

Optimal sampling lattices

One of the objects of interest in designing a sampling scheme for wavenumber-limited fields is to identify the configuration of points that leads to the minimum sampling density, i.e., the density of sampling points per unit spatial volume in$\Re ^{n}$.Typically the cost for taking and storing the measurements is proportional to the sampling density employed. Often in practice, the natural approach to sample two-dimensional fields is to sample it at points on arectangular lattice.However, this is not always the ideal choice in terms of the sampling density. The theorem of Petersen and Middleton can be used to identify the optimal lattice for sampling fields that are wavenumber-limited to a given set$\Omega \subset \Re ^{d}$.For example, it can be shown that the lattice in$\Re ^{2}$with minimum spatial density of points that admits perfect reconstructions of fields wavenumber-limited to a circular disc in$\Re ^{2}$is the hexagonal lattice.As a consequence, hexagonal lattices are preferred for samplingisotropic fieldsin$\Re ^{2}$.

Optimal sampling lattices have been studied in higher dimensions.Generally, optimalsphere packinglattices are ideal for sampling smooth stochastic processes while optimal sphere covering latticesare ideal for sampling rough stochastic processes.

Since optimal lattices, in general, are non-separable, designinginterpolationandreconstruction filtersrequires non-tensor-product (i.e., non-separable) filter design mechanisms.Box splinesprovide a flexible framework for designing such non-separable reconstructionFIRfilters that can be geometrically tailored for each lattice.Hex-splinesare the generalization ofB-splinesfor 2-D hexagonal lattices. Similarly, in 3-D and higher dimensions, Voronoi splinesprovide a generalization ofB-splinesthat can be used to design non-separable FIR filters which are geometrically tailored for any lattice, including optimal lattices.

Explicit construction of ideal low-pass filters (i.e.,sincfunctions) generalized to optimal lattices is possible by studying the geometric properties ofBrillouin zones(i.e.,$\Omega$in above) of these lattices (which arezonotopes).This approach provides a closed-form explicit representation of${\check {\chi }}_{\Omega }(\cdot )$for general lattices, including optimal sampling lattices. This construction provides a generalization of theLanczos filterin 1-D to the multidimensional setting for optimal lattices.

Applications

The Petersen–Middleton theorem is useful in designing efficient sensor placement strategies in applications involving measurement of spatial phenomena such as seismic surveys, environment monitoring and spatial audio-field measurements.