NP-completeness
This articlemay beconfusing or unclearto readers.(July 2012) |

Incomputational complexity theory,a problem isNP-completewhen:
- It is adecision problem,meaning that for any input to the problem, the output is either "yes" or "no".
- When the answer is "yes", this can be demonstrated through the existence of a short (polynomial length)solution.
- The correctness of each solution can be verified quickly (namely, inpolynomial time) and abrute-force searchalgorithm can find a solution by trying all possible solutions.
- The problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. In this sense, NP-complete problems are the hardest of the problems to which solutions can be verified quickly. If we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified.
The name "NP-complete" is short for "nondeterministic polynomial-time complete". In this name, "nondeterministic" refers tonondeterministic Turing machines,a way of mathematically formalizing the idea of a brute-force search algorithm.Polynomial timerefers to an amount of time that is considered "quick" for adeterministic algorithmto check a single solution, or for a nondeterministic Turing machine to perform the whole search. "Complete"refers to the property of being able to simulate everything in the samecomplexity class.
More precisely, each input to the problem should be associated with a set of solutions of polynomial length, the validity of each of which can be tested quickly (inpolynomial time),[2]such that the output for any input is "yes" if the solution set is non-empty and "no" if it is empty. The complexity class of problems of this form is calledNP,an abbreviation for "nondeterministic polynomial time". A problem is said to beNP-hardif everything in NP can be transformed in polynomial time into it even though it may not be in NP. A problem is NP-complete if it is both in NP and NP-hard. The NP-complete problems represent the hardest problems in NP. If some NP-complete problem has a polynomial time algorithm, all problems in NP do. The set of NP-complete problems is often denoted byNP-CorNPC.
Although a solution to an NP-complete problem can beverified"quickly", there is no known way tofinda solution quickly. That is, the time required to solve the problem using any currently knownalgorithmincreases rapidly as the size of the problem grows. As a consequence, determining whether it is possible to solve these problems quickly, called theP versus NP problem,is one of the fundamentalunsolved problems in computer sciencetoday.
While a method for computing the solutions to NP-complete problems quickly remains undiscovered,computer scientistsandprogrammersstill frequently encounter NP-complete problems. NP-complete problems are often addressed by usingheuristicmethods andapproximation algorithms.
Overview
[edit]NP-complete problems are inNP,the set of alldecision problemswhose solutions can be verified in polynomial time;NPmay be equivalently defined as the set of decision problems that can be solved in polynomial time on anon-deterministic Turing machine.A problempin NP is NP-complete if every other problem in NP can be transformed (or reduced) intopin polynomial time.[citation needed]
It is not known whether every problem in NP can be quickly solved—this is called theP versus NP problem.But ifany NP-complete problemcan be solved quickly, thenevery problem in NPcan, because the definition of an NP-complete problem states that every problem in NP must be quickly reducible to every NP-complete problem (that is, it can be reduced in polynomial time). Because of this, it is often said that NP-complete problems areharderormore difficultthan NP problems in general.[citation needed]
Formal definition
[edit]A decision problemis NP-complete if:[citation needed]
can be shown to be in NP by demonstrating that a candidate solution tocan be verified in polynomial time.
Note that a problem satisfying condition 2 is said to beNP-hard,whether or not it satisfies condition 1.[4]
A consequence of this definition is that if we had a polynomial time algorithm (on aUTM,or any otherTuring-equivalentabstract machine) for,we could solve all problems in NP in polynomial time.
Background
[edit]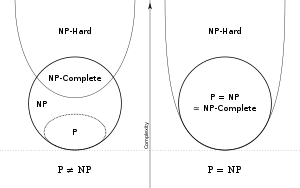
The concept of NP-completeness was introduced in 1971 (seeCook–Levin theorem), though the termNP-completewas introduced later. At the 1971STOCconference, there was a fierce debate between the computer scientists about whether NP-complete problems could be solved in polynomial time on adeterministicTuring machine.John Hopcroftbrought everyone at the conference to a consensus that the question of whether NP-complete problems are solvable in polynomial time should be put off to be solved at some later date, since nobody had any formal proofs for their claims one way or the other.[citation needed]This is known as "the question of whether P=NP".
Nobody has yet been able to determine conclusively whether NP-complete problems are in fact solvable in polynomial time, making this one of the greatunsolved problems of mathematics.TheClay Mathematics Instituteis offering a US$1 million reward (Millennium Prize) to anyone who has a formal proof that P=NP or that P≠NP.[5]
The existence of NP-complete problems is not obvious. TheCook–Levin theoremstates that theBoolean satisfiability problemis NP-complete, thus establishing that such problems do exist. In 1972,Richard Karpproved that several other problems were also NP-complete (seeKarp's 21 NP-complete problems); thus, there is a class of NP-complete problems (besides the Boolean satisfiability problem). Since the original results, thousands of other problems have been shown to be NP-complete by reductions from other problems previously shown to be NP-complete; many of these problems are collected inGarey & Johnson (1979).
NP-complete problems
[edit]
The easiest way to prove that some new problem is NP-complete is first to prove that it is in NP, and then to reduce some known NP-complete problem to it. Therefore, it is useful to know a variety of NP-complete problems. The list below contains some well-known problems that are NP-complete when expressed as decision problems.
To the right is a diagram of some of the problems and thereductionstypically used to prove their NP-completeness. In this diagram, problems are reduced from bottom to top. Note that this diagram is misleading as a description of the mathematical relationship between these problems, as there exists apolynomial-time reductionbetween any two NP-complete problems; but it indicates where demonstrating this polynomial-time reduction has been easiest.
There is often only a small difference between a problem in P and an NP-complete problem. For example, the3-satisfiabilityproblem, a restriction of the Boolean satisfiability problem, remains NP-complete, whereas the slightly more restricted2-satisfiabilityproblem is in P (specifically, it isNL-complete), but the slightly more general max. 2-sat. problem is again NP-complete. Determining whether a graph can be colored with 2 colors is in P, but with 3 colors is NP-complete, even when restricted toplanar graphs.Determining if a graph is acycleor isbipartiteis very easy (inL), but finding a maximum bipartite or a maximum cycle subgraph is NP-complete. A solution of theknapsack problemwithin any fixed percentage of the optimal solution can be computed in polynomial time, but finding the optimal solution is NP-complete.
Intermediate problems
[edit]An interesting example is thegraph isomorphism problem,thegraph theoryproblem of determining whether agraph isomorphismexists between two graphs. Two graphs areisomorphicif one can betransformedinto the other simply by renamingvertices.Consider these two problems:
- Graph Isomorphism: Is graph G1isomorphic to graph G2?
- Subgraph Isomorphism: Is graph G1isomorphic to a subgraph of graph G2?
The Subgraph Isomorphism problem is NP-complete. The graph isomorphism problem is suspected to be neither in P nor NP-complete, though it is in NP. This is an example of a problem that is thought to behard,but is not thought to be NP-complete. This class is calledNP-Intermediate problemsand exists if and only if P≠NP.
Solving NP-complete problems
[edit]At present, all known algorithms for NP-complete problems require time that issuperpolynomialin the input size. Thevertex coverproblem has[6]for someand it is unknown whether there are any faster algorithms.
The following techniques can be applied to solve computational problems in general, and they often give rise to substantially faster algorithms:
- Approximation:Instead of searching for an optimal solution, search for a solution that is at most a factor from an optimal one.
- Randomization:Use randomness to get a faster averagerunning time,and allow the algorithm to fail with some small probability. Note: TheMonte Carlo methodis not an example of an efficient algorithm in this specific sense, although evolutionary approaches likeGenetic algorithmsmay be.
- Restriction: By restricting the structure of the input (e.g., to planar graphs), faster algorithms are usually possible.
- Parameterization:Often there are fast algorithms if certain parameters of the input are fixed.
- Heuristic:An algorithm that works "reasonably well" in many cases, but for which there is no proof that it is both always fast and always produces a good result.Metaheuristicapproaches are often used.
One example of a heuristic algorithm is a suboptimalgreedy coloring algorithmused forgraph coloringduring theregister allocationphase of some compilers, a technique calledgraph-coloring global register allocation.Each vertex is a variable, edges are drawn between variables which are being used at the same time, and colors indicate the register assigned to each variable. Because mostRISCmachines have a fairly large number of general-purpose registers, even a heuristic approach is effective for this application.
Completeness under different types of reduction
[edit]In the definition of NP-complete given above, the termreductionwas used in the technical meaning of a polynomial-timemany-one reduction.
Another type of reduction is polynomial-timeTuring reduction.A problemis polynomial-time Turing-reducible to a problemif, given a subroutine that solvesin polynomial time, one could write a program that calls this subroutine and solvesin polynomial time. This contrasts with many-one reducibility, which has the restriction that the program can only call the subroutine once, and the return value of the subroutine must be the return value of the program.
If one defines the analogue to NP-complete with Turing reductions instead of many-one reductions, the resulting set of problems won't be smaller than NP-complete; it is an open question whether it will be any larger.
Another type of reduction that is also often used to define NP-completeness is thelogarithmic-space many-one reductionwhich is a many-one reduction that can be computed with only a logarithmic amount of space. Since every computation that can be done inlogarithmic spacecan also be done in polynomial time it follows that if there is a logarithmic-space many-one reduction then there is also a polynomial-time many-one reduction. This type of reduction is more refined than the more usual polynomial-time many-one reductions and it allows us to distinguish more classes such asP-complete.Whether under these types of reductions the definition of NP-complete changes is still an open problem. All currently known NP-complete problems are NP-complete under log space reductions. All currently known NP-complete problems remain NP-complete even under much weaker reductions such asreductions andreductions. Some NP-Complete problems such as SAT are known to be complete even under polylogarithmic time projections.[7]It is known, however, thatAC0reductions define a strictly smaller class than polynomial-time reductions.[8]
Naming
[edit]According toDonald Knuth,the name "NP-complete" was popularized byAlfred Aho,John HopcroftandJeffrey Ullmanin their celebrated textbook "The Design and Analysis of Computer Algorithms". He reports that they introduced the change in thegalley proofsfor the book (from "polynomially-complete" ), in accordance with the results of a poll he had conducted of thetheoretical computer sciencecommunity.[9]Other suggestions made in the poll[10]included "Herculean","formidable ",Steiglitz's "hard-boiled" in honor of Cook, and Shen Lin's acronym "PET", which stood for "probably exponential time", but depending on which way theP versus NP problemwent, could stand for "provably exponential time" or "previously exponential time".[11]
Common misconceptions
[edit]The following misconceptions are frequent.[12]
- "NP-complete problems are the most difficult known problems."Since NP-complete problems are in NP, their running time is at most exponential. However, some problems have been proven to require more time, for examplePresburger arithmetic.Of some problems, it has even been proven that they can never be solved at all, for example thehalting problem.
- "NP-complete problems are difficult because there are so many different solutions."On the one hand, there are many problems that have a solution space just as large, but can be solved in polynomial time (for exampleminimum spanning tree). On the other hand, there are NP-problems with at most one solution that are NP-hard under randomized polynomial-time reduction (seeValiant–Vazirani theorem).
- "Solving NP-complete problems requires exponential time."First, this would imply P ≠ NP, which is still an unsolved question. Further, some NP-complete problems actually have algorithms running in superpolynomial, but subexponential time such as O(2√nn). For example, theindependent setanddominating setproblems forplanar graphsare NP-complete, but can be solved in subexponential time using theplanar separator theorem.[13]
- "Each instance of an NP-complete problem is difficult."Often some instances, or even most instances, may be easy to solve within polynomial time. However, unless P=NP, any polynomial-time algorithm must asymptotically be wrong on more than polynomially many of the exponentially many inputs of a certain size.[14]
- "If P=NP, all cryptographic ciphers can be broken."A polynomial-time problem can be very difficult to solve in practice if the polynomial's degree or constants are large enough. In addition,information-theoretic securityprovides cryptographic methods that cannot be broken even with unlimited computing power.
- "A large-scale quantum computer would be able to efficiently solve NP-complete problems."The class of decision problems that can be efficiently solved (in principle) by a fault-tolerant quantum computer is known as BQP. However, BQP is not believed to contain all of NP, and if it does not, then it cannot contain any NP-complete problem.[15]
Properties
[edit]Viewing adecision problemas a formal language in some fixed encoding, the set NPC of all NP-complete problems isnot closedunder:
It is not known whether NPC is closed undercomplementation,since NPC=co-NPCif and only if NP=co-NP,and since NP=co-NP is anopen question.[16]
See also
[edit]- Almost complete
- Gadget (computer science)
- Ladner's theorem
- List of NP-complete problems
- NP-hard
- P = NP problem
- Strongly NP-complete
- Travelling Salesman (2012 film)
References
[edit]Citations
[edit]- ^For example, simply assigningtrueto each variable renders the 18th conjunct(and hence the complete formula)false.
- ^Cobham, Alan(1965). "The intrinsic computational difficulty of functions".Proc. Logic, Methodology, and Philosophy of Science II.North Holland.
- ^J. van Leeuwen (1998).Handbook of Theoretical Computer Science.Elsevier. p. 84.ISBN978-0-262-72014-4.
- ^J. van Leeuwen (1998).Handbook of Theoretical Computer Science.Elsevier. p. 80.ISBN978-0-262-72014-4.
- ^Kiersz, Andy."An eminent mathematician claims to have solved one of math's greatest mysteries — and it's one of 6 problems with a $1 million prize".Business Insider.Retrieved2023-04-24.
- ^Chen, Jianer; Kanj, Iyad A.; Xia, Ge (2010-09-06)."Improved upper bounds for vertex cover".Theoretical Computer Science.411(40): 3736–3756.doi:10.1016/j.tcs.2010.06.026.ISSN0304-3975.
- ^Agrawal, M.;Allender, E.;Rudich, Steven(1998)."Reductions in Circuit Complexity: An Isomorphism Theorem and a Gap Theorem".Journal of Computer and System Sciences.57(2): 127–143.doi:10.1006/jcss.1998.1583.ISSN1090-2724.
- ^Agrawal, M.;Allender, E.; Impagliazzo, R.;Pitassi, T.;Rudich, Steven(2001). "Reducing the complexity of reductions".Computational Complexity.10(2): 117–138.doi:10.1007/s00037-001-8191-1.ISSN1016-3328.S2CID29017219.
- ^Don Knuth,Tracy Larrabee, and Paul M. Roberts,Mathematical WritingArchived2010-08-27 at theWayback Machine§ 25,MAA Notes No. 14,MAA, 1989 (alsoStanfordTechnical Report, 1987).
- ^Knuth, D. F. (1974). "A terminological proposal".SIGACT News.6(1): 12–18.doi:10.1145/1811129.1811130.S2CID45313676.
- ^See the poll, or[1]Archived2011-06-07 at theWayback Machine.
- ^Ball, Philip (2000)."DNA computer helps travelling salesman".Nature.doi:10.1038/news000113-10.
- ^Bern (1990);Deĭneko, Klinz & Woeginger (2006);Dorn et al. (2005);Lipton & Tarjan (1980).
- ^Hemaspaandra, L. A.; Williams, R. (2012). "SIGACT News Complexity Theory Column 76".ACM SIGACT News.43(4): 70.doi:10.1145/2421119.2421135.S2CID13367514.
- ^Aaronson, Scott (2010). "BQP and the polynomial hierarchy". In Schulman, Leonard J. (ed.).Proceedings of the 42nd ACM Symposium on Theory of Computing, STOC 2010, Cambridge, Massachusetts, USA, 5–8 June 2010.Association for Computing Machinery. pp. 141–150.arXiv:0910.4698.doi:10.1145/1806689.1806711.ISBN978-1-4503-0050-6.
- ^Talbot, John;Welsh, D. J. A.(2006),Complexity and Cryptography: An Introduction,Cambridge University Press, p. 57,ISBN9780521617710,
The question of whether NP and co-NP are equal is probably the second most important open problem in complexity theory, after the P versus NP question.
Sources
[edit]- Garey, Michael R.;Johnson, David S.(1979).Computers and Intractability: A Guide to the Theory of NP-Completeness.Series of Books in the Mathematical Sciences (1st ed.). New York:W. H. Freeman and Company.ISBN9780716710455.MR0519066.OCLC247570676.This book is a classic, developing the theory, then cataloguingmanyNP-Complete problems.
- Cook, S.A.(1971). "The complexity of theorem proving procedures".Proceedings, Third Annual ACM Symposium on the Theory of Computing, ACM, New York.pp. 151–158.doi:10.1145/800157.805047.
- Dunne, P.E."An annotated list of selected NP-complete problems".COMP202, Dept. of Computer Science,University of Liverpool.Retrieved2008-06-21.
- Crescenzi, P.; Kann, V.; Halldórsson, M.;Karpinski, M.;Woeginger, G."A compendium of NP optimization problems".KTH, Stockholm.Retrieved2020-10-24.
- Dahlke, K."NP-complete problems".Math Reference Project.Retrieved2008-06-21.
- Karlsson, R."Lecture 8: NP-complete problems"(PDF).Dept. of Computer Science, Lund University, Sweden. Archived fromthe original(PDF)on April 19, 2009.Retrieved2008-06-21.
- Sun, H.M."The theory of NP-completeness".Information Security Laboratory, Dept. of Computer Science,National Tsing Hua University,Hsinchu City, Taiwan. Archived fromthe original(PPT)on 2009-09-02.Retrieved2008-06-21.
- Jiang, J.R."The theory of NP-completeness"(PPT).Dept. of Computer Science and Information Engineering,National Central University,Jhongli City, Taiwan.Retrieved2008-06-21.
- Cormen, T.H.;Leiserson, C.E.;Rivest, R.L.;Stein, C.(2001). "Chapter 34: NP–Completeness".Introduction to Algorithms(2nd ed.). MIT Press and McGraw-Hill. pp. 966–1021.ISBN978-0-262-03293-3.
- Sipser, M.(1997)."Sections 7.4–7.5 (NP-completeness, Additional NP-complete Problems)".Introduction to the Theory of Computation.PWS Publishing. pp.248–271.ISBN978-0-534-94728-6.
- Papadimitriou, C.(1994). "Chapter 9 (NP-complete problems)".Computational Complexity(1st ed.). Addison Wesley. pp. 181–218.ISBN978-0-201-53082-7.
- Computational Complexity of Games and Puzzles
- Tetris is Hard, Even to Approximate
- Minesweeper is NP-complete!
- Bern, Marshall (1990). "Faster exact algorithms for Steiner trees in planar networks".Networks.20(1): 109–120.doi:10.1002/net.3230200110..
- Deĭneko, Vladimir G.; Klinz, Bettina;Woeginger, Gerhard J.(2006). "Exact algorithms for the Hamiltonian cycle problem in planar graphs".Operations Research Letters.34(3): 269–274.doi:10.1016/j.orl.2005.04.013..
- Dorn, Frederic; Penninkx, Eelko;Bodlaender, Hans L.;Fomin, Fedor V. (2005). "Efficient Exact Algorithms on Planar Graphs: Exploiting Sphere Cut Branch Decompositions".Proc. 13th European Symposium on Algorithms (ESA '05).Lecture Notes in Computer Science. Vol. 3669. Springer-Verlag. pp. 95–106.doi:10.1007/11561071_11.ISBN978-3-540-29118-3..
- Lipton, Richard J.;Tarjan, Robert E.(1980). "Applications of a planar separator theorem".SIAM Journal on Computing.9(3): 615–627.doi:10.1137/0209046.S2CID12961628..
Further reading
[edit]- Scott Aaronson,NP-complete Problems and Physical Reality,ACMSIGACTNews, Vol. 36, No. 1. (March 2005), pp. 30–52.
- Lance Fortnow,The status of the P versus NP problem,Commun. ACM,Vol. 52, No. 9. (2009), pp. 78–86.









